מחקר על ה-Augmented Dickey-Fuller (ADF) מבחן מדוגמה מוזרה
נייחות היא אחד המושגים הבסיסיים ביותר לניתוח סדרות זמן. באופן כללי, נייחות תספק מאפיינים מצוינים למידול סדרות הזמן בשיטות סטטיסטיות שונות. Augmented Dickey-Fuller (ADF) בדיקה היא כנראה הגישה הנפוצה ביותר לבדיקת נייחות.
יש טונות של מאמרים באינטרנט בנושא זה. אני לא אבזבז את זמנכם על המבוא הבסיסי, כמו הגדרת נייחות, איך עושים בדיקות ADF וכו'. בפוסט הזה אשתף את המסע שלי לחקור את מבחן ה-ADF לאחר שנתקלתי במקרה מוזר באפליקציה.
מסלול הלמידה שאראה אופייני ללימוד מדעי הנתונים. ראשית, אנחנו חושבים שאנחנו מבינים כלי או מושג, אבל אנחנו פשוט מכירים וזוכרים את המונח. כאשר אנו מיישמים אותו על נתונים ממשיים, אנו עשויים למצוא בעיות בלתי צפויות ומאתגרות שדוחפות אותנו לחקור יותר ולהבין יותר.
שוב, אני אחלוק את הקוד שלי ב-GitHub; אנא מצא את הקישור בסעיף ההפניה סוף סוף.
תחילתו של מסע בלתי צפוי
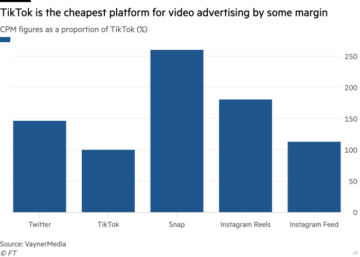
עבדתי עם כמה סדרות זמן לפני כמה ימים. איור 1 מציג אחד מהם. אין כפל א מגמת עלייה קיימת, ו השונות גם משתנה עם הזמן. עם ההדמיה הברורה הזו, לא הייתי צריך לבדוק את הנייחות. מסיבה כלשהי שאני לא זוכר, עדיין ניסיתי את זה עם בדיקת ADF. באופן מפתיע, ערך ה-p הוא כמעט 0, מה שמרמז שעלי לדחות את השערת האפס ולקבל אותה שהיא נייחת.
זה מוזר. תוצאת הבדיקה נראתה שגויה. רציתי לחקור מה קורה מאחורי בדיקת ה-ADF. הצעד הראשון שניסיתי היה לשכפל את הבעיה הזו עם נתונים סינתטיים. יצרתי כמה נתוני בדיקה עם הקוד הבא. הקוד רק חיקה את ההתנהגות של מגמות איטיות אבל לא את העונתיות.
יש 20,000 תצפיות באיור 1, מה שמרמז שהמגמה עולה לאט ביותר. אני יוצר סדרת זמן עם שיפוע קטן של 0.0005. הערך הממוצע של סדרת הזמן עולה מסביבות 0 ל-0.5 לאחר 1000 תצפיות. אז בואו נבדוק את זה עם הפונקציה adfuller() מ statsmodels.tsa.stattools עם פרמטרי ברירת המחדל. ערך p הוא 0.01, וה"בעיה" מתרחשת שוב. איור 2 מציג את התוצאה. אתה יכול להתעלם מהכותרת, ולהתמקד במגמת העלייה. אסביר מדוע יש לנו ערכי p משלוש בדיקות ADF שונות מאוחר יותר.
המתמטיקה מאחורי מבחן DF
עלינו לרדת לעומק כדי לראות מה בדיוק עושה בדיקת ה-ADF. מסתבר שהרקע המתמטי שלו לא מסובך. ראשית, מבחן ה-ADF הוא רק גרסה מתקדמת של מבחן דיקי-פולר. יש שלוש גרסאות עיקריות של מבחן DF (מתוך ויקיפדיה):
הגרסה 1: בדיקה עבור שורש יחידה: ∆yᵢ = δyᵢ₋₁ + uᵢ
הגרסה 2: בדוק שורש יחידה עם קבוע: ∆yᵢ = a₀ + δyᵢ₋₁ + uᵢ
הגרסה 3. בדיקת שורש יחידה עם מגמה קבועה ודטרמיניסטית: ∆yᵢ = a₀ + a₁*t + δyᵢ₋₁ + uᵢ
בכל גרסה, השערת האפס היא שיש שורש יחידה, δ=0.
חבילת Statsmodels תומכת בכל שלוש הגרסאות עם הפרמטר "נְסִיגָה".
עבור גרסה 1, הרגרסיה היא 'n' (ללא קבוע, אין מגמה).
עבור גרסה 2, הרגרסיה היא 'c' (קבוע בלבד); זוהי הגדרת ברירת המחדל.
עבור גרסה 3, רגרסיה היא 'ct' (קבוע ומגמה).
אני מריץ את הבדיקה מחדש עם שלוש הגדרות שונות, ולהלן התוצאות החדשות.
עבור גרסה 1, ערך ה-p הוא 0.09. אל לנו לדחות את השערת האפס.
עבור גרסה 2, ערך ה-p הוא 0.01. כבר התייחסנו לזה כבעיה כי זו הגדרת ברירת המחדל.
עבור גרסה 3, ערך ה-p הוא 0.00. זה צפוי כי סדרת הזמן היא אכן נייח עם מגמה דטרמיניסטית.
אז לגבי הנתונים לדוגמה האלה, אם נבדוק אותם עם גרסה 1 (רגרסיה='n'), לא נגיד שהם נייחים. אנחנו כנראה לא צריכים להשתמש בהגדרת ברירת המחדל. אבל אתם עשויים גם לתהות, מדוע המונח הקבוע עשה כאן הבדל כה גדול? בואו נחפור יותר.
ממבחן DF לרגרסיה לינארית
בהתבסס על ההגדרה לעיל, מבחן DF הוא רק רגרסיה ליניארית. איור 3 מציג את כל הנקודות עבור הרגרסיה הליניארית. ציר Y הוא ∆yᵢ, ציר X הוא yᵢ₋₁, ו-uᵢ הוא השארית. גרסה 1 פירושה שעלינו להתאים קו ללא יירוט (ללא קבוע). גרסה 2 פירושה שעלינו להתאים קו עם יירוט (קבוע).
Skitlearn LinearRegression תומך היטב בשתי האפשרויות הללו עם הפרמטר fit_intercept. מתחת לאיור 4 מופיעים שני הקווים המותאמים. כפי שאתה יכול לראות, הקו עם המיירט מתאים יותר מהקו בלי המיירט. גם הציון בריבוע R אישר זאת בבירור. כמו כן, שימו לב שהשיפוע של הקו הכתום קטן מזה של הקו הכחול. במילים אחרות, השיפוע של הקו הכתום קרוב יותר ל-0.
אנו יכולים לחשוב גם באמצעות הדמיה: הנקודות אינן ממורכזות סביב (0,0), כך שקו הרגרסיה המותאם לא אמור לעבור (0,0). החיתוך צריך להיות גדול מ-0. מכיוון ש-0 הוא הממוצע ההתחלתי, ∆y צריך להיות גדול מ-0, אז הממוצע הכולל יגדל. אם נאלץ את קו הרגרסיה לעבור (0,0), הוא יתאים לנתונים, והשיפוע יתקרב ל-0 בגלל ההשפעה של (0,0).
ראינו אם הכללת השפעות היירוט מתאימה לרגרסיה הליניארית. מדוע אופן התאמת הקו משפיע על תוצאות בדיקת ADF, ומאיפה מגיע ערך ה-p?
מרגרסיה לינארית ל-p-value
עכשיו זה המקום שמסתבך קצת. ערך ה-p הסופי של מבחן DF אינו מערך ה-p של המקדמים מהרגרסיה הליניארית. בעיקרון, לסטטיסטיקה יש התפלגות ספציפית המכונה טבלת Dickey-Fuller. לאחר מכן אנו משתמשים בערך ה-p המשוער של מקינון עבור סטטיסטיקת הבדיקה. ייתכן שתמצא את הפרטים ב- קוד המקור של Statsmodels.
מכיוון שהשערת האפס היא δ=0, כלומר בדיקת השיפוע של הקו המותאם היא 0. אין לנו צורך להיכנס לפרטים כיצד לקבל את ערך ה-p. השרשרת הלוגית של הקשר בין ערך ה-p לבין השיפוע (δ ברגרסיה ליניארית, לא השיפוע המגמתי) היא כזו:
בדרך כלל, אם השיפוע רחוק מ-0, ערך ה-p צריך להיות קטן יותר, סביר יותר לדחות את השערת האפס ולא להציע שורש יחידה ונייח. אם השיפוע הוא 0 או קרוב מאוד ל-0, ערך ה-p צריך להיות גבוה יותר, סביר יותר לקבל את השערת האפס ולהציע שורש יחידה ולא נייח. עבור התרחיש השני, ויקיפדיה אומרת, "לבדיקות יש כוח סטטיסטי נמוך בכך שלעתים קרובות הם לא יכולים להבחין בין תהליכים אמיתיים של יחידת שורש (δ = 0) לבין תהליכים קרובים ליחידה-שורש (δ קרוב ל-0)". לכן יש לנו את הבעיה מלכתחילה. אנו מתמודדים עם תהליך קרוב ליחידה-שורש. גרסה 1 מוצאת שורש יחידה וגרסה 2 לא יכולה למצוא שורש יחידה.
מדוע גרסה 1 עובדת עבור הדוגמה לעיל?
גרסה 1 עובדת עבור נתונים באיור 2 מכיוון שאנו מקרובים את השיפוע ל-0, כך שערך ה-p גבוה יותר.
עם זאת, איננו יכולים להשתמש בגרסה 1 כהגדרת ברירת המחדל. ישנם שני מקרים עבור גרסה 1 (הכריח את הקו לעבור (0,0)):
מקרה 1: (0,0) קרוב יותר לכל נקודות הנתונים. אם הקו צריך לעבור (0,0), אז הקו יהיה שטוח יותר, והשיפוע יתקרב ל-0. איור 4 מדגים את המקרה הזה. שימו לב שההדגמה באיור 4 מתאימה רק למשתנה אחד yᵢ₋₁, ה-ADF בפועל יתאים למשתני פיגור נוספים.
מקרה 2: (0,0) רחוק מכל נקודות הנתונים. אם הקו חייב לעבור (0,0), אנו עלולים להיכשל בהתאמה; למעשה, השיפוע הוא 0, כלומר איננו יכולים למצוא קשר ליניארי של ∆yᵢ ו-yᵢ₋₁ כך שקו יעבור (0,0) ויכסה את רוב נקודות הנתונים. לכן, תוצאת הבדיקה תהיה מוטה ליחידת שורש.
איור 5 להלן מציג דוגמה של מבחן גרסה 1 שלא הצליח לדחות את השערת האפס (p-value 0.6), והנתונים הם נייחים עם ממוצע של 10. איור 6 מסביר את הסיבה. כפי שאתה יכול לראות, איננו יכולים למצוא קו ללא יירוט (R-ריבוע הוא 0), ולכן השיפוע של הקו המותאם הוא 0 (∆yᵢ אינו תלוי ב-yᵢ₋₁).
מבדיקת DF למבחן ADF
כעת הבנו שמבחן ה-DF הוא רגרסיה ליניארית וכיצד לקבל את ערך ה-p מהרגרסיה הליניארית, נעבור ל-ADF. הנוסחה של ADF היא:
שוב, רגרסיה לינארית. החלק "המורחב" הוא שעלינו להתאים יותר מקדמים.
חבילת statsmodels מאפשרת הצגת סיכום מפורט של מבחן AFT. איור 7 הוא התוצאה.
אנו רואים 'OLS Regression' (פתרון ברירת המחדל עבור רגרסיה ליניארית) ו-17 מקדמים. לא ציינתי את ההשהיה המקסימלית, אז הבדיקה תנסה עד למספר המבוסס על אורך סדרת הזמן, שהוא 17.
ה-const (מיירט) מותקן גם כן. הערך הוא 0.0596.
בואו ננסה ליישם את מבחן ה-ADF באמצעות רגרסיה לינארית ב-Skikit-learn. איור 8 הוא הקוד והפלט.
החיתוך הוא 0.0596, והמקדמים האחרים זהים לתמונה 7. הרגרסיה הליניארית ב-Skikit-learn היא פשוט OLS. אנחנו עושים את אותו הדבר, אז זה לא מפתיע שהתוצאות זהות.
סוף המסע
לאחר שהבנתי כיצד להגדיר את הפרמטר, בדקתי את סדרת הזמן המקורית באיור 1 באמצעות גרסה 1 (רגרסיה ='n') וקיבלתי את ערך ה-p של 0.08, מה שמרמז על כך שהוא לא נייח. שימו לב שהנתונים באיור 1 הם אפס-ממוצע, כך שאתם יכולים לדמיין ש-(0,0) קרוב יותר לנקודות הנתונים (∆yᵢ, yᵢ₋₁). שימוש במבחן גרסה 1 יעזור לנו.
מכיוון שהשיפוע המגמתי באיור 1 הוא מינימלי, אנו יכולים גם לדגום מחדש את סדרת הזמן עם צעדים, מה שמגדיל את השיפוע. לדוגמה, אם אני בודק אותו בארבעה שלבים (ערך[::4] ), הוא לא יעבור את מבחן ה-ADF עם הגדרת ברירת המחדל (p-value הוא 0.17 עבור רגרסיה='c').
הבעיה נפתרה.
Takeaways
אל תסמוך על תוצאות ADF באופן עיוור. הדמיה היא החבר שלך.
מבחן ADF הוא רגרסיה ליניארית פשוטה, והיישום של מודלים סטטיסטיים משתמש ב-OLS כדי לפתור את בעיית הרגרסיה. לאחר מכן הוא משתמש בטבלה Dickey–Fuller כדי לחלץ את ערך ה-p אשר מאמת את השערת ה-Null לפיה המקדם של משתנה הפיגור הראשון מהרגרסיה המותאמת הוא 0.
לבדיקת ADF יש מגבלות בעת בדיקת התהליכים הקרובים ליחידה-שורש (δ קרוב ל-0).
אנחנו צריכים לבחור את גרסת ה-ADF המתאימה בהתאם. לדוגמה, כאשר אתה רואה מגמה קבועה וברצונך לבדוק 'טרנד נייח', עליך לבחור 'ct' כפרמטר. אם אתה מתכוון לתפוס מגמה איטית עבור אות שהממוצע שלו אמור להיות 0 כמו באיור 1 ואיור 2, אולי אתה צריך לבחור 'n' כפרמטר כדי למנוע את ההשפעה של התאמת המיירט. Statsmodels תומכים גם במגמה קוונטית עם הפרמטר 'ctt'. אפשרות מתקדמת זו יכולה להיות בחירה טובה עבור מקרים מסוימים. במקרה שאתה רוצה לחפור יותר, אנא עיין ב התמודדות עם חוסר ודאות לגבי הכללת המונחים של יירוט ומגמת זמן דטרמיניסטית.
אני מקווה שלמדת משהו על מבחן ADF.
תהנה עם סדרת הזמן שלך!
צרו איתי קשר ב לינקדין.
נ.ב.: יש לי ניסיון ותשוקה לנתוני סדרות זמן. אם אתה אוהב את המאמר הזה, אתה עשוי להתעניין באחר שלי פוסטים על סדרות זמן.
הפניות
מדוע סדרת הזמן המגמתית הזו נייחת? פורסם מחדש ממקור https://towardsdatascience.com/why-is-this-trending-time-series-stationary-f3fb9447336f?source=rss—-7f60cf5620c9—4 דרך https://towardsdatascience.com/feed
<!–
->