체비쇼프 보간법을 사용하여 트로터 시뮬레이션의 정확도 향상

체비쇼프 보간법을 사용하여 트로터 시뮬레이션의 정확도 향상

타임 스탬프 : 26 년 2024 월 9 일 오전 34:XNUMX

구마로 렌돈1, 제이콥 왓킨스2및 Nathan Wiebe3,4

1Zapata Computing Inc., 보스턴, MA 02110, 미국
2희귀 동위원소 빔 시설, 미시간 주립대학교, East Lansing, MI 48824, USA
3토론토 대학교 컴퓨터 과학부, 토론토, ON M5S 2E4, 캐나다
4미국 WA 99352 리치 랜드 Pacific Northwest National Laboratory

이 논문이 흥미 롭거나 토론하고 싶습니까? SciRate에 댓글을 달거나 댓글 남기기.

추상

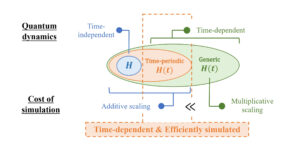
양자 계측법을 사용하면 최적의 하이젠베르그 한계에서 양자 시스템의 특성을 측정할 수 있습니다. 그러나 관련 양자 상태가 디지털 해밀턴 시뮬레이션을 사용하여 준비되면 발생하는 알고리즘 오류로 인해 이 근본적인 한계에서 벗어나게 됩니다. 이 연구에서는 표준 다항식 보간 기술을 사용하여 Trotterized 시간 진화로 인한 알고리즘 오류를 어떻게 완화할 수 있는지 보여줍니다. 우리의 접근 방식은 하드웨어 오류를 완화하기 위한 제로 노이즈 추정 기술과 유사하게 Trotter 단계 크기를 0으로 추정하는 것입니다. 우리는 고유값과 시간에 따른 기대값을 추정하기 위한 보간법의 엄격한 오류 분석을 수행하고 오류의 다대수 인자까지 하이젠베르그 한계가 달성된다는 것을 보여줍니다. 우리의 작업은 다양한 관련 알고리즘 작업에 Trotter 및 고전 리소스만 사용하여 최첨단 시뮬레이션 알고리즘에 접근하는 정확도를 달성할 수 있음을 시사합니다.

Chebyshev 보간 PlatoBlockchain 데이터 인텔리전스를 사용하여 트로터 시뮬레이션의 정확도가 향상되었습니다. 수직 검색. 일체 포함.

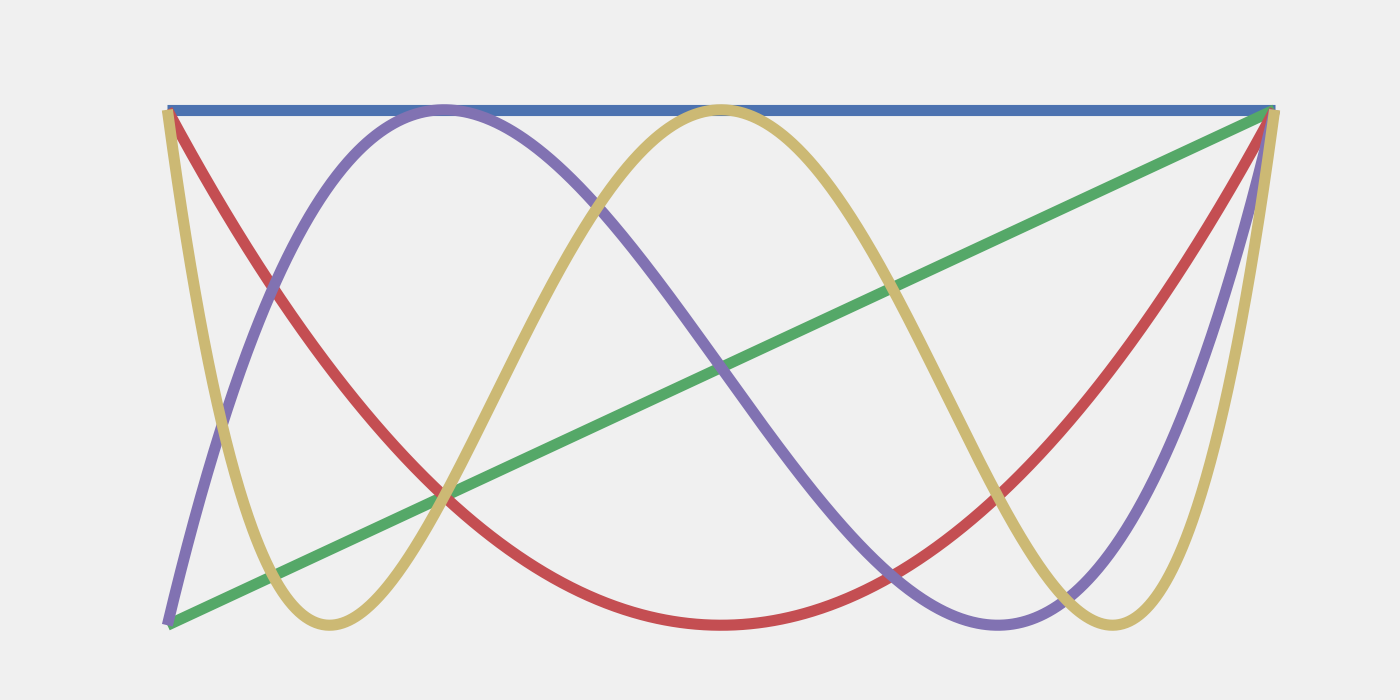
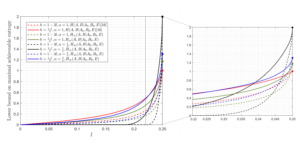
주요 이미지: 처음 5개의 체비쇼프 다항식. 체비쇼프 0에서의 보간은 트로터 오류 완화를 위한 강력한 방식으로 사용됩니다.

[포함 된 콘텐츠]

인기 요약

양자 컴퓨터는 향상된 양자 시뮬레이션을 통해 화학, 재료, 핵물리학 및 기타 과학 분야에 대한 이해를 향상시킬 수 있는 잠재력을 가지고 있습니다. 이 작업에는 여러 가지 사용 가능한 양자 알고리즘이 있으며, 그 중에서 Trotter 공식은 단순성과 낮은 초기 비용으로 인해 선호되는 경우가 많습니다. 불행하게도 Trotter 공식은 이론적으로 더 새롭고 정교한 경쟁사에 비해 상대적으로 부정확합니다. 더 많은 계산 시간이 도움이 될 수 있지만, 이 전략은 길고 중단 없는 계산을 수행하는 능력이 제한되어 오늘날의 시끄러운 양자 장치에서는 빠르게 관리할 수 없게 됩니다.

양자 처리 시간을 늘리지 않고 Trotter 시뮬레이션의 오류를 완화하기 위해 다항식을 사용하여 오류와 단계 크기 간의 관계를 학습합니다. 다양한 단계 크기 선택에 대한 데이터를 수집함으로써 다항식을 사용하여 데이터를 보간(예: 스레드)한 다음 매우 작은 단계 크기에 대해 예상되는 동작을 추정할 수 있습니다. 우리는 우리의 접근 방식이 고유값 추정과 기대값 추정이라는 두 가지 기본 작업에 대해 표준 Trotter에 비해 점근적 정확도 향상을 가져온다는 것을 수학적으로 증명합니다.

우리의 방법은 간단하고 실용적이며 양자 및 고전 계산에서 표준 기술만 필요합니다. 우리는 우리의 연구가 알고리즘 오류 완화에 대한 추가 조사를 위한 강력한 이론적 기반을 제공한다고 믿습니다. 이 작업의 확장은 분석에서 인위적인 가정을 제거하는 것부터 향상된 양자 시뮬레이션을 시연하는 것까지 여러 방향으로 발생할 수 있습니다.

► BibTeX 데이터

► 참고 문헌

[1] S. Lloyd, Universal 양자 시뮬레이터, Science 273 (1996) 1073.
https : / /doi.org/10.1126/ science.273.5278.1073

[2] M. Reiher, N. Wiebe, KM Svore, D. Wecker 및 M. Troyer, 양자 컴퓨터의 반응 메커니즘 설명, Proceedings of the National Academy of Sciences 114(2017) 7555.
https : / /doi.org/ 10.1073 / pnas.161915211

[3] JD Whitfield, J. Biamonte 및 A. Aspuru-Guzik, 양자 컴퓨터를 사용한 전자 구조 해밀턴 시뮬레이션, 분자 물리학 109(2011) 735.
https : / /doi.org/ 10.1080 / 00268976.2011.552441

[4] J. Lee, DW Berry, C. Gidney, WJ Huggins, JR McClean, N. Wiebe et al., 텐서 초수축을 통한 화학의 더욱 효율적인 양자 계산, PRX Quantum 2(2021) 030305.
https : / / doi.org/ 10.1103 / PRXQuantum.2.030305

[5] V. von Burg, GH Low, T. Häner, DS Steiger, M. Reiher, M. Roetteler 등, 양자 컴퓨팅 강화된 계산 촉매작용, Physical Review Research 3(2021) 033055.
https : / /doi.org/10.1103/ PhysRevResearch.3.033055

[6] SP Jordan, KS Lee 및 J. Preskill, 양자 장 이론을 위한 양자 알고리즘, Science 336 (2012) 1130.
https : / /doi.org/10.1126/ science.1217069

[7] AF Shaw, P. Lougovski, JR Stryker 및 N. Wiebe, 격자 슈윙거 모델 시뮬레이션을 위한 양자 알고리즘, Quantum 4(2020) 306.
https:/​/​doi.org/​10.22331/​q-2020-08-10-306

[8] N. Klco, MJ Savage 및 JR Stryker, Su (2) 디지털 양자 컴퓨터의 101차원 비아벨 게이지 필드 이론, Physical Review D 2020 (074512) XNUMX.
https : / /doi.org/10.1103/PhysRevD.101.074512

[9] AM Childs 및 N. Wiebe, 단일 연산의 선형 조합을 사용한 해밀턴 시뮬레이션, Quantum Info. 계산. 12 (2012) 901-924.
https : / / doi.org/ 10.26421 / QIC12.11-12-1

[10] GH Low, V. Kliuchnikov 및 N. Wiebe, 조건이 좋은 다중곱물 해밀턴 시뮬레이션, arXiv:1907.11679 (2019).
https://​/​doi.org/​10.48550/​arXiv.1907.11679
arXiv : 1907.11679

[11] DW Berry, AM Childs, R. Cleve, R. Kothari 및 RD Somma, 잘린 테일러 시리즈를 사용한 해밀턴 동역학 시뮬레이션, 물리적 검토 편지 114(2015) 090502.
https : / /doi.org/10.1103/ PhysRevLett.114.090502

[12] GH Low 및 N. Wiebe, 상호 작용 사진의 해밀턴 시뮬레이션, arXiv:1805.00675(2018).
https://​/​doi.org/​10.48550/​arXiv.1805.00675
arXiv : 1805.00675

[13] M. Kieferová, A. Scherer 및 DW Berry, 잘린 다이슨 시리즈를 사용하여 시간 종속 해밀턴의 역학 시뮬레이션, Physical Review A 99 (2019) 042314.
https : / /doi.org/10.1103/ PhysRevA.99.042314

[14] GH Low 및 IL Chuang, Qubitization을 통한 해밀턴 시뮬레이션, Quantum 3(2019) 163.
https:/​/​doi.org/​10.22331/​q-2019-07-12-163

[15] R. Babbush, C. Gidney, DW Berry, N. Wiebe, J. McClean, A. Paler 등, 선형 t 복잡도를 갖는 양자 회로의 전자 스펙트럼 인코딩, 물리적 검토 X 8(2018) 041015.
https : / /doi.org/10.1103/ PhysRevX.8.041015

[16] DW Berry, G. Ahokas, R. Cleve 및 BC Sanders, 희소 해밀턴 시뮬레이션을 위한 효율적인 양자 알고리즘, Communications in Mathematical Physics 270 (2006) 359-371.
https : / /doi.org/ 10.1007 / s00220-006-0150-x

[17] N. Wiebe, DW Berry, P. Høyer 및 BC Sanders, 양자 컴퓨터에서 양자 역학 시뮬레이션, Journal of Physics A: Mathematical and Theoretical 44 (2011) 445308.
https:/​/​doi.org/​10.1088/​1751-8113/​44/​44/​445308

[18] AM Childs, Y. Su, MC Tran, N. Wiebe 및 S. Zhu, 정류자 스케일링을 사용한 족보 오차 이론, Physical Review X 11(2021) 011020.
https : / /doi.org/10.1103/ PhysRevX.11.011020

[19] J. Haah, MB Hastings, R. Kothari 및 GH Low, 격자 해밀토니안의 실시간 진화 시뮬레이션을 위한 양자 알고리즘, SIAM Journal on Computing(2021) FOCS18.
https : / //doi.org/10.1137/ 18M12315

[20] M. Hagan 및 N. Wiebe, 복합 양자 시뮬레이션, arXiv:2206.06409(2022).
https:/​/​doi.org/​10.22331/​q-2023-11-14-1181
arXiv : 2206.06409

[21] GH Low, Y. Su, Y. Tong 및 MC Tran, 족보 단계 구현의 복잡성에 대해, arXiv:2211.09133(2022).
https : / / doi.org/ 10.1103 / PRXQuantum.4.020323
arXiv : 2211.09133

[22] GH Low 및 IL Chuang, 양자 신호 처리를 통한 최적의 해밀턴 시뮬레이션, Physical Review Letters 118(2017).
https : / //doi.org/10.1103/ physrevlett.118.010501

[23] S. Endo, Q. Zhao, Y. Li, S. Benjamin 및 X. Yuan, 해밀턴 시뮬레이션에서 알고리즘 오류 완화, Phys. A 99(2019) 012334.
https : / /doi.org/10.1103/ PhysRevA.99.012334

[24] AC Vazquez, R. Hiptmair 및 S. Woerner, Richardson 외삽법을 사용하여 양자 선형 시스템 알고리즘 향상, 양자 컴퓨팅의 ACM 트랜잭션 3(2022).
https : / /doi.org/ 10.1145 / 3490631

[25] AC Vazquez, DJ Egger, D. Ochsner 및 S. Woerner, 하드웨어 친화적인 해밀토니안 시뮬레이션을 위한 조건이 좋은 다중곱 공식, Quantum 7(2023) 1067.
https:/​/​doi.org/​10.22331/​q-2023-07-25-1067

[26] M. Suzuki, 다체 이론 및 통계 물리학에 적용되는 프랙탈 경로 적분의 일반 이론, Journal of Mathematical Physics 32(1991) 400.
https : / /doi.org/ 10.1063 / 1.529425

[27] A. Gilyén, Y. Su, GH Low 및 N. Wiebe, 양자 특이값 변환 및 그 이상: 양자 행렬 산술의 기하급수적 개선, 컴퓨팅 이론에 관한 제51차 ACM SIGACT 심포지엄 진행, pp. 193–204, 2019 , DOI.
https : / /doi.org/ 10.1145 / 3313276.3316366

[28] C. Yi 및 E. Crosson, 양자 시뮬레이션을 위한 제품 공식의 스펙트럼 분석, npj Quantum Information 8(2022) 37.
https : / /doi.org/ 10.1038 / s41534-022-00548-w

[29] A. Quarteroni, R. Sacco 및 F. Saleri, 수치 수학, vol. 37, Springer 과학 및 비즈니스 미디어(2010), 10.1007/​b98885.
https : / //doi.org/ 10.1007 / b98885

[30] F. Piazzon 및 M. Vianello, 마르코프 유사 부등식을 통한 르베그 상수의 안정성 부등식, 근사치 11에 대한 Dolomites 연구 노트(2018).

[31] AP de Camargo, 라그랑주 보간에 대한 뉴턴 공식의 수치적 안정성, Journal of Computational and Applied Mathematics 365 (2020) 112369.
https:// / doi.org/ 10.1016/ j.cam.2019.112369

[32] L. Trefethen, 다항식 보간 및 구적법에 대한 여섯 가지 신화(2011).

[33] W. Gautschi, vandermonde 시스템은 얼마나 (불)안정적입니까? 점근적 및 계산적 분석, 순수 및 응용 수학 강의 노트, pp. 193–210, Marcel Dekker, Inc, 1990.

[34] NJ Higham, 무게 중심 라그랑주 보간의 수치 안정성, IMA Journal of Numerical Analysis 24 (2004) 547.
https:/ / doi.org/ 10.1093/ imanum/ 24.4.547

[35] JC Mason 및 DC Handscomb, Chebyshev 다항식, CRC 프레스(2002), 10.1201/​9781420036114.
https : / /doi.org/ 10.1201 / 9781420036114

[36] G. Rendon, T. Izubuchi 및 Y. Kikuchi, 양자 위상 추정에 대한 코사인 테이퍼링 창의 효과, Physical Review D 106 (2022) 034503.
https : / /doi.org/10.1103/PhysRevD.106.034503

[37] LN Trefethen, 근사 이론 및 근사 실습, 확장판, SIAM(2019), 10.1137/​1.9781611975949.
https : / /doi.org/ 10.1137 / 1.9781611975949

[38] FL Bauer 및 CT Fike, 규범 및 배제 정리, Numer. 수학. 2 (1960) 137-141.
https : / /doi.org/ 10.1007 / BF01386217

[39] S. 블래네스, F. 카사스, J.-A. Oteo 및 J. Ros, 매그너스 확장 및 일부 응용 분야, 물리학 보고서 470(2009) 151.
https : / //doi.org/ 10.1016 / j.physrep.2008.11.001

[40] N. Klco 및 MJ Savage, 양자 컴퓨터에서 국부적인 파동 함수의 최소 얽힘 상태 준비, Physical Review A 102(2020).
https : / /doi.org/10.1103/ physreva.102.012612

[41] JJ García-Ripoll, 다변량 분석을 위한 양자 영감 알고리즘: 보간에서 편미분 방정식까지, Quantum 5(2021) 431.
https:/​/​doi.org/​10.22331/​q-2021-04-15-431

[42] W. Górecki, R. Demkowicz-Dobrzański, HM Wiseman 및 DW Berry, $pi$ 수정된 heisenberg 한계, 물리적 검토 편지 124(2020) 030501.
https : / /doi.org/10.1103/ PhysRevLett.124.030501

[43] D. Grinko, J. Gacon, C. Zoufal 및 S. Woerner, 반복적 양자 진폭 추정, npj Quantum Information 7(2021) 52 [1912.05559].
https:/​/​doi.org/​10.1038/​s41534-021-00379-1
arXiv : 1912.05559

[44] N. Wiebe, D. Berry, P. Høyer 및 BC Sanders, 순서 연산자 지수의 고차 분해, Journal of Physics A: Mathematical and Theoretical 43 (2010) 065203.
https:/​/​doi.org/​10.1088/​1751-8113/​43/​6/​065203

[45] RA Horn 및 CR Johnson, 매트릭스 분석, 캠브리지 대학 출판부(2012), 10.1017/​CBO9780511810817.
https : / /doi.org/ 10.1017 / CBO9780511810817

[46] M. Chiani, D. Dardari 및 MK Simon, 페이딩 채널의 오류 확률 계산을 위한 새로운 지수 범위 및 근사치, IEEE Transactions on Wireless Communications 2(2003) 840.
https://doi.org/ 10.1109/ TWC.2003.814350

[47] JM Borwein 및 PB Borwein, Pi 및 AGM: 분석적 수 이론 및 계산 복잡성에 대한 연구, Wiley-Interscience(1987).

[48] BL Higgins, DW Berry, SD Bartlett, HM Wiseman 및 GJ Pryde, Entanglement-free Heisenberg 제한 위상 추정, Nature 450 (2007) 393.
https : / /doi.org/ 10.1038 / nature06257

[49] RB 그리피스와 C.-S. Niu, 양자 계산을 위한 반고전적 푸리에 변환, 물리적 검토 편지 76(1996) 3228.
https : / /doi.org/10.1103/ PhysRevLett.76.3228

[50] AY Kitaev, 양자 측정 및 아벨 안정기 문제, 퀀트-ph/9511026(1995).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9511026
arXiv : 퀀트 -PH / 9511026

[51] DS Abrams 및 S. Lloyd, 고유값 및 고유벡터 찾기에 기하급수적인 속도 증가를 제공하는 양자 알고리즘, Physical Review Letters 83(1999) 5162.
https : / /doi.org/10.1103/ PhysRevLett.83.5162

[52] J. Watkins, N. Wiebe, A. Roggero 및 D. Lee, 이산 시계 구성을 사용한 시간 종속 해밀턴 시뮬레이션, arXiv:2203.11353(2022).
https://​/​doi.org/​10.48550/​arXiv.2203.11353
arXiv : 2203.11353

[53] TD Ahle, 이항 및 포아송 분포의 원시 모멘트에 대한 선명하고 간단한 경계, 통계 및 확률 편지 182(2022) 109306.
https:/​/​doi.org/​10.1016/​j.spl.2021.109306

[54] T. Rivlin, Chebyshev Polynomials, 수학에 관한 Dover 도서, Dover Publications(2020).

인용

[1] 이학장, “고유값 문제를 위한 양자 기법”, 유럽 ​​물리 저널 A 59 11, 275 (2023).

[2] Tatsuhiko N. Ikeda, Hideki Kono 및 Keisuke Fujii, "Trotter24: 해밀턴 시뮬레이션을 위한 정밀도가 보장된 적응형 단계 크기 Trotterization", arXiv : 2307.05406, (2023).

[3] Hans Hon Sang Chan, Richard Meister, Matthew L. Goh, Bálint Koczor, "알고리즘 그림자 분광법", arXiv : 2212.11036, (2022).

[4] Sergiy Zhuk, Niall Robertson 및 Sergey Bravyi, "해밀턴 시뮬레이션을 위한 트로터 오류 범위 및 동적 다중 곱 공식", arXiv : 2306.12569, (2023).

[5] Zhicheng Zhang, Qisheng Wang 및 Mingsheng Ying, "Hamiltonian 시뮬레이션을 위한 병렬 양자 알고리즘", 퀀텀 8, 1228 (2024).

[6] Lea M. Trenkwalder, Eleanor Scerri, Thomas E. O'Brien 및 Vedran Dunjko, "강화 학습을 통한 곱 공식 해밀턴 시뮬레이션 편집", arXiv : 2311.04285, (2023).

[7] Gumaro Rendon 및 Peter D. Johnson, “저심도 가우스 상태 에너지 추정”, arXiv : 2309.16790, (2023).

[8] Gregory Boyd, "통근 운영자를 통한 LCU의 낮은 오버헤드 병렬화", arXiv : 2312.00696, (2023).

위의 인용은 SAO / NASA ADS (마지막으로 성공적으로 업데이트 됨 2024-02-27 02:40:25). 모든 출판사가 적절하고 완전한 인용 데이터를 제공하지는 않기 때문에 목록이 불완전 할 수 있습니다.

On Crossref의 인용 서비스 인용 작품에 대한 데이터가 없습니다 (최종 시도 2024-02-27 02:40:24).

이 백서는 Quantum에서 Creative Commons Attribution 4.0 International(CC BY 4.0) 특허. 저작권은 저자 또는 기관과 같은 원래 저작권 보유자에게 있습니다.

타임 스탬프 :

더보기 양자 저널