Definitieve gids voor K-Means Clustering met Scikit-Learn

Introductie

K-betekent clustering is een van de meest gebruikte onbewaakte algoritmen voor machine learning die clusters van gegevens vormen op basis van de gelijkenis tussen gegevensinstanties.

In deze handleiding zullen we eerst een eenvoudig voorbeeld bekijken om te begrijpen hoe het K-Means-algoritme werkt voordat we het implementeren met Scikit-Learn. Vervolgens bespreken we hoe we het aantal clusters (K's) in K-Means kunnen bepalen, en behandelen we ook afstandsstatistieken, variantie en K-Means voor- en nadelen.

Motivatie

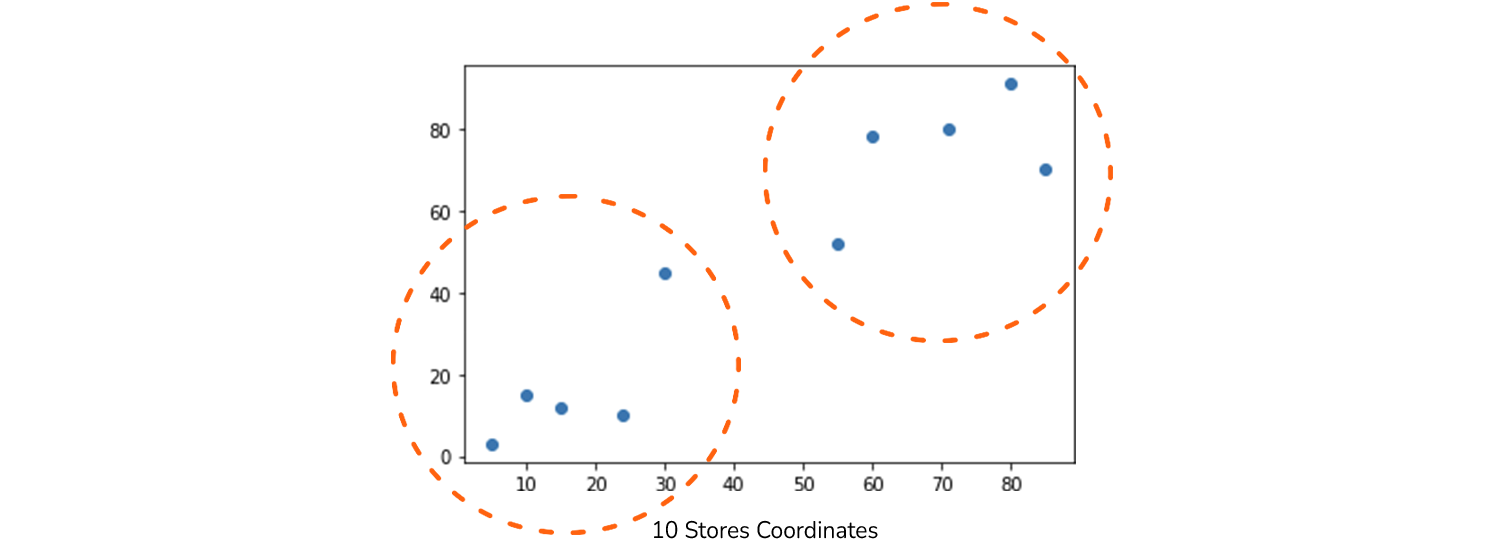
Stel je de volgende situatie voor. Op een dag, toen je door de buurt liep, merkte je dat er 10 buurtwinkels waren en begon je je af te vragen welke winkels vergelijkbaar waren - dichter bij elkaar in de buurt. Tijdens het zoeken naar manieren om die vraag te beantwoorden, kwam je een interessante benadering tegen die de winkels in groepen verdeelt op basis van hun coördinaten op een kaart.

Als een winkel zich bijvoorbeeld 5 km west en 3 km noord zou bevinden, zou u (5, 3) coördineert het en geeft het weer in een grafiek. Laten we dit eerste punt plotten om te visualiseren wat er gebeurt:

import matplotlib.pyplot as plt

plt.title("Store With Coordinates (5, 3)")
plt.scatter(x=5, y=3)

Dit is slechts het eerste punt, zodat we een idee kunnen krijgen van hoe we een winkel kunnen vertegenwoordigen. Stel dat we al 10 coördinaten hebben van de 10 verzamelde winkels. Na ze te hebben georganiseerd in een numpy array, kunnen we ook hun locaties plotten:

import numpy as np

points = np.array([[5, 3], [10, 15], [15, 12], [24, 10], [30, 45], [85, 70], [71, 80], [60, 78], [55, 52],[80, 91]])

xs = points[:,0] 
ys = points[:,1]  

plt.title("10 Stores Coordinates")
plt.scatter(x=xs, y=ys)

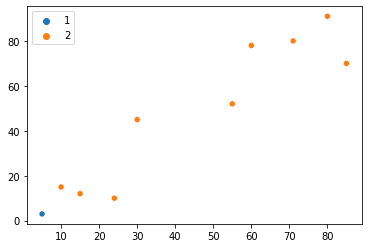
Het K-Means-algoritme handmatig implementeren

Nu kunnen we de 10 winkels in een grafiek bekijken, en het grootste probleem is om te ontdekken of er een manier is om ze in verschillende groepen te verdelen op basis van nabijheid? Gewoon door snel naar de grafiek te kijken, zullen we het waarschijnlijk opmerken twee groepen winkels - de ene is de onderste punten naar linksonder en de andere is de rechterbovenhoek. Misschien kunnen we zelfs die twee punten in het midden als een aparte groep onderscheiden - en zo creëren drie verschillende groepen.

In dit gedeelte bespreken we het proces van het handmatig clusteren van punten - ze verdelen in het opgegeven aantal groepen. Op die manier zullen we in wezen zorgvuldig alle stappen van de K-Means clustering-algoritme. Aan het einde van dit gedeelte krijgt u zowel een intuïtief als praktisch begrip van alle stappen die worden uitgevoerd tijdens de K-Means-clustering. Daarna delegeren we het aan Scikit-Learn.

Wat is de beste manier om te bepalen of er twee of drie groepen punten zijn? Een eenvoudige manier zou zijn om gewoon een aantal groepen te kiezen - bijvoorbeeld twee - en vervolgens punten te groeperen op basis van die keuze.

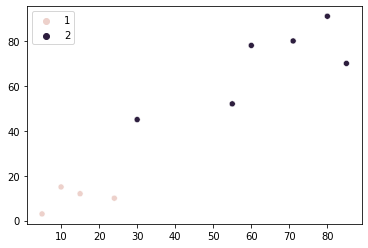
Laten we zeggen dat we hebben besloten dat er zijn twee groepen van onze winkels (punten). Nu moeten we een manier vinden om te begrijpen welke punten bij welke groep horen. Dit kan worden gedaan door één punt te kiezen om te vertegenwoordigen groep 1 en een om te vertegenwoordigen groep 2. Die punten worden gebruikt als referentie bij het meten van de afstand van alle andere punten tot elke groep.

Zeg op die manier punt (5, 3) behoord tot groep 1, en punt (79, 60) naar groep 2. Wanneer u een nieuw punt probeert toe te wijzen (6, 3) voor groepen, moeten we de afstand tot die twee punten meten. In het geval van het punt (6, 3) is dichterbij aan de (5, 3), daarom behoort het tot de groep die door dat punt wordt vertegenwoordigd - groep 1. Op deze manier kunnen we alle punten gemakkelijk in overeenkomstige groepen groeperen.

In dit voorbeeld wordt naast het bepalen van het aantal groepen (clusters) – we kiezen ook een aantal punten als referentie van de afstand voor nieuwe punten van elke groep.

Dat is het algemene idee om overeenkomsten tussen onze winkels te begrijpen. Laten we het in de praktijk brengen - we kunnen eerst de twee referentiepunten kiezen bij willekeurige. Het referentiepunt van groep 1 zal zijn (5, 3) en het referentiepunt van groep 2 zal zijn (10, 15). We kunnen beide punten van onze selecteren numpy array door [0] en [1] indexen en sla ze op in g1 (groep 1) en g2 (groep 2) variabelen:

g1 = points[0]
g2 = points[1]

Nadat we dit hebben gedaan, moeten we de afstand van alle andere punten tot die referentiepunten berekenen. Dit roept een belangrijke vraag op: hoe die afstand te meten. We kunnen in wezen elke afstandsmaat gebruiken, maar laten we voor het doel van deze gids Euclidische afstand_ gebruiken.

Het kan handig zijn om te weten dat de Euclidische afstandsmaat is gebaseerd op de stelling van Pythagoras:

$$
c^2 = a^2 + b^2
$$

Wanneer aangepast aan punten in een vlak - (a1, b1) en (a2, b2), wordt de vorige formule:

$$
c^2 = (a2-a1)^2 + (b2-b1)^2
$$

De afstand is de vierkantswortel van c, dus we kunnen de formule ook schrijven als:

$$
euclidische_{dist} = sqrt[2][(a2 – a1)^2 + (b2 – b1) ^2)]
$$

Tot nu toe hebben we de punten gekozen om groepen weer te geven, en we weten hoe we afstanden moeten berekenen. Laten we nu de afstanden en groepen samenvoegen door elk van onze verzamelde winkelpunten toe te wijzen aan een groep.

Om dat beter te visualiseren zullen we drie lijsten declareren. De eerste die punten van de eerste groep opslaat - points_in_g1. De tweede om punten uit groep 2 op te slaan – points_in_g2, en de laatste - group, te label de punten als ofwel 1 (behoort tot groep 1) of 2 (behoort tot groep 2):

points_in_g1 = []
points_in_g2 = []
group = []

We kunnen nu onze punten doorlopen en de Euclidische afstand tussen hen en elk van onze groepsreferenties berekenen. Elk punt wordt dichterbij aan een van de twee groepen - op basis van welke groep het dichtst bij is, zullen we elk punt toewijzen aan de bijbehorende lijst, terwijl we ook toevoegen 1 or 2 aan de group lijst:

for p in points:
    x1, y1 = p[0], p[1]
    euclidean_distance_g1 = np.sqrt((g1[0] - x1)**2 + (g1[1] - y1)**2)
    euclidean_distance_g2 = np.sqrt((g2[0] - x1)**2 + (g2[1] - y1)**2)
    if euclidean_distance_g1 < euclidean_distance_g2:
        points_in_g1.append(p)
        group.append('1')
    else:
        points_in_g2.append(p)
        group.append('2')

Laten we eens kijken naar de resultaten van deze iteratie om te zien wat er is gebeurd:

print(f'points_in_g1:{points_in_g1}n 
npoints_in_g2:{points_in_g2}n 
ngroup:{group}')

Wat resulteert in:

points_in_g1:[array([5, 3])]
 
points_in_g2:[array([10, 15]), array([15, 12]), 
              array([24, 10]), array([30, 45]), 
              array([85, 70]), array([71, 80]),
              array([60, 78]), array([55, 52]), 
              array([80, 91])]
 
group:[1, 2, 2, 2, 2, 2, 2, 2, 2, 2] 

We kunnen ook het clusterresultaat plotten, met verschillende kleuren op basis van de toegewezen groepen, met behulp van Seaborn's scatterplot() met de group een hue argument:

import seaborn as sns

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

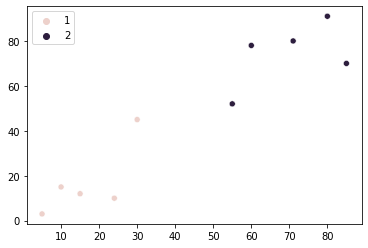
Het is duidelijk te zien dat alleen ons eerste punt is toegewezen aan groep 1, en alle andere punten zijn toegewezen aan groep 2. Dat resultaat wijkt af van wat we in het begin voor ogen hadden. Is er een manier om dat te veranderen, gezien het verschil tussen onze resultaten en onze aanvankelijke verwachtingen? Het lijkt erop dat die er is!

Een benadering is om het proces te herhalen en verschillende punten te kiezen als referenties van de groepen. Dit zal onze resultaten hopelijk meer in lijn brengen met wat we in het begin voor ogen hadden. Deze tweede keer konden we ze niet willekeurig kiezen zoals we eerder deden, maar door een gemiddelde van al onze reeds gegroepeerde punten. Op die manier konden die nieuwe punten in het midden van overeenkomstige groepen worden geplaatst.

Als de tweede groep bijvoorbeeld alleen punten had (10, 15), (30, 45). De nieuwe centraal punt zou zijn (10 + 30)/2 en (15+45)/2 - wat gelijk is aan (20, 30).

Omdat we onze resultaten in lijsten hebben gezet, kunnen we ze eerst converteren naar numpy arrays, selecteer hun xs, ys en verkrijg dan de gemiddelde:

g1_center = [np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()]
g2_center = [np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()]
g1_center, g2_center

Laten we, om het proces met onze nieuwe middelpunten te helpen herhalen, onze vorige code omzetten in een functie, deze uitvoeren en kijken of er wijzigingen zijn in de manier waarop de punten zijn gegroepeerd:

def assigns_points_to_two_groups(g1_center, g2_center):
    points_in_g1 = []
    points_in_g2 = []
    group = []

    for p in points:
        x1, y1 = p[0], p[1]
        euclidean_distance_g1 = np.sqrt((g1_center[0] - x1)**2 + (g1_center[1] - y1)**2)
        euclidean_distance_g2 = np.sqrt((g2_center[0] - x1)**2 + (g2_center[1] - y1)**2)
        if euclidean_distance_g1 < euclidean_distance_g2:
            points_in_g1.append(p)
            group.append(1)
        else:
            points_in_g2.append(p)
            group.append(2)
    return points_in_g1, points_in_g2, group

Laten we de functie aanroepen en de resultaten opslaan in points_in_g1, points_in_g2 en group variabelen:

points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
points_in_g1, points_in_g2, group

En plot ook de scatterplot met de gekleurde punten om de groepsverdeling te visualiseren:

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

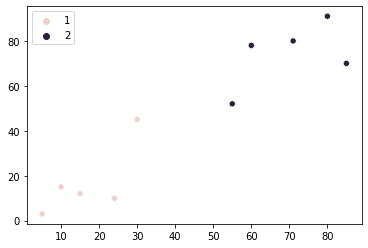
Het lijkt erop dat de clustering van onze punten is beter worden. Maar toch, er zijn twee punten in het midden van de grafiek die aan beide groepen kunnen worden toegewezen, gezien hun nabijheid tot beide groepen. Het algoritme dat we tot nu toe hebben ontwikkeld, wijst beide punten toe aan de tweede groep.

Dit betekent dat we het proces waarschijnlijk nog een keer kunnen herhalen door de middelen van de X'en en Y's te nemen, waardoor er twee nieuwe centrale punten ontstaan (zwaartepunten) aan onze groepen en deze opnieuw toe te wijzen op basis van afstand.

Laten we ook een functie maken om de zwaartepunten bij te werken. Het hele proces kan nu worden teruggebracht tot meerdere aanroepen van die functie:

def updates_centroids(points_in_g1, points_in_g2):
    g1_center = np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()
    g2_center = np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()
    return g1_center, g2_center

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

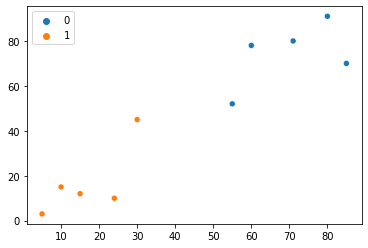
Merk op dat na deze derde iteratie elk van de punten nu tot verschillende clusters behoort. Het lijkt erop dat de resultaten beter worden - laten we het nog een keer doen. Nu naar de vierde iteratie van onze methode:

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

Deze vierde keer hebben we hetzelfde resultaat als de vorige. Dus het lijkt erop dat onze punten niet meer van groep zullen veranderen, ons resultaat heeft een soort van stabiliteit bereikt - het heeft een onveranderlijke staat bereikt, of geconvergeerde. Daarnaast hebben we precies hetzelfde resultaat als we voor ogen hadden voor de 2 groepen. We kunnen ook zien of deze bereikte verdeling zinvol is.

Laten we snel samenvatten wat we tot nu toe hebben gedaan. We hebben onze 10 winkels geografisch verdeeld in twee secties: een in de lagere zuidwestelijke regio's en andere in het noordoosten. Het kan interessant zijn om meer gegevens te verzamelen dan wat we al hebben: omzet, het dagelijkse aantal klanten en nog veel meer. Op die manier kunnen we een rijkere analyse maken en mogelijk interessantere resultaten genereren.

Dergelijke clusterstudies kunnen worden uitgevoerd wanneer een reeds gevestigd merk een gebied wil uitkiezen om een ​​nieuwe winkel te openen. Dan worden er naast de locatie nog veel meer variabelen in aanmerking genomen.

Wat heeft dit allemaal te maken met het K-Means-algoritme?

Tijdens het volgen van deze stappen heb je je misschien afgevraagd wat ze te maken hebben met het K-Means-algoritme. Het proces dat we tot nu toe hebben uitgevoerd is de K-Means algoritme. Kortom, we hebben het aantal groepen/clusters bepaald, willekeurig de beginpunten gekozen en de zwaartepunten in elke iteratie bijgewerkt totdat de clusters samenkwamen. We hebben in feite het hele algoritme met de hand uitgevoerd, waarbij we elke stap zorgvuldig hebben uitgevoerd.

De K in K-Means komt van de aantal clusters die moeten worden ingesteld voordat het iteratieproces wordt gestart. In ons geval K = 2. Deze eigenschap wordt soms gezien als: negatief aangezien er andere clusteringmethoden zijn, zoals hiërarchische clustering, die vooraf geen vast aantal clusters hoeven te hebben.

Door het gebruik van middelen wordt K-means ook gevoelig voor uitbijters en extreme waarden - ze vergroten de variabiliteit en maken het moeilijker voor onze zwaartepunten om hun rol te spelen. Wees je dus bewust van de noodzaak om te presteren extreme waarden en uitbijteranalyse voordat u een clustering uitvoert met behulp van het K-Means-algoritme.

Merk ook op dat onze punten in rechte delen waren gesegmenteerd, er zijn geen bochten bij het maken van de clusters. Dat kan ook een nadeel zijn van het K-Means algoritme.

K-Means heeft ook veel voordelen! Het presteert goed op grote datasets die moeilijk te hanteren kan worden als u bepaalde soorten hiërarchische clusteringalgoritmen gebruikt. Het ook garandeert convergentie, en kan gemakkelijk generaliseren en aanpassen. Daarnaast is het waarschijnlijk het meest gebruikte clusteringalgoritme.

Nu we alle stappen hebben doorgenomen die in het K-Means-algoritme zijn uitgevoerd en alle voor- en nadelen ervan hebben begrepen, kunnen we eindelijk K-Means implementeren met behulp van de Scikit-Learn-bibliotheek.

Hoe K-Means-algoritme te implementeren met behulp van Scikit-Leren

Om ons resultaat dubbel te controleren, laten we dit proces opnieuw doen, maar nu met 3 regels code met sklearn:

from sklearn.cluster import KMeans


kmeans = KMeans(n_clusters=2, random_state=42) 
kmeans.fit(points)
kmeans.labels_

Hier zijn de labels hetzelfde als onze vorige groepen. Laten we snel het resultaat plotten:

sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

De resulterende plot is dezelfde als die uit de vorige sectie.

Met Scikit-Learn kunt u K-Means ook initialiseren voor snellere convergentie door de init='k-means++' argument. In bredere termen, K-middelen++ kiest nog steeds de k aanvankelijke clustercentra willekeurig na een uniforme verdeling. Vervolgens wordt elk volgend clustercentrum gekozen uit de resterende gegevenspunten, niet door alleen een afstandsmaat te berekenen, maar door waarschijnlijkheid te gebruiken. Het gebruik van de waarschijnlijkheid versnelt het algoritme en het is handig bij het omgaan met zeer grote datasets.

De elleboogmethode - Het beste aantal groepen kiezen

Tot nu toe, zo goed! We hebben 10 winkels geclusterd op basis van de Euclidische afstand tussen punten en zwaartepunten. Maar hoe zit het met die twee punten in het midden van de grafiek die iets moeilijker te clusteren zijn? Zouden ze niet ook een aparte groep kunnen vormen? Hebben we echt een fout gemaakt door te kiezen? K = 2 groepen? Misschien hadden we eigenlijk K = 3 groepen? We zouden zelfs meer dan drie groepen kunnen hebben zonder ons daarvan bewust te zijn.

De vraag die hier wordt gesteld is: hoe het aantal groepen (K) in K-Means te bepalen. Om die vraag te beantwoorden, moeten we begrijpen of er een "betere" cluster zou zijn voor een andere waarde van K.

De naïeve manier om daar achter te komen is door punten met verschillende waarden van te clusteren K, dus voor K=2, K=3, K=4, enzovoort:

for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 

Maar, clustering punten voor verschillende Ks alleen zal niet genoeg zijn om te begrijpen of we de ideale waarde hebben gekozen voor K. We hebben een manier nodig om de clusteringkwaliteit voor elk te evalueren K we hebben gekozen.

Handmatig berekenen van de Binnen clustersom van kwadraten (WCSS)

Dit is de ideale plaats om een ​​maatstaf te introduceren van hoeveel onze geclusterde punten dicht bij elkaar liggen. Het beschrijft in wezen hoeveel variantie we hebben binnen een enkele cluster. Deze maatregel heet Binnen clustersom van vierkantenof WCSS in het kort. Hoe kleiner de WCSS, hoe dichter onze punten bij elkaar liggen, daarom hebben we een beter gevormd cluster. De WCSS-formule kan voor een willekeurig aantal clusters worden gebruikt:

$$
WCSS = som(Pi_1 – Centroid_1)^2 + cdots + som(Pi_n – Centroid_n)^2
$$

Nu kunnen we aannemen dat we ervoor hebben gekozen om twee clusters te hebben en proberen de WCSS te implementeren om beter te begrijpen wat de WCSS is en hoe het te gebruiken. Zoals de formule aangeeft, moeten we de kwadratische verschillen tussen alle clusterpunten en zwaartepunten optellen. Dus, als ons eerste punt uit de eerste groep is (5, 3) en ons laatste zwaartepunt (na convergentie) van de eerste groep is (16.8, 17.0), zal de WCSS zijn:

$$
WCSS = som((5,3) – (16.8, 17.0))^2
$$

$$
WCSS = som((5-16.8) + (3-17.0))^2
$$

$$
WCSS = som((-11.8) + (-14.0))^2
$$

$$
WCSS = som((-25.8))^2
$$

$$
WCSS = 335.24
$$

Dit voorbeeld illustreert hoe we de WCSS berekenen voor het ene punt uit het cluster. Maar het cluster bevat meestal meer dan één punt, en we moeten ze allemaal in overweging nemen bij het berekenen van de WCSS. We doen dat door een functie te definiëren die een cluster van punten en zwaartepunten ontvangt en de som van de kwadraten retourneert:

def sum_of_squares(cluster, centroid):
    squares = []
    for p in cluster:
        squares.append((p - centroid)**2)
        ss = np.array(squares).sum()
    return ss

Nu kunnen we de kwadratensom voor elk cluster krijgen:

g1 = sum_of_squares(points_in_g1, g1_center)
g2 = sum_of_squares(points_in_g2, g2_center)

En tel de resultaten op om het totaal te verkrijgen WCSS:

g1 + g2

Dit resulteert in:

2964.3999999999996

Dus, in ons geval, wanneer? K is gelijk aan 2, de totale WCSS is 2964.39. Nu kunnen we Ks omwisselen en de WCSS voor allemaal berekenen. Op die manier kunnen we inzicht krijgen in wat K we moeten ervoor kiezen om onze clustering het beste te laten presteren.

Berekenen WCSS gebruik Scikit-Leren

Gelukkig hoeven we de WCSS niet voor elk handmatig te berekenen K. Na het uitvoeren van de K-Means-clustering voor het gegeven aantal clusters, kunnen we de WCSS ervan verkrijgen met behulp van de inertia_ attribuut. Nu kunnen we terug naar onze K-Means for loop, gebruik het om het aantal clusters te wijzigen en de bijbehorende WCSS-waarden op te sommen:

wcss = [] 
for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 
    wcss.append(kmeans.inertia_)
wcss

Merk op dat de tweede waarde in de lijst precies dezelfde is die we eerder hebben berekend voor K = 2:

[18272.9, # For k=1 
 2964.3999999999996, # For k=2
 1198.75, # For k=3
 861.75,
 570.5,
 337.5,
 175.83333333333334,
 79.5,
 17.0,
 0.0]

Laten we, om die resultaten te visualiseren, onze Ks samen met de WCSS-waarden:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
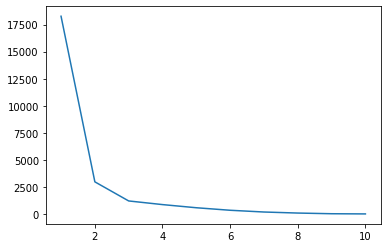
plt.plot(ks, wcss)

Er is een onderbreking op een perceel wanneer: x = 2, een dieptepunt in de lijn, en een nog lagere wanneer x = 3. Merk op dat het ons herinnert aan de vorm van een elleboog. Door de Ks samen met de WCSS te plotten, gebruiken we de Elleboog Methode: om het aantal Ks te kiezen. En de gekozen K is precies het laagste elleboogpunt, dus het zou zijn 3 in plaats van 2, in ons geval:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
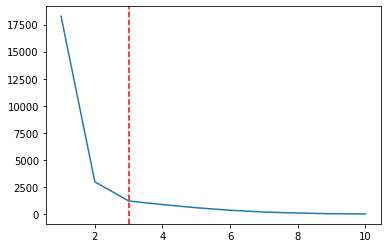
plt.plot(ks, wcss);
plt.axvline(3, linestyle='--', color='r')

We kunnen het K-Means-clusteralgoritme opnieuw uitvoeren om te zien hoe onze gegevens eruit zouden zien met drie clusters:

kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(points)
sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

We waren al blij met twee clusters, maar volgens de elleboogmethode zouden drie clusters beter passen bij onze data. In dit geval zouden we drie soorten winkels hebben in plaats van twee. Voordat we de elleboogmethode gebruikten, dachten we aan winkelclusters in het zuidwesten en noordoosten, nu hebben we ook winkels in het centrum. Misschien is dat een goede locatie om een ​​andere winkel te openen, omdat er dan minder concurrentie in de buurt is.

Alternatieve maatregelen voor clusterkwaliteit

Er zijn ook andere maatregelen die kunnen worden gebruikt bij het evalueren van clusterkwaliteit:

• Silhouetscore – analyseert niet alleen de afstand tussen intra-clusterpunten, maar ook tussen clusters onderling
• Tussen clusters Som van vierkanten (BCSS) – metriek complementair aan de WCSS
• Som van kwadratenfout (ZZO)
• Maximale straal – meet de grootste afstand van een punt tot zijn zwaartepunt
• Gemiddelde straal – de som van de grootste afstand van een punt tot zijn zwaartepunt gedeeld door het aantal clusters.

Het wordt aanbevolen om te experimenteren en elk van hen te leren kennen, aangezien, afhankelijk van het probleem, sommige van de alternatieven meer toepasbaar kunnen zijn dan de meest gebruikte statistieken (WCSS en Silhouette-score).

Uiteindelijk willen we, zoals bij veel datawetenschapsalgoritmen, de variantie binnen elk cluster verminderen en de variantie tussen verschillende clusters maximaliseren. We hebben dus meer gedefinieerde en scheidbare clusters.

K-Means toepassen op een andere dataset

Laten we gebruiken wat we hebben geleerd op een andere dataset. Deze keer zullen we proberen groepen van vergelijkbare wijnen te vinden.

We beginnen met importeren pandas om de te lezen wine-clustering CSV (Door komma's gescheiden waarden) bestand in a Dataframe structuur:

import pandas as pd

df = pd.read_csv('wine-clustering.csv')

Laten we na het laden een kijkje nemen in de eerste vijf gegevensrecords met de head() methode:

df.head()

Dit resulteert in:

	Alcohol 	Malic_Acid 	Ash 	Ash_Alcanity 	Magnesium 	Total_Phenols 	Flavanoids 	Nonflavanoid_Phenols 	Proanthocyanins 	Color_Intensity 	Hue 	OD280 	Proline
0 	14.23 		1.71 		2.43 	15.6 			127 		2.80 			3.06 		0.28 					2.29 				5.64 				1.04 	3.92 	1065
1 	13.20 		1.78 		2.14 	11.2 			100 		2.65 			2.76 		0.26 					1.28 				4.38 				1.05 	3.40 	1050
2 	13.16 		2.36 		2.67 	18.6 			101 		2.80 			3.24 		0.30 					2.81 				5.68 				1.03 	3.17 	1185
3 	14.37 		1.95 		2.50 	16.8 			113 		3.85 			3.49 		0.24 					2.18 				7.80 				0.86 	3.45 	1480
4 	13.24 		2.59 		2.87 	21.0 			118 		2.80 			2.69 		0.39 					1.82 				4.32 				1.04 	2.93 	735

We hebben veel metingen van stoffen die aanwezig zijn in wijnen. Hier hoeven we categorische kolommen ook niet te transformeren omdat ze allemaal numeriek zijn. Laten we nu eens kijken naar de beschrijvende statistieken met de describe() methode:

df.describe().T 

De beschrijven tafel:

 						count 	mean 		std 		min 	25% 	50% 	75% 		max
Alcohol 				178.0 	13.000618 	0.811827 	11.03 	12.3625 13.050 	13.6775 	14.83
Malic_Acid 				178.0 	2.336348 	1.117146 	0.74 	1.6025 	1.865 	3.0825 		5.80
Ash 					178.0 	2.366517 	0.274344 	1.36 	2.2100 	2.360 	2.5575 		3.23
Ash_Alcanity 			178.0 	19.494944 	3.339564 	10.60 	17.2000 19.500 	21.5000 	30.00
Magnesium 				178.0 	99.741573 	14.282484 	70.00 	88.0000 98.000 	107.0000 	162.00
Total_Phenols 			178.0 	2.295112 	0.625851 	0.98 	1.7425 	2.355 	2.8000 		3.88
Flavanoids 				178.0 	2.029270 	0.998859 	0.34 	1.2050 	2.135 	2.8750 		5.08
Nonflavanoid_Phenols 	178.0 	0.361854 	0.124453 	0.13 	0.2700 	0.340 	0.4375 		0.66
Proanthocyanins 		178.0 	1.590899 	0.572359 	0.41 	1.2500 	1.555 	1.9500 		3.58
Color_Intensity 		178.0 	5.058090 	2.318286 	1.28 	3.2200 	4.690 	6.2000 		13.00
Hue 					178.0 	0.957449 	0.228572 	0.48 	0.7825 	0.965 	1.1200 		1.71
OD280 					178.0 	2.611685 	0.709990 	1.27 	1.9375 	2.780 	3.1700 		4.00
Proline 				178.0 	746.893258 	314.907474 	278.00 	500.500 673.500 985.0000 	1680.00

Door naar de tafel te kijken, is het duidelijk dat er wat is variabiliteit in de gegevens – voor sommige kolommen zoals Alchool er is meer, en voor anderen, zoals: Malic_Acid, minder. Nu kunnen we controleren of die er zijn nullof NaN waarden in onze dataset:

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 13 columns):
 #   Column                Non-Null Count  Dtype  
---  ------                --------------  -----  
 0   Alcohol               178 non-null    float64
 1   Malic_Acid            178 non-null    float64
 2   Ash                   178 non-null    float64
 3   Ash_Alcanity          178 non-null    float64
 4   Magnesium             178 non-null    int64  
 5   Total_Phenols         178 non-null    float64
 6   Flavanoids            178 non-null    float64
 7   Nonflavanoid_Phenols  178 non-null    float64
 8   Proanthocyanins       178 non-null    float64
 9   Color_Intensity       178 non-null    float64
 10  Hue                   178 non-null    float64
 11  OD280                 178 non-null    float64
 12  Proline               178 non-null    int64  
dtypes: float64(11), int64(2)
memory usage: 18.2 KB

Het is niet nodig om gegevens te verwijderen of in te voeren, aangezien er geen lege waarden in de gegevensset zijn. We kunnen een Seaborn gebruiken pairplot() om de datadistributie te zien en om te controleren of de dataset kolommenparen vormt die interessant kunnen zijn voor clustering:

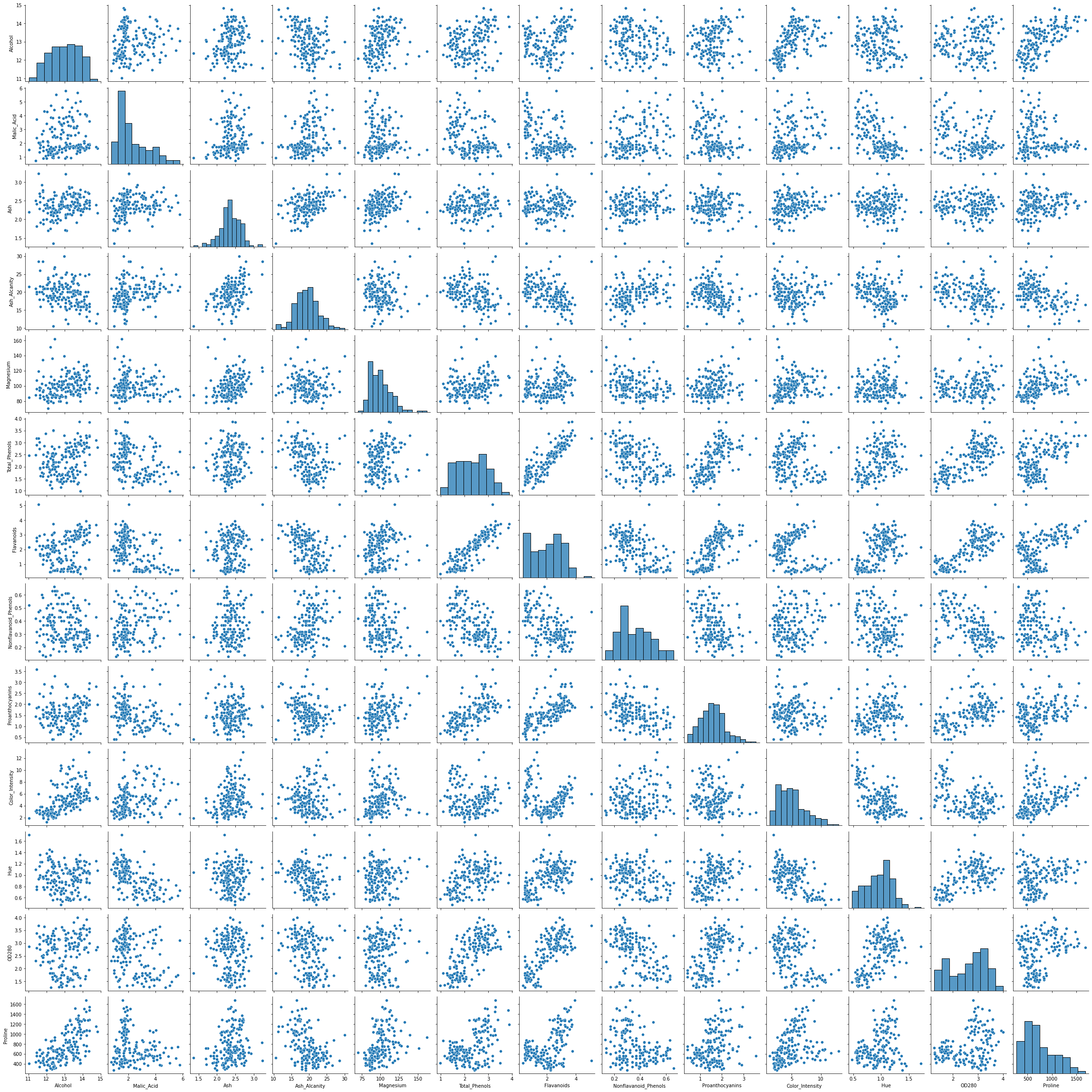
sns.pairplot(df)

Door naar de pairplot te kijken, lijken twee kolommen veelbelovend voor clusteringdoeleinden - Alcohol en OD280 (wat een methode is om de eiwitconcentratie in wijnen te bepalen). Het lijkt erop dat er 3 verschillende clusters zijn op percelen die er twee combineren.

Er zijn ook andere kolommen die met elkaar in verband lijken te staan. vooral: Alcohol en Total_Phenols en Alcohol en Flavanoids. Ze hebben geweldige lineaire relaties die kunnen worden waargenomen in de pairplot.

Aangezien onze focus ligt op clustering met K-Means, laten we één paar kolommen kiezen, zeg Alcohol en OD280en test de elleboogmethode voor deze dataset.

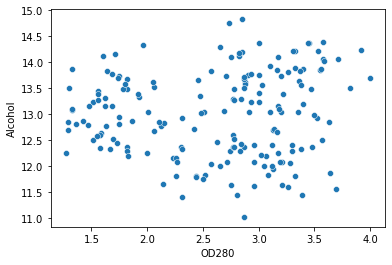
Laten we de scatterplot plotten met die twee kolommen als de as om de punten die we in groepen willen verdelen nader te bekijken:

sns.scatterplot(data=df, x='OD280', y='Alcohol')

Nu kunnen we onze kolommen definiëren en de elleboogmethode gebruiken om het aantal clusters te bepalen. We zullen het algoritme ook starten met kmeans++ gewoon om ervoor te zorgen dat het sneller convergeert:

values = df[['OD280', 'Alcohol']]

wcss_wine = [] 
for i in range(1, 11): 
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(values) 
    wcss_wine.append(kmeans.inertia_)

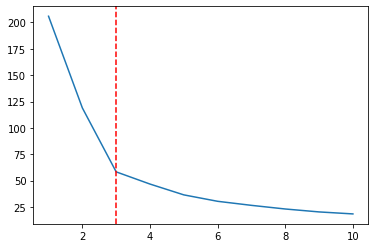
We hebben de WCSS berekend, zodat we de resultaten kunnen plotten:

clusters_wine = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
plt.plot(clusters_wine, wcss_wine)
plt.axvline(3, linestyle='--', color='r')

Volgens de elleboogmethode zouden we hier 3 clusters moeten hebben. Laten we voor de laatste stap onze punten clusteren in 3 clusters en de clusters uitzetten die worden geïdentificeerd door kleuren:

kmeans_wine = KMeans(n_clusters=3, random_state=42)
kmeans_wine.fit(values)
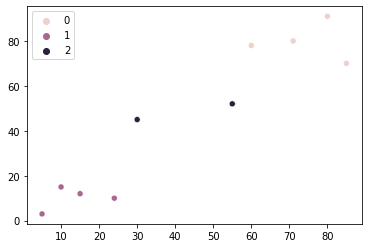
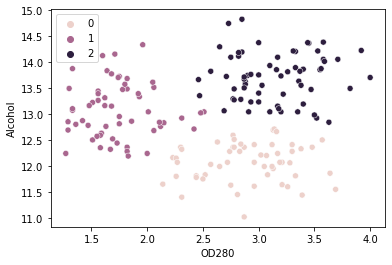
sns.scatterplot(x = values['OD280'], y = values['Alcohol'], hue=kmeans_wine.labels_)

We kunnen clusters zien 0, 1 en 2 in de grafiek. Op basis van onze analyse, groep 0 heeft wijnen met een hoger eiwitgehalte en een lager alcoholgehalte, groep 1 heeft wijnen met een hoger alcoholgehalte en een laag eiwitgehalte, en groep 2 heeft zowel een hoog eiwitgehalte als een hoog alcoholgehalte in zijn wijnen.

Dit is een zeer interessante dataset en ik moedig je aan om verder in de analyse te gaan door de data na normalisatie en PCA te clusteren – ook door de resultaten te interpreteren en nieuwe verbanden te vinden.

Conclusie

K-middelen clustering is een eenvoudig maar zeer effectief algoritme voor machine learning zonder toezicht voor gegevensclustering. Het clustert gegevens op basis van de Euclidische afstand tussen gegevenspunten. K-Means clustering-algoritme heeft veel toepassingen voor het groeperen van tekstdocumenten, afbeeldingen, video's en nog veel meer.