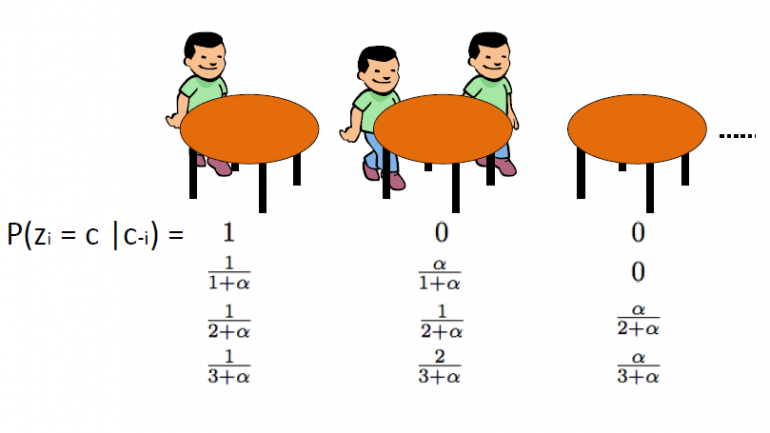Het Dirichlet-proces het Chinese restaurantproces en andere representaties

• 20 mei 2014
• Vasilis Vryniotis
• . Geen commentaar

Dit artikel is het derde deel van de serie over clustering met Dirichlet Process Mixture Models. De vorige keer dat we het Eindige Mengsel Model definieerden op basis van Dirichlet Verdeling en we stelden vragen hoe we dit specifieke model oneindig kunnen maken. We bespraken kort het idee om de limiet van het model te nemen wanneer het k-aantal clusters oneindig is, maar omdat we benadrukten dat het bestaan ​​van een dergelijk object niet triviaal is (met andere woorden, hoe nemen we eigenlijk de limiet van een model? "?). Ter herinnering, de reden waarom we k oneindig willen nemen, is omdat we op deze manier een niet-parametrisch model hebben dat ons niet verplicht om het totale aantal clusters binnen de gegevens vooraf te definiëren.

Update: het Datumbox Machine Learning Framework is nu open-source en gratis voor Download. Bekijk het pakket com.datumbox.framework.machinelearning.clustering om de implementatie van Dirichlet Process Mixture Models in Java te zien.

Hoewel het ons doel is om een ​​model te bouwen dat clustering op datasets kan uitvoeren, moeten we eerst discussiëren over Dirichlet-processen. We zullen zowel de strikte wiskundige definities als de meer intuïtieve uitleg van DP geven en we zullen manieren bespreken om het proces te construeren. Die constructies / representaties kunnen worden gezien als een manier om gebeurtenissen van het Dirichlet-proces in het 'echte leven' te vinden.

Ondanks dat ik heb geprobeerd mijn onderzoeksrapport zo aan te passen dat deze blogposts gemakkelijker te volgen zijn, is het nog steeds belangrijk om de nodige wiskundige tools en distributies te definiëren voordat we de modellen gaan gebruiken. Dirichlet-procesmodellen zijn een onderwerp van actief onderzoek, maar ze vereisen wel een goed begrip van statistiek en stochastische processen voordat ze kunnen worden gebruikt. Een ander probleem is dat, zoals we in dit artikel zullen zien, Dirichlet-processen op verschillende manieren kunnen worden weergegeven / geconstrueerd. Als gevolg hiervan gebruiken verschillende academische papers volledig verschillende notatie / conventies en onderzoeken ze het probleem vanuit verschillende gezichtspunten. In deze post probeer ik ze zo eenvoudig mogelijk uit te leggen en gebruik ik dezelfde notatie. Hopelijk wordt het duidelijker met de twee aankomende artikelen die zich richten op de definitie van Dirichlet-procesmengselmodellen en op hoe ze daadwerkelijk kunnen worden gebruikt om clusteranalyse uit te voeren.

1. Definitie van het Dirichlet-proces

Een Dirichlet-proces over een Θ-ruimte is een stochastisch proces. Het is een kansverdeling over "kansverdelingen over Θ ruimte" en een daaruit putten is een discrete verdeling. Formeler is een Dirichlet-verdeling een verdeling over waarschijnlijkheidsmetingen. EEN kansmaat is een functie van deelverzamelingen van ruimte Θ tot [0,1]. G is een DP gedistribueerde willekeurige kansmaat, aangeduid als , als voor een partitie (A₁,…EEN_n) van ruimte Θ dat hebben we .

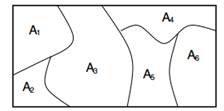
Figuur 1: Marges op eindige partities zijn Dirichlet gedistribueerd.

De DP heeft twee parameters: De eerste is de basisverdeling G₀ wat als een middel dient . De tweede is de sterkteparameter α die strikt positief is en dient als inverse variantie . Het bepaalt de omvang van de herhaling van de waarden van de outputverdeling. Hoe hoger de waarde van a, hoe kleiner de herhaling; hoe kleiner de waarde, hoe hoger de herhaling van de waarden van de outputverdeling. Ten slotte is de Θ-ruimte de parameterruimte waarop we de DP definiëren. Bovendien is de ruimte Θ ook de definitieruimte van G₀ wat hetzelfde is als die van G.

Een eenvoudiger en meer intuïtieve manier om een ​​Dirichlet-proces uit te leggen is het volgende. Stel dat we een ruimte Θ hebben die op elke eindige manier kan worden verdeeld (A₁,…,EEN_n) en een kansverdeling G die kansen aan hen toewijst. De G is een specifieke kansverdeling over Θ maar er zijn nog veel meer. Het Dirichlet-proces op Θ modelleert precies dit; het is een verdeling over alle mogelijke kansverdelingen op ruimte Θ. Het Dirichlet-proces is geparametriseerd met de G₀ basisfunctie en de α-concentratieparameter. We kunnen zeggen dat G wordt verdeeld volgens DP met parameters α en G₀ als de gezamenlijke verdeling van de kansen die G toekent aan de partities van Θ de Dirichlet-verdeling volgt. Als alternatief kunnen we zeggen dat de kansen die G toewijst aan een eindige partitie van Θ Dirichlet Distribution volgt.

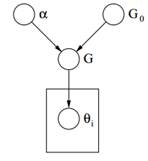
Figuur 2: grafisch model van Dirichlet-proces

Eindelijk hierboven zien we de grafisch model van een DP. We moeten opmerken dat α een scalaire hyperparameter is, G₀ is de basisverdeling van DP, G een willekeurige verdeling over Θ parameterruimte bemonsterd uit de DP die kansen toewijst aan de parameters en θ_i is een parametervector die wordt getrokken uit de G-verdeling en het is een element van Θ ruimte.

2. Posterior Dirichlet-processen

De posterieure Dirichlet-processen werden besproken door Ferguson. We beginnen met het trekken van een willekeurige kansmaat G uit een Dirichlet-proces, . Aangezien G een kansverdeling is over Θ kunnen we ook uit deze verdeling bemonsteren en onafhankelijke identiek verdeelde monsters trekken θ₁,…, Θ_n ~ G. Aangezien putten uit een Dirichlet-proces discrete distributies zijn, kunnen we representeren WAAR is een korte notatie voor wat een deltafunctie is die 1 als nodig heeft en 0 elders. Een interessant effect hiervan is dat aangezien G op deze manier is gedefinieerd, er een positieve kans is dat verschillende monsters dezelfde waarde hebben . Zoals we later zullen zien, creëert dit een clusteringseffect dat kan worden gebruikt om clusteranalyse uit te voeren op datasets.

Met behulp van de bovenstaande definities en observaties willen we de posterior van het Dirichlet-proces schatten, gegeven de monsters θ. Toch weten we dat en door gebruik te maken van de Bayes Rules en de Conjugacy tussen Dirichlet en Multinomial hebben we dat en .

Vergelijking 1: posterieur dirichlet-proces

Deze eigenschap is erg belangrijk en wordt gebruikt door de verschillende DP-representaties.

3. Dirichlet-procesrepresentaties

In de vorige segmenten hebben we het Dirichlet-proces gedefinieerd en het theoretische model gepresenteerd. Een belangrijke vraag die we moeten beantwoorden, is hoe weten we dat zo'n object bestaat en hoe we dat kunnen construeren en vertegenwoordigen een Dirichlet-proces.

De eerste aanwijzingen voor het bestaan ​​waren afkomstig van Ferguson die de Kolmogorov Consistentie Stelling gebruikte, gaf de definitie van een Dirichlet-proces en beschreef het Posterior Dirichlet-proces. Voortzetting van zijn onderzoek, Blackwell en MacQueen gebruikte de stelling van de Finetti om het bestaan ​​van zo'n willekeurige waarschijnlijkheidsmeting te bewijzen en introduceerde het Blackwell-MacQueen urnschema dat voldoet aan de eigenschappen van Dirichlet Process. In 1994 sethuraman zorgde voor een extra eenvoudige en directe manier om een ​​DP te bouwen door de Stick-breaking constructie te introduceren. Tenslotte werd er nog een vertegenwoordiging verzorgd door Aldous die het Chinese restaurantproces introduceerde als een effectieve manier om een ​​Dirichlet-proces te construeren.

De verschillende representaties van het Dirichlet-proces zijn wiskundig equivalent, maar hun formulering verschilt omdat ze het probleem vanuit verschillende gezichtspunten onderzoeken. Hieronder presenteren we de meest voorkomende representaties in de literatuur en richten we ons op het Chinese restaurantproces, dat een eenvoudige en computationeel efficiënte manier biedt om inferentiealgoritmen voor het Dirichlet-proces te construeren.

3.1 Het urnschema van Blackwell-MacQueen

Het urnschema van Blackwell-MacQueen kan worden gebruikt om een ​​Dirichlet-proces weer te geven en werd geïntroduceerd door Blackwell en MacQueen. Het is gebaseerd op het Pólya urnschema dat kan worden gezien als het tegenovergestelde model van bemonstering zonder vervanging. Bij het Pólya urnschema gaan we ervan uit dat we een niet-transparante urn hebben met gekleurde ballen en trekken we ballen willekeurig. Wanneer we een bal tekenen, observeren we de kleur, plaatsen we hem terug in de urn en voegen we een extra bal van dezelfde kleur toe. Blackwell en MacQueen gebruiken een soortgelijk schema om een ​​Dirichlet-proces te construeren.

Dit schema levert een reeks van θ op₁, θ₂, ... met voorwaardelijke kansen . In dit schema gaan we ervan uit dat G₀ is een verdeling over kleuren en elk θ_n vertegenwoordigt de kleur van de bal die in de urn is geplaatst. De algoritme is als volgt:

· We beginnen met een lege urn.

· Waarschijnlijk evenredig met α wij tekenen en we voegen een bal van deze kleur toe aan de urn.

· Met kans evenredig aan n-1 trekken we een willekeurige bal uit de urn, observeren we de kleur, plaatsen we hem terug in de urn en voegen we een extra bal van dezelfde kleur toe aan de urn.

Eerder begonnen we met een Dirichlet-proces en hebben we het Blackwell-MacQueen-schema afgeleid. Laten we nu omgekeerd beginnen met het Blackwell-MacQueen-schema en de DP afleiden. Sinds θ_i werden op een iid manier uit G getrokken, hun gezamenlijke distributie zal onveranderlijk zijn voor alle eindige permutaties en dus zijn ze uitwisselbaar. Door de stelling van de Finetti te gebruiken, hebben we dus dat er een verdeling moet zijn over maatregelen om ze te maken en deze verdeling is het Dirichlet-proces. Als resultaat bewijzen we dat het Blackwell-MacQueen urnschema een representatie is van DP en het geeft ons een concrete manier om het te construeren. Zoals we later zullen zien, is dit schema wiskundig equivalent aan het Chinese restaurantproces.

3.2 De stokbrekende constructie

De Stick-breaking constructie is een alternatieve manier om een ​​Dirichlet-proces te vertegenwoordigen dat werd geïntroduceerd door sethuraman. Het is een constructieve manier om de distributie en gebruikt de naar analogie: We nemen aan dat we een stok van lengte 1 hebben, die breken we op positie β₁ en we kennen π toe₁ gelijk aan de lengte van het deel van de stok dat we hebben gebroken. We herhalen hetzelfde proces om π te verkrijgen₂, Pi₃,… enzovoort; door de manier waarop dit schema is gedefinieerd kunnen we het oneindig blijven doen.

Op basis van het bovenstaande is de π_k kan worden gemodelleerd als Wanneer de terwijl zoals in de vorige schema's de θ rechtstreeks bemonsterd worden door de basisverdeling . Bijgevolg kan de G-verdeling worden geschreven als een som van deltafuncties gewogen met π_k kansen die gelijk is aan . Zo biedt de Stick-brekende constructie ons een eenvoudige en intuïtieve manier om een ​​Dirichlet-proces te construeren.

3.3 Het Chinese restaurantproces

The Chinese Restaurant Process, dat werd geïntroduceerd door Aldous, is een andere effectieve manier om een ​​Dirichlet-proces weer te geven en het kan rechtstreeks worden gekoppeld aan het urnschema van Blackwell-MacQueen. Deze regeling maakt gebruik van de naar analogie: We gaan ervan uit dat er een Chinees restaurant is met oneindig veel tafels. Als de klanten het restaurant binnenkomen, zitten ze willekeurig aan een van de bezette tafels of kiezen ze ervoor om aan de eerst beschikbare lege tafel te zitten.

De CRP definieert een verdeling over de ruimte van partities van de positieve gehele getallen. We beginnen met tekenen θ₁, ... θ_n van Blackwell-MacQueen urnschema. Zoals we in de vorige segmenten hebben besproken, verwachten we een clusteringseffect te zien en dus zal het totale aantal unieke θ waarden k aanzienlijk kleiner zijn dan n. Dit definieert dus een partitie van de set {1,2,…, n} in k-clusters. Bijgevolg leidt het tekenen van het urnschema van Blackwell-MacQueen tot een willekeurige partitie van de {1,2,…, n} set. Het Chinese restaurantproces is dit veroorzaakt verdeling over partities. Het algoritme is als volgt:

· We beginnen met een leeg restaurant.

· De 1^st klant zit altijd op 1^st tafel

· De n + 1^th klant heeft 2 opties:

o Ga waarschijnlijk op de 1e onbezette tafel zitten

o Ga waarschijnlijk op een van de kt bezette tafels zitten
WAAR is het aantal mensen dat op die tafel zit

Waar α de verspreidingswaarde van DP is en n het totale aantal klanten in het restaurant op een bepaald moment. De latente variabele z_i slaat het tafelnummer van de i op^th klant en neemt waarden van 1 tot k_n waar k_n is het totaal aantal bezette tafels wanneer n klanten in het restaurant zijn. We moeten opmerken dat de k_n zal altijd kleiner of gelijk zijn aan n en gemiddeld gaat het om . Ten slotte moeten we opmerken dat de kans op tafelindeling is onveranderlijk voor permutaties. Dus de z_i is uitwisselbaar, wat inhoudt dat tafels met dezelfde grootte van klanten dezelfde kans hebben.

Het Chinese restaurantproces is sterk verbonden met het Pólya urnschema en het Dirichlet-proces. De CRP is een manier om een verdeling over partities (tabeltoewijzingen) van n punten en kan worden gebruikt als een prior op de ruimte van latente variabele z_i welke bepaalt de clustertoewijzingen. De CRP is gelijk aan het urnschema van Pólya, met het enige verschil dat het geen parameters toewijst aan elke tabel / cluster. Gaan van CRP tot Pólya's urnschema wij tekenen voor alle tabellen k = 1,2 ... en dan voor elke x_i die is gegroepeerd in tabel z_i wijs een toe . Met andere woorden toewijzen aan de nieuwe x_i de parameter θ van de tabel. Eindelijk sinds we kunnen niet toewijzen Van de θ tot oneindige tafels vanaf het begin, kunnen we gewoon een nieuwe θ toewijzen telkens wanneer iemand aan een nieuwe tafel zit. Vanwege al het bovenstaande kan de CRP ons helpen rekenkundig efficiënte algoritmen te bouwen om clusteranalyse uit te voeren op datasets.

In deze post bespraken we het Dirichlet-proces en verschillende manieren om het te construeren. We zullen de bovenstaande ideeën gebruiken in het volgende artikel. We zullen het Dirichlet Process Mixture Model introduceren en we zullen de Chinese Restaurant Representation gebruiken om het Dirichlet Process en de preform Cluster Analysis te construeren. Maak je geen zorgen als je een paar punten hebt gemist, want de zaken zullen duidelijker worden met de volgende twee artikelen.

Ik hoop dat je dit bericht interessant vond. Als dat zo is, neem dan even de tijd om het op Facebook en Twitter te delen. 🙂