Big O-notasjon og algoritmeanalyse med Python-eksempler

Introduksjon

Det er vanligvis flere måter å løse problemet på ved hjelp av et dataprogram. For eksempel er det flere måter å sortere elementer i en matrise – du kan bruke slå sammen, boble sortering, innsettings sortering, og så videre. Alle disse algoritmene har sine egne fordeler og ulemper, og utviklerens jobb er å veie dem for å kunne velge den beste algoritmen som skal brukes uansett bruk. Med andre ord er hovedspørsmålet hvilken algoritme du skal bruke for å løse et spesifikt problem når det finnes flere løsninger på problemet.

Algoritmeanalyse refererer til analysen av kompleksiteten til forskjellige algoritmer og finne den mest effektive algoritmen for å løse problemet. Big-O-notasjon er et statistisk mål som brukes for å beskrive kompleksiteten til algoritmen.

I denne veiledningen vil vi først ta en kort gjennomgang av algoritmeanalyse og deretter ta en dypere titt på Big-O-notasjonen. Vi skal se hvordan Big-O-notasjon kan brukes til å finne algoritmekompleksitet ved hjelp av forskjellige Python-funksjoner.

Hvorfor er algoritmeanalyse viktig?

For å forstå hvorfor algoritmeanalyse er viktig, vil vi ta hjelp av et enkelt eksempel. Anta at en leder gir en oppgave til to av sine ansatte om å designe en algoritme i Python som beregner faktoren til et tall som er lagt inn av brukeren. Algoritmen utviklet av den første ansatte ser slik ut:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Legg merke til at algoritmen ganske enkelt tar et heltall som et argument. Inne i fact() funksjon en variabel kalt product er initialisert til 1. En loop kjøres fra 1 til n og under hver iterasjon, verdien i product multipliseres med tallet som itereres av løkken og resultatet lagres i product variabel igjen. Etter at loopen er utført, vil product variabelen vil inneholde faktoren.

På samme måte utviklet den andre ansatte også en algoritme som beregner faktoren til et tall. Den andre ansatte brukte en rekursiv funksjon for å beregne faktoren til tallet n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Lederen må bestemme hvilken algoritme som skal brukes. For å gjøre det har de bestemt seg for å velge hvilken algoritme som kjører raskere. En måte å gjøre det på er å finne tiden det tar å kjøre koden på samme inngang.

I Jupyter-notisboken kan du bruke %timeit bokstavelig etterfulgt av funksjonskallet for å finne tiden det tar for funksjonen å utføre:

%timeit fact(50)

Dette vil gi oss:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Utgangen sier at algoritmen tar 9 mikrosekunder (pluss/minus 45 nanosekunder) per sløyfe.

På samme måte kan vi beregne hvor lang tid den andre tilnærmingen tar å utføre:

%timeit fact2(50)

Dette vil resultere i:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Den andre algoritmen som involverer rekursjon tar 15 mikrosekunder (pluss/minus 427 nanosekunder).

Utførelsestiden viser at den første algoritmen er raskere sammenlignet med den andre algoritmen som involverer rekursjon. Når du arbeider med store innganger, kan ytelsesforskjellen bli mer betydelig.

Imidlertid er utførelsestid ikke en god beregning for å måle kompleksiteten til en algoritme siden den avhenger av maskinvaren. En mer objektiv kompleksitetsanalyseverdi for en algoritme er nødvendig. Det er her Stor O-notasjon kommer til å spille.

Algoritmeanalyse med Big-O-notasjon

Big-O-notasjon angir forholdet mellom input til algoritmen og trinnene som kreves for å utføre algoritmen. Det er merket med en stor "O" etterfulgt av en åpnings- og lukkeparentes. Inne i parentesen presenteres forholdet mellom input og trinnene tatt av algoritmen ved å bruke "n".

Nøkkelen er – Big-O er ikke interessert i en Spesielt forekomst der du kjører en algoritme, for eksempel fact(50), men heller, hvor godt gjør det skala gitt økende innspill. Dette er en mye bedre beregning for å evaluere enn konkret tid for en konkret instans!

For eksempel, hvis det er en lineært forhold mellom inngangen og trinnet som tas av algoritmen for å fullføre dens utførelse, vil Big-O-notasjonen som brukes være O (n). Tilsvarende er Big-O-notasjonen for kvadratiske funksjoner is O(n²).

For å bygge intuisjon:

• O (n): kl n=1, 1 steg er tatt. På n=10, 10 steg er tatt.
• O(n²): kl n=1, 1 steg er tatt. På n=10, 100 steg er tatt.

At n=1, disse to ville prestere det samme! Dette er en annen grunn til at det er bedre å observere forholdet mellom input og antall trinn for å behandle innspillet enn bare å evaluere funksjoner med noen konkrete input.

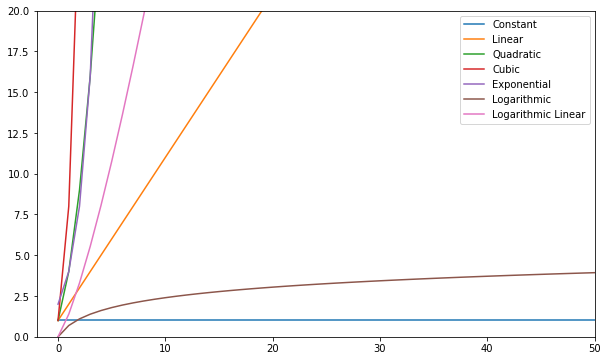
Følgende er noen av de vanligste Big-O-funksjonene:

Navn	Stor O
Konstant	O (c)
Linear	O (n)
kvadratisk	O(n²)
Cubic	O(n³)
Eksponentiell	O(2ⁿ)
Logaritmisk	O (logg (n))
Logg lineær	O(nlog(n))

Du kan visualisere disse funksjonene og sammenligne dem:

Generelt sett – alt verre enn lineært anses som en dårlig kompleksitet (dvs. ineffektiv) og bør unngås hvis mulig. Lineær kompleksitet er greit og vanligvis et nødvendig onde. Logaritmikk er bra. Constant er fantastisk!

For å få en ide om hvordan en Big-O beregnes, la oss ta en titt på noen eksempler på konstant, lineær og kvadratisk kompleksitet.

Konstant kompleksitet – O(C)

Kompleksiteten til en algoritme sies å være konstant hvis trinnene som kreves for å fullføre utførelsen av en algoritme forblir konstante, uavhengig av antall innganger. Den konstante kompleksiteten er betegnet med O (c) hvor c kan være et hvilket som helst konstant tall.

La oss skrive en enkel algoritme i Python som finner kvadratet til det første elementet i listen og deretter skriver det ut på skjermen:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

I manuset ovenfor, uavhengig av inngangsstørrelsen, eller antall elementer i inndatalisten items, utfører algoritmen kun 2 trinn:

1. Finne kvadratet til det første elementet
2. Skriver ut resultatet på skjermen.

Derfor forblir kompleksiteten konstant.

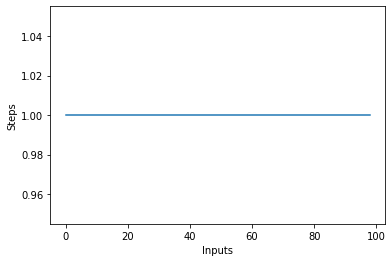
Hvis du tegner et linjeplott med varierende størrelse på items input på X-aksen og antall trinn på Y-aksen, vil du få en rett linje. La oss lage et kort skript for å hjelpe oss med å visualisere dette. Uansett antall innganger, forblir antall utførte trinn det samme:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Lineær kompleksitet – O (n)

Kompleksiteten til en algoritme sies å være lineær hvis trinnene som kreves for å fullføre utførelsen av en algoritme øker eller reduseres lineært med antall innganger. Lineær kompleksitet er betegnet med O (n).

I dette eksemplet, la oss skrive et enkelt program som viser alle elementene i listen til konsollen:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Kompleksiteten til linear_algo() funksjonen er lineær i eksemplet ovenfor siden antall iterasjoner av for-løkken vil være lik størrelsen på inngangen items matrise. For eksempel, hvis det er 4 elementer i items listen, vil for-løkken bli utført 4 ganger.

La oss raskt lage et plott for den lineære kompleksitetsalgoritmen med antall innganger på x-aksen og antall trinn på y-aksen:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Dette vil resultere i:

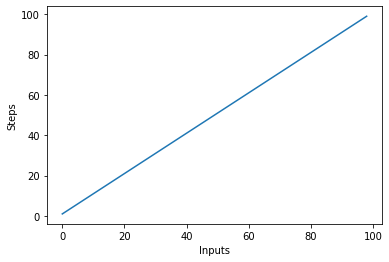
En viktig ting å merke seg er at med store innganger har konstanter en tendens til å miste verdi. Dette er grunnen til at vi vanligvis fjerner konstanter fra Big-O-notasjonen, og et uttrykk som O(2n) er vanligvis forkortet til O(n). Både O(2n) og O(n) er lineære – det lineære forholdet er det som betyr noe, ikke den konkrete verdien. La oss for eksempel endre linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Det er to for-løkker som itererer over inngangen items liste. Derfor blir kompleksiteten til algoritmen O (2n), men i tilfelle av uendelige elementer i inndatalisten, er to ganger av uendelig fortsatt lik uendelig. Vi kan ignorere konstanten 2 (siden den til syvende og sist er ubetydelig) og kompleksiteten til algoritmen forblir O (n).

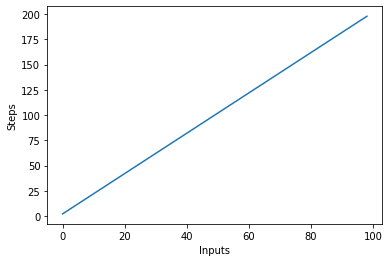
La oss visualisere denne nye algoritmen ved å plotte inngangene på X-aksen og antall trinn på Y-aksen:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

I manuset ovenfor kan du tydelig se det y=2n, men utgangen er lineær og ser slik ut:

Kvadratisk kompleksitet – O(n²)

Kompleksiteten til en algoritme sies å være kvadratisk når trinnene som kreves for å utføre en algoritme er en kvadratisk funksjon av antall elementer i inngangen. Kvadratisk kompleksitet er betegnet som O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Vi har en ytre sløyfe som itererer gjennom alle elementene i inndatalisten og deretter en nestet indre sløyfe, som igjen itererer gjennom alle elementene i inndatalisten. Det totale antallet utførte trinn er n*n, hvor n er antall elementer i inndatamatrisen.

Følgende graf plotter antall innganger mot trinnene for en algoritme med kvadratisk kompleksitet:

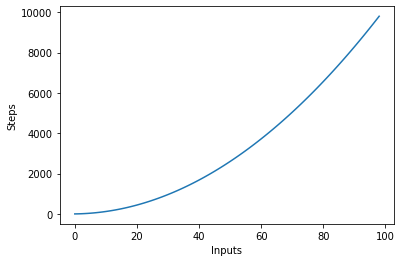
Logaritmisk kompleksitet – O (logn)

Noen algoritmer oppnår logaritmisk kompleksitet, som f.eks Binært søk. Binært søk søker etter et element i en matrise ved å merke av midten av en matrise, og beskjæring av halvdelen der elementet ikke er. Den gjør dette igjen for den gjenværende halvdelen, og fortsetter de samme trinnene til elementet er funnet. I hvert trinn, det halvdeler antall elementer i matrisen.

Dette krever at matrisen er sortert, og at vi gjør en antagelse om dataene (som at de er sortert).

Når du kan gjøre antagelser om innkommende data, kan du ta skritt som reduserer kompleksiteten til en algoritme. Logaritmisk kompleksitet er ønskelig, siden den oppnår god ytelse selv med høyt skalert input.

Finne kompleksiteten til komplekse funksjoner?

I tidligere eksempler hadde vi ganske enkle funksjoner på input. Men hvordan beregner vi Big-O av funksjoner som kaller (flere) andre funksjoner på inngangen?

La oss ta en titt:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

I skriptet ovenfor utføres flere oppgaver, først skrives en streng ut 5 ganger på konsollen ved å bruke print uttalelse. Deretter skriver vi ut inndatalisten to ganger på skjermen, og til slutt skrives en annen streng ut tre ganger på konsollen. For å finne kompleksiteten til en slik algoritme, må vi bryte ned algoritmekoden i deler og prøve å finne kompleksiteten til de enkelte brikkene. Merk ned kompleksiteten til hvert stykke.

I den første delen har vi:

for i in range(5):
	print("Python is awesome")

Kompleksiteten til denne delen er O (5) siden fem konstante trinn utføres i denne kodebiten uavhengig av inngangen.

Deretter har vi:

for item in items:
	print(item)

Vi vet kompleksiteten til kodestykket ovenfor er O (n). På samme måte er kompleksiteten til følgende kodestykke også O (n):

for item in items:
	print(item)

Til slutt, i den følgende kodebiten, skrives en streng ut tre ganger, derfor er kompleksiteten O (3):

print("Big O")
print("Big O")
print("Big O")

For å finne den generelle kompleksiteten, må vi ganske enkelt legge til disse individuelle kompleksitetene:

O(5) + O(n) + O(n) + O(3)

For å forenkle ovenstående får vi:

O(8) + O(2n) = O(8+2n)

Vi sa tidligere at når inngangen (som har lengde n i dette tilfellet) blir ekstremt stor, blir konstantene ubetydelige, dvs. to ganger eller halvparten av uendeligheten forblir fortsatt uendelig. Derfor kan vi ignorere konstantene. Den endelige kompleksiteten til algoritmen vil være O (n)!

Worst vs Best Case Complexity

Vanligvis, når noen spør deg om kompleksiteten til en algoritme - de er interessert i den verste tilfelle kompleksiteten (Big-O). Noen ganger kan de også være interessert i best-case-kompleksiteten (Big-Omega).

For å forstå forholdet mellom disse, la oss ta en titt på en annen kodebit:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

I skriptet ovenfor har vi en funksjon som tar et tall og en liste med tall som input. Det returnerer sant hvis det beståtte tallet finnes i listen over tall, ellers returnerer det None. Søker du på 2 i listen, vil den bli funnet i den første sammenligningen. Dette er best case-kompleksiteten til algoritmen ved at det søkte elementet finnes i den første søkte indeksen. Den beste sakskompleksiteten, i dette tilfellet, er O (1). På den annen side, hvis du søker 10, vil den bli funnet på den sist søkte indeksen. Algoritmen må derfor søke gjennom alle elementene i listen det verste tilfellet kompleksitet blir O (n).

I tillegg til best og worst case kompleksitet, kan du også beregne den gjennomsnittlige kompleksiteten (Big-Theta) av en algoritme, som forteller deg "gitt en tilfeldig inngang, hva er den forventede tidskompleksiteten til algoritmen"?

Romkompleksitet

I tillegg til tidskompleksiteten, hvor du teller antall trinn som kreves for å fullføre utførelsen av en algoritme, kan du også finne romkompleksitet som refererer til hvor mye plass du trenger å allokere i minnet under kjøringen av et program.

Ta en titt på følgende eksempel:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

De return_squares() funksjon aksepterer en liste over heltall og returnerer en liste med tilsvarende kvadrater. Algoritmen må allokere minne for samme antall elementer som i inndatalisten. Derfor blir romkompleksiteten til algoritmen O (n).

konklusjonen

Big-O-notasjonen er standardverdien som brukes til å måle kompleksiteten til en algoritme. I denne veiledningen studerte vi hva Big-O-notasjon er og hvordan den kan brukes til å måle kompleksiteten til en rekke algoritmer. Vi studerte også forskjellige typer Big-O-funksjoner ved hjelp av forskjellige Python-eksempler. Til slutt gjennomgikk vi kort den verste og beste sakskompleksiteten sammen med plasskompleksiteten.