Definitiv guide til logistisk regresjon i Python

Introduksjon

Noen ganger forvirret med lineær regresjon av nybegynnere – på grunn av deling av begrepet regresjon - logistisk regresjon er langt forskjellig fra lineær regresjon. Mens lineær regresjon forutsier verdier som 2, 2.45, 6.77 eller kontinuerlige verdier, gjør det til en regresjon algoritme, logistisk regresjon forutsier verdier som 0 eller 1, 1 eller 2 eller 3, som er diskrete verdier, gjør det til en klassifisering algoritme. Ja, det heter det regresjon men er en klassifisering algoritme. Mer om det om et øyeblikk.

Derfor, hvis datavitenskapsproblemet ditt involverer kontinuerlige verdier, kan du bruke en regresjon algoritme (lineær regresjon er en av dem). Ellers, hvis det involverer klassifisering av innganger, diskrete verdier eller klasser, kan du bruke en klassifisering algoritme (logistisk regresjon er en av dem).

I denne veiledningen skal vi utføre logistisk regresjon i Python med Scikit-Learn-biblioteket. Vi vil også forklare hvorfor ordet "regresjon" er tilstede i navnet og hvordan logistisk regresjon fungerer.

For å gjøre det, vil vi først laste inn data som vil bli klassifisert, visualisert og forhåndsbehandlet. Deretter vil vi bygge en logistisk regresjonsmodell som vil forstå disse dataene. Denne modellen vil deretter bli evaluert og brukt til å forutsi verdier basert på nye input.

Motivasjon

Firmaet du jobber for har samarbeidet med en tyrkisk landbruksgård. Dette partnerskapet innebærer salg av gresskarfrø. Gresskarfrø er veldig viktige for menneskelig ernæring. De inneholder en god andel karbohydrater, fett, protein, kalsium, kalium, fosfor, magnesium, jern og sink.

I datavitenskapsteamet er oppgaven din å se forskjellen mellom typene gresskarfrø bare ved å bruke data – eller klassifisering dataene i henhold til frøtype.

Den tyrkiske gården jobber med to gresskarfrøtyper, den ene heter Çerçevelik og den andre Ürgüp Sivrisi.

For å klassifisere gresskarfrøene har teamet ditt fulgt 2021-avisen "Bruk av maskinlæringsmetoder for klassifisering av gresskarfrø (Cucurbita pepo L.). Genetiske ressurser og avlingsutvikling" fra Koklu, Sarigil og Ozbek – i denne artikkelen er det en metodikk for å fotografere og trekke ut frømålingene fra bildene.

Etter å ha fullført prosessen beskrevet i papiret, ble følgende målinger hentet ut:

• Område – antall piksler innenfor grensene til et gresskarfrø
• Omkrets – omkretsen i piksler av et gresskarfrø
• Hovedaksens lengde – også omkretsen i piksler av et gresskarfrø
• Lengde på mindre akse – den lille akseavstanden til et gresskarfrø
• eksentrisitet – eksentrisiteten til et gresskarfrø
• Konveks område – antall piksler av det minste konvekse skallet i området som dannes av gresskarfrøet
• Utstrekning – forholdet mellom et gresskarfrøområde og avgrensningsrammepiklene
• Ekvivalent diameter – kvadratroten av multiplikasjonen av arealet til gresskarfrøet med fire delt på pi
• kompakthet – andelen av arealet til gresskarfrøet i forhold til arealet av sirkelen med samme omkrets
• soliditet – den konvekse og konvekse tilstanden til gresskarfrøene
• rundhet – ovaliteten til gresskarfrø uten å ta hensyn til forvrengninger i kantene
• Størrelsesforholdet – sideforholdet til gresskarfrøene

Det er målingene du må jobbe med. I tillegg til målene er det også Klasse etikett for de to typene gresskarkjerner.

For å begynne å klassifisere frøene, la oss importere dataene og begynne å se på dem.

Forstå datasettet

Etter å ha lastet ned datasettet, kan vi laste det inn i en datarammestruktur ved å bruke pandas bibliotek. Siden det er en excel-fil, vil vi bruke read_excel() metode:

import pandas as pd

fpath = 'dataset/pumpkin_seeds_dataset.xlsx' 
df = pd.read_excel(fpath)

Når dataene er lastet inn, kan vi ta en rask titt på de første 5 radene ved å bruke head() metode:

df.head() 

Dette resulterer i:

	Area 	Perimeter 	Major_Axis_Length 	Minor_Axis_Length 	Convex_Area 	Equiv_Diameter 	Eccentricity 	Solidity 	Extent 	Roundness 	Aspect_Ration 	Compactness 	Class
0 	56276 	888.242 	326.1485 			220.2388 			56831 			267.6805 		0.7376 			0.9902 		0.7453 	0.8963 		1.4809 			0.8207 			Çerçevelik
1 	76631 	1068.146 	417.1932 			234.2289 			77280 			312.3614 		0.8275 			0.9916 		0.7151 	0.8440 		1.7811 			0.7487 			Çerçevelik
2 	71623 	1082.987 	435.8328 			211.0457 			72663 			301.9822 		0.8749 			0.9857 		0.7400 	0.7674 		2.0651 			0.6929 			Çerçevelik
3 	66458 	992.051 	381.5638 			222.5322 			67118 			290.8899 		0.8123 			0.9902 		0.7396 	0.8486 		1.7146 			0.7624 			Çerçevelik
4 	66107 	998.146 	383.8883 			220.4545 			67117 			290.1207 		0.8187 			0.9850 		0.6752 	0.8338 		1.7413 			0.7557 			Çerçevelik

Her har vi alle målene i sine respektive kolonner, vår egenskaper, og også Klasse kolonne, vår mål, som er den siste i datarammen. Vi kan se hvor mange målinger vi har ved å bruke shape Egenskap:

df.shape 

Utgangen er:

(2500, 13)

Formresultatet forteller oss at det er 2500 oppføringer (eller rader) i datasettet og 13 kolonner. Siden vi vet at det er én målkolonne – betyr dette at vi har 12 funksjonskolonner.

Vi kan nå utforske målvariabelen, gresskarfrøet Class. Siden vi vil forutsi den variabelen, er det interessant å se hvor mange prøver av hvert gresskarfrø vi har. Vanligvis, jo mindre forskjellen er mellom antall forekomster i klassene våre, desto mer balansert er vårt utvalg og desto bedre spådommer.

Denne inspeksjonen kan gjøres ved å telle hver frøprøve med value_counts() metode:

df['Class'].value_counts() 

Koden ovenfor viser:

Çerçevelik       1300
Ürgüp Sivrisi    1200
Name: Class, dtype: int64

Vi kan se at det er 1300 prøver av Çerçevelik frø og 1200 prøver av Ürgüp Sivrisi frø. Legg merke til at forskjellen mellom dem er 100 prøver, en veldig liten forskjell, som er bra for oss og indikerer at det ikke er behov for å rebalansere antall prøver.

La oss også se på den beskrivende statistikken over funksjonene våre med describe() metode for å se hvor godt distribuert dataene er. Vi vil også transponere den resulterende tabellen med T for å gjøre det enklere å sammenligne på tvers av statistikk:

df.describe().T

Den resulterende tabellen er:

					count 	mean 			std 			min 		25% 			50% 			75% 			max
Area 				2500.0 	80658.220800 	13664.510228 	47939.0000 	70765.000000 	79076.00000 	89757.500000 	136574.0000
Perimeter 			2500.0 	1130.279015 	109.256418 		868.4850 	1048.829750 	1123.67200 		1203.340500 	1559.4500
Major_Axis_Length 	2500.0 	456.601840 		56.235704 		320.8446 	414.957850 		449.49660 		492.737650 		661.9113
Minor_Axis_Length 	2500.0 	225.794921 		23.297245 		152.1718 	211.245925 		224.70310 		240.672875 		305.8180
Convex_Area 		2500.0 	81508.084400 	13764.092788 	48366.0000 	71512.000000 	79872.00000 	90797.750000 	138384.0000
Equiv_Diameter 		2500.0 	319.334230 		26.891920 		247.0584 	300.167975 		317.30535 		338.057375 		417.0029
Eccentricity 		2500.0 	0.860879 		0.045167 		0.4921 		0.831700 		0.86370 		0.897025 		0.9481
Solidity 			2500.0 	0.989492 		0.003494 		0.9186 		0.988300 		0.99030 		0.991500 		0.9944
Extent 				2500.0 	0.693205 		0.060914 		0.4680 		0.658900 		0.71305 		0.740225 		0.8296
Roundness 			2500.0 	0.791533 		0.055924 		0.5546 		0.751900 		0.79775 		0.834325 		0.9396
Aspect_Ration 		2500.0 	2.041702 		0.315997 		1.1487 		1.801050 		1.98420 		2.262075 		3.1444
Compactness 		2500.0 	0.704121 		0.053067 		0.5608 		0.663475 		0.70770 		0.743500 		0.9049

Ved å se på tabellen, når du sammenligner bety og standardavvik (std) kolonner, kan man se at de fleste funksjoner har et gjennomsnitt som er langt fra standardavviket. Det indikerer at dataverdiene ikke er konsentrert rundt middelverdien, men mer spredt rundt den – med andre ord, de har høy variasjon.

Også når man ser på minimum (min) Og maksimal (max) kolonner, noen funksjoner, som f.eks Areaog Convex_Area, har store forskjeller mellom minimums- og maksimumsverdier. Dette betyr at disse kolonnene har svært små data og også svært store dataverdier, eller høyere amplitude mellom dataverdier.

Med høy variabilitet, høy amplitude og funksjoner med forskjellige måleenheter, vil de fleste av våre data dra nytte av å ha samme skala for alle funksjoner eller være skalert. Dataskalering vil sentrere data rundt gjennomsnittet og redusere variansen.

Dette scenariet indikerer sannsynligvis også at det er uteliggere og ekstreme verdier i data. Så det er best å ha noen avvikende behandling i tillegg til å skalere dataene.

Det er noen maskinlæringsalgoritmer, for eksempel trebaserte algoritmer som Tilfeldig skogklassifisering, som ikke påvirkes av høy datavarians, uteliggere og ekstreme verdier. Logistisk regresjon er annerledes, er den basert på en funksjon som kategoriserer verdiene våre, og parametrene til den funksjonen kan påvirkes av verdier som er utenfor den generelle datatrenden og har høy varians.

Vi vil forstå mer om logistisk regresjon om litt når vi får implementert det. Foreløpig kan vi fortsette å utforske dataene våre.

Visualisere dataene

Frem til nå, med den beskrivende statistikken, har vi et noe abstrakt øyeblikksbilde av noen kvaliteter ved dataene. Et annet viktig skritt er å visualisere det og bekrefte hypotesen vår om høy varians, amplitude og uteliggere. For å se om det vi har observert så langt viser seg i dataene, kan vi plotte noen grafer.

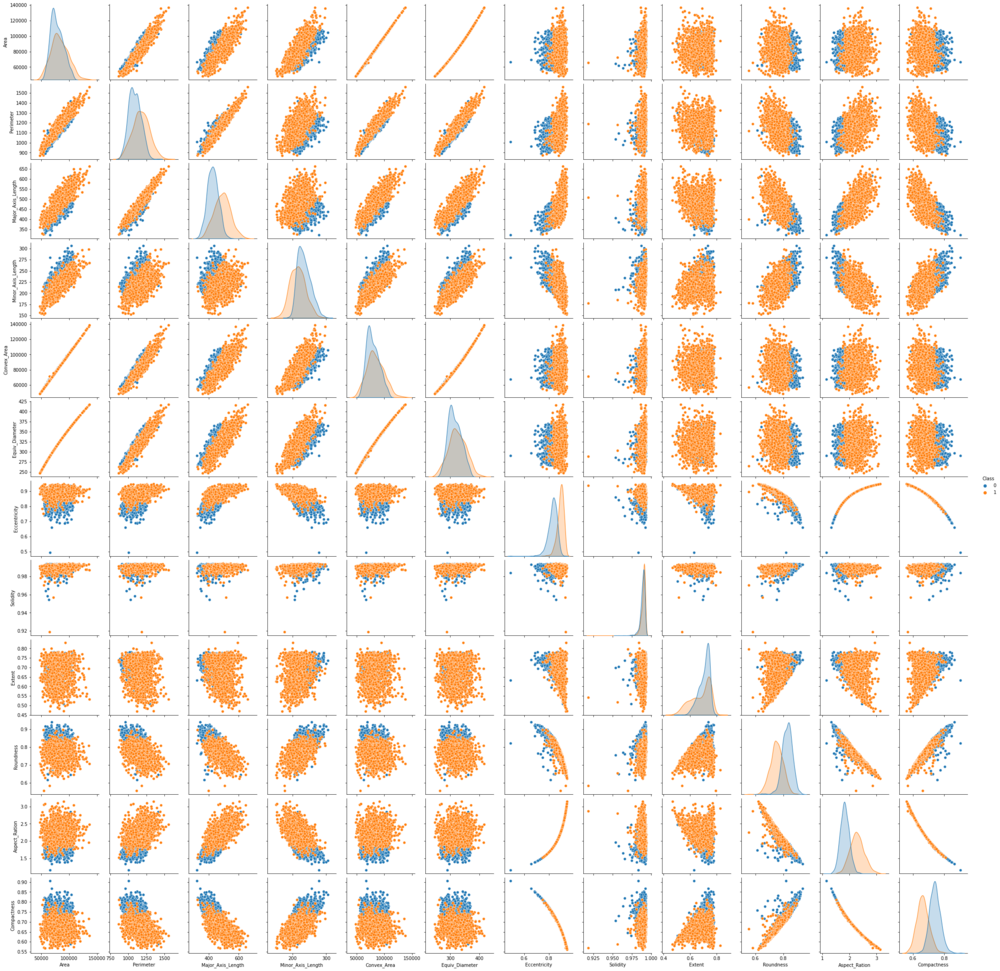
Det er også interessant å se hvordan funksjonene forholder seg til de to klassene som vil bli spådd. For å gjøre det, la oss importere seaborn pakke og bruke pairplot graf for å se på hver funksjonsfordeling, og hver klasseseparasjon per funksjon:

import seaborn as sns


sns.pairplot(data=df, hue='Class')

Når vi ser på parplotten, kan vi se at i de fleste tilfeller punktene til Çerçevelik klasse er tydelig atskilt fra poengene til Ürgüp Sivrisi klasse. Enten er poengene til en klasse til høyre når de andre er til venstre, eller noen er opp mens de andre er nede. Hvis vi skulle bruke en slags kurve eller linje for å skille klasser, viser dette at det er lettere å skille dem, hvis de var blandet, ville klassifisering vært en vanskeligere oppgave.

på Eccentricity, Compactness og Aspect_Ration kolonner, noen punkter som er "isolert" eller avviker fra den generelle datatrenden - uteliggere - er også lett å oppdage.

Når du ser på diagonalen fra øvre venstre til nederst til høyre i diagrammet, legg merke til at datafordelingene også er fargekodet i henhold til våre klasser. Fordelingsformene og avstanden mellom begge kurvene er andre indikatorer på hvor separerbare de er – jo lenger fra hverandre, jo bedre. I de fleste tilfeller er de ikke lagt over hverandre, noe som betyr at de er lettere å skille, noe som også bidrar til vår oppgave.

I rekkefølge kan vi også plotte boksplottene til alle variabler med sns.boxplot() metode. De fleste ganger er det nyttig å orientere boksplottene horisontalt, så formene til boksplottene er de samme som distribusjonsformene, vi kan gjøre det med orient argument:

sns.boxplot(data=df, orient='h') 

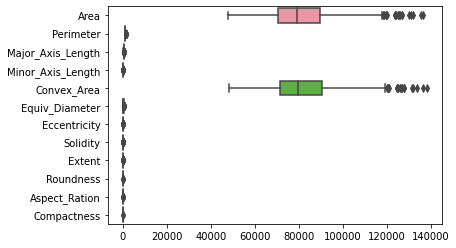
Legg merke til det i plottet ovenfor Area og Convex_Area har en så høy størrelse sammenlignet med størrelsen på de andre kolonnene, at de klemmer de andre boksplottene. For å kunne se på alle boxplot kan vi skalere funksjonene og plotte dem på nytt.

Før vi gjør det, la oss bare forstå at hvis det er verdier av funksjoner som er nært knyttet til andre verdier, for eksempel – hvis det er verdier som også blir større når andre funksjonsverdier blir større, har en positiv korrelasjon; eller hvis det er verdier som gjør det motsatte, blir mindre mens andre verdier blir mindre, med en negativ korrelasjon.

Dette er viktig å se på fordi det å ha sterke relasjoner i data kan bety at noen kolonner ble avledet fra andre kolonner eller har en lignende betydning som vår modell. Når det skjer, kan modellresultatene bli overvurdert, og vi ønsker resultater som er nærmere virkeligheten. Hvis det er sterke korrelasjoner, betyr det også at vi kan redusere antall funksjoner, og bruke færre kolonner som gjør modellen mer parsimonious.

La oss ta en titt på korrelasjonene mellom variabler, og så kan vi gå videre til å forhåndsbehandle dataene. Vi vil beregne korrelasjonene med corr() metode og visualiser dem med Seaborn's heatmap(). Standardstørrelsen på varmekartet har en tendens til å være liten, så vi vil importere matplotlib (generell visualiseringsmotor/bibliotek som Seaborn er bygget på toppen av) og endre størrelsen med figsize:

import matplotlib.pyplot as plt
plt.figure(figsize=(15, 10))

correlations = df.corr()
sns.heatmap(correlations, annot=True) 

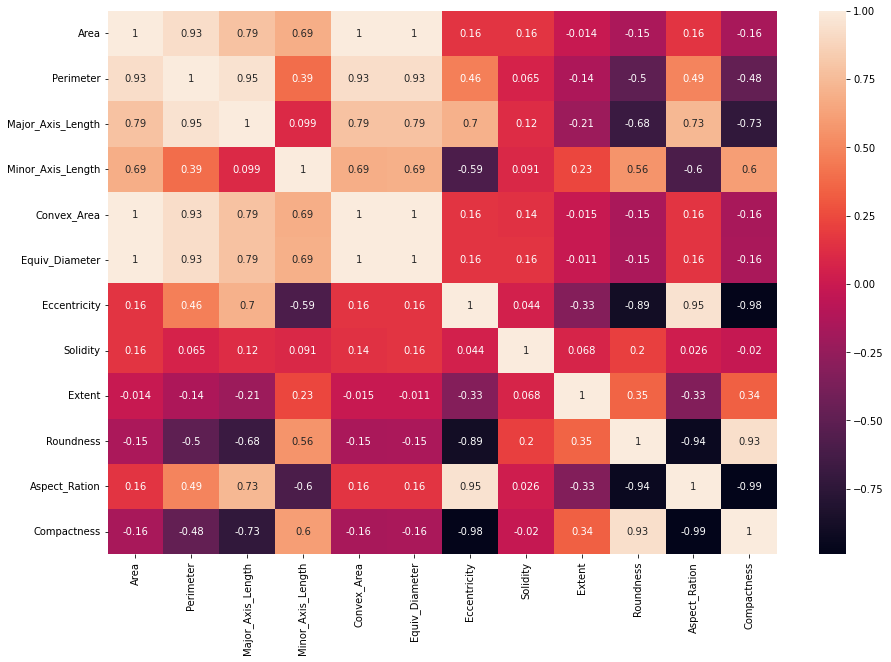
I dette varmekartet er verdiene nærmere 1 eller -1 verdiene vi må ta hensyn til. Det første tilfellet angir en høy positiv korrelasjon og det andre, en høy negativ korrelasjon. Begge verdiene, hvis ikke over 0.8 eller -0.8 vil være fordelaktige for vår logistiske regresjonsmodell.

Når det er høye korrelasjoner som den av 0.99 mellom Aspec_Ration og Compactness, betyr dette at vi kan velge å kun bruke Aspec_Ration eller bare Compactness, i stedet for begge (siden de er nesten like prediktorer av hverandre). Det samme gjelder for Eccentricity og Compactness med en -0.98 korrelasjon, for Area og Perimeter med en 0.94 korrelasjon og noen andre kolonner.

Forhåndsbehandling av dataene

Siden vi allerede har utforsket dataene en stund, kan vi begynne å forhåndsbehandle dem. For nå, la oss bruke alle funksjonene for klasseprediksjonen. Etter å ha oppnådd en første modell, en grunnlinje, kan vi fjerne noen av de høyt korrelerte kolonnene og sammenligne den med grunnlinjen.

Innslagskolonnene vil være vår X data og klassekolonnen, vår y måldata:

y = df['Class']
X = df.drop(columns=['Class'], axis=1)

Gjør om kategoriske funksjoner til numeriske funksjoner

Angående vår Class kolonne – verdiene er ikke tall, dette betyr at vi også må transformere dem. Det er mange måter å gjøre denne transformasjonen på; her vil vi bruke replace() metode og erstatte Çerçevelik til 0 og Ürgüp Sivrisi til 1.

y = y.replace('Çerçevelik', 0).replace('Ürgüp Sivrisi', 1)

Ha kartleggingen i bakhodet! Når du leser resultater fra modellen din, vil du i det minste konvertere disse tilbake i tankene dine, eller tilbake til klassenavnet for andre brukere.

Dele inn data i tog- og testsett

I vår utforskning har vi lagt merke til at funksjonene trengte skalering. Hvis vi gjorde skaleringen nå, eller på en automatisk måte, ville vi skalert verdier med hele X og y. I så fall ville vi introdusert datalekkasje, ettersom verdiene til det snart kommende testsettet ville ha påvirket skaleringen. Datalekkasje er en vanlig årsak til irreproduserbare resultater og illusorisk høy ytelse for ML-modeller.

Å tenke på skaleringen viser at vi først må splitte X og y data videre inn i tog- og testsett og deretter til passer en scaler på treningssettet, og til forvandle både toget og testsettene (uten at testsettet noen gang påvirker skaleren som gjør dette). Til dette vil vi bruke Scikit-Learn's train_test_split() metode:

from sklearn.model_selection import train_test_split
SEED = 42 

X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size=.25, 
                                                    random_state=SEED)

Stille test_size=.25 sikrer at vi bruker 25 % av dataene til testing og 75 % til trening. Dette kan utelates når det først er standarddelingen, men Pytonisk måte å skrive kode på anbefaler at det å være "eksplisitt er bedre enn implisitt".

Etter å ha delt opp dataene i tog- og testsett, er det en god praksis å se på hvor mange poster som er i hvert sett. Det kan gjøres med shape Egenskap:

X_train.shape, X_test.shape, y_train.shape, y_test.shape

Dette viser:

((1875, 12), (625, 12), (1875,), (625,))

Vi kan se at etter splittelsen har vi 1875 rekorder for trening og 625 for testing.

Skalering av data

Når vi har våre tog- og testsett klare, kan vi fortsette å skalere dataene med Scikit-Learn StandardScaler objekt (eller andre skalere levert av biblioteket). For å unngå lekkasje, er scaler montert på X_train data og togverdier brukes deretter til å skalere – eller transformere – både tog- og testdata:

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Siden du vanligvis ringer:

scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

De to første linjene kan kollapses med entall fit_transform() call, som passer til scaler på settet, og forvandler den på én gang. Vi kan nå reprodusere boksplott-grafene for å se forskjellen etter skalering av data.

Med tanke på at skaleringen fjerner kolonnenavn, kan vi før plotting organisere togdata i en dataramme med kolonnenavn igjen for å lette visualiseringen:

column_names = df.columns[:12] 
X_train = pd.DataFrame(X_train, columns=column_names)

sns.boxplot(data=X_train, orient='h')

Vi kan endelig se alle boxplottene våre! Legg merke til at alle av dem har uteliggere, og funksjonene som presenterer en fordeling lenger fra normalen (som har kurver enten skjevt til venstre eller høyre), som f.eks. Solidity, Extent, Aspect_Rationog Compactedness, er de samme som hadde høyere korrelasjoner.

Fjerne uteliggere med IQR-metoden

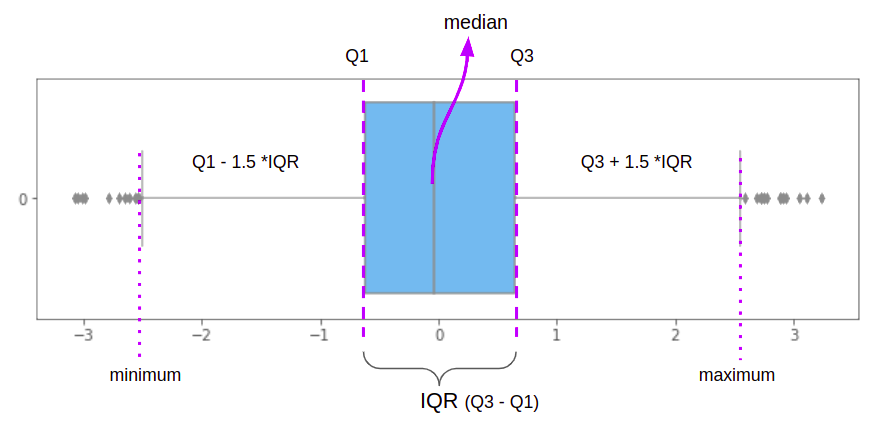
Vi vet allerede at logistisk regresjon kan påvirkes av uteliggere. En av måtene å behandle dem på er å bruke en metode som heter Interkvartil rekkevidde or I.Q.R.. Det første trinnet i IQR-metoden er å dele opp togdataene våre i fire deler, kalt kvartiler. Den første kvartilen, Q1, utgjør 25 % av dataene, den andre, Q2, til 50 %, den tredje, Q3, til 75 %, og den siste, Q4, til 100 %. Boksene i boksplotten er definert av IQR-metoden og er en visuell representasjon av den.

Med tanke på et horisontalt boksplott, markerer den vertikale linjen til venstre 25 % av dataene, den vertikale linjen i midten, 50 % av dataene (eller medianen), og den siste vertikale linjen til høyre, 75 % av dataene . Jo jevnere i størrelse begge firkantene definert av de vertikale linjene er – eller jo mer den vertikale medianlinjen er i midten – betyr at dataene våre er nærmere normalfordelingen eller mindre skjeve, noe som er nyttig for vår analyse.

Foruten IQR-boksen, er det også horisontale linjer på begge sider av den. Disse linjene markerer minimums- og maksimumsfordelingsverdiene definert av

$$
Minimum = Q1 – 1.5*IQR
$$

og

$$
Maksimum = Q3 + 1.5*IQR
$$

IQR er nøyaktig forskjellen mellom Q3 og Q1 (eller Q3 – Q1), og det er det mest sentrale punktet for data. Det er grunnen til at når vi finner IQR, ender vi opp med å filtrere uteliggere i dataekstremitetene, eller i minimums- og maksimumspoengene. Boksplott gir oss en sniktitt på hva resultatet av IQR-metoden blir.

Vi kan bruke pandaer quantile() metode for å finne våre kvantiler, og iqr fra scipy.stats pakke for å få det interkvartile dataområdet for hver kolonne:

from scipy.stats import iqr

Q1 = X_train.quantile(q=.25)
Q3 = X_train.quantile(q=.75)

IQR = X_train.apply(iqr)

Nå har vi Q1, Q3 og IQR, vi kan filtrere ut verdiene nærmere medianen:

minimum = X_train < (Q1-1.5*IQR)
maximum = X_train > (Q3+1.5*IQR)


filter = ~(minimum | maximum).any(axis=1)


X_train = X_train[filter]

Etter å ha filtrert treningsradene våre, kan vi se hvor mange av dem som fortsatt er i dataene med shape:

X_train.shape

Dette resulterer i:

(1714, 12)

Vi kan se at antall rader gikk fra 1875 til 1714 etter filtrering. Dette betyr at 161 rader inneholdt uteliggere eller 8.5 % av dataene.

Etter å ha fjernet uteliggere er vi nesten klare til å inkludere data i modellen. For modelltilpasningen vil vi bruke togdata. X_train er filtrert, men hva med y_train?

y_train.shape

Dette gir utganger:

(1875,)

Legg merke til det y_train har fortsatt 1875 rader. Vi må matche antallet y_train rader til antall X_train rader og ikke bare vilkårlig. Vi må fjerne y-verdiene for forekomstene av gresskarfrø som vi fjernet, som sannsynligvis er spredt gjennom y_train sett. Den filtrerte X_train stil har sine originale indekser og indeksen har hull der vi fjernet uteliggere! Vi kan da bruke indeksen til X_train DataFrame for å søke etter de tilsvarende verdiene i y_train:

y_train = y_train.iloc[X_train.index]

Etter å ha gjort det, kan vi se på y_train form igjen:

y_train.shape

Hvilke utganger:

(1714,)

Nå, y_train har også 1714 rader og de er de samme som X_train rader. Vi er endelig klare til å lage vår logistiske regresjonsmodell!

Implementering av den logistiske regresjonsmodellen

Den vanskelige delen er unnagjort! Forbehandling er vanligvis vanskeligere enn modellutvikling, når det gjelder å bruke biblioteker som Scikit-Learn, som har strømlinjeformet bruken av ML-modeller til bare et par linjer.

Først importerer vi LogisticRegression klasse og instansiere den, lage en LogisticRegression gjenstand:

from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(random_state=SEED)

For det andre tilpasser vi togdataene våre til logreg modell med fit() metoden, og forutsi våre testdata med predict() metode, lagring av resultatene som y_pred:

logreg.fit(X_train.values, y_train)
y_pred = logreg.predict(X_test)

Vi har allerede laget spådommer med modellen vår! La oss se på de første 3 radene X_train for å se hvilke data vi har brukt:

X_train[:3]

Koden ovenfor gir ut:

       Area          Perimeter     Major_Axis_Length    Minor_Axis_Length    Convex_Area   Equiv_Diameter       Eccentricity  Solidity      Extent        Roundness     Aspect_Ration        Compactness
0      -1.098308     -0.936518     -0.607941            -1.132551            -1.082768     -1.122359            0.458911      -1.078259     0.562847      -0.176041     0.236617             -0.360134
1      -0.501526     -0.468936     -0.387303            -0.376176            -0.507652     -0.475015            0.125764      0.258195      0.211703      0.094213      -0.122270            0.019480
2      0.012372      -0.209168     -0.354107            0.465095              0.003871      0.054384            -0.453911     0.432515      0.794735      0.647084      -0.617427            0.571137

Og ved de første 3 spådommene i y_pred for å se resultatene:

y_pred[:3] 

Dette resulterer i:

array([0, 0, 0])

For de tre radene var våre spådommer at de var frø av første klasse, Çerçevelik.

Med logistisk regresjon, i stedet for å forutsi den endelige klassen, som f.eks 0, kan vi også forutsi sannsynligheten raden har for å tilhøre 0 klasse. Dette er hva som faktisk skjer når logistisk regresjon klassifiserer data, og predict() metoden sender deretter denne prediksjonen gjennom en terskel for å returnere en "hard" klasse. For å forutsi sannsynligheten for å tilhøre en klasse, predict_proba() benyttes:

y_pred_proba = logreg.predict_proba(X_test)

La oss også ta en titt på de tre første verdiene av y-sannsynlighetsprediksjonene:

y_pred_proba[:3] 

Hvilke utganger:

        # class 0   class 1   
array([[0.54726628, 0.45273372],
       [0.56324527, 0.43675473],
       [0.86233349, 0.13766651]])

Nå, i stedet for tre nuller, har vi én kolonne for hver klasse. I kolonnen til venstre begynner med 0.54726628, er sannsynlighetene for dataene som gjelder klassen 0; og i høyre kolonne, starter med 0.45273372, er sannsynligheten for at det gjelder klassen 1.

Det er mer informasjon om hvordan den anslåtte utgangen ble laget. Det var det faktisk ikke 0, men en 55% sjanse for klasse 0, og en 45% sjanse for klasse 1. Dette viser hvordan de tre første X_test datapunkter, knyttet til klasse 0, er egentlig klare bare når det gjelder det tredje datapunktet, med 86 % sannsynlighet – og ikke så mye for de to første datapunktene.

Når du kommuniserer funn ved hjelp av ML-metoder – er det vanligvis best å returnere en myk klasse, og den tilhørende sannsynligheten som "tillit" av den klassifiseringen.

Vi vil snakke mer om hvordan det beregnes når vi går dypere inn i modellen. På dette tidspunktet kan vi gå videre til neste trinn.

Evaluering av modellen med klassifiseringsrapporter

Det tredje trinnet er å se hvordan modellen presterer på testdata. Vi kan importere Scikit-Learn classification_report() og passere vår y_test og y_pred som argumenter. Etter det kan vi skrive ut svaret.

Klassifiseringsrapporten inneholder de mest brukte klassifiseringsmetrikkene, som f.eks presisjon, husker, f1-scoreog nøyaktighet.

1. Precision: for å forstå hvilke korrekte prediksjonsverdier som ble ansett som riktige av klassifisereren vår. Presisjon vil dele de sanne positive verdiene med alt som ble spådd som positivt:

$$
presisjon = frac{tekst{sann positiv}}{tekst{sann positiv} + tekst{falsk positiv}}
$$

2. Husker: for å forstå hvor mange av de sanne positive som ble identifisert av klassifisereren vår. Tilbakekallingen beregnes ved å dele de sanne positive med alt som burde vært spådd som positivt:

$$
tilbakekall = frac{tekst{sann positiv}}{tekst{sann positiv} + tekst{falsk negativ}}
$$

3. F1-poengsum: er den balanserte eller harmonisk middel av presisjon og tilbakekalling. Den laveste verdien er 0 og den høyeste er 1. Når f1-score er lik 1, betyr det at alle klasser ble riktig spådd – dette er en veldig vanskelig poengsum å oppnå med ekte data:

$$
tekst{f1-score} = 2* frac{tekst{presisjon} * tekst{recall}}{tekst{precision} + tekst{recall}}
$$

4. Nøyaktighet: beskriver hvor mange spådommer klassifiseringen vår fikk riktige. Den laveste nøyaktighetsverdien er 0 og den høyeste er 1. Denne verdien multipliseres vanligvis med 100 for å få en prosentandel:

$$
nøyaktighet = frac{tekst{antall korrekte spådommer}}{tekst{totalt antall spådommer}}
$$

from sklearn.metrics import classification_report
cr = classification_report(y_test, y_pred)
print(cr)

Vi kan deretter se på klassifiseringsrapporten:

				precision    recall  f1-score   support

           0       0.83      0.91      0.87       316
           1       0.90      0.81      0.85       309

    accuracy                           0.86       625
   macro avg       0.86      0.86      0.86       625
weighted avg       0.86      0.86      0.86       625

Dette er vårt resultat. Legg merke til det precision, recall, f1-scoreog accuracy alle beregningene er veldig høye, over 80 %, noe som er ideelt – men disse resultatene ble sannsynligvis påvirket av høye korrelasjoner, og vil ikke opprettholdes i det lange løp.

Modellens nøyaktighet er 86 %, noe som betyr at den får klassifiseringen feil 14 % av gangene. Vi har den generelle informasjonen, men det ville vært interessant å vite om de 14 % feilene skjer angående klassifiseringen av klasse 0 eller klasse 1. For å identifisere hvilke klasser som er feilidentifisert som hvilke, og i hvilken frekvens – kan vi beregne og plotte en forvirringsmatrise av modellens spådommer.

Evaluering av modellen med en forvirringsmatrise

La oss beregne og plotte forvirringsmatrisen. Etter å ha gjort det, kan vi forstå hver del av det. For å plotte forvirringsmatrisen bruker vi Scikit-Learn confusion_matrix(), som vi importerer fra metrics modul.

Forvirringsmatrisen er lettere å visualisere med en Seaborn heatmap(). Så, etter å ha generert den, vil vi sende forvirringsmatrisen vår som et argument for varmekartet:

from sklearn.metrics import confusion_matrix

cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d')

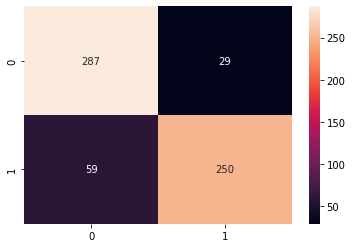
5. Forvirringsmatrise: matrisen viser hvor mange prøver modellen fikk riktig eller feil for hver klasse. Verdiene som var korrekte og korrekt forutsagt kalles ekte positive, og de som ble spådd som positive, men som ikke var positive, kalles falske positive. Den samme nomenklaturen til ekte negativer og falske negativer brukes for negative verdier;

Ved å se på forvirringsmatriseplottet kan vi se at vi har 287 verdier som var 0 og spådd som 0 - eller ekte positive for klassen 0 (Cerçevelik-frøene). Vi har også 250 sanne positive ting for klassen 1 (Ürgüp Sivrisi frø). De sanne positive er alltid plassert i matrisediagonalen som går fra øvre venstre til nedre høyre.

Vi har også 29 verdier som skulle være 0, men spådd som 1 (falske positive) Og 59 verdier som var 1 og spådd som 0 (falske negativer). Med disse tallene kan vi forstå at feilen som modellen gjør mest er at den forutsier falske negativer. Så det kan stort sett ende opp med å klassifisere et Ürgüp Sivrisi-frø som et Çerçevelik-frø.

Denne typen feil forklares også av 81% tilbakekalling av klassen 1. Legg merke til at beregningene er koblet sammen. Og forskjellen i tilbakekallingen kommer fra å ha 100 færre prøver av Ürgüp Sivrisi-klassen. Dette er en av konsekvensene av å ha bare noen få prøver mindre enn den andre klassen. For å forbedre tilbakekallingen ytterligere kan du enten eksperimentere med klassevekter eller bruke flere Ürgüp Sivrisi-prøver.

Så langt har vi utført de fleste av de tradisjonelle datavitenskapelige trinnene og brukt den logistiske regresjonsmodellen som en svart boks.

Nå er det på tide å åpne den svarte boksen og se inn i den, for å gå dypere inn i å forstå hvordan logistisk regresjon fungerer.

Gå dypere inn i hvordan logistisk regresjon virkelig fungerer

De regresjon Ordet er ikke der ved en tilfeldighet, for å forstå hva logistisk regresjon gjør, kan vi huske hva dens søsken, lineær regresjon gjør med dataene. Den lineære regresjonsformelen var følgende:

$$
y = b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n
$$

I hvilken b₀ var regresjonsavskjæringen, b¹ koeffisienten og x¹ dataen.

Den ligningen resulterte i en rett linje som ble brukt til å forutsi nye verdier. Når vi minner om introduksjonen, er forskjellen nå at vi ikke vil forutsi nye verdier, men en klasse. Så den rette linjen må endres. Med logistisk regresjon introduserer vi en ikke-linearitet og prediksjonen gjøres nå ved å bruke en kurve i stedet for en linje:

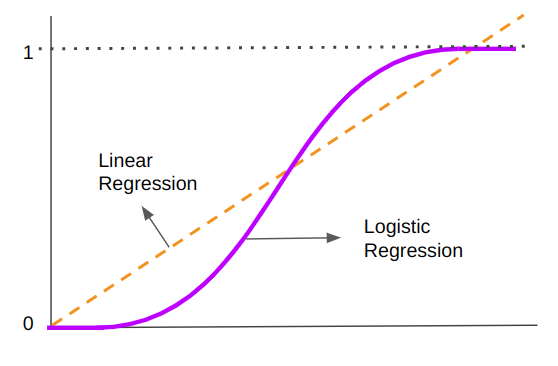
Legg merke til at mens den lineære regresjonslinjen fortsetter og er laget av kontinuerlige uendelige verdier, kan den logistiske regresjonskurven deles på midten og har ytterpunkter i 0 og 1 verdier. Den "S"-formen er grunnen til at den klassifiserer data – punktene som er nærmere eller faller på den høyeste ekstremiteten tilhører klasse 1, mens punktene som er i nedre kvadrant eller nærmere 0, tilhører klasse 0. Midten av "S" er midten mellom 0 og 1, 0.5 - det er terskelen for de logistiske regresjonspunktene.

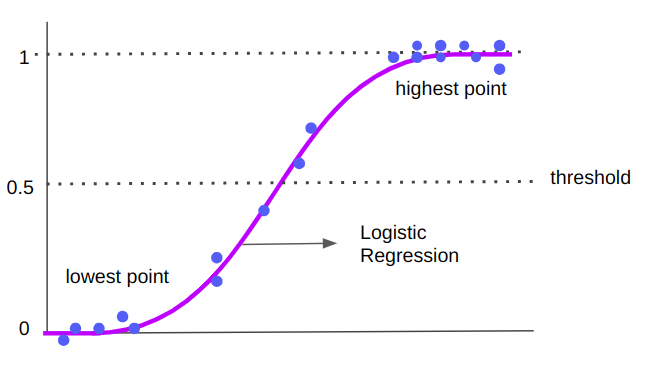
Vi forstår allerede den visuelle forskjellen mellom logistisk og lineær regresjon, men hva med formelen? Formelen for logistisk regresjon er følgende:

$$
y = b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n
$$

Det kan også skrives som:

$$
y_{prob} = frac{1}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}
$$

Eller til og med skrives som:

$$
y_{prob} = frac{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3)_n x_n x_n
$$

I ligningen ovenfor har vi sannsynligheten for input, i stedet for verdien. Den har 1 som teller, så den kan resultere i en verdi mellom 0 og 1, og 1 pluss en verdi i nevneren, slik at verdien er 1 og noe – dette betyr at hele brøkresultatet ikke kan være større enn 1 .

Og hva er verdien som er i nevneren? Det er e, basen til den naturlige logaritmen (omtrent 2.718282), hevet til kraften til lineær regresjon:

$$
e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}
$$

En annen måte å skrive det på er:

$$
ln venstre (frac{p}{1-p} høyre) = {(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}
$$

I den siste ligningen, ln er den naturlige logaritmen (grunntall e) og p er sannsynligheten, så logaritmen for sannsynligheten for resultatet er den samme som det lineære regresjonsresultatet.

Med andre ord, med det lineære regresjonsresultatet og den naturlige logaritmen, kan vi komme frem til sannsynligheten for at en inngang hører til eller ikke til en designet klasse.

Hele den logistiske regresjonsavledningsprosessen er som følger:

$$
p{X} = frac{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n x_n)}}
$$

$$
p(1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}) = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + ldots + b)_}n * x_
$$

$$
p + p*e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)} = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + ldots + b_n * x_n)}
$$

p
=

e

(

b
0

+

b
1

*

x
1

+

b
2

*

x
2

+

b
3

*

x
3

+
...
+

b
n

*

x
n

)

-
p
*

e

(

b
0

+

b
1

*

x
1

+

b
2

*

x
2

+

b
3

*

x
3

+
...
+

b
n

*

x
n

)

$$
frac{p}{1-p} = e^{(b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + ldots + b_n * x_n)}
$$

$$
ln venstre( frac{p}{1-p} høyre) = (b_0 + b_1 * x_1 + b_2 *x_2 + b_3 * x_3 + ldots + b_n * x_n)
$$

Dette betyr at den logistiske regresjonsmodellen også har koeffisienter og en avskjæringsverdi. Fordi den bruker en lineær regresjon og legger til en ikke-lineær komponent til den med den naturlige logaritmen (e).

Vi kan se verdiene til koeffisientene og skjæringspunktet til modellen vår, på samme måte som vi gjorde for lineær regresjon, ved å bruke coef_ og intercept_ eiendommer:

logreg.coef_

Som viser koeffisientene til hver av de 12 funksjonene:

array([[ 1.43726172, -1.03136968,  0.24099522, -0.61180768,  1.36538261,
        -1.45321951, -1.22826034,  0.98766966,  0.0438686 , -0.78687889,
         1.9601197 , -1.77226097]])

logreg.intercept_

Det resulterer i:

array([0.08735782])

Med koeffisientene og avskjæringsverdiene kan vi beregne de predikerte sannsynlighetene for dataene våre. La oss ta den første X_test verdier igjen, som et eksempel:

X_test[:1]

Dette returnerer den første raden av X_test som en NumPy-matrise:

array([[-1.09830823, -0.93651823, -0.60794138, -1.13255059, -1.0827684 ,
        -1.12235877,  0.45891056, -1.07825898,  0.56284738, -0.17604099,
         0.23661678, -0.36013424]])

Etter den innledende ligningen:

$$
p{X} = frac{e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n * x_n)}}{1 + e^{(b_0 + b_1 * x_1 + b_2 * x_2 + b_3 * x_3 + ldots + b_n x_n)}}
$$

I python har vi:

import math

lin_reg = logreg.intercept_[0] + 
((logreg.coef_[0][0]* X_test[:1][0][0])+ 
(logreg.coef_[0][1]* X_test[:1][0][1])+ 
(logreg.coef_[0][2]* X_test[:1][0][2])+ 
(logreg.coef_[0][3]* X_test[:1][0][3])+ 
(logreg.coef_[0][4]* X_test[:1][0][4])+ 
(logreg.coef_[0][5]* X_test[:1][0][5])+ 
(logreg.coef_[0][6]* X_test[:1][0][6])+ 
(logreg.coef_[0][7]* X_test[:1][0][7])+ 
(logreg.coef_[0][8]* X_test[:1][0][8])+ 
(logreg.coef_[0][9]* X_test[:1][0][9])+ 
(logreg.coef_[0][10]* X_test[:1][0][10])+ 
(logreg.coef_[0][11]* X_test[:1][0][11]))

px = math.exp(lin_reg)/(1 +(math.exp(lin_reg)))
px

Dette resulterer i:

0.45273372469369133

Hvis vi ser på igjen predict_proba resultatet av den første X_test linje, vi har:

logreg.predict_proba(X_test[:1])

Dette betyr at den opprinnelige logistiske regresjonsligningen gir oss sannsynligheten for input angående klasse 1, for å finne ut hvilken sannsynlighet som er for klassen 0, kan vi ganske enkelt:

1 - px

Legg merke til at begge deler px og 1-px er identiske med predict_proba resultater. Slik beregnes logistisk regresjon og hvorfor regresjon er en del av navnet. Men hva med begrepet logis?

Begrepet logis kommer fra logit, som er en funksjon vi allerede har sett:

$$
l venstre (frac{p}{1-p} høyre)
$$

Vi har akkurat regnet det med px og 1-px. Dette er logit, også kalt log-oddser siden det er lik logaritmen til oddsen hvor p er en sannsynlighet.

konklusjonen

I denne guiden har vi studert en av de mest grunnleggende maskinlæringsklassifiseringsalgoritmene, dvs logistisk regresjon.

I utgangspunktet implementerte vi logistisk regresjon som en svart boks med Scikit-Learns maskinlæringsbibliotek, og senere forsto vi det steg for steg for å ha et klart hvorfor og hvor begrepene regresjon og logistikk kommer fra.

Vi har også utforsket og studert dataene, og forstår at det er en av de mest avgjørende delene av en datavitenskapelig analyse.

Herfra vil jeg råde deg til å leke med multiklasse logistisk regresjon, logistisk regresjon for mer enn to klasser – du kan bruke den samme logistiske regresjonsalgoritmen for andre datasett som har flere klasser, og tolke resultatene.

Jeg vil også råde deg til å studere L1 og L2 regulariseringer, de er en måte å "straffe" de høyere dataene for at de skal bli nærmere normalen, og holder ut modellens kompleksitet, slik at algoritmen kan få et bedre resultat. Scikit-Learn-implementeringen vi brukte, har allerede L2-regularisering som standard. En annen ting å se på er det annerledes løsere, Eksempel lbgs, som optimaliserer ytelsen til logistisk regresjonsalgoritme.

Det er også viktig å ta en titt på statistisk tilnærming til logistisk regresjon. Det har antagelser om oppførselen til data, og om annen statistikk som må holdes for å garantere tilfredsstillende resultater, for eksempel:

• observasjonene er uavhengige;
• det er ingen multikollinearitet blant forklaringsvariablene;
• det er ingen ekstreme uteliggere;
• det er en lineær sammenheng mellom forklaringsvariabler og logiten til responsvariabelen;
• prøvestørrelsen er tilstrekkelig stor.

Legg merke til hvor mange av disse antakelsene som allerede var dekket i vår analyse og behandling av data.

Jeg håper du fortsetter å utforske hva logistisk regresjon har å tilby i alle dens forskjellige tilnærminger!