Matematikere kaster terninger og får stein-papir-saks

Mens Bill Gates forteller historien, utfordret Warren Buffett ham en gang til et terningspill. Hver av dem ville velge en av fire terninger som tilhører Buffett, og deretter kastet de, med det høyeste tallet som vinner. Dette var ikke standardterninger – de hadde et annet utvalg av tall enn de vanlige 1 til 6. Buffett tilbød seg å la Gates velge først, slik at han kunne velge den sterkeste terningen. Men etter at Gates undersøkte terningene, returnerte han et motforslag: Buffett burde velge først.

Gates hadde erkjent at Buffetts terninger viste en merkelig egenskap: Ingen av dem var sterkest. Hvis Gates hadde valgt først, uansett hvilken terning han valgte, ville Buffett ha vært i stand til å finne en annen terning som kunne slå den (det vil si en med mer enn 50 % sjanse til å vinne).

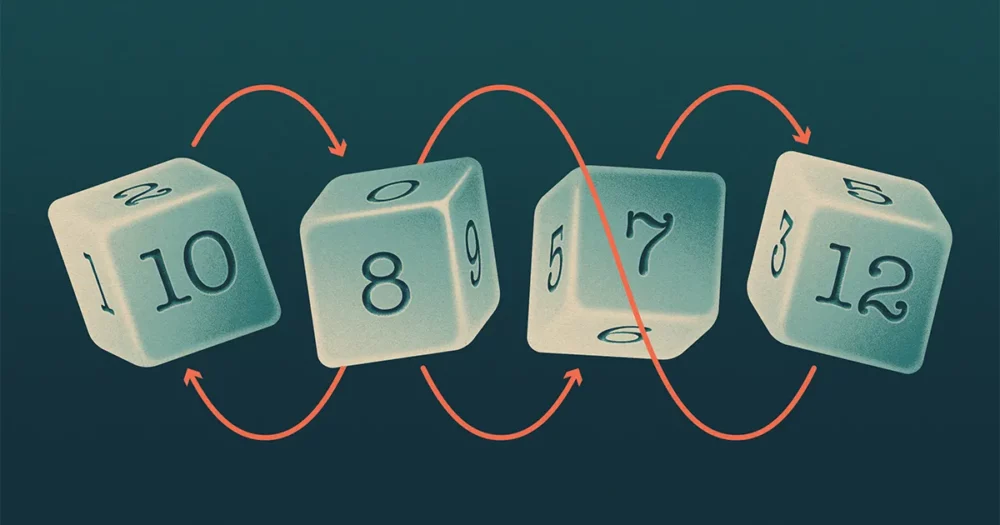
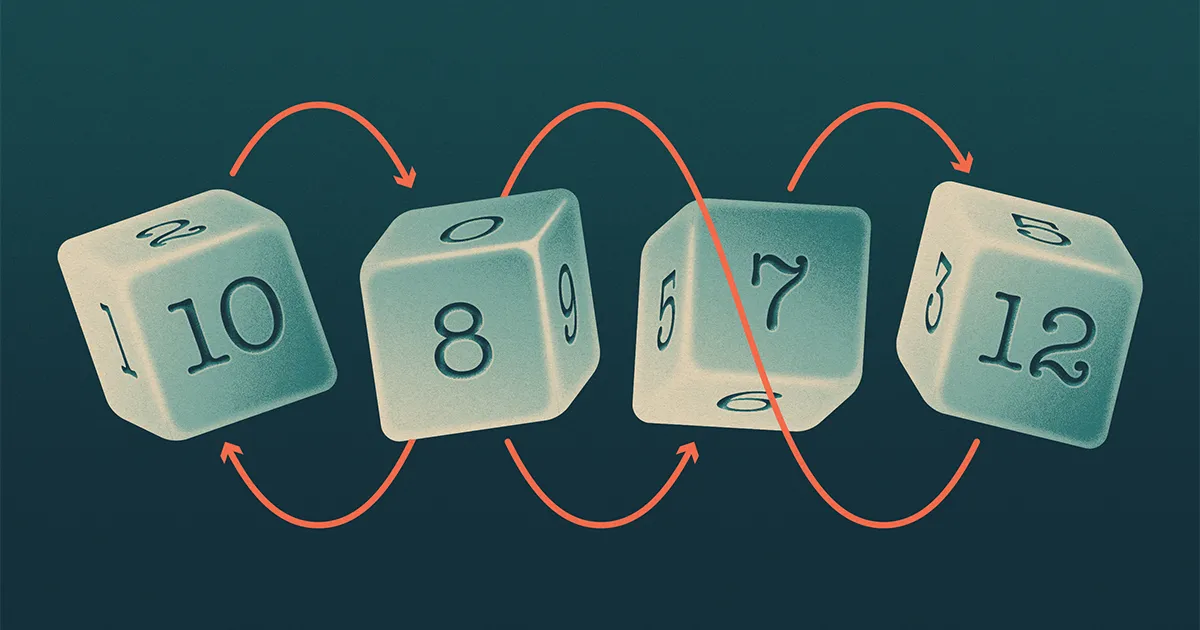
Buffetts fire terninger (kall dem A, B, C og D) dannet et mønster som minner om stein-papir-saks, hvori A beats B, B beats C, C beats D og D beats A. Matematikere sier at et slikt sett med terninger er «intransitive».

"Det er ikke intuitivt i det hele tatt at [intransitive terninger] skal eksistere," sa Brian Conrey, direktøren for American Institute of Mathematics (AIM) i San Jose, som skrev en innflytelsesrik artikkel om emnet i 2013.

Matematikere kom opp med første eksempler av intransitive terninger for mer enn 50 år siden, og til slutt beviste at når du vurderer terninger med flere og flere sider, er det mulig å lage intransitive sykluser av hvilken som helst lengde. Det matematikere ikke visste før nylig, var hvor vanlige intransitive terninger er. Må du konstruere slike eksempler nøye, eller kan du velge terninger tilfeldig og ha en god sjanse til å finne et intransitivt sett?

Ser på tre terninger, hvis du vet det A beats B og B beats C, det virker som bevis på det A er den sterkeste; situasjoner hvor C beats A bør være sjelden. Og faktisk, hvis tallene på terningene tillates å summere seg til forskjellige totaler, så tror matematikere at denne intuisjonen stemmer.

Men a papir lagt ut på nettet sent i fjor viser at i en annen naturlig setting svikter denne intuisjonen spektakulært. Anta at du krever at terningene dine bare bruker tallene som vises på en vanlig terning og har samme sum som en vanlig terning. Da viste avisen, hvis A beats B og B beats C, A og C har i hovedsak like sjanser til å vinne mot hverandre.

"Vet det A beats B og B beats C gir deg bare ingen informasjon om hvorvidt A beats C," sa Timothy Gowers fra University of Cambridge, en Fields-medaljevinner og en av bidragsyterne til det nye resultatet, som ble bevist via et åpent nettbasert samarbeid kjent som et Polymath-prosjekt.

I mellomtiden en annen nyere artikkel analyserer sett med fire eller flere terninger. Det funnet er uten tvil enda mer paradoksalt: Hvis du for eksempel velger fire terninger tilfeldig og du finner ut at A beats B, B beats C og C beats D, så er det litt mer sannsynlig for D å slå A enn omvendt.

Verken sterk eller svak

Det nylige utslettet av resultater startet for omtrent et tiår siden, etter at Conrey deltok på en samling for mattelærere med en økt som dekket intransitive terninger. "Jeg hadde ingen anelse om at slike ting kunne eksistere," sa han. "Jeg ble på en måte fascinert av dem."

Han bestemte seg (senere sammen med sin kollega Kent Morrison på AIM) for å utforske emnet med tre videregående elever han veiledet - James Gabbard, Katie Grant og Andrew Liu. Hvor ofte, lurte gruppen på, vil tilfeldig valgte terninger danne en intransitiv syklus?

Intransitive sett med terninger antas å være sjeldne hvis ansiktstallene til terningene summerer seg til forskjellige totaler, siden terningen med høyest total sannsynligvis vil slå de andre. Så teamet bestemte seg for å fokusere på terninger som har to egenskaper: For det første bruker terningen de samme tallene som på en standard terning – 1 til og med n, i tilfelle av en n-sidig dø. Og for det andre, ansiktstallene summerer seg til samme sum som på en standard terning. Men i motsetning til standardterninger, kan hver terning gjenta noen av tallene og utelate andre.

Når det gjelder sekssidige terninger, er det bare 32 forskjellige terninger som har disse to egenskapene. Så ved hjelp av en datamaskin kunne teamet identifisere alle trippelene der A beats B og B beats C. Forskerne fant, til sin forbauselse, det A beats C i 1,756 trippel og C beats A i 1,731 trippel - nesten identiske tall. Basert på denne beregningen og simuleringer av terninger med mer enn seks sider, laget gjettet at når antall sider på terningen nærmer seg uendelig, er sannsynligheten for at A beats C nærmer seg 50 %.

Formodningen, med sin blanding av tilgjengelighet og nyanser, fant Conrey som god næring for et Polymath-prosjekt, der mange matematikere kommer sammen på nettet for å dele ideer. I midten av 2017 foreslo han ideen til Gowers, opphavsmannen til Polymath-tilnærmingen. "Jeg likte spørsmålet veldig godt på grunn av dets overraskelsesverdi," sa Gowers. Han skrev en blogginnlegg om formodningen som tiltrakk seg en mengde kommentarer, og i løpet av seks ekstra innlegg lyktes kommentatorene i å bevise det.

I deres papir, postet på nettet i slutten av november 2022 innebærer en viktig del av beviset å vise at det for det meste ikke gir mening å snakke om hvorvidt en enkelt terning er sterk eller svak. Buffetts terninger, hvorav ingen er de sterkeste i flokken, er ikke så uvanlige: Hvis du velger en terning tilfeldig, viste Polymath-prosjektet, er det sannsynlig at den slår omtrent halvparten av de andre terningene og taper mot den andre halvparten. "Nesten hver terning er ganske gjennomsnittlig," sa Gowers.

Prosjektet avvek fra AIM-teamets opprinnelige modell på én måte: For å forenkle noen tekniske detaljer, erklærte prosjektet at rekkefølgen på tallene på en terning betyr noe - så for eksempel 122556 og 152562 ville bli betraktet som to forskjellige terninger. Men Polymath-resultatet, kombinert med AIM-teamets eksperimentelle bevis, skaper en sterk antagelse om at formodningen også er sann i den opprinnelige modellen, sa Gowers.

"Jeg var veldig glad for at de kom med dette beviset," sa Conrey.

Når det kom til samlinger av fire eller flere terninger, hadde AIM-teamet spådd lignende oppførsel som tre terninger: For eksempel, hvis A beats B, B beats C og C beats D da bør det være en omtrentlig 50-50 sannsynlighet for at D beats A, nærmer seg nøyaktig 50-50 når antall sider på terningen nærmer seg uendelig.

For å teste antagelsen simulerte forskerne head-to-head-turneringer for sett med fire terninger med 50, 100, 150 og 200 sider. Simuleringene fulgte ikke spådommene deres like nøye som i tilfellet med tre terninger, men var likevel nærme nok til å styrke deres tro på formodningen. Men selv om forskerne ikke var klar over det, bar disse små avvikene et annet budskap: For sett med fire eller flere terninger er formodningen deres falsk.

"Vi ønsket virkelig at [formodningen] skulle være sann, fordi det ville være kult," sa Conrey.

Når det gjelder fire terninger, Elisabetta Cornacchia fra Swiss Federal Institute of Technology Lausanne og Jan Hązła fra African Institute for Mathematical Sciences i Kigali, Rwanda, viste i en papir lagt ut på nettet sent i 2020 at if A beats B, B beats C og C beats D, deretter D har en litt bedre enn 50 % sjanse for å slå A - sannsynligvis et sted rundt 52%, sa Hązła. (Som med Polymath-papiret, brukte Cornacchia og Hązła en litt annen modell enn i AIM-papiret.)

Cornacchia og Hązłas funn kommer av det faktum at selv om en enkelt terning som regel verken vil være sterk eller svak, kan et terningpar noen ganger ha felles styrkeområder. Hvis du velger to terninger tilfeldig, viste Cornacchia og Hązła, er det en anstendig sannsynlighet for at terningene vil være korrelert: De har en tendens til å slå eller tape mot de samme terningene. "Hvis jeg ber deg lage to terninger som er nær hverandre, viser det seg at dette er mulig," sa Hązła. Disse små lommene med korrelasjonsdykk fjerner turneringsresultater fra symmetri så snart det er minst fire terninger i bildet.

De siste avisene er ikke slutten på historien. Cornacchia og Hązłas artikkel begynner bare å avdekke nøyaktig hvordan korrelasjoner mellom terninger ubalanserer symmetrien til turneringer. I mellomtiden vet vi nå at det er mange sett med intransitive terninger der ute – kanskje til og med en som er subtil nok til å lure Bill Gates til å velge først.