Nytt gjennombrudd bringer matrisemultiplikasjon nærmere ideell | Quanta Magazine

Datavitere er en krevende gjeng. For dem er det ikke nok å få det riktige svaret på et problem – målet er nesten alltid å få svaret så effektivt som mulig.

Ta handlingen med å multiplisere matriser, eller matriser med tall. I 1812 kom den franske matematikeren Jacques Philippe Marie Binet opp med det grunnleggende settet med regler vi fortsatt lærer elever. Det fungerer utmerket, men andre matematikere har funnet måter å forenkle og fremskynde prosessen. Nå er oppgaven fremskynde prosessen av matrisemultiplikasjon ligger i skjæringspunktet mellom matematikk og informatikk, hvor forskere fortsetter å forbedre prosessen frem til i dag - selv om gevinstene de siste tiårene har vært ganske beskjedne. Siden 1987 har numeriske forbedringer i matrisemultiplikasjon vært "små og ... ekstremt vanskelige å oppnå," sa François Le Gall, en informatiker ved Nagoya University.

Nå har tre forskere - Ran Duan og Renfei Zhou fra Tsinghua University og Hongxun Wu fra University of California, Berkeley - tatt et stort skritt fremover i å angripe dette flerårige problemet. Deres nye resultater, presentert i november i fjor på Foundations of Computer Science-konferansen, stammer fra en uventet ny teknikk, sa Le Gall. Selv om forbedringen i seg selv var relativt liten, kalte Le Gall den "konseptuelt større enn andre tidligere."

Teknikken avslører en tidligere ukjent og dermed uutnyttet kilde til potensielle forbedringer, og den har allerede båret frukter: Et annet papir, publisert i januar, bygger på den første som viser hvordan matrisemultiplikasjon kan økes ytterligere.

"Dette er et stort teknisk gjennombrudd," sa William Kuszmaul, en teoretisk informatiker ved Harvard University. "Det er den største forbedringen i matrisemultiplikasjon vi har sett på mer enn et tiår."

Gå inn i matrisen

Det kan virke som et uklart problem, men matrisemultiplikasjon er en grunnleggende beregningsoperasjon. Det er integrert i en stor del av algoritmene folk bruker hver dag til en rekke oppgaver, fra å vise skarpere datagrafikk til å løse logistiske problemer i nettverksteori. Og som i andre områder av beregningen, er hastigheten avgjørende. Selv små forbedringer kan til slutt føre til betydelige besparelser av tid, beregningskraft og penger. Men foreløpig er teoretikere hovedsakelig interessert i å finne ut hvor rask prosessen noen gang kan være.

Den tradisjonelle måten å multiplisere to på n-av-n matriser - ved å multiplisere tall fra hver rad i den første matrisen med tall i kolonnene i den andre - krever n³ separate multiplikasjoner. For 2-av-2-matriser betyr det 2³ eller 8 multiplikasjoner.

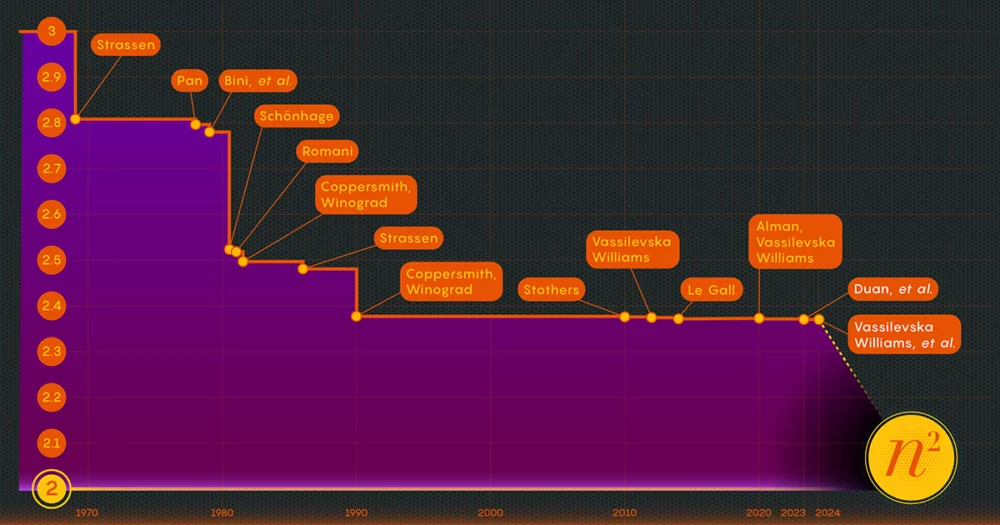
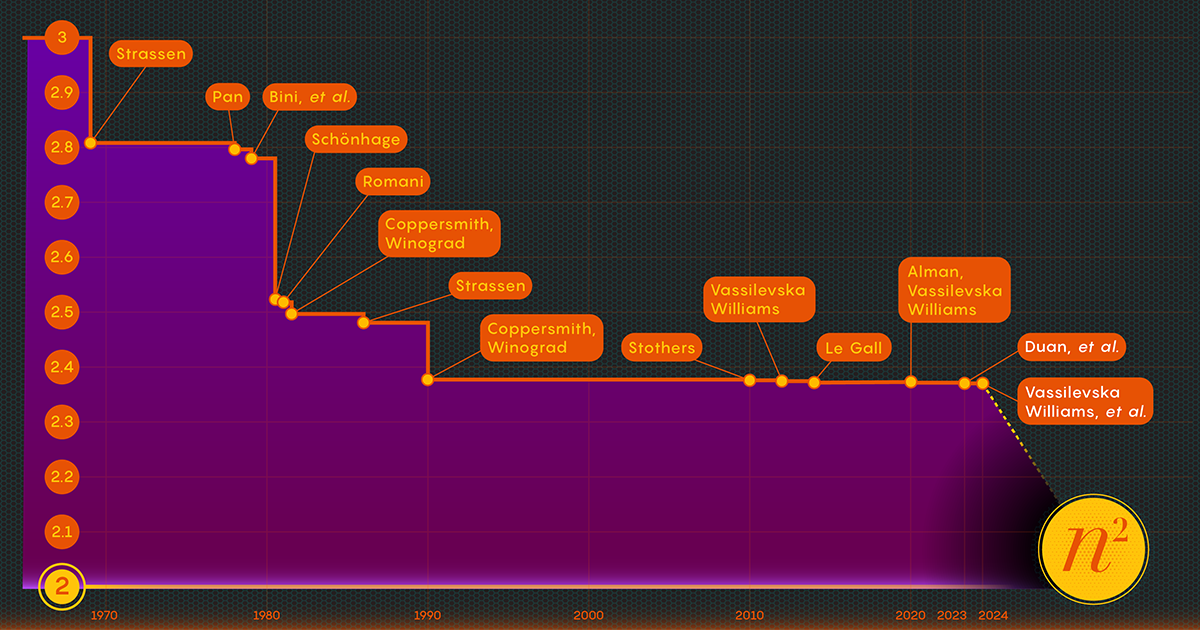
I 1969 avslørte matematikeren Volker Strassen en mer komplisert prosedyre som kunne multiplisere 2 x 2 matriser i bare syv multiplikasjonstrinn og 18 addisjoner. To år senere demonstrerte informatikeren Shmuel Winograd at syv faktisk er det absolutte minimum for 2 x 2 matriser.

Strassen utnyttet den samme ideen for å vise at alle større n-av-n matriser kan også multipliseres med færre enn n³ trinn. Et nøkkelelement i denne strategien involverer en prosedyre som kalles dekomponering - å bryte ned en stor matrise i suksessivt mindre submatriser, som kan ende opp med å bli så små som 2 x 2 eller til og med 1 x 1 (dette er bare enkelttall).

Begrunnelsen for å dele et gigantisk utvalg i bittesmå biter er ganske enkelt, ifølge Virginia Vassilevska Williams, en informatiker ved Massachusetts Institute of Technology og medforfatter av en av de nye papirene. "Det er vanskelig for et menneske å se på en stor matrise (si størrelsesorden 100 x 100) og tenke på den best mulige algoritmen," sa Vassilevska Williams. Selv 3-av-3-matriser er ikke fullstendig løst ennå. "Likevel kan man bruke en rask algoritme som man allerede har utviklet for små matriser for også å få en rask algoritme for større matriser."

Nøkkelen til hastighet, har forskere fastslått, er å redusere antall multiplikasjonstrinn, og senke eksponenten fra n³ (for standardmetoden) så mye de kan. lavest mulig verdi, n², er i utgangspunktet så lang tid det tar bare å skrive svaret. Dataforskere omtaler den eksponenten som omega, ω, med n^ω være færrest mulig trinn som trengs for å lykkes med å multiplisere to n-av-n matriser som n vokser seg veldig stor. "Poenget med dette arbeidet," sa Zhou, som også var medforfatter av papiret fra januar 2024, "er å se hvor nær to du kan komme, og om det kan oppnås i teorien."

Et laserfokus

I 1986 fikk Strassen nok et stort gjennombrudd da han introdusert det som kalles lasermetoden for matrisemultiplikasjon. Strassen brukte det til å etablere en øvre verdi for omega på 2.48. Mens metoden bare er ett trinn i store matrisemultiplikasjoner, er den en av de viktigste fordi forskere har fortsatt å forbedre den.

Ett år senere introduserte Winograd og Don Coppersmith en ny algoritme som perfekt komplementerte lasermetoden. Denne kombinasjonen av verktøy har vært med i praktisk talt alle påfølgende forsøk på å øke hastigheten på matrisemultiplikasjon.

Her er en forenklet måte å tenke på hvordan disse ulike elementene passer sammen. La oss starte med to store matriser, A og B, som du vil multiplisere sammen. Først dekomponerer du dem i mange mindre submatriser, eller blokker, som de noen ganger kalles. Deretter kan du bruke Coppersmith og Winograds algoritme til å tjene som en slags bruksanvisning for håndtering og til slutt montering av blokkene. "Den forteller meg hva jeg skal multiplisere og hva jeg skal legge til og hvilke oppføringer som går hvor" i produktmatrisen C, sa Vassilevska Williams. "Det er bare en oppskrift for å bygge opp C fra A og B."

Det er imidlertid en hake: Noen ganger ender du opp med blokker som har oppføringer til felles. Å la disse ligge i produktet vil være det samme som å telle disse oppføringene to ganger, så på et tidspunkt må du kvitte deg med de dupliserte termene, kalt overlappinger. Forskere gjør dette ved å "drepe" blokkene de er i - sette komponentene lik null for å fjerne dem fra beregningen.

Det er der Strassens lasermetode endelig kommer inn i bildet. "Lasermetoden fungerer vanligvis veldig bra og finner generelt en god måte å drepe en undergruppe av blokker for å fjerne overlappingen," sa Le Gall. Etter at laseren har eliminert, eller "brent bort", alle overlappingene, kan du konstruere den endelige produktmatrisen, C.

Å sette disse forskjellige teknikkene sammen resulterer i en algoritme for å multiplisere to matriser med et bevisst gjerrig antall multiplikasjoner totalt sett - i det minste i teorien. Lasermetoden er ikke ment å være praktisk; det er bare en måte å tenke på den ideelle måten å multiplisere matriser på. "Vi kjører aldri metoden [på en datamaskin]," sa Zhou. "Vi analyserer det."

Og den analysen er det som førte til den største forbedringen av omega på mer enn et tiår.

Et tap er funnet

Fjor sommers papir, av Duan, Zhou og Wu, viste at Strassens prosess fortsatt kunne fremskyndes betydelig. Alt var på grunn av et konsept de kalte et skjult tap, begravd dypt i tidligere analyser - "et resultat av utilsiktet dreping av for mange blokker," sa Zhou.

Lasermetoden fungerer ved å merke blokker med overlapp som søppel, beregnet for avhending; andre blokker anses som verdige og vil bli reddet. Utvelgelsesprosessen er imidlertid noe randomisert. En blokk vurdert som søppel kan faktisk vise seg å være nyttig tross alt. Dette var ikke en total overraskelse, men ved å undersøke mange av disse tilfeldige valgene, bestemte Duans team at lasermetoden systematisk undervurderte blokker: Flere blokker skulle reddes og færre kastes ut. Og, som vanligvis er tilfellet, gir mindre avfall større effektivitet.

"Å kunne beholde flere blokker uten overlapping fører dermed til ... en raskere matrisemultiplikasjonsalgoritme," sa Le Gall.

Etter å ha bevist eksistensen av dette tapet, endret Duans team måten lasermetoden merket blokker på, og reduserte avfallet betydelig. Som et resultat satte de en ny øvre grense for omega på rundt 2.371866 - en forbedring i forhold til den forrige øvre grensen på 2.3728596, satt i 2020 av Josh Alman og Vassilevska Williams. Det kan virke som en beskjeden endring, som senker grensen med omtrent 0.001. Men det er den største enkeltforbedringen forskerne har sett siden 2010. Vassilevska Williams og Almans 2020-resultat ble til sammenligning bare forbedret med 0.00001 i forhold til forgjengeren.

Men det som er mest spennende for forskere er ikke bare selve den nye rekorden – som ikke varte lenge. Det er også det faktum at avisen avslørte en ny vei for forbedring som inntil da hadde gått helt ubemerket hen. I nesten fire tiår har alle vært avhengige av den samme lasermetoden, sa Le Gall. "Så fant de ut at vi kan gjøre det bedre."

Papiret fra januar 2024 foredlet denne nye tilnærmingen, og gjorde det mulig for Vassilevska Williams, Zhou og deres medforfattere å redusere det skjulte tapet ytterligere. Dette førte til en ytterligere forbedring av omegas øvre grense, og reduserte den til 2.371552. Forfatterne generaliserte også den samme teknikken for å forbedre multiplikasjonsprosessen for rektangulære (n-av-m) matriser — en prosedyre som har applikasjoner innen grafteori, maskinlæring og andre områder.

Noen ytterligere fremskritt langs disse linjene er nesten sikkert, men det er grenser. I 2015, Le Gall og to samarbeidspartnere beviste at dagens tilnærming - lasermetoden kombinert med Coppersmith-Winograd-oppskriften - ikke kan gi en omega under 2.3078. For å gjøre ytterligere forbedringer, sa Le Gall, "du må forbedre den opprinnelige [tilnærmingen] til Coppersmith og Winograd som egentlig ikke har endret seg siden 1987». Men så langt har ingen kommet opp med en bedre måte. Det er kanskje ikke engang en.

"Å forbedre omega er faktisk en del av å forstå dette problemet," sa Zhou. "Hvis vi kan forstå problemet godt, kan vi designe bedre algoritmer for det. [Og] folk er fortsatt i de tidlige stadiene av å forstå dette eldgamle problemet."