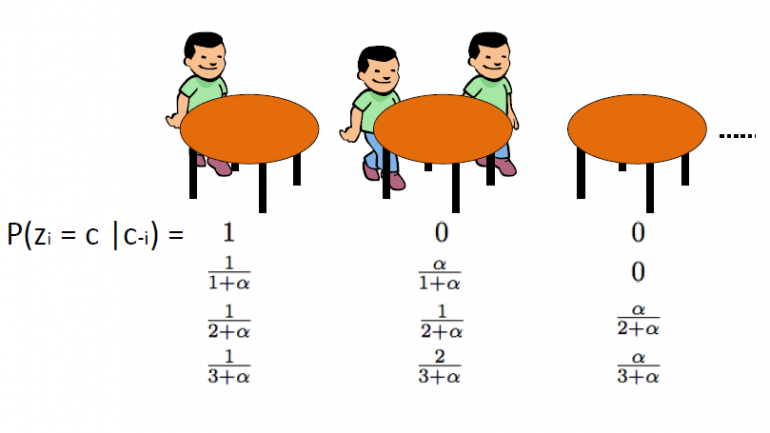Dirichlet behandler den kinesiske restaurantprosessen og andre representasjoner

• Kan 20, 2014
• Vasilis Vryniotis
• . Ingen kommentarer

Denne artikkelen er den tredje delen av serien Clustering with Dirichlet Process Mixture Models. Forrige gang vi definerte Finite Mixture Model basert på Dirichlet Distribution, og vi stilte spørsmål om hvordan vi kan gjøre denne modellen uendelig. Vi diskuterte kort ideen om å ta grensen for modellen når k antall klynger har en tendens til uendelig, men som vi understreket eksistensen av et slikt objekt er ikke trivielt ”?). Som en påminnelse er grunnen til at vi ønsker å gjøre k uendelig fordi vi på denne måten vil ha en ikke-parametrisk modell som ikke krever at vi forhåndsdefinerer det totale antall klynger i dataene.

Oppdatering: Datumbox Machine Learning Framework er nå åpen kildekode og gratis å nedlasting. Sjekk ut pakken com.datumbox.framework.machinelearning.clustering for å se implementeringen av Dirichlet Process Mixture Models i Java.

Selv om målet vårt er å bygge en modell som er i stand til å utføre klynging på datasett, må vi diskutere om Dirichlet-prosesser før det. Vi vil gi både de strenge matematiske definisjonene og de mer intuitive forklaringene på DP, og vi vil diskutere måter å konstruere prosessen på. Disse konstruksjonene / representasjonene kan sees på som en måte å finne forekomster av Dirichlet-prosessen i "det virkelige liv".

Til tross for at jeg prøvde å tilpasse forskningsrapporten min på en slik måte at disse blogginnleggene er lettere å følge, er det fortsatt viktig å definere nødvendige matematiske verktøy og distribusjoner før vi hopper inn i å bruke modellene. Dirichlet Process-modeller er et tema for aktiv forskning, men de krever god forståelse av statistikk og stokastiske prosesser før du bruker dem. Et annet problem er at som vi vil se i denne artikkelen, kan Dirichlet-prosesser representeres / konstrueres på mange måter. Som et resultat bruker flere fagoppgaver helt forskjellige notasjoner / konvensjoner og undersøker problemet fra forskjellige synsvinkler. I dette innlegget prøver jeg å forklare dem så enkle som mulig og bruke samme notasjon. Forhåpentligvis vil ting bli tydeligere med de to kommende artiklene som fokuserer på definisjonen av Dirichlet Process Mixture Modeller og på hvordan du faktisk kan bruke dem til å utføre klyngeanalyse.

1. Definisjon av Dirichlet-prosessen

En Dirichlet-prosess over et Θ rom er en stokastisk prosess. Det er en sannsynlighetsfordeling over "sannsynlighetsfordeling over Θ rom" og a tegne fra det er en diskret fordeling. Mer formelt er en Dirichlet Distribution en fordeling over sannsynlighetstiltak. EN sannsynlighetstiltak er en funksjon av delmengder av mellomrom Θ til [0,1]. G er et DP-distribuert tilfeldig sannsynlighetsmål, betegnet som , hvis det er noen partisjon (A₁,…EN_n) av rom Θ vi har det .

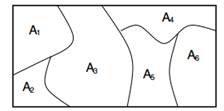
Figur 1: Margener på uendelige partisjoner er Dirichlet distribuert.

DP har to parametere: Den første er basefordelingen G₀ som fungerer som et middel . Den andre er styrkeparameteren α som er strengt positiv og fungerer som omvendt varians . Den bestemmer omfanget av repetisjonen av verdiene til utgangsfordelingen. Jo høyere verdien av a, jo mindre blir repetisjonen; jo mindre verdien er, desto høyere blir repetisjonen av verdiene for utgangsfordeling. Til slutt er Θ-rommet parameterområdet som vi definerer DP på. Dessuten er rommet Θ også definisjonen til G₀ som er den samme som den av G.

En enklere og mer intuitiv måte å forklare en Dirichlet-prosess er følgende. Anta at vi har et mellomrom Θ som kan deles på en hvilken som helst begrenset måte (A₁,…,EN_n) og en sannsynlighetsfordeling G som tilordner sannsynligheter til dem. G er en spesifikk sannsynlighetsfordeling over Θ, men det er mange andre. Dirichlet-prosessen på Θ modellerer akkurat dette; det er en fordeling over alle mulige sannsynlighetsfordelinger på plass Θ. Dirichlet-prosessen er parameterisert med G₀ basisfunksjon og α konsentrasjonsparameter. Vi kan si at G er fordelt i henhold til DP med parametrene α og G₀ hvis den felles fordelingen av sannsynlighetene som G tilordner partisjonene til Θ følger Dirichlet-fordelingen. Alternativt kan vi si at sannsynlighetene som G tilordner til en endelig partisjon av Θ følger Dirichlet Distribution.

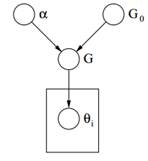
Figur 2: Grafisk modell av Dirichlet-prosessen

Endelig over kan vi se grafisk modell av en DP. Vi bør merke oss at α er et skalar hyperparameter, G₀ er grunnfordelingen til DP, G en tilfeldig fordeling over Θ parameterrom samplet fra DP som tilordner sannsynligheter til parametrene og θ_i er en parametervektor som er trukket fra G-fordelingen og det er et element i Θ-rommet.

2. Posterior Dirichlet-prosesser

Posterior Dirichlet Processes ble diskutert av Ferguson. Vi starter med å tegne et tilfeldig sannsynlighetsmål G fra en Dirichlet-prosess, . Siden G er en sannsynlighetsfordeling over Θ, kan vi også prøve fra denne fordelingen og tegne uavhengige identisk fordelte prøver samples₁,…, Θ_n ~ G. Siden trekk fra en Dirichlet-prosess er diskrete distribusjoner, kan vi representere hvor er en kort notasjon for som er en delta-funksjon som tar 1 hvis og 0 andre steder. En interessant effekt av dette er at siden G er definert på denne måten, er det en positiv sannsynlighet for at forskjellige prøver har samme verdi . Som vi vil se senere, skaper dette en klyngeeffekt som kan brukes til å utføre klyngeanalyse på datasett.

Ved å bruke definisjonene og observasjonene ovenfor ønsker vi å estimere den bakre delen av Dirichlet-prosessen gitt prøvene θ. Likevel siden vi vet det og ved å bruke Bayes-reglene og konjugasjonen mellom Dirichlet og Multinomial har vi det og .

Likning 1: Posterior Dirichlet Process

Denne egenskapen er veldig viktig, og den brukes av de forskjellige DP-representasjonene.

3. Dirichlet-prosessrepresentasjoner

I de foregående segmentene definerte vi Dirichlet-prosessen og presenterte den teoretiske modellen. Et viktig spørsmål vi må svare på er hvordan vi vet at et slikt objekt eksisterer og hvordan vi kan konstruere og representere en Dirichlet-prosess.

De første indikasjonene på eksistens ble gitt av Ferguson som brukte Kolmogorov-konsistenssetningen, ga definisjonen av en Dirichlet-prosess og beskrev den Posterior Dirichlet-prosessen. Fortsetter sin forskning, Blackwell og MacQueen brukte de Finettis teorem for å bevise eksistensen av et slikt tilfeldig sannsynlighetstiltak og introduserte Blackwell-MacQueen urneskjemaet som tilfredsstiller egenskapene til Dirichlet Process. I 1994 Sethuraman ga en ekstra enkel og direkte måte å konstruere en DP ved å introdusere den Stick-breaking konstruksjonen. Endelig ble en annen representasjon levert av Aldous som introduserte den kinesiske restaurantprosessen som en effektiv måte å konstruere en Dirichlet-prosess på.

De forskjellige representasjonene av Dirichlet-prosessen er matematisk likeverdige, men formuleringen deres er forskjellig fordi de undersøker problemet fra forskjellige synsvinkler. Nedenfor presenterer vi de vanligste representasjonene som finnes i litteraturen, og vi fokuserer på den kinesiske restaurantprosessen som gir en enkel og beregningseffektiv måte å konstruere inferensealgoritmer for Dirichlet Process.

3.1 Blackwell-MacQueen-urneordningen

Blackwell-MacQueen urneskjemaet kan brukes til å representere en Dirichlet-prosess, og den ble introdusert av Blackwell og MacQueen. Den er basert på Pólya-urneskjemaet som kan sees på som den motsatte modellen for prøvetaking uten erstatning. I Pólya-urneskjemaet antar vi at vi har en ikke-gjennomsiktig urn som inneholder fargede kuler, og vi tegner kuler tilfeldig. Når vi tegner en ball, observerer vi fargen på den, vi legger den tilbake i urnen og legger til en ekstra ball i samme farge. En lignende ordning brukes av Blackwell og MacQueen for å konstruere en Dirichlet-prosess.

Dette skjemaet produserer en sekvens av θ₁,θ₂, ... med betingede sannsynligheter . I denne ordningen antar vi at G₀ er en fordeling over farger og hver θ_n representerer fargen på ballen som er plassert i urnen. De algoritme er som følger:

· Vi starter med en tom urne.

· Med sannsynlighet proporsjonal med α vi tegner og vi legger til en ball av denne fargen i urnen.

· Med sannsynlighet proporsjonal med n-1 trekker vi en tilfeldig ball fra urnen, vi observerer fargen, vi plasserer den tilbake til urnen, og vi legger til en ekstra ball av samme farge i urnen.

Tidligere startet vi med en Dirichlet-prosess og avledet Blackwell-MacQueen-ordningen. La oss nå starte omvendt fra Blackwell-MacQueen-ordningen og utlede DP. Siden θ_i ble trukket på en mild måte fra G, vil deres felles fordeling være uforanderlig i forhold til endelige permutasjoner, og dermed kan de byttes ut. Ved å bruke de Finettis teorem har vi derfor at det må eksistere en fordeling over tiltak for å gjøre dem iide, og denne fordelingen er Dirichlet-prosessen. Som et resultat viser vi at Blackwell-MacQueen-urneskjemaet er en representasjon av DP, og det gir oss en konkret måte å konstruere den på. Som vi vil se senere, tilsvarer denne ordningen matematisk den kinesiske restaurantprosessen.

3.2 Den stikkbrytende konstruksjonen

Stick-breaking konstruksjonen er en alternativ måte å representere en Dirichlet-prosess som ble introdusert av Sethuraman. Det er en konstruktiv måte å danne distribusjon og bruker følgende analogi: Vi antar at vi har en pinne med lengde 1, vi bryter den i posisjon β₁ og vi tildeler π₁ lik lengden på den delen av pinnen vi brøt. Vi gjentar den samme prosessen for å oppnå π₂, Pi₃,… etc; på grunn av måten denne ordningen er definert på, kan vi fortsette å gjøre det uendelige tider.

Basert på ovenstående π_k kan modelleres som , Hvor mens som i de forrige skjemaene θ samples direkte av Base-distribusjonen . Følgelig kan G-fordelingen skrives som en sum av delta-funksjoner vektet med π_k sannsynligheter som er lik . Dermed gir den stikkbrytende konstruksjonen oss en enkel og intuitiv måte å konstruere en Dirichlet-prosess på.

3.3 Den kinesiske restaurantprosessen

The Chinese Restaurant Process, som ble introdusert av Aldous, er en annen effektiv måte å representere en Dirichlet-prosess på, og den kan knyttes direkte til Blackwell-MacQueen-urneopplegget. Denne ordningen bruker følgende analogi: Vi antar at det er en kinesisk restaurant med uendelig mange bord. Når kundene kommer inn i restauranten, sitter de tilfeldig til et av de okkuperte bordene, eller de velger å sitte ved det første tilgjengelige tomme bordet.

CRP definerer en fordeling på rommet for partisjoner av de positive heltallene. Vi starter med å tegne θ₁,… Θ_n fra Blackwell-MacQueen-urneopplegget. Som vi diskuterte i de foregående segmentene, forventer vi å se en grupperingseffekt, og dermed vil det totale antallet unike θ-verdier k være betydelig mindre enn n. Dermed definerer dette en partisjon av settet {1,2,…, n} i k-klynger. Følgelig induserer tegning fra Blackwell-MacQueen urneskjemaet en tilfeldig partisjon av settet {1,2,…, n}. Den kinesiske restaurantprosessen er dette indusert distribusjon over partisjoner. Algoritmen er som følger:

· Vi starter med en tom restaurant.

· den 1^st kunden sitter alltid på 1^st bord

· N + 1^th kunden har to alternativer:

o Sett deg på det første ledige bordet med sannsynlighet

o Sett deg på et av de kth okkuperte bordene med sannsynlighet
hvor er antall mennesker som sitter på bordet

Hvor α er spredningsverdien til DP og n er det totale antallet kunder i restauranten på et gitt tidspunkt. Den latente variabelen z_i lagrer tabellnummeret til i^th kunde og tar verdier fra 1 til k_n hvor k_n er det totale antall okkuperte bord når n kunder er i restauranten. Vi bør merke oss at k_n vil alltid være mindre eller lik n og i gjennomsnitt handler det om . Til slutt skal vi merke oss at sannsynligheten for bordoppsett er uforanderlig til permutasjoner. Dermed er z_i kan byttes ut, noe som betyr at bord med samme størrelse på kunder har samme sannsynlighet.

Den kinesiske restaurantprosessen er sterkt knyttet til Pólya-urnearrangementet og Dirichlet-prosessen. CRP er en måte å spesifisere en distribusjon over partisjoner (tabelloppgaver) på n poeng og kan brukes som en prior på rommet for latent variabel z_i hvilken bestemmer klyngetildelingene. CRP tilsvarer Pólyas urneskjema med bare forskjellen at den ikke tildeler parametere til hver tabell / klynge. Å gå fra CRP til Pólyas urneskjema vi tegner for alle tabeller k = 1,2… og deretter for hver x_i som er gruppert til tabell z_i tilordne en . Med andre ord tilordne den nye x_i parameteren θ i tabellen. Endelig siden vi kan ikke tildele θ til uendelige tabeller fra begynnelsen, kan vi bare tildele en ny θ hver gang noen sitter på et nytt bord. På grunn av alt det ovennevnte kan CRP hjelpe oss med å bygge beregningseffektive algoritmer for å utføre klyngeanalyse på datasett.

I dette innlegget diskuterte vi Dirichlet-prosessen og flere måter å konstruere den på. Vi vil bruke ideene ovenfor i neste artikkel. Vi vil introdusere Dirichlet Process Mixture Model og vi vil bruke den kinesiske restaurantrepresentasjonen for å konstruere Dirichlet Process og preform Cluster Analysis. Hvis du savnet noen få poeng, ikke bekymre deg, da ting vil begynne å bli tydeligere med de neste to artiklene.

Jeg håper du syntes dette innlegget var interessant. Hvis du gjorde det, ta deg tid til å dele det på Facebook og Twitter. 🙂