Notacja Big O i analiza algorytmów na przykładach w Pythonie

Wprowadzenie

Zwykle istnieje wiele sposobów rozwiązania problemu za pomocą programu komputerowego. Na przykład istnieje kilka sposobów sortowania elementów w tablicy – ​​możesz użyć scalanie sortuj, sortowanie bąbelkowe, sortowanie przez wstawianie, i tak dalej. Wszystkie te algorytmy mają swoje zalety i wady, a zadaniem programisty jest ich ważenie, aby móc wybrać najlepszy algorytm do użycia w dowolnym przypadku użycia. Innymi słowy, głównym pytaniem jest, którego algorytmu użyć do rozwiązania konkretnego problemu, gdy istnieje wiele rozwiązań problemu.

Analiza algorytmu odnosi się do analizy złożoności różnych algorytmów i znalezienia najbardziej wydajnego algorytmu do rozwiązania danego problemu. Notacja Big-O to miara statystyczna używana do opisu złożoności algorytmu.

W tym przewodniku najpierw dokonamy krótkiego przeglądu analizy algorytmów, a następnie przyjrzymy się dokładniej notacji Big-O. Zobaczymy, jak można wykorzystać notację Big-O do znalezienia złożoności algorytmu za pomocą różnych funkcji Pythona.

Dlaczego analiza algorytmu jest ważna?

Aby zrozumieć, dlaczego analiza algorytmów jest ważna, posłużymy się prostym przykładem. Załóżmy, że kierownik daje dwóm swoim pracownikom zadanie zaprojektowania algorytmu w Pythonie, który oblicza silnię liczby wprowadzonej przez użytkownika. Algorytm opracowany przez pierwszego pracownika wygląda tak:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Zauważ, że algorytm po prostu przyjmuje liczbę całkowitą jako argument. W środku fact() funkcja zmienna o nazwie product jest inicjowany do 1. Pętla jest wykonywana z 1 do n a podczas każdej iteracji wartość w product jest mnożony przez liczbę iterowaną przez pętlę, a wynik jest zapisywany w product ponownie zmienna. Po wykonaniu pętli, product zmienna będzie zawierać silnię.

Podobnie, drugi pracownik również opracował algorytm, który oblicza silnię liczby. Drugi pracownik wykorzystał funkcję rekurencyjną do obliczenia silni liczby n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Menedżer musi zdecydować, którego algorytmu użyć. W tym celu postanowili wybrać, który algorytm działa szybciej. Jednym ze sposobów na to jest znalezienie czasu potrzebnego do wykonania kodu na tym samym wejściu.

W notatniku Jupyter możesz użyć %timeit literał, po którym następuje wywołanie funkcji, aby znaleźć czas potrzebny do wykonania funkcji:

%timeit fact(50)

To da nam:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Wynik mówi, że algorytm trwa 9 mikrosekund (plus/minus 45 nanosekund) na pętlę.

Podobnie możemy obliczyć, ile czasu zajmuje wykonanie drugiego podejścia:

%timeit fact2(50)

Spowoduje to:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Drugi algorytm z rekurencją trwa 15 mikrosekund (plus/minus 427 nanosekund).

Czas wykonania pokazuje, że pierwszy algorytm jest szybszy w porównaniu z drugim algorytmem z rekurencją. Kiedy mamy do czynienia z dużymi danymi wejściowymi, różnica w wydajności może stać się bardziej znacząca.

Jednak czas wykonania nie jest dobrym miernikiem do pomiaru złożoności algorytmu, ponieważ zależy on od sprzętu. Potrzebna jest bardziej obiektywna metryka analizy złożoności dla algorytmu. To tutaj notacja duże O przychodzi grać.

Analiza algorytmu z notacją Big-O

Notacja Big-O oznacza związek między danymi wejściowymi algorytmu a krokami wymaganymi do wykonania algorytmu. Jest oznaczony przez duże „O”, po którym następuje otwierający i zamykający nawias. Wewnątrz nawiasu związek między danymi wejściowymi a krokami podejmowanymi przez algorytm jest przedstawiony za pomocą „n”.

Kluczowym wnioskiem jest – Big-O nie jest zainteresowany a szczególny przypadek, w którym uruchamiasz algorytm, taki jak fact(50), ale raczej jak dobrze to robi skala biorąc pod uwagę rosnący wkład. Jest to znacznie lepsza metryka do oceny niż konkretny czas dla konkretnej instancji!

Na przykład, jeśli istnieje zależność liniowa między wejściem a krokiem podjętym przez algorytm w celu zakończenia jego wykonania, zastosowana notacja Big-O będzie Na). Podobnie notacja Big-O dla funkcje kwadratowe is O(n²).

Aby zbudować intuicję:

• Na): w n=1, zostaje wykonany 1 krok. Na n=10, wykonuje się 10 kroków.
• O(n²): w n=1, zostaje wykonany 1 krok. Na n=10, wykonuje się 100 kroków.

At n=1, te dwa wykonałyby to samo! Jest to kolejny powód, dla którego obserwowanie związku między danymi wejściowymi a liczbą kroków do przetworzenia danych wejściowych jest lepsze niż samo ocenianie funkcji z konkretnymi danymi wejściowymi.

Oto niektóre z najczęstszych funkcji Big-O:

Imię	Big O
stały	O (c)
Liniowy	Na)
Kwadratowy	O(n²)
Sześcienny	O(n³)
Wykładniczy	O(2ⁿ)
Logarytmiczna	O (log (n))
Dziennik liniowy	O(nlog(n))

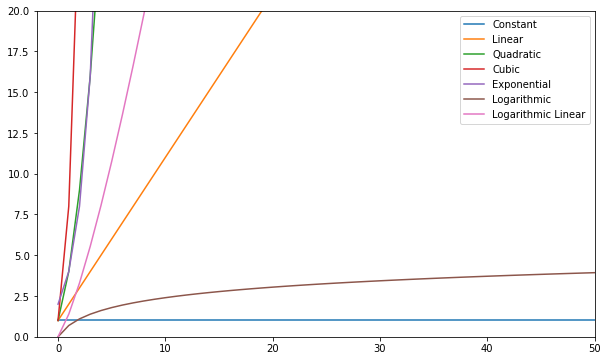
Możesz zwizualizować te funkcje i porównać je:

Ogólnie rzecz biorąc – wszystko, co gorsze niż liniowe jest uważane za złą złożoność (tj. nieefektywne) i powinno się tego unikać, jeśli to możliwe. Złożoność liniowa jest w porządku i zwykle jest złem koniecznym. Logarytmiczna jest dobra. Stała jest niesamowita!

Aby zorientować się, jak obliczane jest Big-O, spójrzmy na kilka przykładów stałej, liniowej i kwadratowej złożoności.

Stała złożoność – O(C)

Mówi się, że złożoność algorytmu jest stała, jeśli kroki wymagane do zakończenia wykonania algorytmu pozostają stałe, niezależnie od liczby danych wejściowych. Stała złożoność jest oznaczona przez O (c) gdzie c może być dowolną stałą liczbą.

Napiszmy prosty algorytm w Pythonie, który odnajdzie kwadrat pierwszej pozycji na liście, a następnie wypisze go na ekranie:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

W powyższym skrypcie niezależnie od wielkości wejściowejlub liczba pozycji na liście wejściowej itemsalgorytm wykonuje tylko 2 kroki:

1. Znalezienie kwadratu pierwszego elementu
2. Drukowanie wyniku na ekranie.

Stąd złożoność pozostaje stała.

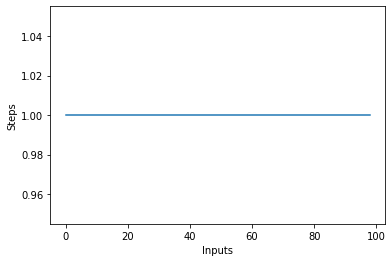
Jeśli narysujesz wykres liniowy o różnej wielkości items dane wejściowe na osi X i liczbę kroków na osi Y, otrzymasz linię prostą. Stwórzmy krótki skrypt, który pomoże nam to zwizualizować. Bez względu na liczbę wejść, liczba wykonanych kroków pozostaje taka sama:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Złożoność liniowa – Na)

Mówi się, że złożoność algorytmu jest liniowa, jeśli kroki wymagane do wykonania algorytmu rosną lub maleją liniowo wraz z liczbą wejść. Złożoność liniowa jest oznaczona przez Na).

W tym przykładzie napiszmy prosty program, który wyświetla w konsoli wszystkie pozycje z listy:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Złożoność linear_algo() funkcja jest liniowa w powyższym przykładzie, ponieważ liczba iteracji pętli for będzie równy rozmiarowi wejścia items szyk. Na przykład, jeśli w items listy, pętla for zostanie wykonana 4 razy.

Stwórzmy szybko wykres dla algorytmu złożoności liniowej z liczbą wejść na osi x i liczbą kroków na osi y:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Spowoduje to:

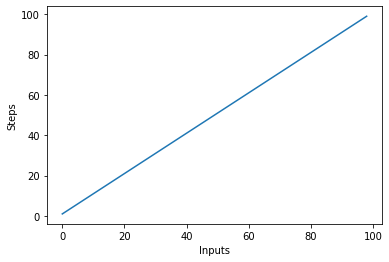
Ważną rzeczą do zapamiętania jest to, że przy dużych nakładach, stałe mają tendencję do utraty wartości. Dlatego zazwyczaj usuwamy stałe z notacji Big-O, a wyrażenie takie jak O(2n) jest zwykle skracane do O(n). Zarówno O(2n), jak i O(n) są liniowe – liczy się zależność liniowa, a nie konkretna wartość. Na przykład zmodyfikujmy linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Istnieją dwie pętle for, które iterują po wejściu items lista. Dlatego złożoność algorytmu staje się O (2n), jednak w przypadku nieskończonych elementów na liście wejściowej podwójna nieskończoność jest nadal równa nieskończoności. Możemy zignorować stałą 2 (ponieważ jest to ostatecznie nieistotne), a złożoność algorytmu pozostaje Na).

Zwizualizujmy ten nowy algorytm, wykreślając dane wejściowe na osi X i liczbę kroków na osi Y:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

W powyższym skrypcie widać to wyraźnie y=2njednak wynik jest liniowy i wygląda tak:

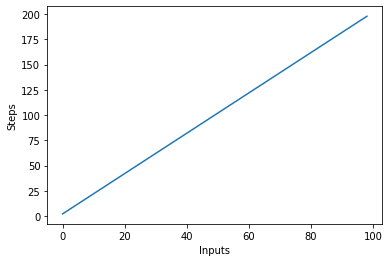
Złożoność kwadratowa – O(n²)

Mówi się, że złożoność algorytmu jest kwadratowa, gdy kroki wymagane do wykonania algorytmu są kwadratową funkcją liczby elementów na wejściu. Złożoność kwadratową oznaczono jako O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Mamy zewnętrzną pętlę, która iteruje przez wszystkie elementy na liście wejściowej, a następnie zagnieżdżoną pętlę wewnętrzną, która ponownie przechodzi przez wszystkie elementy na liście wejściowej. Całkowita liczba wykonanych kroków wynosi n*n, gdzie n to liczba elementów w tablicy wejściowej.

Poniższy wykres przedstawia liczbę wejść w zależności od kroków algorytmu o kwadratowej złożoności:

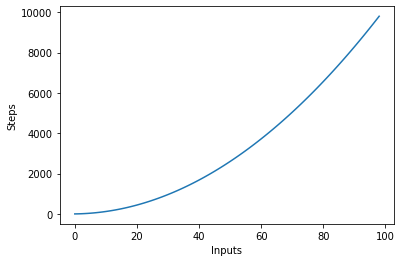
Złożoność logarytmiczna – O (logn)

Niektóre algorytmy osiągają złożoność logarytmiczną, na przykład Wyszukiwanie binarne. Wyszukiwanie binarne wyszukuje element w tablicy, sprawdzając środkowy tablicy i przycinanie połowy, w której element nie jest. Robi to ponownie przez pozostałą połowę i kontynuuje te same kroki, aż element zostanie znaleziony. Na każdym kroku to połówki liczba elementów w tablicy.

Wymaga to posortowania tablicy, a my możemy przyjąć założenie dotyczące danych (takich jak sortowanie).

Kiedy możesz przyjąć założenia dotyczące przychodzących danych, możesz podjąć kroki, które zmniejszają złożoność algorytmu. Złożoność logarytmiczna jest pożądana, ponieważ osiąga dobrą wydajność nawet przy bardzo skalowanych danych wejściowych.

Znalezienie złożoności złożonych funkcji?

W poprzednich przykładach mieliśmy dość proste funkcje na wejściu. Jak jednak obliczyć Big-O funkcji, które wywołują (wielokrotne) inne funkcje na wejściu?

Spójrzmy:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

W powyższym skrypcie wykonywanych jest kilka zadań, najpierw ciąg znaków jest drukowany na konsoli 5 razy za pomocą print oświadczenie. Następnie dwukrotnie wypisujemy listę wejściową na ekranie, a na końcu kolejny ciąg jest wypisywany trzy razy na konsoli. Aby znaleźć złożoność takiego algorytmu, musimy rozbić kod algorytmu na części i spróbować znaleźć złożoność poszczególnych elementów. Zaznacz złożoność każdego elementu.

W pierwszej sekcji mamy:

for i in range(5):
	print("Python is awesome")

Złożoność tej części to O (5) ponieważ w tym fragmencie kodu wykonywanych jest pięć stałych kroków, niezależnie od danych wejściowych.

Dalej mamy:

for item in items:
	print(item)

Wiemy, że złożoność powyższego fragmentu kodu jest Na). Podobnie złożoność następującego fragmentu kodu jest również Na):

for item in items:
	print(item)

Wreszcie, w poniższym fragmencie kodu, łańcuch jest wypisywany trzy razy, stąd złożoność wynosi O (3):

print("Big O")
print("Big O")
print("Big O")

Aby znaleźć ogólną złożoność, musimy po prostu dodać te indywidualne złożoności:

O(5) + O(n) + O(n) + O(3)

Upraszczając powyższe otrzymujemy:

O(8) + O(2n) = O(8+2n)

Powiedzieliśmy wcześniej, że kiedy wejście (które w tym przypadku ma długość n) staje się bardzo duże, stałe stają się nieistotne, tj. dwa lub połowa nieskończoności nadal pozostaje nieskończonością. Dlatego możemy zignorować stałe. Ostateczna złożoność algorytmu będzie Na)!

Najgorsza a najlepsza złożoność przypadku

Zwykle, gdy ktoś pyta Cię o złożoność algorytmu – interesuje go złożoność najgorszego przypadku (Big-O). Czasami mogą być również zainteresowani złożonością najlepszego przypadku (Big-Omega).

Aby zrozumieć związek między nimi, spójrzmy na inny fragment kodu:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

W powyższym skrypcie mamy funkcję, która pobiera liczbę i listę liczb jako dane wejściowe. Zwraca true, jeśli podana liczba znajduje się na liście liczb, w przeciwnym razie zwraca None. Jeśli wyszukasz 2 na liście, zostanie ono znalezione w pierwszym porównaniu. Jest to najlepszy przypadek złożoności algorytmu polegający na tym, że poszukiwany element znajduje się w pierwszym przeszukiwanym indeksie. Najlepsza złożoność przypadku, w tym przypadku jest O (1). Z drugiej strony, jeśli wyszukasz 10, zostanie on znaleziony w ostatnio wyszukiwanym indeksie. Algorytm będzie musiał przeszukać wszystkie pozycje na liście, stąd złożoność najgorszego przypadku staje się Na).

Oprócz złożoności najlepszego i najgorszego przypadku możesz również obliczyć średnia złożoność (Big-Theta) algorytmu, który mówi „przy losowym wejściu, jaka jest oczekiwana złożoność czasowa algorytmu”?

Złożoność przestrzeni

Oprócz złożoności czasowej, gdzie liczysz liczbę kroków wymaganych do wykonania algorytmu, możesz również znaleźć złożoność przestrzeni co odnosi się do ilości miejsca, które musisz przydzielić w pamięci podczas wykonywania programu.

Spójrz na następujący przykład:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

Połączenia return_squares() funkcja przyjmuje listę liczb całkowitych i zwraca listę z odpowiednimi kwadratami. Algorytm musi przydzielić pamięć na taką samą liczbę pozycji, jak na liście wejść. Dlatego złożoność przestrzenna algorytmu staje się Na).

Wnioski

Notacja Big-O to standardowa metryka używana do pomiaru złożoności algorytmu. W tym przewodniku zbadaliśmy, czym jest notacja Big-O i jak można ją wykorzystać do pomiaru złożoności różnych algorytmów. Przebadaliśmy również różne typy funkcji Big-O za pomocą różnych przykładów w Pythonie. Na koniec krótko omówiliśmy złożoność najgorszego i najlepszego przypadku wraz ze złożonością przestrzeni.