Matematycy rzucają kostką i zdobywają papier-kamień-nożyce

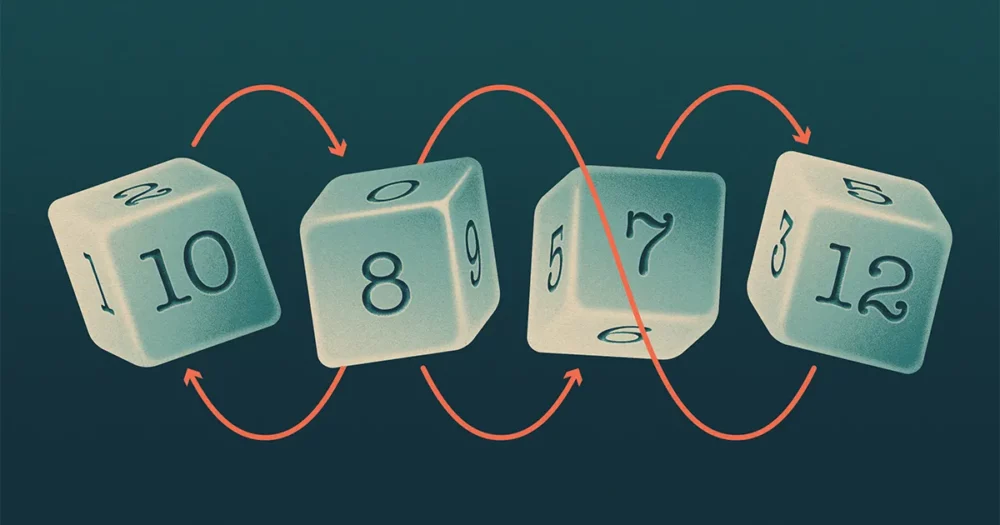
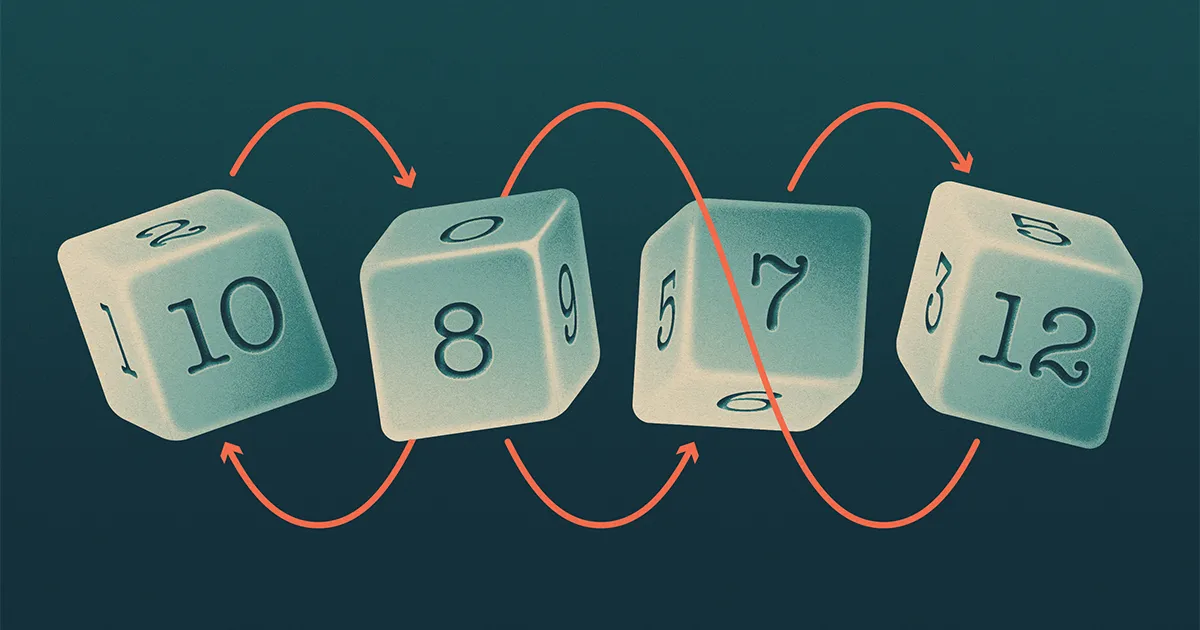
Jak opowiada Bill Gates, Warren Buffett wyzwał go kiedyś do gry w kości. Każdy wybierał jedną z czterech kości należących do Buffetta, a następnie rzucał, z wyższą liczbą wygrywającą. To nie były standardowe kości — miały inny zestaw liczb niż zwykle od 1 do 6. Buffett zaproponował, że Gates wybierze jako pierwszy, aby mógł wybrać najsilniejszą kość. Ale po tym, jak Gates zbadał kości, przedstawił kontrpropozycję: Buffett powinien wybrać pierwszy.

Gates zauważył, że kości Buffetta mają dziwną właściwość: żadna z nich nie była najsilniejsza. Gdyby Gates wybrał jako pierwszy, to niezależnie od tego, którą kość wybrałby, Buffett byłby w stanie znaleźć inną kość, która mogłaby ją pokonać (to znaczy taką, która ma ponad 50% szans na wygraną).

Cztery kości Buffetta (nazwijcie je A, B, C i D) utworzyły wzór przypominający kamień-papier-nożyce, w którym A uderzeń B, B uderzeń C, C uderzeń D i D uderzeń A. Matematycy twierdzą, że taki zestaw kości jest „nieprzechodni”.

„To wcale nie jest intuicyjne, że [nieprzechodnie kości] powinny w ogóle istnieć” – powiedział Briana Conreya, dyrektor Amerykańskiego Instytutu Matematyki (AIM) w San Jose, który napisał wpływowy artykuł na ten temat w 2013 roku.

Matematycy wymyślili tzw pierwsze przykłady nieprzechodnich kości ponad 50 lat temu i ostatecznie okazały że biorąc pod uwagę kości o coraz większej liczbie boków, możliwe jest tworzenie nieprzechodnich cykli o dowolnej długości. Do niedawna matematycy nie wiedzieli, jak powszechne są kości nieprzechodnie. Czy musisz starannie wymyślać takie przykłady, czy możesz wybrać losowo kości i mieć dobrą szansę na znalezienie zbioru nieprzechodniego?

Patrząc na trzy kości, jeśli to wiesz A uderzeń B i B uderzeń C, to wydaje się dowodem na to A jest najsilniejszy; sytuacje gdzie C uderzeń A powinno być rzadkie. I rzeczywiście, jeśli pozwolimy, aby liczby na kostkach sumowały się do różnych sum, to matematycy uważają, że ta intuicja jest prawdziwa.

Ale a artykuł opublikowany w Internecie pod koniec ubiegłego roku pokazuje, że w innym naturalnym środowisku ta intuicja zawodzi spektakularnie. Załóżmy, że wymagasz, aby twoje kości używały tylko liczb, które pojawiają się na zwykłej kości i miały taką samą sumę jak zwykła kość. Następnie gazeta pokazała, jeśli A uderzeń B i B uderzeń C, A i C mają zasadniczo równe szanse na zwycięstwo nad sobą.

"Wiedząc to A uderzeń B i B uderzeń C po prostu nie podaje informacji o tym, czy A uderzeń C, "Powiedział Timothy Gowers z University of Cambridge, medalista Fields i jeden z współtwórców nowego wyniku, który został udowodniony poprzez otwartą współpracę online znaną jako projekt Polymath.

Tymczasem kolejny Ostatni artykuł analizuje zestawy czterech lub więcej kości. To odkrycie jest prawdopodobnie jeszcze bardziej paradoksalne: jeśli na przykład wybierzesz losowo cztery kości i stwierdzisz, że A uderzeń B, B uderzeń C i C uderzeń D, to już trochę jeszcze prawdopodobnie dla D pobić A niż na odwrót.

Ani Silny, ani Słaby

Niedawny wysyp wyników zaczął się mniej więcej dziesięć lat temu, po tym jak Conrey wziął udział w spotkaniu dla nauczycieli matematyki z sesją poświęconą nieprzechodnim kościom. „Nie miałem pojęcia, że ​​takie rzeczy mogą istnieć” – powiedział. „Zafascynowałem się nimi”.

Zdecydował (później dołączył do niego kolega Kenta Morrisona w AIM), aby zbadać ten temat z trzema licealistami, których był mentorem — Jamesem Gabbardem, Katie Grant i Andrew Liu. Jak często, zastanawiała się grupa, losowo wybrane kości tworzą nieprzechodni cykl?

Uważa się, że nieprzechodnie zestawy kości są rzadkie, jeśli numery kostek sumują się do różnych sum, ponieważ kość z najwyższą sumą prawdopodobnie pokona pozostałe. Zespół postanowił więc skoncentrować się na kościach, które mają dwie właściwości: po pierwsze, kości używają tych samych liczb, co na standardowej kości — od 1 do n, w przypadku ndwustronna kostka. A po drugie, numery twarzy sumują się do tej samej sumy, co na standardowej kości. Ale w przeciwieństwie do standardowych kości, każda kość może powtarzać niektóre liczby i pomijać inne.

W przypadku kości sześciościennych istnieją tylko 32 różne kości, które mają te dwie właściwości. Tak więc przy pomocy komputera zespół mógł zidentyfikować wszystkie trójki, w których A uderzeń B i B uderzeń C. Naukowcy ku swemu zdumieniu stwierdzili, że A uderzeń C w 1,756 trójkach i C uderzeń A w 1,731 potrójnych — prawie identycznych liczbach. Opierając się na tych obliczeniach i symulacjach kostek o więcej niż sześciu bokach, domyślił się zespół że gdy liczba ścianek na kostce zbliża się do nieskończoności, prawdopodobieństwo, że A uderzeń C zbliża się do 50%.

Przypuszczenie, z jego mieszanką dostępności i niuansów, wydało się Conreyowi dobrą pożywką dla projektu Polymath, w którym wielu matematyków spotyka się online, aby dzielić się pomysłami. W połowie 2017 roku zaproponował pomysł Gowersowi, twórcy podejścia Polymath. „Bardzo podobało mi się to pytanie ze względu na jego zaskakującą wartość” — powiedział Gowers. napisał a blogu o przypuszczeniu, które wywołało lawinę komentarzy, aw ciągu sześciu dodatkowych postów komentatorom udało się to udowodnić.

W swoim artykule umieszczone w Internecie pod koniec listopada 2022 r. kluczowa część dowodu polegała na wykazaniu, że w większości nie ma sensu mówić o tym, czy pojedyncza kość jest silna, czy słaba. Kości Buffetta, z których żadna nie jest najmocniejsza z paczki, nie są takie niezwykłe: jeśli losowo wybierzesz kość, jak pokazał projekt Polymath, prawdopodobnie pokona około połowy pozostałych kości i przegra z drugą połową. „Prawie każda kość jest dość przeciętna” – powiedział Gowers.

Projekt odbiegał od pierwotnego modelu zespołu AIM pod jednym względem: aby uprościć niektóre kwestie techniczne, projekt zadeklarował, że kolejność liczb na kostce ma znaczenie — na przykład 122556 i 152562 będą uważane za dwie różne kostki. Ale wynik Polymath, w połączeniu z eksperymentalnymi dowodami zespołu AIM, stwarza silne przypuszczenie, że przypuszczenie jest również prawdziwe w oryginalnym modelu, powiedział Gowers.

„Byłem absolutnie zachwycony, że wymyślili ten dowód” – powiedział Conrey.

Jeśli chodzi o kolekcje czterech lub więcej kości, zespół AIM przewidział podobne zachowanie do trzech kości: na przykład, jeśli A uderzeń B, B uderzeń C i C uderzeń D wtedy powinno być około 50-50 prawdopodobieństwa D uderzeń A, zbliżając się dokładnie do 50-50, gdy liczba ścianek na kostce zbliża się do nieskończoności.

Aby przetestować to przypuszczenie, naukowcy przeprowadzili symulację bezpośrednich turniejów dla zestawów czterech kości z 50, 100, 150 i 200 bokami. Symulacje nie były zgodne z ich przewidywaniami tak dokładnie, jak w przypadku trzech kostek, ale wciąż były wystarczająco bliskie, aby wzmocnić ich wiarę w przypuszczenie. Ale chociaż naukowcy nie zdawali sobie z tego sprawy, te małe rozbieżności niosły ze sobą inną wiadomość: w przypadku zestawów czterech lub więcej kości ich przypuszczenia są fałszywe.

„Naprawdę chcieliśmy, aby [przypuszczenie] było prawdziwe, ponieważ byłoby fajnie” – powiedział Conrey.

W przypadku czterech kostek Elżbieta Kornacchia Szwajcarskiego Federalnego Instytutu Technologii w Lozannie i Jana Hązły z Afrykańskiego Instytutu Nauk Matematycznych w Kigali w Rwandzie, pokazał w papier opublikował online pod koniec 2020 r., że jeśli A uderzeń B, B uderzeń C i C uderzeń D, następnie D ma nieco większą niż 50% szansę na pokonanie A — prawdopodobnie około 52%, powiedział Hązła. (Podobnie jak w artykule Polymath, Cornacchia i Hązła zastosowali nieco inny model niż w artykule AIM.)

Odkrycie Cornacchii i Hązły wynika z faktu, że choć z reguły pojedyncza kość nie będzie ani silna, ani słaba, to para kości może czasem mieć wspólne obszary siły. Jeśli wybierzesz losowo dwie kości, pokazali Cornacchia i Hązła, istnieje spore prawdopodobieństwo, że kości będą skorelowane: będą miały tendencję do wygrywania lub przegrywania z tymi samymi kośćmi. – Jeśli poproszę o utworzenie dwóch zbliżonych do siebie kostek, okazuje się, że jest to możliwe – mówi Hązła. Te małe obszary korelacji odsuwają wyniki turniejów od symetrii, gdy tylko na obrazie pojawią się co najmniej cztery kości.

Ostatnie artykuły to nie koniec historii. Artykuł Cornacchii i Hązły dopiero zaczyna odkrywać dokładnie, w jaki sposób korelacje między kostkami zaburzają równowagę symetrii turniejów. W międzyczasie wiemy jednak, że istnieje wiele zestawów nieprzechodnich kości — może nawet taki, który jest na tyle subtelny, że skłoni Billa Gatesa do wybrania pierwszego.