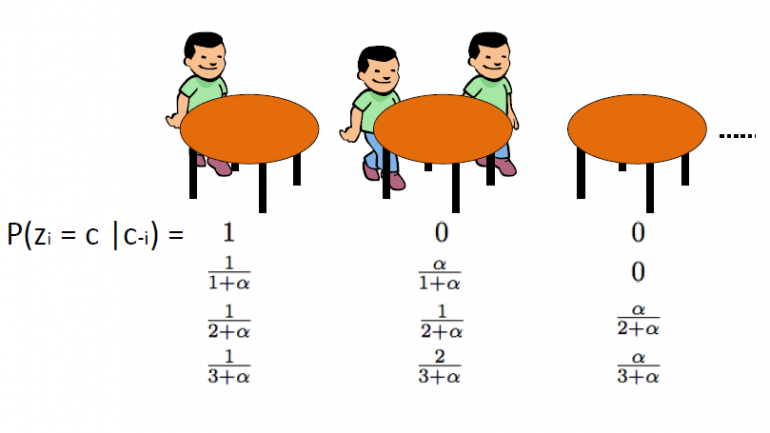The Dirichlet Process the Chinese Restaurant Process i inne oświadczenia

• 20 maja 2014 r.
• Wasilis Wryniotis
• . Bez komentarza

Ten artykuł jest trzecią częścią serii poświęconej klastrowaniu za pomocą modeli mieszanin procesowych Dirichleta. Poprzednim razem zdefiniowaliśmy Model Mieszaniny Skończonej w oparciu o Rozkład Dirichleta i zadaliśmy pytania, w jaki sposób możemy uczynić ten konkretny model nieskończonym. Pokrótce omówiliśmy pomysł przyjęcia granicy modelu, gdy liczba k skupień dąży do nieskończoności, ale jak podkreśliliśmy, istnienie takiego obiektu nie jest trywialne (innymi słowy, jak właściwie „przyjąć granicę modelu ”?). Przypominamy, że powodem, dla którego chcemy uczynić k nieskończonym, jest to, że w ten sposób otrzymamy model nieparametryczny, który nie wymaga od nas predefiniowania całkowitej liczby klastrów w danych.

Aktualizacja: Platforma uczenia maszynowego Datumbox jest teraz open-source i bezpłatna pobieranie. Zapoznaj się z pakietem com.datumbox.framework.machinelearning.clustering, aby zobaczyć implementację modeli mieszania procesów Dirichleta w Javie.

Chociaż naszym celem jest zbudowanie modelu, który jest w stanie wykonać klastrowanie na zestawach danych, przed tym musimy omówić procesy Dirichleta. Podamy zarówno ścisłe definicje matematyczne, jak i bardziej intuicyjne wyjaśnienia DP oraz omówimy sposoby konstruowania procesu. Te konstrukcje/reprezentacje mogą być postrzegane jako sposób na znalezienie wystąpień procesu Dirichleta w „prawdziwym życiu”.

Pomimo tego, że starałem się dostosować mój raport badawczy w taki sposób, aby te wpisy na blogu były łatwiejsze do śledzenia, nadal ważne jest zdefiniowanie niezbędnych narzędzi matematycznych i rozkładów, zanim przejdziemy do korzystania z modeli. Modele procesu Dirichleta są przedmiotem aktywnych badań, ale wymagają one dobrego zrozumienia statystyki i procesów stochastycznych przed ich użyciem. Innym problemem jest to, że jak zobaczymy w tym artykule, procesy Dirichleta mogą być reprezentowane/konstruowane na wiele sposobów. W rezultacie kilka artykułów naukowych używa zupełnie innej notacji/konwencji i bada problem z różnych punktów widzenia. W tym poście staram się je jak najprościej wyjaśnić i używać tej samej notacji. Mamy nadzieję, że sprawa stanie się jaśniejsza dzięki dwóm nadchodzącym artykułom, które skupiają się na definicji modeli mieszania procesów Dirichleta oraz na tym, jak faktycznie ich używać do przeprowadzania analizy skupień.

1. Definicja procesu Dirichleta

Proces Dirichleta w przestrzeni Θ jest procesem stochastycznym. Jest to rozkład prawdopodobieństwa nad „rozkładami prawdopodobieństwa w przestrzeni Θ” oraz a czerpać z niego jest dyskretną dystrybucją. Bardziej formalnie rozkład Dirichleta jest rozkładem na miarach prawdopodobieństwa. A miara prawdopodobieństwa jest funkcją podzbiorów przestrzeni Θ do [0,1]. G jest miarą losowego prawdopodobieństwa o rozkładzie DP, oznaczoną jako , jeśli dla dowolnej partycji (A₁,…A_n) przestrzeni Θ mamy to .

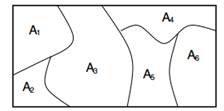
Rysunek 1: Marginesy na skończonych partycjach mają rozkład Dirichleta.

DP ma dwa parametry: Pierwszy to rozkład bazowy G₀ który służy jak środek . Drugi to parametr siły α, który jest ściśle dodatni i działa jak odwrotna wariancja . Określa stopień powtarzalności wartości rozkładu produkcji. Im wyższa wartość a, tym mniejsze powtórzenie; im mniejsza wartość, tym większa powtarzalność wartości rozkładu produkcji. Wreszcie przestrzeń Θ jest przestrzenią parametrów, na której definiujemy DP. Ponadto przestrzeń Θ jest również przestrzenią definicji G₀ który jest taki sam jak G.

Prostsze i więcej intuicyjny sposób wyjaśnienie procesu Dirichleta jest następujące. Załóżmy, że mamy przestrzeń Θ, którą można podzielić w dowolny skończony sposób (A₁,…,A_n) oraz rozkład prawdopodobieństwa G, który przypisuje im prawdopodobieństwa. G to określony rozkład prawdopodobieństwa na Θ, ale istnieje wiele innych. Proces Dirichleta na Θ modeluje dokładnie to; jest to rozkład po wszystkich możliwych rozkładach prawdopodobieństwa na przestrzeni Θ. Proces Dirichleta jest parametryzowany za pomocą G₀ funkcja bazowa i parametr stężenia α. Możemy powiedzieć, że G rozkłada się zgodnie z DP o parametrach α i G₀ jeśli łączny rozkład prawdopodobieństw, które G przypisuje podziałom Θ, jest zgodny z rozkładem Dirichleta. Alternatywnie możemy powiedzieć, że prawdopodobieństwa, które G przypisuje dowolnemu skończonemu podziałowi Θ, są zgodne z rozkładem Dirichleta.

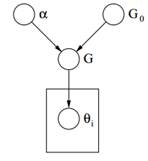
Rysunek 2: Graficzny model procesu Dirichleta

Wreszcie powyżej możemy zobaczyć graficzny model DP. Należy zauważyć, że α jest hiperparametrem skalarnym, G₀ jest rozkładem bazowym DP, G losowym rozkładem w przestrzeni parametrów Θ pobranym z DP, który przypisuje prawdopodobieństwa parametrom i θ_i jest wektorem parametrów, który jest pobierany z rozkładu G i jest elementem przestrzeni Θ.

2. Tylne procesy Dirichleta

Procesy tylnego Dirichleta zostały omówione przez: Ferguson. Zaczynamy od losowej miary prawdopodobieństwa G z procesu Dirichleta, . Ponieważ G jest rozkładem prawdopodobieństwa nad Θ, możemy również próbkować z tego rozkładu i wylosować niezależne próbki o identycznym rozkładzie θ₁,…,_n ~ G. Ponieważ losowania z procesu Dirichleta są rozkładami dyskretnymi, możemy reprezentować gdzie to skrót od która jest funkcją delta przyjmującą 1 jeśli i 0 gdzie indziej. Ciekawym efektem tego jest to, że skoro G jest zdefiniowane w ten sposób, istnieje dodatnie prawdopodobieństwo, że różne próbki mają tę samą wartość . Jak zobaczymy później, tworzy to efekt grupowania, który można wykorzystać do przeprowadzenia analizy skupień na zestawach danych.

Korzystając z powyższych definicji i obserwacji, chcemy oszacować awersję procesu Dirichleta, biorąc pod uwagę próbki θ. Niemniej jednak, skoro wiemy, że i używając reguł Bayesa i koniugatu między Dirichletem a wielomianem, mamy to i .

Równanie 1: Tylny proces Dirichleta

Ta właściwość jest bardzo ważna i jest używana przez różne reprezentacje DP.

3. Reprezentacje procesu Dirichleta

W poprzednich segmentach zdefiniowaliśmy proces Dirichleta i przedstawiliśmy jego model teoretyczny. Jedno ważne pytanie, na które musimy odpowiedzieć, to skąd wiemy, że taki obiekt istnieje i jak możemy? konstruować i reprezentować proces Dirichleta.

Pierwsze oznaki istnienia dostarczyli: Ferguson który zastosował twierdzenie Kołmogorowa o spójności, podał definicję procesu Dirichleta i opisał proces Dirichleta tylnego. Kontynuując swoje badania, Blackwell i MacQueen wykorzystał twierdzenie de Finetti do udowodnienia istnienia takiej losowej miary prawdopodobieństwa i wprowadził schemat urny Blackwella-MacQueena, który spełnia właściwości procesu Dirichleta. W 1994 Sethuramana zapewnił dodatkowy prosty i bezpośredni sposób konstruowania DP poprzez wprowadzenie konstrukcji łamacza kijów. Wreszcie inną reprezentację przedstawiła Aldous który wprowadził chiński proces restauracyjny jako skuteczny sposób na skonstruowanie procesu Dirichleta.

Różne reprezentacje procesu Dirichleta są matematycznie równoważne, ale ich sformułowanie różni się, ponieważ badają problem z różnych punktów widzenia. Poniżej przedstawiamy najczęstsze reprezentacje występujące w literaturze i koncentrujemy się na chińskim procesie restauracyjnym, który zapewnia prosty i wydajny obliczeniowo sposób konstruowania algorytmów wnioskowania dla procesu Dirichleta.

3.1 Schemat urny Blackwella-MacQueena

Schemat urny Blackwella-MacQueena może być użyty do reprezentowania procesu Dirichleta i został wprowadzony przez Blackwell i MacQueen. Opiera się na schemacie urny Pólya, który można uznać za odwrotny model pobierania próbek bez wymiany. W schemacie urny Pólya zakładamy, że mamy nieprzezroczystą urnę zawierającą kolorowe kulki i losujemy kulki. Kiedy rysujemy kulkę, obserwujemy jej kolor, wkładamy ją z powrotem do urny i dokładamy dodatkową kulkę w tym samym kolorze. Podobny schemat jest używany przez Blackwella i MacQueena do skonstruowania procesu Dirichleta.

Ten schemat tworzy sekwencję θ₁,₂,… z prawdopodobieństwa warunkowe . W tym schemacie zakładamy, że G₀ to rozkład na kolory i każdy θ_n reprezentuje kolor kuli umieszczonej w urnie. ten algorytm jest następujący:

· Zaczynamy od pustej urny.

· Z prawdopodobieństwem proporcjonalnym do α rysujemy i dodajemy kulę tego koloru w urnie.

· Z prawdopodobieństwem proporcjonalnym do n-1 losujemy kulkę z urny, obserwujemy jej kolor, kładziemy ją z powrotem do urny i dodajemy do niej dodatkową kulkę tego samego koloru.

Wcześniej zaczęliśmy od procesu Dirichleta i wyprowadziliśmy schemat Blackwella-MacQueena. Teraz zacznijmy odwrotnie od schematu Blackwella-MacQueena i wyprowadźmy DP. Od θ_i zostały narysowane w iid sposób z G, ich łączny rozkład będzie niezmienny w stosunku do wszelkich skończonych permutacji, a zatem są wymienne. W związku z tym, używając twierdzenia de Finettiego, dowiadujemy się, że musi istnieć podział na miary, aby były one iid i ten rozkład jest procesem Dirichleta. W efekcie udowadniamy, że schemat urny Blackwella-MacQueena jest reprezentacją DP i daje nam konkretny sposób na jego skonstruowanie. Jak zobaczymy później, schemat ten jest matematycznie odpowiednikiem chińskiego procesu restauracyjnego.

3.2 Konstrukcja łamiąca patyki

Konstrukcja łamania patyków jest alternatywnym sposobem przedstawienia procesu Dirichleta, który został wprowadzony przez Sethuramana. Jest to konstruktywny sposób kształtowania dystrybucja i wykorzystuje po analogii: Zakładamy, że mamy kij o długości 1, łamiemy go w pozycji β₁ i przypisujemy π₁ równa długości części kija, którą złamaliśmy. Powtarzamy ten sam proces, aby uzyskać π₂, Liczba Pi₃…itp; ze względu na sposób, w jaki ten schemat jest zdefiniowany, możemy kontynuować to nieskończenie wiele razy.

Na podstawie powyższego π_k można modelować jako , Gdzie podczas gdy jak w poprzednich schematach θ są próbkowane bezpośrednio przez rozkład Base . W konsekwencji rozkład G można zapisać jako sumę funkcji delta ważonych π_k prawdopodobieństwa równe . W ten sposób konstrukcja łamania patyków daje nam prosty i intuicyjny sposób na skonstruowanie procesu Dirichleta.

3.3 Proces chińskiej restauracji

Chiński proces restauracyjny, który został wprowadzony przez Aldous, jest kolejnym skutecznym sposobem przedstawienia procesu Dirichleta i może być bezpośrednio powiązany ze schematem urny Blackwella-MacQueena. Ten schemat wykorzystuje po analogii: Zakładamy, że istnieje chińska restauracja z nieskończoną liczbą stołów. Gdy klienci wchodzą do restauracji, siadają losowo do dowolnego zajętego stolika lub decydują się usiąść przy pierwszym wolnym wolnym stole.

CRP określa rozkład na przestrzeni przegród liczb całkowitych dodatnich. Zaczynamy od rysowania θ₁,… θ_n ze schematu urny Blackwell-MacQueen. Jak omówiliśmy w poprzednich segmentach, spodziewamy się efektu grupowania, a zatem całkowita liczba unikalnych wartości θ k będzie znacznie mniejsza niż n. To definiuje podział zbioru {1,2,…,n} na k skupień. W konsekwencji czerpanie ze schematu urny Blackwella-MacQueena indukuje losowy podział zbioru {1,2,…,n}. Proces chińskiej restauracji jest tym indukowany dystrybucja na partycje. Algorytm wygląda następująco:

· Zaczynamy od pustej restauracji.

· 1^st klient siedzi zawsze na 1^st stół

· n+1^th klient ma 2 opcje:

o Usiądź na pierwszym wolnym stole z prawdopodobieństwem

o Usiądź z prawdopodobieństwem na dowolnym z k-tych zajętych stolików
gdzie jest liczba osób siedzących na tym stole

Gdzie α jest wartością dyspersji DP, a n jest całkowitą liczbą klientów w restauracji w danym czasie. Utajona zmienna z_i przechowuje numer tabeli i^th klient i przyjmuje wartości od 1 do k_n gdzie k_n to łączna liczba zajętych stolików, gdy w restauracji przebywa n klientów. Powinniśmy zauważyć, że k_n zawsze będzie mniejsze lub równe n i średnio wynosi około . Na koniec należy zauważyć, że prawdopodobieństwo ułożenia stołu jest niezmienna względem permutacji. Tak więc z_i jest wymienny, co oznacza, że ​​stoły o tej samej wielkości klientów mają to samo prawdopodobieństwo.

Proces Restauracji Chińskiej jest silnie powiązany ze schematem urn Pólya i Procesem Dirichleta. CRP to sposób na określenie dystrybucja na partycje (przypisania tablicowe) n punktów i mogą być używane jako a priori na przestrzeni zmiennej latentnej z_i który określa przypisania klastrów. CRP jest odpowiednikiem schematu urn Pólyi z tą różnicą, że nie przypisuje parametrów do każdej tabeli/klastra. Iść od CRP do schematu urny Poly rysujemy dla wszystkich tabel k=1,2… a następnie dla każdego x_i który jest zgrupowany w tabeli z_i przypisz . Innymi słowy przypisz do nowego x_i parametr θ tabeli. Wreszcie od nie możemy przypisać θ do nieskończonych tabel od samego początku, możemy po prostu przypisać nowe θ za każdym razem, gdy ktoś siada na nowym stole. W związku z powyższym CRP może pomóc nam w tworzeniu wydajnych obliczeniowo algorytmów do wykonywania analizy skupień na zbiorach danych.

W tym poście omówiliśmy proces Dirichleta i kilka sposobów jego skonstruowania. Powyższe pomysły wykorzystamy w następnym artykule. Wprowadzimy model mieszaniny procesu Dirichleta i użyjemy reprezentacji chińskiej restauracji w celu skonstruowania procesu Dirichleta i wykonania analizy skupień. Jeśli przegapiłeś kilka punktów, nie martw się, ponieważ w kolejnych dwóch artykułach wszystko stanie się jaśniejsze.

Mam nadzieję, że ten post Cię zainteresował. Jeśli tak, poświęć chwilę na udostępnienie go na Facebooku i Twitterze. 🙂.