Wykorzystanie sztucznej inteligencji do rozwiązania gry 2048 (kod JAVA)

• 7 kwietnia 2014 r.
• Wasilis Wryniotis
• . 6 komentarzy

Do tej pory większość z was słyszała / grała w 2048 gra przez Gabriele Cirulli. Jest to prosta, ale bardzo wciągająca gra planszowa, która wymaga łączenia liczb komórek w celu uzyskania liczby 2048. Zgodnie z oczekiwaniami, trudność gry rośnie, gdy więcej komórek jest wypełnionych wysokimi wartościami. Osobiście, chociaż spędziłem sporo czasu grając w tę grę, nigdy nie byłem w stanie osiągnąć 2048. Więc naturalną rzeczą jest próba opracowania solwera AI w JAVA, aby pokonać grę 2048. 🙂

W tym artykule pokrótce omówię moje podejście do budowania rozwiązania sztucznej inteligencji Game 2048, opiszę heurystykę, z której korzystałem i przedstawię pełny kod, który jest napisany w języku JAVA. Kod jest open source na licencji GPL v3 i można go pobrać z Github.

Tworzenie gry 2048 w JAVA

Oryginalna gra jest napisana w JavaScript, więc musiałem przepisać ją w JAVA od podstaw. Główną ideą gry jest to, że masz siatkę 4 × 4 z wartościami całkowitymi, z których wszystkie mają potęgi 2. Komórki o zerowej wartości są uważane za puste. W każdym momencie gry możesz przesuwać wartości w 4 kierunkach w górę, w dół, w prawo lub w lewo. Kiedy wykonujesz ruch, wszystkie wartości siatki przesuwają się w tym kierunku i zatrzymują się, gdy osiągną granice siatki lub gdy dotrą do innej komórki o wartości niezerowej. Jeśli ta poprzednia komórka ma tę samą wartość, dwie komórki są łączone w jedną komórkę z podwójną wartością. Na koniec każdego ruchu na planszę w jednej z pustych komórek dodawana jest losowa wartość, która wynosi 2 z prawdopodobieństwem 0.9 lub 4 z prawdopodobieństwem 0.1. Gra kończy się, gdy graczowi uda się stworzyć komórkę o wartości 2048 (wygrana) lub gdy nie ma innych ruchów do wykonania (przegrana).

W oryginalnej implementacji gry algorytm move-merge jest nieco skomplikowany, ponieważ bierze pod uwagę wszystkie kierunki. Ładne uproszczenie algorytmu można przeprowadzić, ustalając kierunek, w którym możemy łączyć elementy i odpowiednio obracać szachownicę, aby wykonać ruch. Mauritsa van der Schee napisał niedawno artykuł na ten temat, który moim zdaniem jest wart przeczytania.

Wszystkie klasy są udokumentowane komentarzami Javadoc. Poniżej przedstawiamy ogólny opis architektury realizacji:

1. Klasa zarządu

Klasa planszowa zawiera główny kod gry, który jest odpowiedzialny za przesuwanie pionków, obliczanie wyniku, sprawdzanie zakończenia gry itp.

2. Stan akcji i kierunek Wyliczenie

ActionStatus i Direction to 2 podstawowe wyliczenia, które odpowiednio przechowują wynik ruchu i jego kierunek.

3. Klasa ConsoleGame

ConsoleGame to główna klasa, która pozwala nam zagrać w grę i przetestować dokładność AI Solver.

4. Klasa AIsolver

AIsolver to podstawowa klasa modułu sztucznej inteligencji, która jest odpowiedzialna za ocenę następnego najlepszego posunięcia dla danej tablicy.

Techniki sztucznej inteligencji: przycinanie Minimax vs Alpha-beta

Opublikowano kilka podejść do automatycznego rozwiązania tej gry. Najbardziej godnym uwagi jest ten opracowany przez Matta Overlana. Aby rozwiązać problem, wypróbowałem dwa różne podejścia, używając algorytmu Minimax i używając przycinania alfa-beta.

Algorytm Minimax

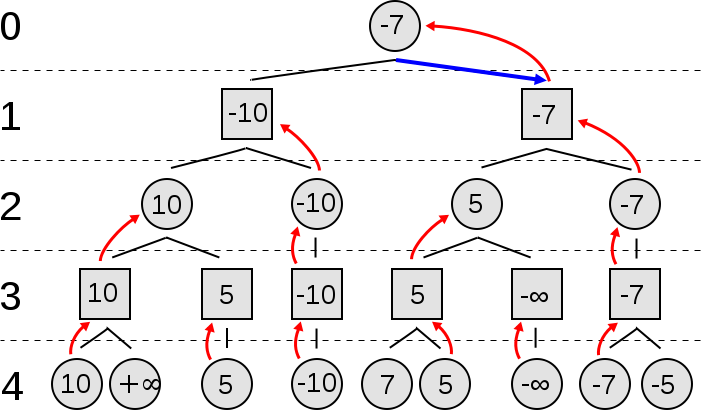
Połączenia Minimax to algorytm rekurencyjny, który może być używany do rozwiązywania gier dwuosobowych o sumie zerowej. W każdym stanie gry przypisujemy wartość. Algorytm Minimax przeszukuje przestrzeń możliwych stanów gry, tworząc drzewo, które jest rozwijane, aż osiągnie określoną, predefiniowaną głębokość. Po osiągnięciu tych stanów liścia ich wartości są używane do oszacowania stanów z węzłów pośrednich.

Ciekawym pomysłem tego algorytmu jest to, że każdy poziom reprezentuje turę jednego z dwóch graczy. Aby wygrać, każdy gracz musi wybrać ruch, który minimalizuje maksymalną wypłatę przeciwnika. Oto ładna prezentacja wideo algorytmu minimaks:

[Osadzone treści]

Poniżej możesz zobaczyć pseudokod Algorytmu Minimax:

funkcjonować minimax (węzeł, głębokość, maksymalizacjaPlayer)
    if głębokość = 0 or węzeł jest węzłem końcowym
        powrót heurystyczna wartość node
    if maximizingPlayer bestValue: = -∞
        dla każdego child of node val: = minimax (child, depth - 1, FALSE)) bestValue: = max (bestValue, val);
        powrót najlepsza wartość
    więcej
        bestValue: = + ∞
        dla każdego dziecko węzła val: = minimax (child, depth - 1, TRUE)) bestValue: = min (bestValue, val);
        powrót najlepsza wartość
(* Wstępne wezwanie do maksymalizacji gracza *)
minimax (początek, głębokość, PRAWDA)

Przycinanie alfa-beta

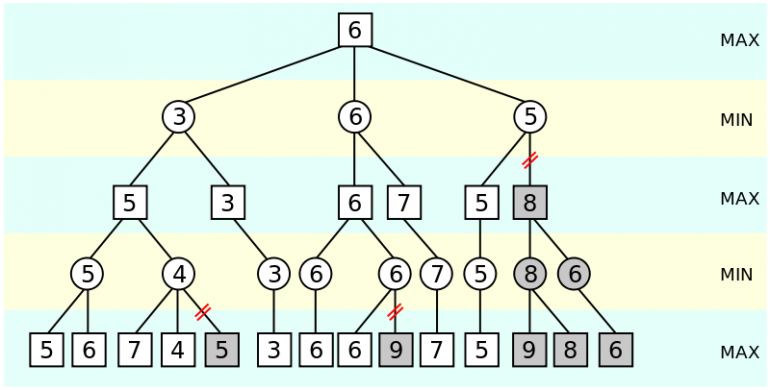
Połączenia Algorytm przycinania alfa-beta jest rozwinięciem minimaksu, które znacznie zmniejsza (przycina) liczbę węzłów, które musimy ocenić / rozszerzyć. Aby to osiągnąć, algorytm szacuje dwie wartości alfa i beta. Jeśli w danym węźle beta jest mniejsze niż alfa, wówczas pozostałe poddrzewa mogą zostać przycięte. Oto ładna prezentacja wideo algorytmu alfabety:

[Osadzone treści]

Poniżej możesz zobaczyć pseudokod algorytmu przycinania alfa-beta:

funkcjonować alphabeta (węzeł, głębokość, α, β, maksymalizacjaPlayer)
    if głębokość = 0 or węzeł jest węzłem końcowym
        powrót heurystyczna wartość node
    if Maksymalizowanie Gracza
        dla każdego dziecko węzła α: = max (α, alphabeta (child, depth - 1, α, β, FALSE))
            if β ≤ α
                złamać (* odcięcie β *)
        powrót α
    więcej
        dla każdego dziecko węzła β: = min (β, alphabeta (child, depth - 1, α, β, TRUE))
            if β ≤ α
                złamać (wartość odcięcia * α *)
        powrót β
(* Pierwsza rozmowa *)
alphabeta (początek, głębia, -∞, + ∞, PRAWDA)

W jaki sposób sztuczna inteligencja jest używana do rozwiązania Game 2048?

Aby skorzystać z powyższych algorytmów, musimy najpierw zidentyfikować dwóch graczy. Pierwszy gracz to osoba, która gra. Drugim graczem jest komputer, który losowo wstawia wartości do komórek planszy. Oczywiście pierwszy gracz stara się zmaksymalizować swój wynik i osiągnąć fuzję 2048. Z drugiej strony komputer w oryginalnej grze nie jest specjalnie zaprogramowany do blokowania użytkownika, wybierając dla niego najgorszy możliwy ruch, ale raczej losowo wstawia wartości do pustych komórek.

Dlaczego więc używamy technik sztucznej inteligencji, które rozwiązują gry o sumie zerowej i które w szczególności zakładają, że obaj gracze wybierają dla nich najlepszy możliwy ruch? Odpowiedź jest prosta; pomimo tego, że tylko pierwszy gracz stara się zmaksymalizować swój wynik, wybory komputera mogą zablokować postęp i uniemożliwić użytkownikowi ukończenie gry. Modelując zachowanie komputera jako ortologicznego nielosowego gracza, zapewniamy, że nasz wybór będzie solidny niezależnie od tego, w co gra komputer.

Drugą ważną częścią jest przypisanie wartości stanom gry. Ten problem jest stosunkowo prosty, ponieważ sama gra daje nam wynik. Niestety próba samodzielnego maksymalizowania wyniku nie jest dobrym podejściem. Jednym z powodów jest to, że pozycja wartości i liczba pustych komórek o wartościach pustych są bardzo ważne dla wygrania gry. Na przykład, jeśli rozproszymy duże wartości w odległych komórkach, byłoby nam naprawdę trudno je połączyć. Dodatkowo, jeśli nie mamy dostępnych pustych komórek, ryzykujemy przegraną w każdej chwili.

Ze wszystkich powyższych powodów kilka heurystyk zostały zasugerowane takie jak Monotyczność, gładkość i wolne płytki na planszy. Głównym zamysłem nie jest wykorzystanie samego wyniku do oceny każdego stanu gry, ale zamiast tego skonstruowanie heurystycznej oceny złożonej, która zawiera wspomniane wyżej wyniki.

Na koniec powinniśmy zauważyć, że chociaż opracowałem implementację algorytmu Minimax, duża liczba możliwych stanów powoduje, że algorytm jest bardzo powolny i dlatego konieczne jest przycinanie. W efekcie w implementacji JAVA wykorzystuję rozszerzenie algorytmu przycinania Alpha-beta. Dodatkowo, w przeciwieństwie do innych implementacji, nie przycinam agresywnie wyborów komputera używając dowolnych reguł, ale zamiast tego biorę je pod uwagę, aby znaleźć najlepszy możliwy ruch gracza.

Opracowanie heurystycznej funkcji punktacji

Aby przejść grę, wypróbowałem kilka różnych funkcji heurystycznych. Ten, który uważam za najbardziej przydatny, jest następujący:

private static int heuristicScore(int actualScore, int numberOfEmptyCells, int clusteringScore) {
     int score = (int) (actualScore+Math.log(actualScore)*numberOfEmptyCells -clusteringScore);
     return Math.max(score, Math.min(actualScore, 1));
}

Powyższa funkcja łączy rzeczywisty wynik planszy, liczbę pustych komórek / kafelków i metrykę zwaną wynikiem grupowania, którą omówimy później. Przyjrzyjmy się bardziej szczegółowo każdemu komponentowi:

1. Rzeczywisty wynik: Z oczywistych względów obliczając wartość planszy musimy wziąć pod uwagę jej ocenę. Tablice z wyższymi wynikami są na ogół preferowane w porównaniu z planszami z niższymi wynikami.
2. Liczba pustych komórek: Jak wspomnieliśmy wcześniej, utrzymanie kilku pustych komórek jest ważne, aby mieć pewność, że nie przegramy gry w następnych ruchach. Stany planszowe z większą liczbą pustych komórek są generalnie preferowane w porównaniu do innych, w których jest ich mniej. Powstaje pytanie, jak wycenilibyśmy te puste komórki? W moim rozwiązaniu ważę je według logarytmu rzeczywistego wyniku. Ma to następujący efekt: Im niższy wynik, tym mniej ważne jest posiadanie wielu pustych komórek (Dzieje się tak, ponieważ na początku gry łączenie komórek jest dość łatwe). Im wyższy wynik, tym ważniejsze jest upewnienie się, że w naszej grze mamy puste komórki (Dzieje się tak dlatego, że pod koniec gry bardziej prawdopodobne jest przegranie z powodu braku pustych komórek.
3. Wynik grupowania: Używamy wyniku grupowania, który mierzy, jak rozproszone są wartości naszej tablicy. Gdy komórki o podobnych wartościach są blisko siebie, łatwiej je połączyć, co oznacza, że ​​trudniej jest przegrać. W tym przypadku punktacja skupienia ma niską wartość. Jeśli wartości na planszy są rozproszone, ten wynik uzyskuje bardzo dużą wartość. Ten wynik jest odejmowany od poprzednich dwóch wyników i działa jak kara, która zapewnia, że ​​preferowane będą plansze grupowane.

W ostatnim wierszu funkcji upewniamy się, że wynik jest nieujemny. Wynik powinien być ściśle dodatni, jeśli wynik na tablicy jest dodatni, a zero tylko wtedy, gdy wynik na tablicy wynosi zero. Funkcje max i min są tak skonstruowane, że uzyskujemy ten efekt.

Na koniec powinniśmy zauważyć, że gdy gracz osiągnie stan gry końcowej i żadne dalsze ruchy nie są dozwolone, nie używamy powyższego wyniku do oszacowania wartości stanu. Jeśli gra jest wygrana, przypisujemy najwyższą możliwą wartość całkowitą, a jeśli gra jest przegrana, przypisujemy najniższą wartość nieujemną (0 lub 1 z podobną logiką jak w poprzednim akapicie).

Więcej o wyniku klastrowym

Jak powiedzieliśmy wcześniej, wynik grupowania mierzy, jak bardzo rozrzucone są wartości na planszy i działa jak kara. Skonstruowałem ten wynik w taki sposób, aby zawierał wskazówki / zasady od użytkowników, którzy „opanowali” grę. Pierwsza sugerowana zasada polega na tym, że starasz się trzymać komórki o podobnych wartościach blisko siebie, aby łatwiej je łączyć. Druga zasada mówi, że komórki o wysokiej wartości powinny znajdować się blisko siebie i nie pojawiać się na środku planszy, ale raczej na bokach lub rogach.

Zobaczmy, jak szacowany jest wynik grupowania. Dla każdej komórki tablicy szacujemy sumę bezwzględnych różnic w stosunku do jej sąsiadów (z wyłączeniem pustych komórek) i bierzemy średnią różnicę. Powodem, dla którego bierzemy średnie, jest unikanie liczenia więcej niż raz efektu dwóch sąsiadujących komórek. Całkowity wynik grupowania jest sumą wszystkich tych średnich.

Wynik grupowania ma następujące atrybuty:

1. Wysoką wartość uzyskuje, gdy wartości tablicy są rozproszone, a niską, gdy komórki o podobnych wartościach są blisko siebie.
2. Nie przeważa nad efektem dwóch sąsiednich komórek.
3. Komórki na marginesach lub rogach mają mniej sąsiadów, a tym samym niższe wyniki. W rezultacie, gdy wysokie wartości są umieszczone w pobliżu marginesów lub rogów, mają mniejsze wyniki, a tym samym kara jest mniejsza.

Dokładność algorytmu

Zgodnie z oczekiwaniami dokładność (czyli procent wygranych gier) algorytmu w dużej mierze zależy od głębokości wyszukiwania, z której korzystamy. Im większa głębokość wyszukiwania, tym większa dokładność i tym więcej czasu potrzeba na uruchomienie. W moich testach wyszukiwanie z głębokością 3 trwa krócej niż 0.05 sekundy, ale daje 20% szans na wygraną, głębokość 5 trwa około 1 sekundy, ale daje 40% szans na wygraną, a ostatecznie głębokość 7 trwa 27-28 sekund i daje około 70-80% szans na wygraną.

Przyszłe rozszerzenia

Dla tych z Was, którzy są zainteresowani ulepszeniem kodu, oto kilka rzeczy, którym mogą się przyjrzeć:

1. Popraw prędkość: Poprawa szybkości algorytmu pozwoli na użycie większej głębokości, a tym samym na lepszą dokładność.
2. Utwórz grafikę: Nie bez powodu realizacja Gabriele Cirulli stała się tak sławna. Ładnie wygląda! Nie zawracałem sobie głowy tworzeniem GUI, ale raczej wydrukowałem wyniki na konsoli, co utrudnia śledzenie i granie w grę. Stworzenie ładnego GUI jest koniecznością.
3. Dostrój heurystykę: Jak wspomniałem wcześniej, kilku użytkowników zasugerowało różne heurystyki. Można poeksperymentować ze sposobem obliczania wyników, wagami i cechami planszy, które są brane pod uwagę. Moje podejście do mierzenia wyniku klastra ma łączyć inne sugestie, takie jak Monotoniczność i Gładkość, ale wciąż jest miejsce na ulepszenia.
4. Dostrajanie głębi: Można też spróbować dostroić / dopasować głębokość wyszukiwania w zależności od stanu gry. Możesz również użyć Iteracyjne pogłębianie - pierwsze wyszukiwanie głębokości algorytm, o którym wiadomo, że usprawnia algorytm przycinania alfa-beta.

Nie zapomnij pobrać kodu JAVA z Github i eksperymentuj. Mam nadzieję, że podobał Ci się ten post! Jeśli tak, poświęć chwilę, aby udostępnić artykuł na Facebooku i Twitterze. 🙂