1NTT Communication Science Laboratories, NTT Corporation, 3-1 Morinosato Wakamiya, Atsugi, Kanagawa 243-0198, Japan
2Faculty of Informatics, Gunma University, 4-2 Aramakimachi, Maebashi, Gunma 371-8510, Japan
3Yukawa Institute for Theoretical Physics, Kyoto University, Kitashirakawa Oiwakecho, Sakyo-ku, Kyoto 606-8502, Japan
4International Research Frontiers Initiative (IRFI), Tokyo Institute of Technology, Japan
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
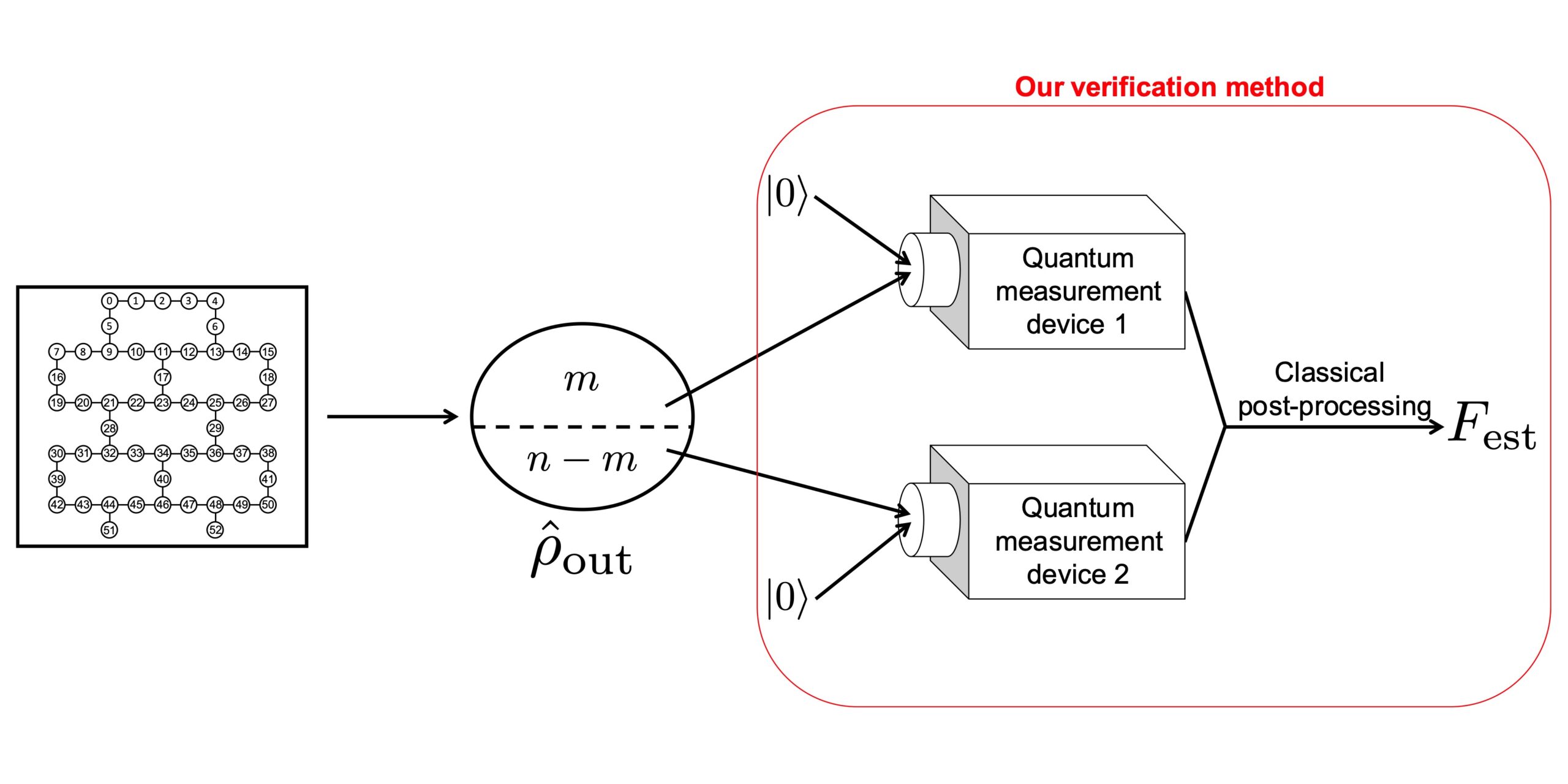
Several noisy intermediate-scale quantum computations can be regarded as logarithmic-depth quantum circuits on a sparse quantum computing chip, where two-qubit gates can be directly applied on only some pairs of qubits. In this paper, we propose a method to efficiently verify such noisy intermediate-scale quantum computation. To this end, we first characterize small-scale quantum operations with respect to the diamond norm. Then by using these characterized quantum operations, we estimate the fidelity $langlepsi_t|hat{rho}_{rm out}|psi_trangle$ between an actual $n$-qubit output state $hat{rho}_{rm out}$ obtained from the noisy intermediate-scale quantum computation and the ideal output state (i.e., the target state) $|psi_trangle$. Although the direct fidelity estimation method requires $O(2^n)$ copies of $hat{rho}_{rm out}$ on average, our method requires only $O(D^32^{12D})$ copies even in the worst case, where $D$ is the denseness of $|psi_trangle$. For logarithmic-depth quantum circuits on a sparse chip, $D$ is at most $O(log{n})$, and thus $O(D^32^{12D})$ is a polynomial in $n$. By using the IBM Manila 5-qubit chip, we also perform a proof-of-principle experiment to observe the practical performance of our method.
► BibTeX data
► References
[1] J. Preskill, Quantum Computing in the NISQ era and beyond, Quantum 2, 79 (2018).
https://doi.org/10.22331/q-2018-08-06-79
[2] A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. O’Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun. 5, 4213 (2014).
https://doi.org/10.1038/ncomms5213
[3] E. Farhi, J. Goldstone, and S. Gutmann, A Quantum Approximate Optimization Algorithm, arXiv:1411.4028.
https://doi.org/10.48550/arxiv.1411.4028
arXiv:1411.4028
[4] K. Mitarai, M. Negoro, M. Kitagawa, and K. Fujii, Quantum circuit learning, Phys. Rev. A 98, 032309 (2018).
https://doi.org/10.1103/PhysRevA.98.032309
[5] A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow, and J. M. Gambetta, Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets, Nature (London) 549, 242 (2017).
https://doi.org/10.1038/nature23879
[6] V. Havlíček, A. D. Córcoles, K. Temme, A. W. Harrow, A. Kandaka, J. M. Chow, and J. M. Gambetta, Supervised learning with quantum-enhanced feature spaces, Nature (London) 567, 209 (2019).
https://doi.org/10.1038/s41586-019-0980-2
[7] Y. Li and S. C. Benjamin, Efficient Variational Quantum Simulator Incorporating Active Error Minimization, Phys. Rev. X 7, 021050 (2017).
https://doi.org/10.1103/PhysRevX.7.021050
[8] K. Temme, S. Bravyi, and J. M. Gambetta, Error Mitigation for Short-Depth Quantum Circuits, Phys. Rev. Lett. 119, 180509 (2017).
https://doi.org/10.1103/PhysRevLett.119.180509
[9] S. Endo, S. C. Benjamin, and Y. Li, Practical Quantum Error Mitigation for Near-Future Applications, Phys. Rev. X 8, 031027 (2018).
https://doi.org/10.1103/PhysRevX.8.031027
[10] V. N. Premakumar and R. Joynt, Error Mitigation in Quantum Computers subject to Spatially Correlated Noise, arXiv:1812.07076.
https://doi.org/10.48550/arxiv.1812.07076
arXiv:1812.07076
[11] X. Bonet-Monroig, R. Sagastizabal, M. Singh, and T. E. O’Brien, Low-cost error mitigation by symmetry verification, Phys. Rev. A 98, 062339 (2018).
https://doi.org/10.1103/PhysRevA.98.062339
[12] J. Sun, X. Yuan, T. Tsunoda, V. Vedral, S. C. Benjamin, and S. Endo, Mitigating Realistic Noise in Practical Noisy Intermediate-Scale Quantum Devices, Phys. Rev. Applied 15, 034026 (2021).
https://doi.org/10.1103/PhysRevApplied.15.034026
[13] X.-M. Zhang, W. Kong, M. U. Farooq, M.-H. Yung, G. Guo, and X. Wang, Generic detection-based error mitigation using quantum autoencoders, Phys. Rev. A 103, L040403 (2021).
https://doi.org/10.1103/PhysRevA.103.L040403
[14] A. Strikis, D. Qin, Y. Chen, S. C. Benjamin, and Y. Li, Learning-Based Quantum Error Mitigation, PRX Quantum 2, 040330 (2021).
https://doi.org/10.1103/PRXQuantum.2.040330
[15] P. Czarnik, A. Arrasmith, P. J. Coles, and L. Cincio, Error mitigation with Clifford quantum-circuit data, Quantum 5, 592 (2021).
https://doi.org/10.22331/q-2021-11-26-592
[16] A. Zlokapa and A. Gheorghiu, A deep learning model for noise prediction on near-term quantum devices, arXiv:2005.10811.
https://doi.org/10.48550/arxiv.2005.10811
arXiv:2005.10811
[17] K. Yeter-Aydeniz, R. C. Pooser, and G. Siopsis, Practical quantum computation of chemical and nuclear energy levels using quantum imaginary time evolution and Lanczos algorithms, npj Quantum Information 6, 63 (2020).
https://doi.org/10.1038/s41534-020-00290-1
[18] B. Tan and J. Cong, Optimality Study of Existing Quantum Computing Layout Synthesis Tools, IEEE Transactions on Computers 70, 1363 (2021).
https://doi.org/10.1109/TC.2020.3009140
[19] M. R. Perelshtein, A. I. Pakhomchik, A. A. Melnikov, A. A. Novikov, A. Glatz, G. S. Paraoanu, V. M. Vinokur, and G. B. Lesovik, Solving Large-Scale Linear Systems of Equations by a Quantum Hybrid Algorithm, Ann. Phys. 2200082 (2022).
https://doi.org/10.1002/andp.202200082
[20] A. Kondratyev, Non-Differentiable Learning of Quantum Circuit Born Machine with Genetic Algorithm, Wilmott 2021, 50 (2021).
https://doi.org/10.1002/wilm.10943
[21] S. Dasgupta, K. E. Hamilton, and A. Banerjee, Characterizing the memory capacity of transmon qubit reservoirs, arXiv:2004.08240.
https://doi.org/10.48550/arxiv.2004.08240
arXiv:2004.08240
[22] L. M. Sager, S. E. Smart, D. A. Mazziotti, Preparation of an exciton condensate of photons on a 53-qubit quantum computer, Phys. Rev. Research 2, 043205 (2020).
https://doi.org/10.1103/PhysRevResearch.2.043205
[23] J. R. Wootton, A quantum procedure for map generation, in Proc. of the 2020 IEEE Conference on Games (IEEE, Osaka, 2020), p. 73.
https://doi.org/10.1109/CoG47356.2020.9231571
[24] W.-J. Huang, W.-C. Chien, C.-H. Cho, C.-C. Huang, T.-W. Huang, and C.-R. Chang, Mermin’s inequalities of multiple qubits with orthogonal measurements on IBM Q 53-qubit system, Quantum Engineering 2, e45 (2020).
https://doi.org/10.1002/que2.45
[25] T. Morimae, Verification for measurement-only blind quantum computing, Phys. Rev. A 89, 060302(R) (2014).
https://doi.org/10.1103/PhysRevA.89.060302
[26] M. Hayashi and T. Morimae, Verifiable Measurement-Only Blind Quantum Computing with Stabilizer Testing, Phys. Rev. Lett. 115, 220502 (2015).
https://doi.org/10.1103/PhysRevLett.115.220502
[27] T. Morimae, Measurement-only verifiable blind quantum computing with quantum input verification, Phys. Rev. A 94, 042301 (2016).
https://doi.org/10.1103/PhysRevA.94.042301
[28] D. Aharonov, M. Ben-Or, E. Eban, and U. Mahadev, Interactive Proofs for Quantum Computations, arXiv:1704.04487.
https://doi.org/10.48550/arxiv.1704.04487
arXiv:1704.04487
[29] J. F. Fitzsimons and E. Kashefi, Unconditionally verifiable blind quantum computation, Phys. Rev. A 96, 012303 (2017).
https://doi.org/10.1103/PhysRevA.96.012303
[30] T. Morimae, Y. Takeuchi, and M. Hayashi, Verification of hypergraph states, Phys. Rev. A 96, 062321 (2017).
https://doi.org/10.1103/PhysRevA.96.062321
[31] J. F. Fitzsimons, M. Hajdušek, and T. Morimae, Post hoc Verification of Quantum Computation, Phys. Rev. Lett. 120, 040501 (2018).
https://doi.org/10.1103/PhysRevLett.120.040501
[32] Y. Takeuchi and T. Morimae, Verification of Many-Qubit States, Phys. Rev. X 8, 021060 (2018).
https://doi.org/10.1103/PhysRevX.8.021060
[33] A. Broadbent, How to Verify a Quantum Computation, Theory of Computing 14, 11 (2018).
https://doi.org/10.4086/toc.2018.v014a011
[34] U. Mahadev, Classical Verification of Quantum Computations, in Proc. of the 59th Annual Symposium on Foundations of Computer Science (IEEE, Paris, 2018), p. 259.
https://doi.ieeecomputersociety.org/10.1109/FOCS.2018.00033
[35] Y. Takeuchi, A. Mantri, T. Morimae, A. Mizutani, and J. F. Fitzsimons, Resource-efficient verification of quantum computing using Serfling’s bound, npj Quantum Information 5, 27 (2019).
https://doi.org/10.1038/s41534-019-0142-2
[36] M. Hayashi and Y. Takeuchi, Verifying commuting quantum computations via fidelity estimation of weighted graph states, New J. Phys. 21, 093060 (2019).
https://doi.org/10.1088/1367-2630/ab3d88
[37] A. Gheorghiu and T. Vidick, Computationally-Secure and Composable Remote State Preparation, in Proc. of the 60th Annual Symposium on Foundations of Computer Science (IEEE, Baltimore, 2019), p. 1024.
https://doi.org/10.1109/FOCS.2019.00066
[38] G. Alagic, A. M. Childs, A. B. Grilo, and S.-H. Hung, Non-interactive Classical Verification of Quantum Computation, in Proc. of Theory of Cryptography Conference (Springer, Virtual, 2020), p. 153.
https://doi.org/10.1007/978-3-030-64381-2_6
[39] H. Zhu and M. Hayashi, Efficient Verification of Hypergraph States, Phys. Rev. Applied 12, 054047 (2019).
https://doi.org/10.1103/PhysRevApplied.12.054047
[40] N.-H. Chia, K.-M. Chung, and T. Yamakawa, Classical Verification of Quantum Computations with Efficient Verifier, in Proc. of Theory of Cryptography Conference (Springer, Virtual, 2020), p. 181.
https://doi.org/10.1007/978-3-030-64381-2_7
[41] D. Markham and A. Krause, A Simple Protocol for Certifying Graph States and Applications in Quantum Networks, Cryptography 4, 3 (2020).
https://doi.org/10.3390/cryptography4010003
[42] R. Raussendorf and H. J. Briegel, A One-Way Quantum Computer, Phys. Rev. Lett. 86, 5188 (2001).
https://doi.org/10.1103/PhysRevLett.86.5188
[43] O. Regev, On lattices, learning with errors, random linear codes, and cryptography, Journal of the ACM 56, 34 (2009).
https://doi.org/10.1145/1568318.1568324
[44] If $n$-qubit quantum operations are allowed, the efficient verification is trivially possible. Let $U$ be a unitary operator such that $|psi_trangle=U|0^nrangle$ for an ideal output state $|psi_trangle$. We apply $U^†$ to a received state $hat{rho}$ and measure all qubits in the computational basis. Then, by estimating the probability of $0^n$ being observed, we can estimate the fidelity $langle 0^n|U^†hat{rho}U|0^nrangle$ between $|psi_trangle$ and $hat{rho}$.
[45] For clarity, we use the notation $hat{a}$ when the lowercase letter $a$ is a quantum state or quantum operation. On the other hand, for any uppercase letter $A$, we omit $hat{color{white}{a}}$ even if $A$ is a quantum state or quantum operation.
[46] D. T. Smithey, M. Beck, M. G. Raymer, and A. Faridani, Measurement of the Wigner distribution and the density matrix of a light mode using optical homodyne tomography: Application to squeezed states and the vacuum, Phys. Rev. Lett. 70, 1244 (1993).
https://doi.org/10.1103/PhysRevLett.70.1244
[47] Z. Hradil, Quantum-state estimation, Phys. Rev. A 55, R1561(R) (1997).
https://doi.org/10.1103/PhysRevA.55.R1561
[48] K. Banaszek, G. M. D’Ariano, M. G. A. Paris, and M. F. Sacchi, Maximum-likelihood estimation of the density matrix, Phys. Rev. A 61, 010304(R) (1999).
https://doi.org/10.1103/PhysRevA.61.010304
[49] S. T. Flammia and Y.-K. Liu, Direct Fidelity Estimation from Few Pauli Measurements, Phys. Rev. Lett. 106, 230501 (2011).
https://doi.org/10.1103/PhysRevLett.106.230501
[50] S. Ferracin, T. Kapourniotis, and A. Datta, Accrediting outputs of noisy intermediate-scale quantum computing devices, New J. Phys. 21 113038 (2019).
https://doi.org/10.1088/1367-2630/ab4fd6
[51] S. Ferracin, S. T. Merkel, D. McKay, and A. Datta, Experimental accreditation of outputs of noisy quantum computers, Phys. Rev. A 104, 042603 (2021).
https://doi.org/10.1103/PhysRevA.104.042603
[52] D. Leichtle, L. Music, E. Kashefi, and H. Ollivier, Verifying BQP Computations on Noisy Devices with Minimal Overhead, PRX Quantum 2, 040302 (2021).
https://doi.org/10.1103/PRXQuantum.2.040302
[53] Y.-C. Liu, X.-D. Yu, J. Shang, H. Zhu, and X. Zhang, Efficient Verification of Dicke States, Phys. Rev. Applied 12, 044020 (2019).
https://doi.org/10.1103/PhysRevApplied.12.044020
[54] S. Bravyi, G. Smith, and J. A. Smolin, Trading Classical and Quantum Computational Resources, Phys. Rev. X 6, 021043 (2016).
https://doi.org/10.1103/PhysRevX.6.021043
[55] T. Peng, A. Harrow, M. Ozols, and X. Wu, Simulating Large Quantum Circuits on a Small Quantum Computer, Phys. Rev. Lett. 125, 150504 (2020).
https://doi.org/10.1103/PhysRevLett.125.150504
[56] D. Aharonov, A. Kitaev, and N. Nisan, Quantum Circuits with Mixed States, in Proc. of the 30th Annual ACM Symposium on Theory of Computing (ACM, Dallas, 1998), p. 20.
https://doi.org/10.1145/276698.276708
[57] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information 10th Anniversary Edition (Cambridge University Press, Cambridge, 2010).
https://doi.org/10.1017/CBO9780511976667
[58] M. Fanciulli, ed., Electron Spin Resonance and Related Phenomena in Low-Dimensional Structures (Springer, Berlin, 2009).
https://doi.org/10.1007/978-3-540-79365-6
[59] W. Hoeffding, Probability Inequalities for Sums of Bounded Random Variables, Journal of the American Statistical Association 58, 13 (1963).
https://www.tandfonline.com/doi/ref/10.1080/01621459.1963.10500830?scroll=top
[60] K. Li and G. Smith, Quantum de Finetti Theorem under Fully-One-Way Adaptive Measurements, Phys. Rev. Lett. 114, 160503 (2015).
https://doi.org/10.1103/PhysRevLett.114.160503
[61] F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Y. Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis, Quantum supremacy using a programmable superconducting processor, Nature (London) 574, 505 (2019).
https://doi.org/10.1038/s41586-019-1666-5
[62] R. J. Lipton and R. E. Tarjan, A Separator Theorem for Planar Graphs, SIAM J. Appl. Math. 36, 177 (1979).
https://doi.org/10.1137/0136016
[63] R. J. Lipton and R. E. Tarjan, Applications of a Planar Separator Theorem, SIAM J. Comput. 9, 615 (1980).
https://doi.org/10.1137/0209046
[64] K. Fujii, K. Mizuta, H. Ueda, K. Mitarai, W. Mizukami, Y. O. Nakagawa, Deep Variational Quantum Eigensolver: A Divide-And-Conquer Method for Solving a Larger Problem with Smaller Size Quantum Computers, PRX Quantum 3, 010346 (2022).
https://doi.org/10.1103/PRXQuantum.3.010346
[65] W. Tang, T. Tomesh, M. Suchara, J. Larson, and M. Martonosi, CutQC: using small Quantum computers for large Quantum circuit evaluations, in Proc. of the 26th ACM International Conference on Architectural Support for Programming Languages and Operating Systems (ACM, Virtual, 2021), p. 473.
https://doi.org/10.1145/3445814.3446758
[66] K. Mitarai and K. Fujii, Constructing a virtual two-qubit gate by sampling single-qubit operations, New J. Phys. 23, 023021 (2021).
https://doi.org/10.1088/1367-2630/abd7bc
[67] K. Mitarai and K. Fujii, Overhead for simulating a non-local channel with local channesl by quasiprobability sampling, Quantum 5, 388 (2021).
https://doi.org/10.22331/q-2021-01-28-388
[68] M. A. Perlin, Z. H. Saleem, M. Suchara, and J. C. Osborn, Quantum circuit cutting with maximum-likelihood tomography, npj Quantum Information 7, 64 (2021).
https://doi.org/10.1038/s41534-021-00390-6
[69] T. Ayral, F.-M. L Régent, Z. Saleem, Y. Alexeev, and M. Suchara, Quantum Divide and Compute: Hardware Demonstrations and Noisy Simulations, in Proc. of the 2020 IEEE Computer Society Annual Symposium on VLSI (IEEE, Limassol, 2020), p. 138.
https://doi.org/10.1109/ISVLSI49217.2020.00034
Cited by
[1] Ruge Lin and Weiqiang Wen, “Quantum computation capability verification protocol for noisy intermediate-scale quantum devices with the dihedral coset problem”, Physical Review A 106 1, 012430 (2022).
[2] Ruge Lin and Weiqiang Wen, “Quantum computation capability verification protocol for NISQ devices with dihedral coset problem”, arXiv:2202.06984.
The above citations are from Crossref’s cited-by service (last updated successfully 2022-07-27 01:37:47) and SAO/NASA ADS (last updated successfully 2022-07-27 01:37:48). The list may be incomplete as not all publishers provide suitable and complete citation data.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.