QSTAR, INO-CNR and LENS, Largo Enrico Fermi 2, 50125 Firenze, Italy
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
Discarding undesirable measurement results in Bell experiments opens the detection loophole that prevents a conclusive demonstration of nonlocality. As closing the detection loophole represents a major technical challenge for many practical Bell experiments, it is customary to assume the so-called fair sampling assumption (FSA) that, in its original form, states that the collectively postselected statistics are a fair sample of the ideal statistics. Here, we analyze the FSA from the viewpoint of causal inference: We derive a causal structure that must be present in any causal model that faithfully encapsulates the FSA. This provides an easy, intuitive, and unifying approach that includes different accepted forms of the FSA and underlines what is really assumed when using the FSA. We then show that the FSA can not only be applied in scenarios with non-ideal detectors or transmission losses, but also in ideal experiments where only parts of the correlations are postselected, e.g., when the particles’ destinations are in a superposition state. Finally, we demonstrate that the FSA is also applicable in multipartite scenarios that test for (genuine) multipartite nonlocality.
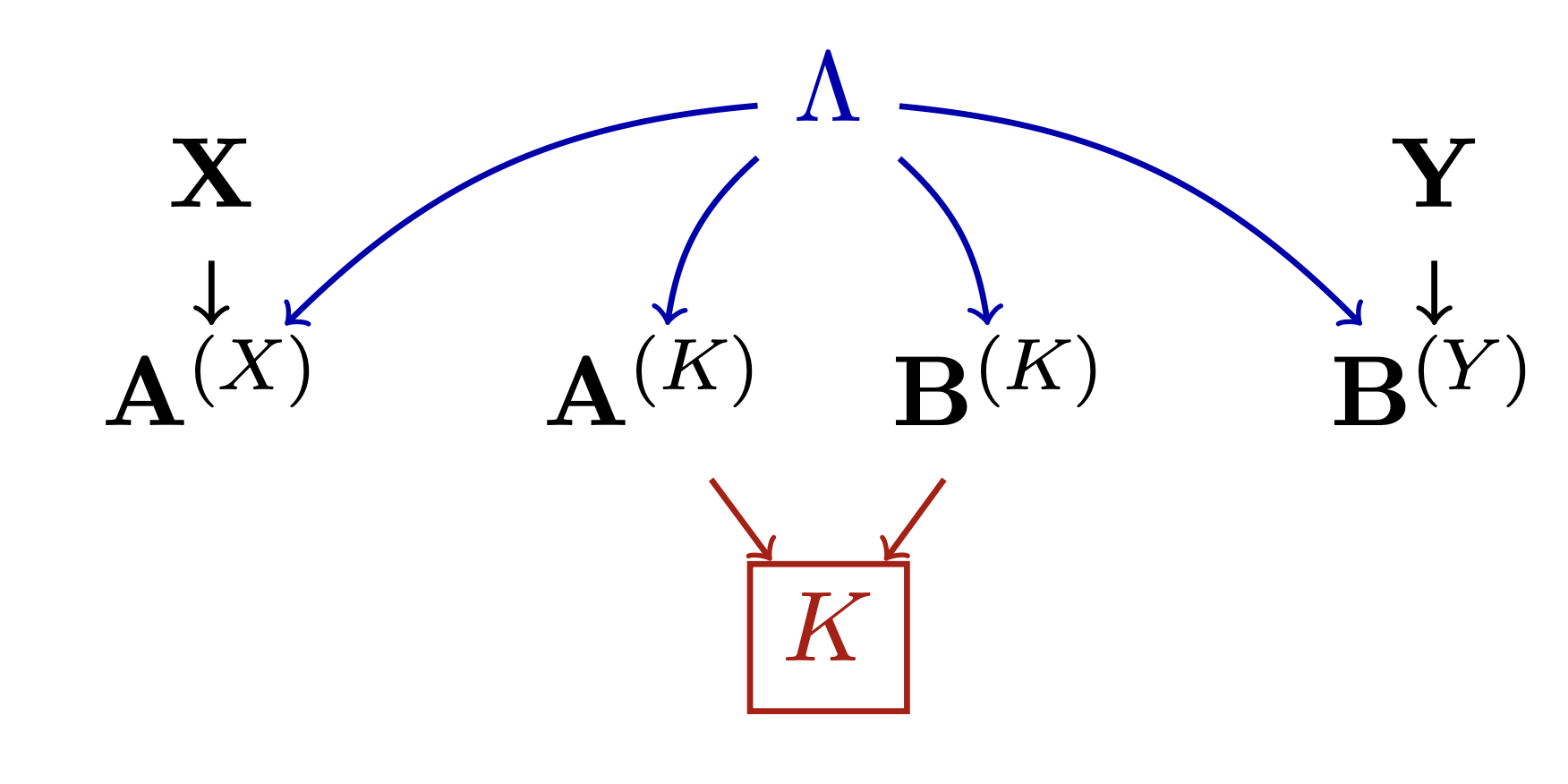
Featured image: Causal structure of a faithful explanation of the fair sampling assumption.
Popular summary
► BibTeX data
► References
[1] John S Bell. “On the einstein podolsky rosen paradox”. Physics 1, 195 (1964).
https://doi.org/10.1103/PhysicsPhysiqueFizika.1.195
[2] John S Bell. “The theory of local beables”. In Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy. Pages 52–62. Cambridge University Press (2004). 2 edition.
https://doi.org/10.1017/CBO9780511815676
[3] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner. “Bell nonlocality”. Rev. Mod. Phys. 86, 419–478 (2014).
https://doi.org/10.1103/RevModPhys.86.419
[4] Judea Pearl. “Causality: Models, reasoning, and inference”. Cambridge University Press. (2009).
https://doi.org/10.1017/CBO9780511803161
[5] Philip M. Pearle. “Hidden-variable example based upon data rejection”. Phys. Rev. D 2, 1418–1425 (1970).
https://doi.org/10.1103/PhysRevD.2.1418
[6] John F. Clauser and Michael A. Horne. “Experimental consequences of objective local theories”. Phys. Rev. D 10, 526–535 (1974).
https://doi.org/10.1103/PhysRevD.10.526
[7] D. S. Tasca, S. P. Walborn, F. Toscano, and P. H. Souto Ribeiro. “Observation of tunable popescu-rohrlich correlations through postselection of a gaussian state”. Phys. Rev. A 80, 030101 (2009).
https://doi.org/10.1103/PhysRevA.80.030101
[8] Ilja Gerhardt, Qin Liu, Antía Lamas-Linares, Johannes Skaar, Valerio Scarani, Vadim Makarov, and Christian Kurtsiefer. “Experimentally faking the violation of bell’s inequalities”. Phys. Rev. Lett. 107, 170404 (2011).
https://doi.org/10.1103/PhysRevLett.107.170404
[9] Enrico Pomarico, Bruno Sanguinetti, Pavel Sekatski, Hugo Zbinden, and Nicolas Gisin. “Experimental amplification of an entangled photon: what if the detection loophole is ignored?”. New J. Phys. 13, 063031 (2011).
https://doi.org/10.1088/1367-2630/13/6/063031
[10] J Romero, D Giovannini, D S Tasca, S M Barnett, and M J Padgett. “Tailored two-photon correlation and fair-sampling: a cautionary tale”. New J. Phys. 15, 083047 (2013).
https://doi.org/10.1088/1367-2630/15/8/083047
[11] N. David Mermin. “The EPR experiment—thoughts about the “loophole””. Ann. N. Y. Acad. Sci. 480, 422–427 (1986).
https://doi.org/10.1111/j.1749-6632.1986.tb12444.x
[12] Philippe H. Eberhard. “Background level and counter efficiencies required for a loophole-free einstein-podolsky-rosen experiment”. Phys. Rev. A 47, R747–R750 (1993).
https://doi.org/10.1103/PhysRevA.47.R747
[13] Fabio Sciarrino, Giuseppe Vallone, Adán Cabello, and Paolo Mataloni. “Bell experiments with random destination sources”. Phys. Rev. A 83, 032112 (2011).
https://doi.org/10.1103/PhysRevA.83.032112
[14] Anupam Garg and N. D. Mermin. “Detector inefficiencies in the einstein-podolsky-rosen experiment”. Phys. Rev. D 35, 3831–3835 (1987).
https://doi.org/10.1103/PhysRevD.35.3831
[15] Jan-Åke Larsson. “Bell’s inequality and detector inefficiency”. Phys. Rev. A 57, 3304–3308 (1998).
https://doi.org/10.1103/PhysRevA.57.3304
[16] Mary A Rowe, David Kielpinski, Volker Meyer, Charles A Sackett, Wayne M Itano, Christopher Monroe, and David J Wineland. “Experimental violation of a bell’s inequality with efficient detection”. Nature 409, 791–794 (2001).
https://doi.org/10.1038/35057215
[17] D. N. Matsukevich, P. Maunz, D. L. Moehring, S. Olmschenk, and C. Monroe. “Bell inequality violation with two remote atomic qubits”. Phys. Rev. Lett. 100, 150404 (2008).
https://doi.org/10.1103/PhysRevLett.100.150404
[18] B. G. Christensen, K. T. McCusker, J. B. Altepeter, B. Calkins, T. Gerrits, A. E. Lita, A. Miller, L. K. Shalm, Y. Zhang, S. W. Nam, N. Brunner, C. C. W. Lim, N. Gisin, and P. G. Kwiat. “Detection-loophole-free test of quantum nonlocality, and applications”. Phys. Rev. Lett. 111, 130406 (2013).
https://doi.org/10.1103/PhysRevLett.111.130406
[19] Lynden K. Shalm, Evan Meyer-Scott, Bradley G. Christensen, Peter Bierhorst, Michael A. Wayne, Martin J. Stevens, Thomas Gerrits, Scott Glancy, Deny R. Hamel, Michael S. Allman, Kevin J. Coakley, Shellee D. Dyer, Carson Hodge, Adriana E. Lita, Varun B. Verma, Camilla Lambrocco, Edward Tortorici, Alan L. Migdall, Yanbao Zhang, Daniel R. Kumor, William H. Farr, Francesco Marsili, Matthew D. Shaw, Jeffrey A. Stern, Carlos Abellán, Waldimar Amaya, Valerio Pruneri, Thomas Jennewein, Morgan W. Mitchell, Paul G. Kwiat, Joshua C. Bienfang, Richard P. Mirin, Emanuel Knill, and Sae Woo Nam. “Strong loophole-free test of local realism”. Phys. Rev. Lett. 115, 250402 (2015).
https://doi.org/10.1103/PhysRevLett.115.250402
[20] Marissa Giustina, Marijn A. M. Versteegh, Sören Wengerowsky, Johannes Handsteiner, Armin Hochrainer, Kevin Phelan, Fabian Steinlechner, Johannes Kofler, Jan-Åke Larsson, Carlos Abellán, Waldimar Amaya, Valerio Pruneri, Morgan W. Mitchell, Jörn Beyer, Thomas Gerrits, Adriana E. Lita, Lynden K. Shalm, Sae Woo Nam, Thomas Scheidl, Rupert Ursin, Bernhard Wittmann, and Anton Zeilinger. “Significant-loophole-free test of bell’s theorem with entangled photons”. Phys. Rev. Lett. 115, 250401 (2015).
https://doi.org/10.1103/PhysRevLett.115.250401
[21] Bas Hensen, Hannes Bernien, Anaïs E Dréau, Andreas Reiserer, Norbert Kalb, Machiel S Blok, Just Ruitenberg, Raymond FL Vermeulen, Raymond N Schouten, Carlos Abellán, et al. “Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres”. Nature 526, 682–686 (2015).
https://doi.org/10.1038/nature15759
[22] John F. Clauser, Michael A. Horne, Abner Shimony, and Richard A. Holt. “Proposed experiment to test local hidden-variable theories”. Phys. Rev. Lett. 23, 880–884 (1969).
https://doi.org/10.1103/PhysRevLett.23.880
[23] Dominic W. Berry, Hyunseok Jeong, Magdalena Stobińska, and Timothy C. Ralph. “Fair-sampling assumption is not necessary for testing local realism”. Phys. Rev. A 81, 012109 (2010).
https://doi.org/10.1103/PhysRevA.81.012109
[24] Davide Orsucci, Jean-Daniel Bancal, Nicolas Sangouard, and Pavel Sekatski. “How post-selection affects device-independent claims under the fair sampling assumption”. Quantum 4, 238 (2020).
https://doi.org/10.22331/q-2020-03-02-238
[25] Igor Marinković, Andreas Wallucks, Ralf Riedinger, Sungkun Hong, Markus Aspelmeyer, and Simon Gröblacher. “Optomechanical bell test”. Phys. Rev. Lett. 121, 220404 (2018).
https://doi.org/10.1103/PhysRevLett.121.220404
[26] Dominik Rauch, Johannes Handsteiner, Armin Hochrainer, Jason Gallicchio, Andrew S. Friedman, Calvin Leung, Bo Liu, Lukas Bulla, Sebastian Ecker, Fabian Steinlechner, Rupert Ursin, Beili Hu, David Leon, Chris Benn, Adriano Ghedina, Massimo Cecconi, Alan H. Guth, David I. Kaiser, Thomas Scheidl, and Anton Zeilinger. “Cosmic bell test using random measurement settings from high-redshift quasars”. Phys. Rev. Lett. 121, 080403 (2018).
https://doi.org/10.1103/PhysRevLett.121.080403
[27] Emanuele Polino, Iris Agresti, Davide Poderini, Gonzalo Carvacho, Giorgio Milani, Gabriela Barreto Lemos, Rafael Chaves, and Fabio Sciarrino. “Device-independent test of a delayed choice experiment”. Phys. Rev. A 100, 022111 (2019).
https://doi.org/10.1103/PhysRevA.100.022111
[28] S. Gómez, A. Mattar, I. Machuca, E. S. Gómez, D. Cavalcanti, O. Jiménez Farías, A. Acín, and G. Lima. “Experimental investigation of partially entangled states for device-independent randomness generation and self-testing protocols”. Phys. Rev. A 99, 032108 (2019).
https://doi.org/10.1103/PhysRevA.99.032108
[29] Davide Poderini, Iris Agresti, Guglielmo Marchese, Emanuele Polino, Taira Giordani, Alessia Suprano, Mauro Valeri, Giorgio Milani, Nicolò Spagnolo, Gonzalo Carvacho, et al. “Experimental violation of n-locality in a star quantum network”. Nat. Commun. 11, 1–8 (2020).
https://doi.org/10.1038/s41467-020-16189-6
[30] Santiago Tarrago Velez, Vivishek Sudhir, Nicolas Sangouard, and Christophe Galland. “Bell correlations between light and vibration at ambient conditions”. Sci. Adv. 6, eabb0260 (2020).
https://doi.org/10.1126/sciadv.abb0260
[31] Iris Agresti, Davide Poderini, Leonardo Guerini, Michele Mancusi, Gonzalo Carvacho, Leandro Aolita, Daniel Cavalcanti, Rafael Chaves, and Fabio Sciarrino. “Experimental device-independent certified randomness generation with an instrumental causal structure”. Commun. Phys. 3, 1–7 (2020).
https://doi.org/10.1038/s42005-020-0375-6
[32] Peter Spirtes, Clark N Glymour, Richard Scheines, and David Heckerman. “Causation, prediction, and search”. MIT press. (2000).
https://doi.org/10.1017/CBO9780511803161
[33] Christopher J Wood and Robert W Spekkens. “The lesson of causal discovery algorithms for quantum correlations: causal explanations of bell-inequality violations require fine-tuning”. New J. Phys. 17, 033002 (2015).
https://doi.org/10.1088/1367-2630/17/3/033002
[34] John-Mark A. Allen, Jonathan Barrett, Dominic C. Horsman, Ciarán M. Lee, and Robert W. Spekkens. “Quantum common causes and quantum causal models”. Phys. Rev. X 7, 031021 (2017).
https://doi.org/10.1103/PhysRevX.7.031021
[35] Eric G. Cavalcanti. “Classical causal models for bell and kochen-specker inequality violations require fine-tuning”. Phys. Rev. X 8, 021018 (2018).
https://doi.org/10.1103/PhysRevX.8.021018
[36] Pawel Blasiak, Ewa Borsuk, and Marcin Markiewicz. “On safe post-selection for Bell tests with ideal detectors: Causal diagram approach”. Quantum 5, 575 (2021).
https://doi.org/10.22331/q-2021-11-11-575
[37] Valentin Gebhart, Luca Pezzè, and Augusto Smerzi. “Genuine multipartite nonlocality with causal-diagram postselection”. Phys. Rev. Lett. 127, 140401 (2021).
https://doi.org/10.1103/PhysRevLett.127.140401
[38] Valentin Gebhart and Augusto Smerzi. “Coincidence postselection for genuine multipartite nonlocality: Causal diagrams and threshold efficiencies” (2022). Phys. Rev. A 106, 062202 (2022).
https://doi.org/10.1103/PhysRevA.106.062202
[39] Bernard Yurke and David Stoler. “Bell’s-inequality experiments using independent-particle sources”. Phys. Rev. A 46, 2229–2234 (1992).
https://doi.org/10.1103/PhysRevA.46.2229
[40] Bernard Yurke and David Stoler. “Einstein-podolsky-rosen effects from independent particle sources”. Phys. Rev. Lett. 68, 1251–1254 (1992).
https://doi.org/10.1103/PhysRevLett.68.1251
[41] J. D. Franson. “Bell inequality for position and time”. Phys. Rev. Lett. 62, 2205–2208 (1989).
https://doi.org/10.1103/PhysRevLett.62.2205
[42] Sven Aerts, Paul Kwiat, Jan-Åke Larsson, and Marek Żukowski. “Two-photon franson-type experiments and local realism”. Phys. Rev. Lett. 83, 2872–2875 (1999).
https://doi.org/10.1103/PhysRevLett.83.2872
[43] Jonathan Jogenfors, Ashraf Mohamed Elhassan, Johan Ahrens, Mohamed Bourennane, and Jan Åke Larsson. “Hacking the bell test using classical light in energy-time entanglement–based quantum key distribution”. Sci. Adv. 1, e1500793 (2015).
https://doi.org/10.1126/sciadv.1500793
[44] Adán Cabello, Alessandro Rossi, Giuseppe Vallone, Francesco De Martini, and Paolo Mataloni. “Proposed bell experiment with genuine energy-time entanglement”. Phys. Rev. Lett. 102, 040401 (2009).
https://doi.org/10.1103/PhysRevLett.102.040401
[45] G. Lima, G. Vallone, A. Chiuri, A. Cabello, and P. Mataloni. “Experimental bell-inequality violation without the postselection loophole”. Phys. Rev. A 81, 040101 (2010).
https://doi.org/10.1103/PhysRevA.81.040101
[46] George Svetlichny. “Distinguishing three-body from two-body nonseparability by a bell-type inequality”. Phys. Rev. D 35, 3066–3069 (1987).
https://doi.org/10.1103/PhysRevD.35.3066
[47] N. David Mermin. “Extreme quantum entanglement in a superposition of macroscopically distinct states”. Phys. Rev. Lett. 65, 1838–1840 (1990).
https://doi.org/10.1103/PhysRevLett.65.1838
[48] Jean-Daniel Bancal, Cyril Branciard, Nicolas Gisin, and Stefano Pironio. “Quantifying multipartite nonlocality”. Phys. Rev. Lett. 103, 090503 (2009).
https://doi.org/10.1103/PhysRevLett.103.090503
[49] Jean-Daniel Bancal, Jonathan Barrett, Nicolas Gisin, and Stefano Pironio. “Definitions of multipartite nonlocality”. Phys. Rev. A 88, 014102 (2013).
https://doi.org/10.1103/PhysRevA.88.014102
[50] Patricia Contreras-Tejada, Carlos Palazuelos, and Julio I. de Vicente. “Genuine multipartite nonlocality is intrinsic to quantum networks”. Phys. Rev. Lett. 126, 040501 (2021).
https://doi.org/10.1103/PhysRevLett.126.040501
[51] Miguel Navascués, Elie Wolfe, Denis Rosset, and Alejandro Pozas-Kerstjens. “Genuine network multipartite entanglement”. Phys. Rev. Lett. 125, 240505 (2020).
https://doi.org/10.1103/PhysRevLett.125.240505
[52] Debashis Saha and Marcin Pawłowski. “Structure of quantum and broadcasting nonlocal correlations”. Phys. Rev. A 92, 062129 (2015).
https://doi.org/10.1103/PhysRevA.92.062129
[53] David Schmid, Thomas C. Fraser, Ravi Kunjwal, Ana Belen Sainz, Elie Wolfe, and Robert W. Spekkens. “Understanding the interplay of entanglement and nonlocality: motivating and developing a new branch of entanglement theory” (2021). arXiv:2004.09194.
https://doi.org/10.48550/arxiv.2004.09194
arXiv:2004.09194
[54] Xavier Coiteux-Roy, Elie Wolfe, and Marc-Olivier Renou. “No bipartite-nonlocal causal theory can explain nature’s correlations”. Phys. Rev. Lett. 127, 200401 (2021).
https://doi.org/10.1103/PhysRevLett.127.200401
[55] Rafael Chaves, Daniel Cavalcanti, and Leandro Aolita. “Causal hierarchy of multipartite Bell nonlocality”. Quantum 1, 23 (2017).
https://doi.org/10.22331/q-2017-08-04-23
Cited by
[1] Valentin Gebhart and Augusto Smerzi, “Coincidence postselection for genuine multipartite nonlocality: Causal diagrams and threshold efficiencies”, Physical Review A 106 6, 062202 (2022).
The above citations are from SAO/NASA ADS (last updated successfully 2023-01-13 11:42:16). The list may be incomplete as not all publishers provide suitable and complete citation data.
Could not fetch Crossref cited-by data during last attempt 2023-01-13 11:42:15: Could not fetch cited-by data for 10.22331/q-2023-01-13-897 from Crossref. This is normal if the DOI was registered recently.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.
- SEO Powered Content & PR Distribution. Get Amplified Today.
- Platoblockchain. Web3 Metaverse Intelligence. Knowledge Amplified. Access Here.
- Source: https://quantum-journal.org/papers/q-2023-01-13-897/
- 1
- 1.3
- 10
- 100
- 11
- 1998
- 1999
- 2001
- 2011
- 2014
- 2017
- 2018
- 2019
- 2020
- 2021
- 2022
- 28
- 39
- 7
- 9
- a
- About
- above
- ABSTRACT
- access
- affiliations
- algorithms
- All
- Ambient
- Ambient Conditions
- Ana
- analyze
- and
- applicable
- applications
- applied
- approach
- assumed
- assumption
- author
- authors
- avoided
- based
- Bell
- Bell Experiment
- between
- BLOK
- Branch
- Break
- Broadcasting
- Bruno
- Calvin
- cambridge
- causes
- Certified
- challenge
- challenging
- Charles
- choice
- Christensen
- Christopher
- claims
- closing
- coincidence
- collectively
- comment
- Common
- commonly
- Commons
- compare
- complete
- conditions
- Consequences
- copyright
- Correlation
- could
- Counter
- Daniel
- data
- David
- Delayed
- demonstrate
- destination
- destinations
- Detection
- developing
- diagrams
- different
- different forms
- Difficulty
- discovery
- discuss
- distinct
- distribution
- during
- edition
- Edward
- effects
- efficiencies
- efficient
- example
- experiment
- Explain
- explanation
- extending
- fair
- Finally
- form
- forms
- found
- from
- FSA
- generation
- George
- harvard
- here
- hierarchy
- highlights
- highly
- Hodge
- holders
- Hong
- HTTPS
- hugo
- ideal
- image
- in
- includes
- independent
- inequalities
- institutions
- instrumental
- interesting
- International
- intrinsic
- intuitive
- investigation
- IT
- Jan
- JavaScript
- John
- journal
- Key
- known
- Last
- Leave
- Lee
- lesson
- Level
- License
- light
- List
- literature
- local
- losses
- Main
- major
- many
- Martin
- max-width
- mechanics
- Meyer
- Michael
- Miller
- MIT
- model
- models
- Month
- Morgan
- Nam
- Nature
- necessary
- network
- networks
- New
- Nicolas
- normal
- objective
- obstacles
- ONE
- open
- opens
- original
- Paolo
- Paper
- papers
- Paradox
- parts
- Paul
- Peter
- Philippe
- philosophy
- Photons
- Physics
- plato
- Plato Data Intelligence
- PlatoData
- position
- possible
- Practical
- prediction
- present
- press
- protocols
- provide
- provides
- published
- publisher
- publishers
- Quantum
- quantum entanglement
- Quantum Mechanics
- quantum networks
- qubits
- Rafael
- Ralf
- random
- randomness
- recently
- references
- registered
- remains
- remote
- represents
- require
- required
- requirement
- restricted
- Results
- review
- Richard
- ROBERT
- safe
- scenarios
- SCI
- Search
- settings
- show
- Simon
- Sources
- spins
- Star
- State
- States
- statistics
- STEPHANIE
- structure
- Successfully
- such
- suitable
- superposition
- Technical
- test
- Testing
- tests
- The
- their
- threshold
- Through
- time
- Title
- to
- under
- university
- updated
- URL
- VIOLATION
- Violations
- volume
- W
- What
- What is
- which
- without
- Woo
- Work
- X
- year
- zephyrnet