Provably Accurate Simulation Of Gauge Theories And Bosonic Systems

Republished By Plato

Followers: 0

Yu Tong^1,2, Victor V. Albert³, Jarrod R. McClean¹, John Preskill^4,5, and Yuan Su^1,4

¹Google Quantum AI, Venice, CA, USA
²Department of Mathematics, University of California, Berkeley, CA, USA
³Joint Center for Quantum Information and Computer Science, NIST and University of Maryland, College Park, MD, USA
⁴Institute for Quantum Information and Matter, Caltech, Pasadena, CA, USA
⁵AWS Center for Quantum Computing, Pasadena, CA, USA

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

Quantum many-body systems involving bosonic modes or gauge fields have infinite-dimensional local Hilbert spaces which must be truncated to perform simulations of real-time dynamics on classical or quantum computers. To analyze the truncation error, we develop methods for bounding the rate of growth of local quantum numbers such as the occupation number of a mode at a lattice site, or the electric field at a lattice link. Our approach applies to various models of bosons interacting with spins or fermions, and also to both abelian and non-abelian gauge theories. We show that if states in these models are truncated by imposing an upper limit $Lambda$ on each local quantum number, and if the initial state has low local quantum numbers, then an error at most $epsilon$ can be achieved by choosing $Lambda$ to scale polylogarithmically with $epsilon^{-1}$, an exponential improvement over previous bounds based on energy conservation. For the Hubbard-Holstein model, we numerically compute a bound on $Lambda$ that achieves accuracy $epsilon$, obtaining significantly improved estimates in various parameter regimes. We also establish a criterion for truncating the Hamiltonian with a provable guarantee on the accuracy of time evolution. Building on that result, we formulate quantum algorithms for dynamical simulation of lattice gauge theories and of models with bosonic modes; the gate complexity depends almost linearly on spacetime volume in the former case, and almost quadratically on time in the latter case. We establish a lower bound showing that there are systems involving bosons for which this quadratic scaling with time cannot be improved. By applying our result on the truncation error in time evolution, we also prove that spectrally isolated energy eigenstates can be approximated with accuracy $epsilon$ by truncating local quantum numbers at $Lambda=textrm{polylog}(epsilon^{-1})$.

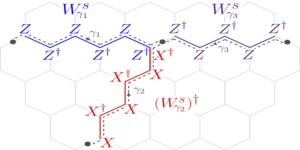
Featured image: A lattice with U(1) gauge field

[embedded content]

► BibTeX data

@article{Tong2022provablyaccurate, doi = {10.22331/q-2022-09-22-816}, url = {https://doi.org/10.22331/q-2022-09-22-816}, title = {Provably accurate simulation of gauge theories and bosonic systems}, author = {Tong, Yu and Albert, Victor V. and McClean, Jarrod R. and Preskill, John and Su, Yuan}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {6}, pages = {816}, month = sep, year = {2022} }

► References

[1] I. Arad, A. Kitaev, Z. Landau, and U. Vazirani. An area law and sub-exponential algorithm for 1D systems. arXiv preprint arXiv:1301.1162, 2013. 10.48550/arXiv.1301.1162.
https://doi.org/10.48550/arXiv.1301.1162
arXiv:1301.1162

[2] I. Arad, T. Kuwahara, and Z. Landau. Connecting global and local energy distributions in quantum spin models on a lattice. Journal of Statistical Mechanics: Theory and Experiment, 2016 (3): 033301, 2016. 10.1088/1742-5468/2016/03/033301.
https://doi.org/10.1088/1742-5468/2016/03/033301

[3] Y. Atia and D. Aharonov. Fast-forwarding of Hamiltonians and exponentially precise measurements. Nature Communications, 8 (1): 1572, Nov 2017. 10.1038/s41467-017-01637-7.
https://doi.org/10.1038/s41467-017-01637-7

[4] D. Banerjee, M. Dalmonte, M. Müller, E. Rico, P. Stebler, U.-J. Wiese, and P. Zoller. Atomic quantum simulation of dynamical gauge fields coupled to fermionic matter: From string breaking to evolution after a quench. Physical Review Letters, 109 (17): 175302, 2012. 10.1103/PhysRevLett.109.175302.
https://doi.org/10.1103/PhysRevLett.109.175302

[5] M. C. Bañuls, K. Cichy, J. I. Cirac, K. Jansen, and S. Kühn. Efficient basis formulation for $(1+1)$-dimensional SU(2) lattice gauge theory: Spectral calculations with matrix product states. Physical Review X, 7 (4): 041046, 2017. 10.1103/PhysRevX.7.041046.
https://doi.org/10.1103/PhysRevX.7.041046

[6] M. C. Banuls, R. Blatt, J. Catani, A. Celi, J. I. Cirac, M. Dalmonte, L. Fallani, K. Jansen, M. Lewenstein, S. Montangero, et al. Simulating lattice gauge theories within quantum technologies. The European physical journal D, 74 (8): 1–42, 2020. 10.1140/epjd/e2020-100571-8.
https://doi.org/10.1140/epjd/e2020-100571-8

[7] J. Bender, E. Zohar, A. Farace, and J. I. Cirac. Digital quantum simulation of lattice gauge theories in three spatial dimensions. New Journal of Physics, 20 (9): 093001, 2018. 10.1088/1367-2630/aadb71.
https://doi.org/10.1088/1367-2630/aadb71

[8] D. W. Berry and A. M. Childs. Black-box hamiltonian simulation and unitary implementation. Quantum Information & Computation, 12 (1-2): 29–62, 2012. 10.26421/QIC12.1-2.
https://doi.org/10.26421/QIC12.1-2

[9] D. W. Berry, G. Ahokas, R. Cleve, and B. C. Sanders. Efficient quantum algorithms for simulating sparse Hamiltonians. Communications in Mathematical Physics, 270 (2): 359–371, 2006. 10.1007/s00220-006-0150-x.
https://doi.org/10.1007/s00220-006-0150-x

[10] D. W. Berry, A. M. Childs, R. Cleve, R. Kothari, and R. D. Somma. Exponential improvement in precision for simulating sparse Hamiltonians. In Proceedings of the forty-sixth annual ACM symposium on Theory of computing, pages 283–292, 2014. 10.1145/2591796.2591854.
https://doi.org/10.1145/2591796.2591854

[11] D. W. Berry, A. M. Childs, and R. Kothari. Hamiltonian simulation with nearly optimal dependence on all parameters. In 2015 IEEE 56th Annual Symposium on Foundations of Computer Science, pages 792–809, 2015. 10.1145/3313276.3316386.
https://doi.org/10.1145/3313276.3316386

[12] X. Bonet-Monroig, R. Sagastizabal, M. Singh, and T. O’Brien. Low-cost error mitigation by symmetry verification. Physical Review A, 98 (6): 062339, 2018. 10.1103/PhysRevA.98.062339.
https://doi.org/10.1103/PhysRevA.98.062339

[13] T. Byrnes and Y. Yamamoto. Simulating lattice gauge theories on a quantum computer. Physical Review A, 73 (2): 022328, 2006. 10.1103/PhysRevA.73.022328.
https://doi.org/10.1103/PhysRevA.73.022328

[14] C. Canonne. A short note on Poisson tail bounds. 2017. URL http://www.cs.columbia.edu/ ccanonne/files/misc/2017-poissonconcentration.pdf.
http://www.cs.columbia.edu/~ccanonne/files/misc/2017-poissonconcentration.pdf

[15] B. Chakraborty, M. Honda, T. Izubuchi, Y. Kikuchi, and A. Tomiya. Classically emulated digital quantum simulation of the schwinger model with a topological term via adiabatic state preparation. Phys. Rev. D, 105: 094503, May 2022. 10.1103/PhysRevD.105.094503. URL https://link.aps.org/doi/10.1103/PhysRevD.105.094503.
https://doi.org/10.1103/PhysRevD.105.094503

[16] S.-H. Chang, P. C. Cosman, and L. B. Milstein. Chernoff-type bounds for the Gaussian error function. IEEE Transactions on Communications, 59 (11): 2939–2944, 2011. 10.1109/TCOMM.2011.072011.100049.
https://doi.org/10.1109/TCOMM.2011.072011.100049

[17] A. M. Childs and Y. Su. Nearly optimal lattice simulation by product formulas. Physical Review Letters, 123 (5): 050503, 2019. 10.1103/PhysRevLett.123.050503.
https://doi.org/10.1103/PhysRevLett.123.050503

[18] A. M. Childs, R. Kothari, and R. D. Somma. Quantum algorithm for systems of linear equations with exponentially improved dependence on precision. SIAM J. Comput., 46 (6): 1920–1950, 2017. 10.1137/16m1087072.
https://doi.org/10.1137/16m1087072

[19] A. M. Childs, Y. Su, M. C. Tran, N. Wiebe, and S. Zhu. Theory of Trotter error with commutator scaling. Physical Review X, 11 (1): 011020, 2021. 10.1103/PhysRevX.11.011020.
https://doi.org/10.1103/PhysRevX.11.011020

[20] Z. Davoudi, N. M. Linke, and G. Pagano. Toward simulating quantum field theories with controlled phonon-ion dynamics: A hybrid analog-digital approach. Phys. Rev. Research, 3: 043072, Oct 2021. 10.1103/PhysRevResearch.3.043072. URL https://link.aps.org/doi/10.1103/PhysRevResearch.3.043072.
https://doi.org/10.1103/PhysRevResearch.3.043072

[21] J. Del Pino, F. A. Schröder, A. W. Chin, J. Feist, and F. J. Garcia-Vidal. Tensor network simulation of non-Markovian dynamics in organic polaritons. Physical Review Letters, 121 (22): 227401, 2018. 10.1103/PhysRevLett.121.227401.
https://doi.org/10.1103/PhysRevLett.121.227401

[22] R. H. Dicke. Coherence in spontaneous radiation processes. Physical Review, 93 (1): 99, 1954. 10.1103/PhysRev.93.99.
https://doi.org/10.1103/PhysRev.93.99

[23] H. Fröhlich. Electrons in lattice fields. Advances in Physics, 3 (11): 325–361, 1954. 10.1080/00018735400101213.
https://doi.org/10.1080/00018735400101213

[24] A. Gilyén, Y. Su, G. H. Low, and N. Wiebe. Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, pages 193–204, 2019. 10.1145/3313276.3316366.
https://doi.org/10.1145/3313276.3316366

[25] F. Giustino. Electron-phonon interactions from first principles. Reviews of Modern Physics, 89 (1): 015003, 2017. 10.1103/RevModPhys.89.015003.
https://doi.org/10.1103/RevModPhys.89.015003

[26] S. Gu, R. D. Somma, and B. Şahinoğlu. Fast-forwarding quantum evolution. Quantum, 5: 577, 2021. 10.22331/q-2021-11-15-577.
https://doi.org/10.22331/q-2021-11-15-577

[27] C. Guo, A. Weichselbaum, J. von Delft, and M. Vojta. Critical and strong-coupling phases in one-and two-bath spin-boson models. Physical Review Letters, 108 (16): 160401, 2012. 10.1103/PhysRevLett.108.160401.
https://doi.org/10.1103/PhysRevLett.108.160401

[28] J. Haah, M. B. Hastings, R. Kothari, and G. H. Low. Quantum algorithm for simulating real time evolution of lattice Hamiltonians. SIAM Journal on Computing, (0): FOCS18–250, 2021. 10.1137/18M1231511.
https://doi.org/10.1137/18M1231511

[29] M. B. Hastings. Locality in quantum and Markov dynamics on lattices and networks. Physical Review Letters, 93 (14): 140402, 2004. 10.1103/PhysRevLett.93.140402.
https://doi.org/10.1103/PhysRevLett.93.140402

[30] M. B. Hastings. An area law for one-dimensional quantum systems. Journal of Statistical Mechanics: Theory and Experiment, 2007 (08): P08024, 2007. 10.1088/1742-5468/2007/08/p08024.
https://doi.org/10.1088/1742-5468/2007/08/p08024

[31] M. B. Hastings and T. Koma. Spectral gap and exponential decay of correlations. Communications in Mathematical Physics, 265 (3): 781–804, 2006. 10.1007/s00220-006-0030-4.
https://doi.org/10.1007/s00220-006-0030-4

[32] K. Hepp and E. H. Lieb. On the superradiant phase transition for molecules in a quantized radiation field: the Dicke maser model. Annals of Physics, 76 (2): 360–404, 1973. https://doi.org/10.1016/0003-4916(73)90039-0.
https://doi.org/10.1016/0003-4916(73)90039-0

[33] T. Holstein. Studies of polaron motion: Part I. the molecular-crystal model. Annals of Physics, 8 (3): 325–342, 1959. https://doi.org/10.1016/0003-4916(59)90002-8.
https://doi.org/10.1016/0003-4916(59)90002-8

[34] J. Hubbard. Electron correlations in narrow energy bands. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 276 (1365): 238–257, 1963. 10.1098/rspa.1963.0204.
https://doi.org/10.1098/rspa.1963.0204

[35] W. J. Huggins, S. McArdle, T. E. O’Brien, J. Lee, N. C. Rubin, S. Boixo, K. B. Whaley, R. Babbush, and J. R. McClean. Virtual distillation for quantum error mitigation. Phys. Rev. X, 11: 041036, Nov 2021. 10.1103/PhysRevX.11.041036. URL https://link.aps.org/doi/10.1103/PhysRevX.11.041036.
https://doi.org/10.1103/PhysRevX.11.041036

[36] S. P. Jordan, K. S. Lee, and J. Preskill. Quantum algorithms for quantum field theories. Science, 336 (6085): 1130–1133, 2012. 10.1126/science.1217069.
https://doi.org/10.1126/science.1217069

[37] S. P. Jordan, K. S. Lee, and J. Preskill. Quantum computation of scattering in scalar quantum field theories. Quantum Information & Computation, 14 (11-12): 1014–1080, 2014. 10.5555/2685155.2685163.
https://doi.org/10.5555/2685155.2685163

[38] A. Kan and Y. Nam. Lattice quantum chromodynamics and electrodynamics on a universal quantum computer. arXiv preprint arXiv:2107.12769, 2021. 10.48550/arXiv.2107.12769.
https://doi.org/10.48550/arXiv.2107.12769
arXiv:2107.12769

[39] I. D. Kivlichan, J. McClean, N. Wiebe, C. Gidney, A. Aspuru-Guzik, G. K.-L. Chan, and R. Babbush. Quantum simulation of electronic structure with linear depth and connectivity. Physical Review Letters, 120 (11): 110501, 2018. 10.1103/PhysRevLett.120.110501.
https://doi.org/10.1103/PhysRevLett.120.110501

[40] N. Klco and M. J. Savage. Digitization of scalar fields for quantum computing. Physical Review A, 99 (5): 052335, 2019. 10.1103/PhysRevA.99.052335.
https://doi.org/10.1103/PhysRevA.99.052335

[41] N. Klco, E. F. Dumitrescu, A. J. McCaskey, T. D. Morris, R. C. Pooser, M. Sanz, E. Solano, P. Lougovski, and M. J. Savage. Quantum-classical computation of Schwinger model dynamics using quantum computers. Physical Review A, 98 (3): 032331, 2018. 10.1103/PhysRevA.98.032331.
https://doi.org/10.1103/PhysRevA.98.032331

[42] N. Klco, M. J. Savage, and J. R. Stryker. Su(2) non-abelian gauge field theory in one dimension on digital quantum computers. Physical Review D, 101 (7): 074512, 2020. 10.1103/PhysRevD.101.074512.
https://doi.org/10.1103/PhysRevD.101.074512

[43] B. Kloss, D. R. Reichman, and R. Tempelaar. Multiset matrix product state calculations reveal mobile Franck-Condon excitations under strong Holstein-type coupling. Physical Review Letters, 123 (12): 126601, 2019. 10.1103/PhysRevLett.123.126601.
https://doi.org/10.1103/PhysRevLett.123.126601

[44] J. Kogut and L. Susskind. Hamiltonian formulation of Wilson’s lattice gauge theories. Physical Review D, 11 (2): 395, 1975. 10.1103/PhysRevD.11.395.
https://doi.org/10.1103/PhysRevD.11.395

[45] S. Kühn, E. Zohar, J. I. Cirac, and M. C. Bañuls. Non-Abelian string breaking phenomena with matrix product states. Journal of High Energy Physics, 2015 (7): 1–26, 2015. 10.1007/JHEP07(2015)130.
https://doi.org/10.1007/JHEP07(2015)130

[46] J. Liu and Y. Xin. Quantum simulation of quantum field theories as quantum chemistry. Journal of High Energy Physics, 2020 (12): 11, Dec 2020. ISSN 1029-8479. 10.1007/JHEP12(2020)011.
https://doi.org/10.1007/JHEP12(2020)011

[47] S. Lloyd. Universal quantum simulators. Science, 273 (5278): 1073–1078, 1996. 10.1126/science.273.5278.1073.
https://doi.org/10.1126/science.273.5278.1073

[48] G. H. Low and I. L. Chuang. Optimal Hamiltonian simulation by quantum signal processing. Physical Review Letters, 118 (1): 010501, 2017. 10.1103/physrevlett.118.010501.
https://doi.org/10.1103/physrevlett.118.010501

[49] G. H. Low and I. L. Chuang. Hamiltonian simulation by qubitization. Quantum, 3: 163, 2019. 10.22331/q-2019-07-12-163.
https://doi.org/10.22331/q-2019-07-12-163

[50] G. H. Low and N. Wiebe. Hamiltonian simulation in the interaction picture. arXiv preprint arXiv:1805.00675, 2018. 10.48550/arXiv.1805.00675.
https://doi.org/10.48550/arXiv.1805.00675
arXiv:1805.00675

[51] A. Macridin, P. Spentzouris, J. Amundson, and R. Harnik. Digital quantum computation of fermion-boson interacting systems. Physical Review A, 98 (4), 2018a. 10.1103/PhysRevA.98.042312.
https://doi.org/10.1103/PhysRevA.98.042312

[52] A. Macridin, P. Spentzouris, J. Amundson, and R. Harnik. Electron-phonon systems on a universal quantum computer. Physical Review Letters, 121 (11), 2018b. 10.1103/PhysRevLett.121.110504.
https://doi.org/10.1103/PhysRevLett.121.110504

[53] G. Magnifico, T. Felser, P. Silvi, and S. Montangero. Lattice quantum electrodynamics in $(3+1)$-dimensions at finite density with tensor networks. Nature Communications, 12 (1): 1–13, 2021. 10.1038/s41467-021-23646-3.
https://doi.org/10.1038/s41467-021-23646-3

[54] S. McArdle, X. Yuan, and S. Benjamin. Error-mitigated digital quantum simulation. Physical Review Letters, 122: 180501, May 2019. 10.1103/PhysRevLett.122.180501.
https://doi.org/10.1103/PhysRevLett.122.180501

[55] A. H. Moosavian, J. R. Garrison, and S. P. Jordan. Site-by-site quantum state preparation algorithm for preparing vacua of fermionic lattice field theories. arXiv preprint arXiv:1911.03505, 2019. 10.48550/arXiv.1911.03505.
https://doi.org/10.48550/arXiv.1911.03505
arXiv:1911.03505

[56] C. Muschik, M. Heyl, E. Martinez, T. Monz, P. Schindler, B. Vogell, M. Dalmonte, P. Hauke, R. Blatt, and P. Zoller. U(1) Wilson lattice gauge theories in digital quantum simulators. New Journal of Physics, 19 (10): 103020, 2017. 10.1088/1367-2630/aa89ab.
https://doi.org/10.1088/1367-2630/aa89ab

[57] B. Nachtergaele and R. Sims. Lieb-Robinson bounds and the exponential clustering theorem. Communications in Mathematical Physics, 265 (1): 119–130, 2006. 10.1007/s00220-006-1556-1.
https://doi.org/10.1007/s00220-006-1556-1

[58] B. Nachtergaele, H. Raz, B. Schlein, and R. Sims. Lieb-Robinson bounds for harmonic and anharmonic lattice systems. Communications in Mathematical Physics, 286 (3): 1073–1098, 2009. 10.1007/s00220-008-0630-2.
https://doi.org/10.1007/s00220-008-0630-2

[59] P. Otte. Boundedness properties of fermionic operators. Journal of Mathematical Physics, 51 (8): 083503, 2010. 10.1063/1.3464264.
https://doi.org/10.1063/1.3464264

[60] T. Pichler, M. Dalmonte, E. Rico, P. Zoller, and S. Montangero. Real-time dynamics in U(1) lattice gauge theories with tensor networks. Physical Review X, 6 (1): 011023, 2016. 10.1103/PhysRevX.6.011023.
https://doi.org/10.1103/PhysRevX.6.011023

[61] A. Rajput, A. Roggero, and N. Wiebe. Hybridized methods for quantum simulation in the interaction picture. Quantum, 6: 780, 2022. 10.22331/q-2022-08-17-780.
https://doi.org/10.22331/q-2022-08-17-780

[62] T. E. Reinhard, U. Mordovina, C. Hubig, J. S. Kretchmer, U. Schollwöck, H. Appel, M. A. Sentef, and A. Rubio. Density-matrix embedding theory study of the one-dimensional Hubbard-Holstein model. Journal of chemical theory and computation, 15 (4): 2221–2232, 2019. 10.1021/acs.jctc.8b01116.
https://doi.org/10.1021/acs.jctc.8b01116

[63] B. Şahinoğlu and R. D. Somma. Hamiltonian simulation in the low-energy subspace. npj Quantum Information, 7 (1): 119, Jul 2021. ISSN 2056-6387. 10.1038/s41534-021-00451-w.
https://doi.org/10.1038/s41534-021-00451-w

[64] B. Sandhoefer and G. K.-L. Chan. Density matrix embedding theory for interacting electron-phonon systems. Physical Review B, 94 (8): 085115, 2016. 10.1103/PhysRevB.94.085115.
https://doi.org/10.1103/PhysRevB.94.085115

[65] N. P. D. Sawaya, M. Smelyanskiy, J. R. McClean, and A. Aspuru-Guzik. Error sensitivity to environmental noise in quantum circuits for chemical state preparation. Journal of Chemical Theory and Computation, 12 (7): 3097–3108, 2016. 10.1021/acs.jctc.6b00220.
https://doi.org/10.1021/acs.jctc.6b00220

[66] N. P. D. Sawaya, T. Menke, T. H. Kyaw, S. Johri, A. Aspuru-Guzik, and G. G. Guerreschi. Resource-efficient digital quantum simulation of $d$-level systems for photonic, vibrational, and spin-$s$ Hamiltonians. npj Quantum Information, 6 (1): 49, Jun 2020. ISSN 2056-6387. 10.1038/s41534-020-0278-0.
https://doi.org/10.1038/s41534-020-0278-0

[67] F. A. Schröder and A. W. Chin. Simulating open quantum dynamics with time-dependent variational matrix product states: Towards microscopic correlation of environment dynamics and reduced system evolution. Physical Review B, 93 (7): 075105, 2016. 10.1103/PhysRevB.93.075105.
https://doi.org/10.1103/PhysRevB.93.075105

[68] P. Sen. Achieving the Han-Kobayashi inner bound for the quantum interference channel by sequential decoding. arXiv preprint arXiv:1109.0802, 2011. 10.48550/arXiv.1109.0802.
https://doi.org/10.48550/arXiv.1109.0802
arXiv:1109.0802

[69] A. F. Shaw, P. Lougovski, J. R. Stryker, and N. Wiebe. Quantum algorithms for simulating the lattice Schwinger model. Quantum, 4: 306, 2020. 10.22331/q-2020-08-10-306.
https://doi.org/10.22331/q-2020-08-10-306

[70] R. D. Somma. Quantum simulations of one dimensional quantum systems. arXiv preprint arXiv:1503.06319, 2015. 10.48550/arXiv.1503.06319.
https://doi.org/10.48550/arXiv.1503.06319
arXiv:1503.06319

[71] Y. Su, H.-Y. Huang, and E. T. Campbell. Nearly tight Trotterization of interacting electrons. Quantum, 5: 495, 2021. 10.22331/q-2021-07-05-495.
https://doi.org/10.22331/q-2021-07-05-495

[72] M. Suzuki. Decomposition formulas of exponential operators and Lie exponentials with some applications to quantum mechanics and statistical physics. Journal of Mathematical Physics, 26 (4): 601–612, 1985. 10.1063/1.526596.
https://doi.org/10.1063/1.526596

[73] M. C. Tran, Y. Su, D. Carney, and J. M. Taylor. Faster digital quantum simulation by symmetry protection. PRX Quantum, 2: 010323, Feb 2021. 10.1103/PRXQuantum.2.010323.
https://doi.org/10.1103/PRXQuantum.2.010323

[74] F. Verstraete and J. I. Cirac. Mapping local Hamiltonians of fermions to local Hamiltonians of spins. Journal of Statistical Mechanics: Theory and Experiment, 2005 (09): P09012, 2005. 10.1088/1742-5468/2005/09/p09012.
https://doi.org/10.1088/1742-5468/2005/09/p09012

[75] U.-J. Wiese. Ultracold quantum gases and lattice systems: quantum simulation of lattice gauge theories. Annalen der Physik, 525 (10-11): 777–796, 2013. https://doi.org/10.1002/andp.201300104.
https://doi.org/10.1002/andp.201300104

[76] M. P. Woods, M. Cramer, and M. B. Plenio. Simulating bosonic baths with error bars. Physical Review Letters, 115 (13): 130401, 2015. 10.1103/PhysRevLett.115.130401.
https://doi.org/10.1103/PhysRevLett.115.130401

[77] E. Zohar, J. I. Cirac, and B. Reznik. Simulating compact quantum electrodynamics with ultracold atoms: Probing confinement and nonperturbative effects. Physical Review Letters, 109 (12): 125302, 2012. 10.1103/PhysRevLett.109.125302.
https://doi.org/10.1103/PhysRevLett.109.125302

[78] E. Zohar, J. I. Cirac, and B. Reznik. Cold-atom quantum simulator for SU(2) Yang-Mills lattice gauge theory. Physical Review Letters, 110 (12): 125304, 2013. 10.1103/PhysRevLett.110.125304.
https://doi.org/10.1103/PhysRevLett.110.125304

Cited by

[1] Christian W. Bauer, Zohreh Davoudi, A. Baha Balantekin, Tanmoy Bhattacharya, Marcela Carena, Wibe A. de Jong, Patrick Draper, Aida El-Khadra, Nate Gemelke, Masanori Hanada, Dmitri Kharzeev, Henry Lamm, Ying-Ying Li, Junyu Liu, Mikhail Lukin, Yannick Meurice, Christopher Monroe, Benjamin Nachman, Guido Pagano, John Preskill, Enrico Rinaldi, Alessandro Roggero, David I. Santiago, Martin J. Savage, Irfan Siddiqi, George Siopsis, David Van Zanten, Nathan Wiebe, Yukari Yamauchi, Kübra Yeter-Aydeniz, and Silvia Zorzetti, “Quantum Simulation for High Energy Physics”, arXiv:2204.03381.

[2] Angus Kan and Yunseong Nam, “Lattice Quantum Chromodynamics and Electrodynamics on a Universal Quantum Computer”, arXiv:2107.12769.

[3] Anthony N. Ciavarella and Ivan A. Chernyshev, “Preparation of the SU(3) lattice Yang-Mills vacuum with variational quantum methods”, Physical Review D 105 7, 074504 (2022).

[4] Travis S. Humble, Andrea Delgado, Raphael Pooser, Christopher Seck, Ryan Bennink, Vicente Leyton-Ortega, C. -C. Joseph Wang, Eugene Dumitrescu, Titus Morris, Kathleen Hamilton, Dmitry Lyakh, Prasanna Date, Yan Wang, Nicholas A. Peters, Katherine J. Evans, Marcel Demarteau, Alex McCaskey, Thien Nguyen, Susan Clark, Melissa Reville, Alberto Di Meglio, Michele Grossi, Sofia Vallecorsa, Kerstin Borras, Karl Jansen, and Dirk Krücker, “Snowmass White Paper: Quantum Computing Systems and Software for High-energy Physics Research”, arXiv:2203.07091.

[5] Andrei Alexandru, Paulo F. Bedaque, Ruairí Brett, and Henry Lamm, “Spectrum of digitized QCD: Glueballs in a S (1080 ) gauge theory”, Physical Review D 105 11, 114508 (2022).

[6] A. Kan, L. Funcke, S. Kühn, L. Dellantonio, J. Zhang, J. F. Haase, C. A. Muschik, and K. Jansen, “3+1D theta-Term on the Lattice from the Hamiltonian Perspective”, The 38th International Symposium on Lattice Field Theory 112 (2022).

[7] Marius Lemm and Oliver Siebert, “Thermal Area Law for the Bose-Hubbard Model”, arXiv:2207.07760.

[8] Nhung H. Nguyen, Minh C. Tran, Yingyue Zhu, Alaina M. Green, C. Huerta Alderete, Zohreh Davoudi, and Norbert M. Linke, “Digital Quantum Simulation of the Schwinger Model and Symmetry Protection with Trapped Ions”, arXiv:2112.14262.

[9] Tomotaka Kuwahara, Tan Van Vu, and Keiji Saito, “Optimal light cone and digital quantum simulation of interacting bosons”, arXiv:2206.14736.

[10] Abhishek Rajput, Alessandro Roggero, and Nathan Wiebe, “Quantum Error Correction with Gauge Symmetries”, arXiv:2112.05186.

[11] Jiayu Shen, Di Luo, Chenxi Huang, Bryan K. Clark, Aida X. El-Khadra, Bryce Gadway, and Patrick Draper, “Simulating quantum mechanics with a θ -term and an ‘t Hooft anomaly on a synthetic dimension”, Physical Review D 105 7, 074505 (2022).

[12] Manu Mathur and Atul Rathor, “SU (N ) toric code and non-Abelian anyons”, Physical Review A 105 5, 052423 (2022).

[13] Ulysse Chabaud and Saeed Mehraban, “Holomorphic Quantum Computing”, arXiv:2111.00117.

[14] Yao Ji, Henry Lamm, and Shuchen Zhu, “Gluon Digitization via Character Expansion for Quantum Computers”, arXiv:2203.02330.

[15] Nilin Abrahamsen, Yuan Su, Yu Tong, and Nathan Wiebe, “Entanglement area law for 1D gauge theories and bosonic systems”, arXiv:2203.16012.

[16] Yonah Borns-Weil and Di Fang, “Uniform observable error bounds of Trotter formulae for the semiclassical Schrödinger equation”, arXiv:2208.07957.

The above citations are from SAO/NASA ADS (last updated successfully 2022-09-22 15:23:23). The list may be incomplete as not all publishers provide suitable and complete citation data.

Could not fetch Crossref cited-by data during last attempt 2022-09-22 15:23:21: Could not fetch cited-by data for 10.22331/q-2022-09-22-816 from Crossref. This is normal if the DOI was registered recently.

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

Time Stamp: September 22, 2022September 22, 2022

Time Stamp: Dec 7, 2022

Seasonal submission slumber

Source Cluster:

Quantum Journal

Source Node: 1605341

Time Stamp: Aug 2, 2022

Provably accurate simulation of gauge theories and bosonic systems

Republished By Plato

Abstract

► BibTeX data

► References

Cited by

More from Quantum Journal

Dissipation as a resource for Quantum Reservoir Computing

Quantum Alchemy and Universal Orthogonality Catastrophe in One-Dimensional Anyons

Optimizing Variational Quantum Algorithms with qBang: Efficiently Interweaving Metric and Momentum to Navigate Flat Energy Landscapes

Adaptive measurement filter: efficient strategy for optimal estimation of quantum Markov chains

Pauli topological subsystem codes from Abelian anyon theories

A relativistic discrete spacetime formulation of 3+1 QED

An experiment to test the discreteness of time

Random quantum circuits are approximate unitary $t$-designs in depth $Oleft(nt^{5+o(1)}right)$

Variational solutions to fermion-to-qubit mappings in two spatial dimensions

Quantum scattering as a work source

Scaling of the quantum approximate optimization algorithm on superconducting qubit based hardware

Seasonal submission slumber

About Us

Vertical Search & Ai

Platform

Stay Connected

Account