Notação Big O e análise de algoritmo com exemplos de Python

Introdução

Geralmente, existem várias maneiras de resolver o problema usando um programa de computador. Por exemplo, existem várias maneiras de classificar itens em uma matriz - você pode usar mesclar classificação, Tipo de bolha, tipo de inserção, e assim por diante. Todos esses algoritmos têm seus próprios prós e contras e o trabalho do desenvolvedor é pesá-los para poder escolher o melhor algoritmo a ser usado em qualquer caso de uso. Em outras palavras, a questão principal é qual algoritmo usar para resolver um problema específico quando existem várias soluções para o problema.

Análise de algoritmo refere-se à análise da complexidade de diferentes algoritmos e encontrar o algoritmo mais eficiente para resolver o problema em questão. Notação Big-O é uma medida estatística usada para descrever a complexidade do algoritmo.

Neste guia, primeiro faremos uma breve revisão da análise de algoritmos e, em seguida, examinaremos mais detalhadamente a notação Big-O. Veremos como a notação Big-O pode ser usada para encontrar a complexidade do algoritmo com a ajuda de diferentes funções do Python.

Por que a análise de algoritmos é importante?

Para entender por que a análise de algoritmos é importante, vamos usar um exemplo simples. Suponha que um gerente dê uma tarefa a dois de seus funcionários para projetar um algoritmo em Python que calcule o fatorial de um número inserido pelo usuário. O algoritmo desenvolvido pelo primeiro funcionário se parece com isso:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Observe que o algoritmo simplesmente recebe um inteiro como argumento. Dentro de fact() função uma variável chamada product é inicializado para 1. Um loop é executado de 1 para n e durante cada iteração, o valor no product é multiplicado pelo número que está sendo iterado pelo loop e o resultado é armazenado no product variável novamente. Após a execução do loop, o product variável conterá o fatorial.

Da mesma forma, o segundo funcionário também desenvolveu um algoritmo que calcula o fatorial de um número. O segundo funcionário usou uma função recursiva para calcular o fatorial do número n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

O gerente tem que decidir qual algoritmo usar. Para isso, eles decidiram escolher qual algoritmo roda mais rápido. Uma maneira de fazer isso é encontrar o tempo necessário para executar o código na mesma entrada.

No notebook Jupyter, você pode usar o %timeit literal seguido pela chamada de função para encontrar o tempo gasto pela função para executar:

%timeit fact(50)

Isso nos dará:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

A saída diz que o algoritmo leva 9 microssegundos (mais/menos 45 nanossegundos) por loop.

Da mesma forma, podemos calcular quanto tempo a segunda abordagem leva para ser executada:

%timeit fact2(50)

Isso resultará em:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

O segundo algoritmo envolvendo recursão leva 15 microssegundos (mais/menos 427 nanossegundos).

O tempo de execução mostra que o primeiro algoritmo é mais rápido comparado ao segundo algoritmo envolvendo recursão. Ao lidar com grandes entradas, a diferença de desempenho pode se tornar mais significativa.

No entanto, o tempo de execução não é uma boa métrica para medir a complexidade de um algoritmo, pois depende do hardware. Uma métrica de análise de complexidade mais objetiva para um algoritmo é necessária. É aqui que o Notação Big O vem jogar.

Análise de algoritmo com notação Big-O

A notação Big-O significa a relação entre a entrada para o algoritmo e as etapas necessárias para executar o algoritmo. É denotado por um grande “O” seguido por um parêntese de abertura e fechamento. Dentro dos parênteses, a relação entre a entrada e os passos do algoritmo é apresentada usando “n”.

O principal argumento é - Big-O não está interessado em um particular instância em que você executa um algoritmo, como fact(50), mas sim, quão bem ele escada dado entrada crescente. Esta é uma métrica muito melhor para avaliar do que o tempo concreto para uma instância concreta!

Por exemplo, se houver um relação linear entre a entrada e o passo dado pelo algoritmo para completar sua execução, a notação Big-O utilizada será O (n). Da mesma forma, a notação Big-O para funções quadráticas is O (n²).

Para construir a intuição:

• O (n): em n=1, 1 passo é dado. No n=10, 10 passos são dados.
• O (n²): em n=1, 1 passo é dado. No n=10, 100 passos são dados.

At n=1, esses dois teriam o mesmo desempenho! Essa é outra razão pela qual observar a relação entre a entrada e o número de etapas para processar essa entrada é melhor do que apenas avaliar funções com alguma entrada concreta.

A seguir estão algumas das funções Big-O mais comuns:

Nome	Big O
constante	O (c)
Linear	O (n)
Quadrático	O (n²)
Cúbico	O(n³)
Exponencial	O(2ⁿ)
Logarítmico	O (log (n))
Registro Linear	O (nlog (n))

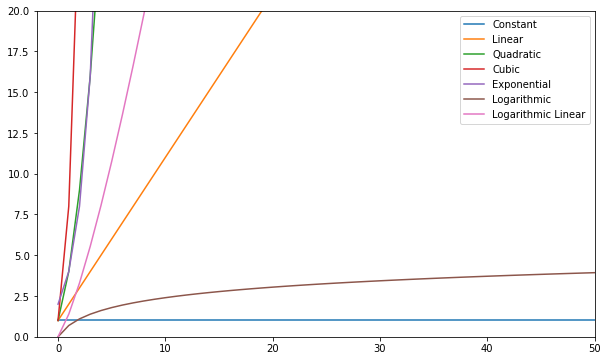
Você pode visualizar essas funções e compará-las:

De um modo geral – qualquer coisa pior que linear é considerada uma complexidade ruim (ou seja, ineficiente) e deve ser evitada, se possível. A complexidade linear é aceitável e geralmente um mal necessário. Logarítmico é bom. Constante é incrível!

Para ter uma ideia de como um Big-O é calculado, vamos dar uma olhada em alguns exemplos de complexidade constante, linear e quadrática.

Complexidade Constante - O(C)

A complexidade de um algoritmo é dita constante se os passos necessários para completar a execução de um algoritmo permanecem constantes, independentemente do número de entradas. A complexidade constante é denotada por O (c) onde c pode ser qualquer número constante.

Vamos escrever um algoritmo simples em Python que encontre o quadrado do primeiro item da lista e o imprima na tela:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

No roteiro acima, independentemente do tamanho de entrada, ou o número de itens na lista de entrada items, o algoritmo executa apenas 2 etapas:

1. Encontrando o quadrado do primeiro elemento
2. Imprimindo o resultado na tela.

Assim, a complexidade permanece constante.

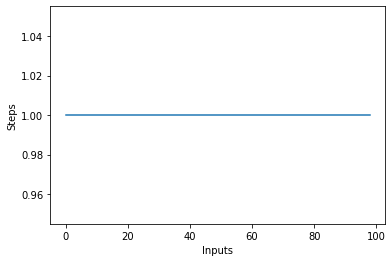
Se você desenhar um gráfico de linha com o tamanho variável do items entrada no eixo X e o número de passos no eixo Y, você obterá uma linha reta. Vamos criar um pequeno script para nos ajudar a visualizar isso. Não importa o número de entradas, o número de passos executados permanece o mesmo:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Complexidade linear - O (n)

A complexidade de um algoritmo é dita linear se os passos necessários para completar a execução de um algoritmo aumentam ou diminuem linearmente com o número de entradas. A complexidade linear é denotada por O (n).

Neste exemplo, vamos escrever um programa simples que exibe todos os itens da lista no console:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

A complexidade do linear_algo() A função é linear no exemplo acima, pois o número de iterações do loop for será igual ao tamanho da entrada items ordem. Por exemplo, se houver 4 itens no items list, o loop for será executado 4 vezes.

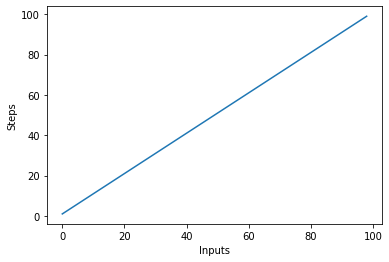
Vamos criar rapidamente um gráfico para o algoritmo de complexidade linear com o número de entradas no eixo x e o número de etapas no eixo y:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Isso resultará em:

Uma coisa importante a notar é que com grandes entradas, as constantes tendem a perder valor. É por isso que normalmente removemos constantes da notação Big-O, e uma expressão como O(2n) geralmente é encurtada para O(n). Tanto O(2n) quanto O(n) são lineares – a relação linear é o que importa, não o valor concreto. Por exemplo, vamos modificar o linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Existem dois loops for que iteram sobre a entrada items Lista. Portanto, a complexidade do algoritmo torna-se O (2n), no entanto, no caso de itens infinitos na lista de entrada, o dobro do infinito ainda é igual ao infinito. Podemos ignorar a constante 2 (uma vez que, em última análise, é insignificante) e a complexidade do algoritmo permanece O (n).

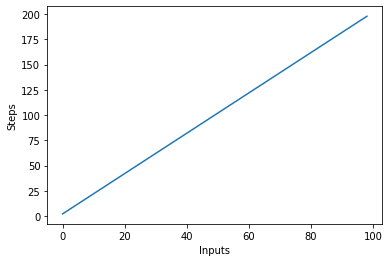
Vamos visualizar este novo algoritmo plotando as entradas no eixo X e o número de etapas no eixo Y:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

No script acima, você pode ver claramente que y=2n, no entanto, a saída é linear e se parece com isso:

Complexidade Quadrática - O (n²)

A complexidade de um algoritmo é dita quadrática quando os passos necessários para executar um algoritmo são uma função quadrática do número de itens na entrada. A complexidade quadrática é denotada como O (n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Temos um loop externo que itera por todos os itens da lista de entrada e, em seguida, um loop interno aninhado, que novamente itera por todos os itens da lista de entrada. O número total de etapas executadas é n*n, onde n é o número de itens na matriz de entrada.

O gráfico a seguir plota o número de entradas em relação às etapas para um algoritmo com complexidade quadrática:

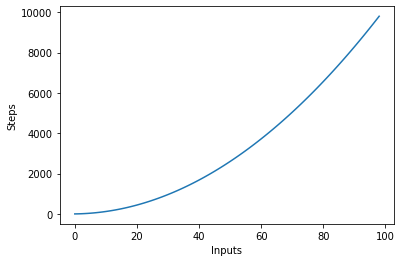
Complexidade logarítmica - O (logn)

Alguns algoritmos atingem complexidade logarítmica, como Pesquisa binária. Binary Search procura por um elemento em uma matriz, verificando o meio de uma matriz e podando a metade em que o elemento não está. Ele faz isso novamente para a metade restante e continua as mesmas etapas até que o elemento seja encontrado. Em cada passo, é metades o número de elementos na matriz.

Isso requer que a matriz seja classificada e que façamos uma suposição sobre os dados (como que ela esteja classificada).

Quando você pode fazer suposições sobre os dados recebidos, pode executar etapas que reduzem a complexidade de um algoritmo. A complexidade logarítmica é desejável, pois alcança um bom desempenho mesmo com entrada altamente dimensionada.

Encontrando a complexidade das funções complexas?

Nos exemplos anteriores, tínhamos funções bastante simples na entrada. No entanto, como calculamos o Big-O de funções que chamam (várias) outras funções na entrada?

Vamos dar uma olhada:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

No script acima várias tarefas estão sendo executadas, primeiro, uma string é impressa 5 vezes no console usando o print declaração. Em seguida, imprimimos a lista de entrada duas vezes na tela e, finalmente, outra string é impressa três vezes no console. Para encontrar a complexidade de tal algoritmo, precisamos dividir o código do algoritmo em partes e tentar encontrar a complexidade das partes individuais. Anote a complexidade de cada peça.

Na primeira seção temos:

for i in range(5):
	print("Python is awesome")

A complexidade desta parte é O (5) já que cinco etapas constantes estão sendo executadas neste pedaço de código, independentemente da entrada.

A seguir, temos:

for item in items:
	print(item)

Sabemos que a complexidade do código acima é O (n). Da mesma forma, a complexidade do seguinte trecho de código também é O (n):

for item in items:
	print(item)

Finalmente, no trecho de código a seguir, uma string é impressa três vezes, portanto, a complexidade é O (3):

print("Big O")
print("Big O")
print("Big O")

Para encontrar a complexidade geral, basta adicionar essas complexidades individuais:

O(5) + O(n) + O(n) + O(3)

Simplificando o acima temos:

O(8) + O(2n) = O(8+2n)

Dissemos anteriormente que quando a entrada (que tem comprimento n neste caso) se torna extremamente grande, as constantes se tornam insignificantes, ou seja, duas ou metade do infinito ainda permanece infinito. Portanto, podemos ignorar as constantes. A complexidade final do algoritmo será O (n)!

Complexidade de pior x melhor caso

Normalmente, quando alguém pergunta sobre a complexidade de um algoritmo – eles estão interessados ​​na complexidade do pior caso (Big-O). Às vezes, eles também podem estar interessados ​​na complexidade do melhor caso (Big-Omega).

Para entender a relação entre eles, vamos dar uma olhada em outro pedaço de código:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

No script acima, temos uma função que recebe um número e uma lista de números como entrada. Retorna verdadeiro se o número passado for encontrado na lista de números, caso contrário, retorna None. Se você procurar 2 na lista, ele será encontrado na primeira comparação. Esta é a melhor complexidade do algoritmo em que o item pesquisado é encontrado no primeiro índice pesquisado. A melhor complexidade de caso, neste caso, é O (1). Por outro lado, se você pesquisar 10, ele será encontrado no último índice pesquisado. O algoritmo terá que pesquisar em todos os itens da lista, portanto a complexidade do pior caso torna-se O (n).

Além da complexidade de melhor e pior caso, você também pode calcular a complexidade média (Big-Theta) de um algoritmo, que lhe diz “dada uma entrada aleatória, qual é a complexidade de tempo esperada do algoritmo”?

Complexidade do Espaço

Além da complexidade de tempo, onde você conta o número de passos necessários para completar a execução de um algoritmo, também pode encontrar o complexidade do espaço que se refere à quantidade de espaço que você precisa alocar na memória durante a execução de um programa.

Dê uma olhada no seguinte exemplo:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

A return_squares() A função aceita uma lista de inteiros e retorna uma lista com os quadrados correspondentes. O algoritmo deve alocar memória para o mesmo número de itens da lista de entrada. Portanto, a complexidade de espaço do algoritmo torna-se O (n).

Conclusão

A notação Big-O é a métrica padrão usada para medir a complexidade de um algoritmo. Neste guia, estudamos o que é a notação Big-O e como ela pode ser usada para medir a complexidade de uma variedade de algoritmos. Também estudamos diferentes tipos de funções Big-O com a ajuda de diferentes exemplos em Python. Por fim, revisamos brevemente a complexidade do pior e do melhor caso, juntamente com a complexidade do espaço.