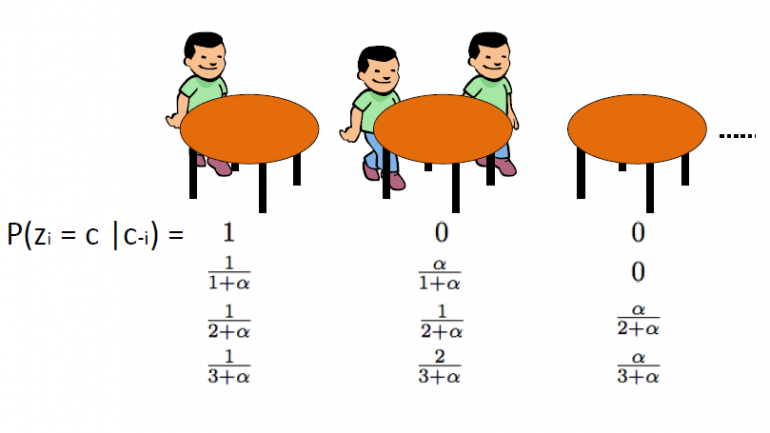O processo Dirichlet, o processo de restaurante chinês e outras representações

• 20 de maio de 2014
• Vasilis Vryniotis
• . Sem comentários

Este artigo é a terceira parte da série Clustering with Dirichlet Process Mixture Models. Na vez anterior, definimos o Modelo de Mistura Finita com base na Distribuição de Dirichlet e colocamos questões sobre como podemos tornar esse modelo específico infinito. Discutimos brevemente a ideia de tomar o limite do modelo quando o número k de clusters tende ao infinito, mas como enfatizamos a existência de tal objeto não é trivial (em outras palavras, como nós realmente “tomamos o limite de um modelo ”?). Como lembrete, a razão pela qual queremos tornar k infinito é porque desta forma teremos um modelo não paramétrico que não nos obriga a predefinir o número total de clusters dentro dos dados.

Atualização: O Datumbox Machine Learning Framework agora é de código aberto e gratuito para download. Confira o pacote com.datumbox.framework.machinelearning.clustering para ver a implementação de Modelos de Mistura de Processo Dirichlet em Java.

Embora nosso objetivo seja construir um modelo capaz de realizar clustering em conjuntos de dados, antes disso devemos discutir sobre os Processos Dirichlet. Forneceremos tanto as definições matemáticas estritas quanto as explicações mais intuitivas do DP e discutiremos maneiras de construir o processo. Essas construções/representações podem ser vistas como uma forma de encontrar ocorrências do Processo Dirichlet na “vida real”.

Apesar do fato de eu ter tentado adaptar meu relatório de pesquisa de forma que essas postagens do blog sejam mais fáceis de seguir, ainda é importante definir as ferramentas e distribuições matemáticas necessárias antes de começarmos a usar os modelos. Os modelos de Processo de Dirichlet são um tópico de pesquisa ativa, mas exigem um bom entendimento de Estatística e Processos Estocásticos antes de usá-los. Outro problema é que, como veremos neste artigo, os Processos Dirichlet podem ser representados/construídos de várias maneiras. Como resultado, vários trabalhos acadêmicos usam notações/convenções completamente diferentes e examinam o problema de diferentes pontos de vista. Neste post eu tento explicá-los da forma mais simples possível e usar a mesma notação. Esperamos que as coisas fiquem mais claras com os dois próximos artigos que se concentram na definição dos Modelos de Mistura de Processo de Dirichlet e em como realmente usá-los para realizar a análise de cluster.

1. Definição do Processo Dirichlet

Um processo de Dirichlet sobre um espaço Θ é um processo estocástico. É uma distribuição de probabilidade sobre “distribuições de probabilidade sobre o espaço Θ” e uma extrair dele é uma distribuição discreta. Mais formalmente, uma distribuição de Dirichlet é uma distribuição sobre medidas de probabilidade. UMA medida de probabilidade é uma função de subconjuntos do espaço Θ a [0,1]. G é uma medida de probabilidade aleatória distribuída DP, denotada como , se para qualquer partição (A₁,…UMA_n) do espaço Θ temos que .

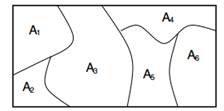
Figura 1: As margens em partições finitas são distribuídas por Dirichlet.

O DP tem dois parâmetros: O primeiro é a distribuição de base G₀ que serve como meio . O segundo é o parâmetro de força α que é estritamente positivo e serve como variância inversa . Determina a extensão da repetição dos valores da distribuição de saída. Quanto maior o valor de a, menor a repetição; quanto menor o valor, maior a repetição dos valores da distribuição do produto. Finalmente, o espaço Θ é o espaço de parâmetros no qual definimos o DP. Além disso, o espaço Θ é também o espaço de definição de G₀ que é a mesma de G.

Mais simples e maneira intuitiva para explicar um processo de Dirichlet é o seguinte. Suponha que temos um espaço Θ que pode ser particionado de qualquer maneira finita (A₁,…,UMA_n) e uma distribuição de probabilidade G que atribui probabilidades a eles. O G é uma distribuição de probabilidade específica sobre Θ, mas existem muitas outras. O Processo Dirichlet em Θ modela exatamente isso; é uma distribuição sobre todas as distribuições de probabilidade possíveis no espaço Θ. O processo de Dirichlet é parametrizado com o G₀ função base e o parâmetro de concentração α. Podemos dizer que G é distribuído de acordo com DP com parâmetros α e G₀ se a distribuição conjunta das probabilidades que G atribui às partições de Θ segue a Distribuição de Dirichlet. Alternativamente, podemos dizer que as probabilidades que G atribui a qualquer partição finita de Θ seguem a Distribuição de Dirichlet.

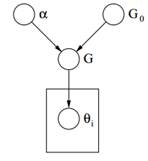
Figura 2: Modelo Gráfico do Processo Dirichlet

Finalmente acima podemos ver o modelo gráfico de um DP. Devemos notar que α é um hiperparâmetro escalar, G₀ é a distribuição base de DP, G uma distribuição aleatória sobre Θ espaço de parâmetros amostrado do DP que atribui probabilidades aos parâmetros e θ_i é um vetor de parâmetros que é extraído da distribuição G e é um elemento do espaço Θ.

2. Processos Dirichlet Posteriores

Os Processos Dirichlet Posteriores foram discutidos por Ferguson. Começamos desenhando uma medida de probabilidade aleatória G de um processo de Dirichlet, . Como G é uma distribuição de probabilidade sobre Θ, também podemos amostrar dessa distribuição e extrair amostras independentes identicamente distribuídas θ₁,…,θ_n ~ G. Como os desenhos de um processo de Dirichlet são distribuições discretas, podemos representar onde é uma notação curta para que é uma função delta que leva 1 se e 0 em outro lugar. Um efeito interessante disso é que, como G é definido dessa maneira, há uma probabilidade positiva de diferentes amostras terem o mesmo valor . Como veremos mais adiante, isso cria um efeito de cluster que pode ser usado para realizar a Análise de Cluster em conjuntos de dados.

Usando as definições e observações acima, queremos estimar a posterior do Processo de Dirichlet dadas as amostras θ. No entanto, uma vez que sabemos que e usando as Regras de Bayes e a Conjugação entre Dirichlet e Multinomial temos que e .

Equação 1: Processo Dirichlet Posterior

Esta propriedade é muito importante e é utilizada pelas várias representações DP.

3. Representações do Processo Dirichlet

Nos segmentos anteriores definimos o Processo de Dirichlet e apresentamos seu modelo teórico. Uma questão importante que devemos responder é como sabemos que tal objeto existe e como podemos construir e representar um processo de Dirichlet.

Os primeiros indícios de existência foram fornecidos por Ferguson que utilizou o Teorema da Consistência de Kolmogorov, deu a definição de um Processo de Dirichlet e descreveu o Processo de Dirichlet Posterior. Continuando sua pesquisa, Blackwell e MacQueen usou o Teorema de Finetti para provar a existência de tal medida de probabilidade aleatória e introduziu o esquema de urnas de Blackwell-MacQueen que satisfaz as propriedades do Processo de Dirichlet. Em 1994 Sethuraman forneceu uma maneira adicional simples e direta de construir um DP, introduzindo a construção de quebra-pau. Por fim, outra representação foi fornecida por Aldous que introduziu o Processo de Restaurante Chinês como uma forma eficaz de construir um Processo Dirichlet.

As várias Representações do Processo de Dirichlet são matematicamente equivalentes, mas sua formulação difere porque examinam o problema de diferentes pontos de vista. Abaixo apresentamos as representações mais comuns encontradas na literatura e focamos no Processo de Restaurante Chinês que fornece uma maneira simples e computacionalmente eficiente de construir algoritmos de inferência para o Processo de Dirichlet.

3.1 O esquema de urnas Blackwell-MacQueen

O esquema de urnas Blackwell-MacQueen pode ser usado para representar um processo de Dirichlet e foi introduzido por Blackwell e MacQueen. Baseia-se no esquema de urnas de Pólya que pode ser visto como o modelo oposto de amostragem sem reposição. No esquema da urna Pólya assumimos que temos uma urna não transparente que contém bolas coloridas e as desenhamos aleatoriamente. Quando desenhamos uma bola, observamos sua cor, a colocamos de volta na urna e adicionamos mais uma bola da mesma cor. Um esquema semelhante é usado por Blackwell e MacQueen para construir um Processo Dirichlet.

Este esquema produz uma sequência de θ₁, θ₂,… com probabilidades condicionais . Neste esquema assumimos que G₀ é uma distribuição sobre cores e cada θ_n representa a cor da bola que é colocada na urna. o algoritmo é como se segue:

· Começamos com uma urna vazia.

· Com probabilidade proporcional a α nos desenhamos e adicionamos uma bola desta cor na urna.

· Com probabilidade proporcional a n-1, extraímos uma bola aleatória da urna, observamos sua cor, a colocamos de volta na urna e adicionamos uma bola adicional da mesma cor na urna.

Anteriormente, começamos com um processo de Dirichlet e derivamos o esquema Blackwell-MacQueen. Agora vamos começar inversamente a partir do esquema Blackwell-MacQueen e derivar o DP. Desde θ_i foram extraídas de uma maneira iid de G, sua distribuição conjunta será invariante a quaisquer permutações finitas e, portanto, elas são permutáveis. Consequentemente, usando o teorema de de Finetti, temos que deve existir uma distribuição sobre medidas para torná-las iid e essa distribuição é o Processo de Dirichlet. Como resultado provamos que o esquema de urnas Blackwell-MacQueen é uma representação do DP e nos dá uma forma concreta de construí-lo. Como veremos mais adiante, esse esquema é matematicamente equivalente ao Processo do Restaurante Chinês.

3.2 A construção de quebra-varetas

A construção Stick-breaking é uma forma alternativa de representar um Processo Dirichlet que foi introduzido por Sethuraman. É uma forma construtiva de formar o distribuição e utiliza o seguinte analogia: Assumimos que temos uma vara de comprimento 1, a quebramos na posição β₁ e atribuímos π₁ igual ao comprimento da parte da vara que quebramos. Repetimos o mesmo processo para obter π₂, Pi₃,… etc; devido à forma como este esquema é definido, podemos continuar a fazê-lo infinitas vezes.

Com base no acima, o π_k pode ser modelado como , Onde o enquanto que nos esquemas anteriores os θ são amostrados diretamente pela distribuição Base . Consequentemente, a distribuição G pode ser escrita como uma soma de funções delta ponderadas com π_k probabilidades iguais a . Assim, a construção de quebra de varas nos dá uma maneira simples e intuitiva de construir um processo de Dirichlet.

3.3 O Processo do Restaurante Chinês

O Processo de Restaurante Chinês, que foi introduzido por Aldous, é outra forma eficaz de representar um Processo Dirichlet e pode ser diretamente ligado ao esquema de urnas Blackwell-MacQueen. Este esquema utiliza o seguinte analogia: Assumimos que existe um restaurante chinês com infinitas mesas. À medida que os clientes entram no restaurante, sentam-se aleatoriamente em qualquer uma das mesas ocupadas ou escolhem sentar-se na primeira mesa vazia disponível.

O CRP define uma distribuição no espaço de partições dos inteiros positivos. Começamos desenhando θ₁,…θ_n do esquema de urnas Blackwell-MacQueen. Como discutimos nos segmentos anteriores, esperamos ver um efeito de agrupamento e, portanto, o número total de valores únicos de θ k será significativamente menor que n. Assim, isso define uma partição do conjunto {1,2,…,n} em k clusters. Consequentemente, o desenho do esquema de urnas de Blackwell-MacQueen induz uma partição aleatória do conjunto {1,2,…,n}. O processo do restaurante chinês é induzido distribuição sobre partições. O algoritmo é o seguinte:

· Começamos com um restaurante vazio.

· The 1^st cliente senta-se sempre em 1^st mesa

· O n+1^th cliente tem 2 opções:

o Sente-se na 1ª mesa desocupada com probabilidade

o Sente-se em qualquer uma das k-ésimas mesas ocupadas com probabilidade
onde é o número de pessoas sentadas naquela mesa

Onde α é o valor de dispersão de DP e n é o número total de clientes no restaurante em um determinado momento. A variável latente z_i armazena o número da tabela do i^th cliente e assume valores de 1 a k_n onde k_n é o número total de mesas ocupadas quando n clientes estão no restaurante. Devemos notar que k_n será sempre menor ou igual a n e, em média, é cerca de . Finalmente, devemos notar que a probabilidade de arranjo da mesa é invariante às permutações. Assim o z_i é permutável, o que implica que mesas com o mesmo tamanho de clientes tenham a mesma probabilidade.

O Processo do Restaurante Chinês está fortemente ligado ao esquema de urnas Pólya e ao Processo Dirichlet. O CRP é uma forma de especificar um distribuição sobre partições (atribuições de tabela) de n pontos e pode ser usado como prior no espaço da variável latente z_i qual determina as atribuições de cluster. O CRP é equivalente ao esquema de urnas da Pólya com a única diferença de não atribuir parâmetros a cada tabela/cluster. Ir do CRP ao esquema de urnas da Pólya nos desenhamos para todas as tabelas k=1,2… e então para cada x_i que está agrupado na tabela z_i atribuir um . Em outras palavras, atribua ao novo x_i o parâmetro θ da tabela. Finalmente desde não podemos atribuir o θ para mesas infinitas desde o início, podemos simplesmente atribuir um novo θ toda vez que alguém se senta em uma nova mesa. Devido a tudo isso, o CRP pode nos ajudar a construir algoritmos computacionalmente eficientes para realizar Análise de Cluster em conjuntos de dados.

Neste post, discutimos o Processo Dirichlet e várias maneiras de construí-lo. Usaremos as idéias acima no próximo artigo. Apresentaremos o Modelo de Mistura do Processo Dirichlet e usaremos a Representação do Restaurante Chinês para construir o Processo Dirichlet e pré-formar a Análise de Cluster. Se você perdeu alguns pontos, não se preocupe, pois as coisas começarão a ficar mais claras com os próximos dois artigos.

Espero que tenha achado este post interessante. Se você fez, reserve um momento para compartilhá-lo no Facebook e no Twitter. 🙂