Обозначение Big O и анализ алгоритмов на примерах Python

Введение

Обычно существует несколько способов решения проблемы с помощью компьютерной программы. Например, есть несколько способов сортировки элементов в массиве — вы можете использовать Сортировка слиянием, пузырьковая сортировка, сортировка вставок, и так далее. Все эти алгоритмы имеют свои плюсы и минусы, и задача разработчика состоит в том, чтобы взвесить их, чтобы иметь возможность выбрать лучший алгоритм для использования в любом случае использования. Другими словами, главный вопрос заключается в том, какой алгоритм использовать для решения конкретной проблемы, когда существует несколько решений проблемы.

Алгоритм анализа относится к анализу сложности различных алгоритмов и поиску наиболее эффективного алгоритма для решения поставленной задачи. Биг-О нотация статистическая мера, используемая для описания сложности алгоритма.

В этом руководстве мы сначала сделаем краткий обзор алгоритмического анализа, а затем более подробно рассмотрим нотацию Big-O. Мы увидим, как можно использовать нотацию Big-O для определения сложности алгоритма с помощью различных функций Python.

Почему алгоритмический анализ важен?

Чтобы понять, почему анализ алгоритма важен, мы воспользуемся помощью простого примера. Предположим, менеджер дает задание двум своим сотрудникам разработать алгоритм на языке Python, вычисляющий факториал числа, введенного пользователем. Алгоритм, разработанный первым сотрудником, выглядит так:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Обратите внимание, что алгоритм просто принимает целое число в качестве аргумента. Внутри fact() функция переменная с именем product инициализируется 1. Цикл выполняется из 1 в n и во время каждой итерации значение в product умножается на число, повторяемое циклом, и результат сохраняется в product снова переменная. После выполнения цикла product переменная будет содержать факториал.

Точно так же второй сотрудник также разработал алгоритм, вычисляющий факториал числа. Второй сотрудник использовал рекурсивную функцию для вычисления факториала числа. n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Менеджер должен решить, какой алгоритм использовать. Для этого они решили выбрать, какой алгоритм работает быстрее. Один из способов сделать это — найти время, необходимое для выполнения кода на том же входе.

В блокноте Jupyter вы можете использовать %timeit литерал, за которым следует вызов функции, чтобы найти время, затраченное функцией на выполнение:

%timeit fact(50)

Это даст нам:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Вывод говорит, что алгоритм принимает 9 микросекунд (плюс/минус 45 наносекунд) на цикл.

Точно так же мы можем рассчитать, сколько времени требуется для выполнения второго подхода:

%timeit fact2(50)

Это приведет к:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Второй алгоритм, включающий рекурсию, принимает 15 микросекунд (плюс/минус 427 наносекунд).

Время выполнения показывает, что первый алгоритм быстрее по сравнению со вторым алгоритмом, включающим рекурсию. При работе с большими входными данными разница в производительности может стать более значительной.

Однако время выполнения не является хорошей метрикой для измерения сложности алгоритма, поскольку оно зависит от аппаратного обеспечения. Необходим более объективный показатель анализа сложности алгоритма. Вот где Обозначение Big O приходит играть

Алгоритмический анализ с нотацией Big-O

Обозначение Big-O означает связь между входными данными алгоритма и шагами, необходимыми для выполнения алгоритма. Он обозначается большой буквой «О», за которой следуют открывающая и закрывающая скобки. В скобках связь между входными данными и шагами, предпринятыми алгоритмом, представлена ​​с помощью «n».

Главный вывод: Big-O не заинтересован в особый экземпляр, в котором вы запускаете алгоритм, например fact(50), а скорее, насколько хорошо это лестница при увеличении ввода. Это гораздо лучшая метрика для оценки, чем конкретное время для конкретного экземпляра!

Например, если есть линейная зависимость между вводом и шагом, предпринятым алгоритмом для завершения его выполнения, используемая нотация Big-O будет О (п). Точно так же обозначение Big-O для квадратичные функции is O (n²).

Для развития интуиции:

• О (п): в n=1, сделан 1 шаг. В n=10, сделано 10 шагов.
• O (n²): в n=1, сделан 1 шаг. В n=10, сделано 100 шагов.

At n=1, эти двое будут работать одинаково! Это еще одна причина, по которой наблюдение за взаимосвязью между входными данными и количеством шагов для обработки этих входных данных лучше, чем просто оценка функций с некоторыми конкретными входными данными.

Ниже приведены некоторые из наиболее распространенных функций Big-O:

Фамилия	Большой О
постоянная	O (c)
Линейные приводы	О (п)
квадратный	O (n²)
Кубический	О (п³)
Экспоненциальный	О (2ⁿ)
логарифмический	O (журнал (п))
Лог линейный	O (nlog (n))

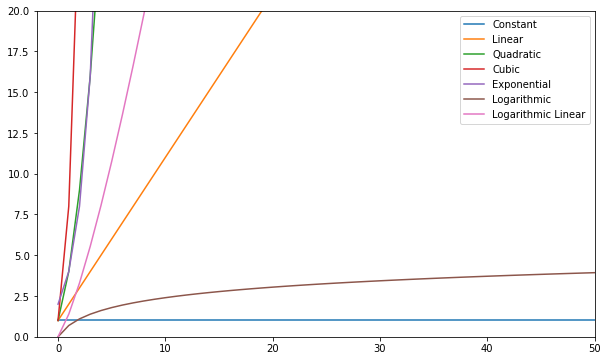
Вы можете визуализировать эти функции и сравнить их:

Вообще говоря, все, что хуже линейного, считается плохой сложностью (т.е. неэффективной), и его следует по возможности избегать. Линейная сложность — это нормально, и обычно это неизбежное зло. Логарифмический - это хорошо. Константа восхитительна!

Чтобы получить представление о том, как вычисляется Big-O, давайте рассмотрим несколько примеров постоянной, линейной и квадратичной сложности.

Постоянная сложность – О (С)

Сложность алгоритма называется постоянной, если количество шагов, необходимых для завершения выполнения алгоритма, остается постоянным, независимо от количества входных данных. Постоянная сложность обозначается O (c) в котором c может быть любым постоянным числом.

Давайте напишем простой алгоритм на Python, который находит квадрат первого элемента в списке, а затем выводит его на экран:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

В приведенном выше сценарии независимо от размера ввода, или количество элементов во входном списке items, алгоритм выполняет всего 2 шага:

1. Нахождение квадрата первого элемента
2. Вывод результата на экран.

Таким образом, сложность остается неизменной.

Если вы нарисуете линейный график с переменным размером items введите по оси X и количество шагов по оси Y, вы получите прямую линию. Давайте создадим короткий сценарий, который поможет нам визуализировать это. Независимо от количества входов, количество выполненных шагов остается неизменным:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

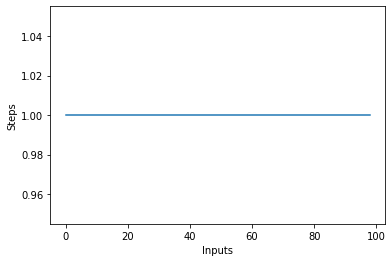
Линейная сложность – О (п)

Сложность алгоритма называется линейной, если количество шагов, необходимых для завершения выполнения алгоритма, увеличивается или уменьшается линейно с количеством входных данных. Линейная сложность обозначается О (п).

В этом примере давайте напишем простую программу, которая выводит все элементы списка на консоль:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Сложность linear_algo() функция является линейной в приведенном выше примере, поскольку количество итераций цикла for будет равно размеру ввода items массив. Например, если в списке 4 элемента. items list, цикл for будет выполнен 4 раза.

Давайте быстро создадим график для алгоритма линейной сложности с количеством входных данных по оси x и количеством шагов по оси y:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Это приведет к:

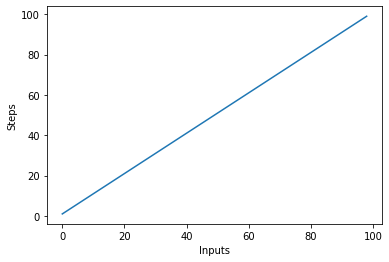
Важно отметить, что при больших входных данных константы имеют тенденцию терять ценность. Вот почему мы обычно удаляем константы из нотации Big-O, а такое выражение, как O(2n), обычно сокращается до O(n). И O(2n), и O(n) являются линейными — важна линейная зависимость, а не конкретное значение. Например, изменим linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Есть два цикла for, которые перебирают входные данные. items список. Поэтому сложность алгоритма становится O (2n), однако в случае бесконечных элементов во входном списке удвоение бесконечности по-прежнему равно бесконечности. Мы можем игнорировать константу 2 (поскольку это в конечном счете несущественно) и сложность алгоритма остается О (п).

Давайте визуализируем этот новый алгоритм, отложив входные данные по оси X и количество шагов по оси Y:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

В приведенном выше сценарии вы можете ясно видеть, что у=2n, однако вывод линейный и выглядит так:

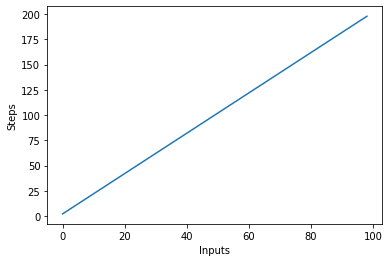
Квадратичная сложность – O (n²)

Говорят, что сложность алгоритма является квадратичной, когда шаги, необходимые для выполнения алгоритма, являются квадратичной функцией количества элементов во входных данных. Квадратичная сложность обозначается как O (n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

У нас есть внешний цикл, который перебирает все элементы входного списка, а затем вложенный внутренний цикл, который снова перебирает все элементы входного списка. Общее количество выполненных шагов равно n*n, где n — количество элементов во входном массиве.

На следующем графике показано количество входных данных в зависимости от шагов для алгоритма с квадратичной сложностью:

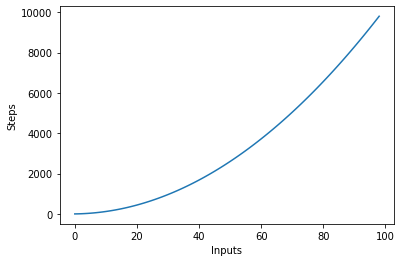
Логарифмическая сложность – O (LOGN)

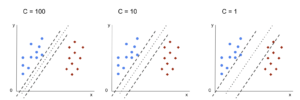
Некоторые алгоритмы достигают логарифмической сложности, например Бинарный поиск. Двоичный поиск ищет элемент в массиве, проверяя средний массива и обрезка половины, в которой элемента нет. Он делает это снова для оставшейся половины и продолжает те же шаги, пока элемент не будет найден. На каждом шагу это половинки количество элементов в массиве.

Это требует, чтобы массив был отсортирован, и чтобы мы сделали предположение о данных (например, что они отсортированы).

Когда вы можете делать предположения о входящих данных, вы можете предпринять шаги, которые уменьшат сложность алгоритма. Логарифмическая сложность желательна, так как она обеспечивает хорошую производительность даже при сильно масштабированном вводе.

Нахождение сложности сложных функций?

В предыдущих примерах у нас на входе были довольно простые функции. Однако, как мы вычисляем Big-O функций, которые вызывают (множество) других функций на входе?

Давайте взглянем:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

В приведенном выше скрипте выполняются несколько задач, во-первых, строка печатается 5 раз на консоли с помощью команды print утверждение. Далее мы дважды выводим список ввода на экран, и, наконец, еще одна строка выводится трижды на консоль. Чтобы найти сложность такого алгоритма, нам нужно разбить код алгоритма на части и попытаться найти сложность отдельных частей. Отметьте сложность каждой части.

В первом разделе имеем:

for i in range(5):
	print("Python is awesome")

Сложность этой части O (5) поскольку в этом фрагменте кода выполняются пять постоянных шагов независимо от ввода.

Далее у нас есть:

for item in items:
	print(item)

Мы знаем, что сложность приведенного выше фрагмента кода О (п). Точно так же сложность следующего фрагмента кода также О (п):

for item in items:
	print(item)

Наконец, в следующем фрагменте кода строка печатается три раза, следовательно, сложность O (3):

print("Big O")
print("Big O")
print("Big O")

Чтобы найти общую сложность, нам просто нужно добавить эти отдельные сложности:

O(5) + O(n) + O(n) + O(3)

Упрощая вышеизложенное, получаем:

O(8) + O(2n) = O(8+2n)

Ранее мы говорили, что когда вход (который в данном случае имеет длину n) становится чрезвычайно большим, константы становятся незначительными, т.е. удвоенная или половина бесконечности по-прежнему остается бесконечностью. Поэтому мы можем игнорировать константы. Окончательная сложность алгоритма будет О (п)!

Наихудшая и наилучшая сложность случая

Обычно, когда кто-то спрашивает вас о сложности алгоритма, его интересует сложность в наихудшем случае (Big-O). Иногда их может интересовать и наилучшая сложность (Big-Omega).

Чтобы понять взаимосвязь между ними, давайте взглянем на другой фрагмент кода:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

В приведенном выше сценарии у нас есть функция, которая принимает число и список чисел в качестве входных данных. Возвращает true, если переданное число найдено в списке чисел, иначе возвращает None. Если вы ищете 2 в списке, он будет найден в первом сравнении. Это наилучшая сложность алгоритма, поскольку искомый элемент находится в первом искомом индексе. Лучшая сложность случая, в данном случае O (1). С другой стороны, если вы ищете 10, он будет найден в последнем искомом индексе. Алгоритму придется искать все элементы в списке, следовательно наихудшая сложность становится О (п).

В дополнение к лучшей и худшей сложности, вы также можете рассчитать средняя сложность (Big-Theta) алгоритма, который говорит вам: «Учитывая случайный ввод, какова ожидаемая временная сложность алгоритма»?

Космическая сложность

В дополнение к временной сложности, когда вы подсчитываете количество шагов, необходимых для завершения выполнения алгоритма, вы также можете найти сложность пространства который относится к количеству места, которое вам нужно выделить в памяти во время выполнения программы.

Взгляните на следующий пример:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

Ассоциация return_squares() функция принимает список целых чисел и возвращает список с соответствующими квадратами. Алгоритм должен выделить память для того же количества элементов, что и во входном списке. Следовательно, пространственная сложность алгоритма становится О (п).

Заключение

Нотация Big-O — это стандартная метрика, используемая для измерения сложности алгоритма. В этом руководстве мы изучили, что такое нотация Big-O и как ее можно использовать для измерения сложности различных алгоритмов. Мы также изучили различные типы функций Big-O с помощью различных примеров Python. Наконец, мы кратко рассмотрели наихудшую и наилучшую сложность случаев, а также пространственную сложность.