Повышенная точность моделирования рысака с использованием интерполяции Чебышева

Повышенная точность моделирования рысака с использованием интерполяции Чебышева

Отметка времени: 26 февраля 2024 г., 9:34 AM

Гумаро Рендон1, Джейкоб Уоткинс2, и Натан Вибе3,4

1Zapata Computing Inc., Бостон, Массачусетс 02110, США
2Установка для пучков редких изотопов, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824, США
3Департамент компьютерных наук, Университет Торонто, Торонто, ON M5S 2E4, Канада
4Тихоокеанская северо-западная национальная лаборатория, Ричленд, Вашингтон, 99352, США

Находите эту статью интересной или хотите обсудить? Scite или оставить комментарий на SciRate.

Абстрактные

Квантовая метрология позволяет измерять свойства квантовой системы в оптимальном пределе Гейзенберга. Однако когда соответствующие квантовые состояния готовятся с использованием цифрового гамильтонового моделирования, накопленные алгоритмические ошибки приведут к отклонениям от этого фундаментального предела. В этой работе мы показываем, как можно уменьшить алгоритмические ошибки, возникающие из-за троттеризованной временной эволюции, с помощью стандартных методов полиномиальной интерполяции. Наш подход заключается в экстраполяции до нулевого размера шага Троттера, что похоже на методы экстраполяции с нулевым шумом для уменьшения аппаратных ошибок. Мы проводим строгий анализ ошибок интерполяционного подхода для оценки собственных значений и временных ожиданий и показываем, что предел Гейзенберга достигается с точностью до полилогарифмических коэффициентов ошибки. Наша работа предполагает, что точность, приближающаяся к точности современных алгоритмов моделирования, может быть достигнута с использованием только Троттера и классических ресурсов для ряда соответствующих алгоритмических задач.

Повышенная точность моделирования Троттера с использованием интерполяции Чебышева. PlatoBlockchain Data Intelligence. Вертикальный поиск. Ай.

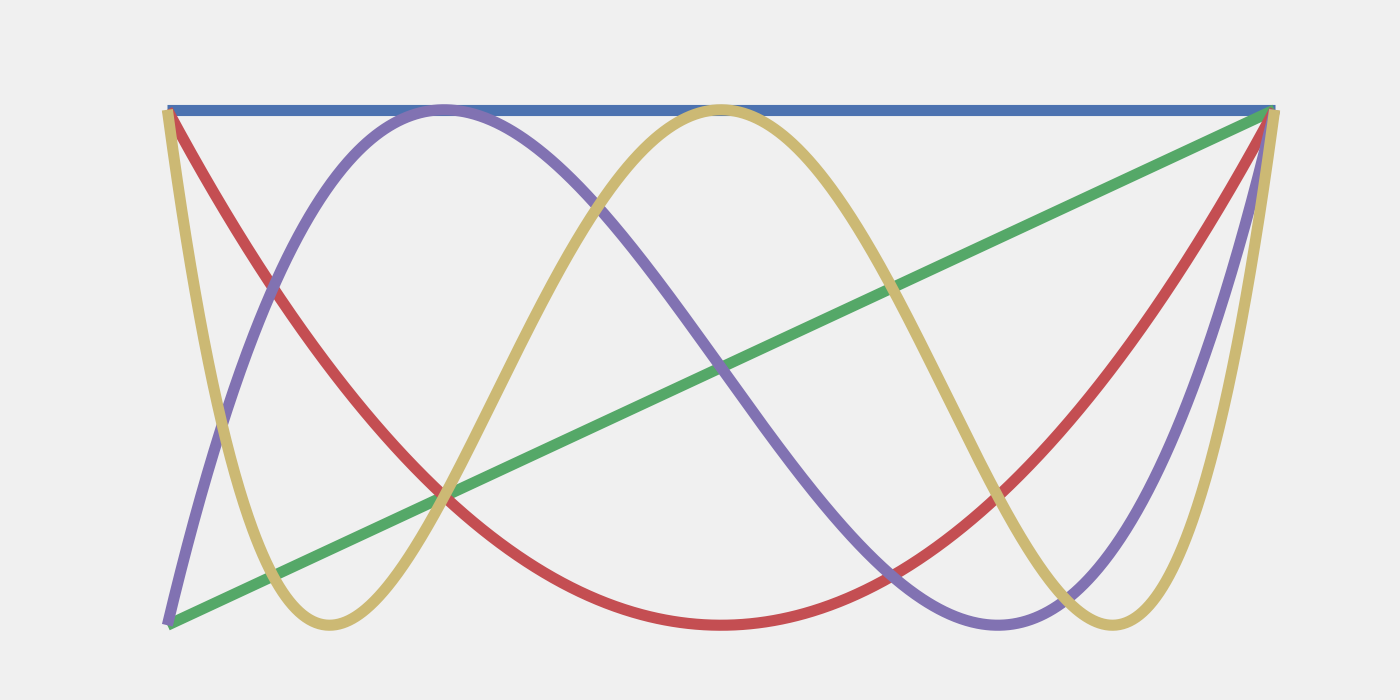
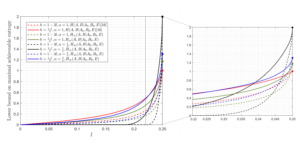
Рекомендованное изображение: первые пять полиномов Чебышева. Интерполяция по нулям Чебышева служит надежной схемой уменьшения ошибок Троттера.

[Встраиваемое содержимое]

Популярное резюме

Квантовые компьютеры могут улучшить наше понимание химии, материалов, ядерной физики и других научных дисциплин за счет усовершенствованного квантового моделирования. Для этой задачи существует несколько доступных квантовых алгоритмов, и среди них часто отдают предпочтение формулам Троттера из-за их простоты и низких первоначальных затрат. К сожалению, формулы Троттера теоретически относительно неточны по сравнению с их более новыми и более сложными конкурентами. Хотя увеличение вычислительного времени может помочь, эта стратегия быстро становится неуправляемой на современных шумных квантовых устройствах с ограниченной способностью выполнять длительные непрерывные вычисления.

Чтобы уменьшить ошибки в моделировании Троттера без увеличения времени квантовой обработки, мы используем полиномы, чтобы изучить взаимосвязь между ошибкой и размером шага. Собирая данные для различных вариантов размера шага, мы можем интерполировать, то есть объединять данные с полиномом, а затем оценить ожидаемое поведение для очень маленьких размеров шага. Мы доказываем математически, что наш подход дает асимптотическое улучшение точности по сравнению со стандартным Троттером для двух фундаментальных задач: оценки собственных значений и оценки значений ожидания.

Наш метод прост и практичен, требует только стандартных методов квантовых и классических вычислений. Мы считаем, что наша работа обеспечивает прочную теоретическую основу для дальнейших исследований алгоритмического устранения ошибок. Расширение этой работы может происходить в нескольких направлениях: от устранения искусственных предположений в нашем анализе до демонстрации улучшенного квантового моделирования.

► Данные BibTeX

► Рекомендации

[1] С. Ллойд, Универсальные квантовые симуляторы, Science 273 (1996) 1073.
https: / / doi.org/ 10.1126 / science.273.5278.1073

[2] М. Райхер, Н. Вибе, К. М. Своре, Д. Векер и М. Тройер, Выяснение механизмов реакции на квантовых компьютерах, Труды Национальной академии наук 114 (2017) 7555.
https: / / doi.org/ 10.1073 / pnas.161915211

[3] Дж. Д. Уитфилд, Дж. Биамонте и А. Аспуру-Гузик, Моделирование гамильтонианов электронной структуры с использованием квантовых компьютеров, Молекулярная физика 109 (2011) 735.
https: / / doi.org/ 10.1080 / 00268976.2011.552441

[4] Дж. Ли, Д. У. Берри, К. Гидни, У. Дж. Хаггинс, Дж. Р. МакКлин, Н. Вибе и др., Еще более эффективные квантовые химические вычисления посредством тензорного гиперсокращения, PRX Quantum 2 (2021) 030305.
https: / / doi.org/ 10.1103 / PRXQuantum.2.030305

[5] В. фон Бург, Г.Х. Лоу, Т. Ханер, Д.С. Штайгер, М. Райхер, М. Реттелер и др., Вычислительный катализ, усиленный квантовыми вычислениями, Physical Review Research 3 (2021) 033055.
https: / / doi.org/ 10.1103 / PhysRevResearch.3.033055

[6] С. П. Джордан, К. С. Ли и Дж. Прескилл, Квантовые алгоритмы для квантовых теорий поля, Science 336 (2012) 1130.
https: / / doi.org/ 10.1126 / science.1217069

[7] А. Ф. Шоу, П. Луговски, Дж. Р. Страйкер и Н. Вибе, Квантовые алгоритмы для моделирования решеточной модели Швингера, Quantum 4 (2020) 306.
https:/​/​doi.org/​10.22331/​q-2020-08-10-306

[8] Н. Клко, М. Дж. Сэвидж и Дж. Р. Страйкер, Су (2) неабелева калибровочная теория поля в одном измерении на цифровых квантовых компьютерах, Physical Review D 101 (2020) 074512.
https: / / doi.org/ 10.1103 / PhysRevD.101.074512

[9] А. М. Чайлдс и Н. Вибе, гамильтоново моделирование с использованием линейных комбинаций унитарных операций, Quantum Info. Вычислить. 12 (2012) 901–924.
https: / / doi.org/ 10.26421 / QIC12.11-12-1

[10] Г.Х. Лоу, В. Ключников и Н. Вибе, Хорошо обусловленное многопродуктное гамильтоновое моделирование, arXiv:1907.11679 (2019).
https://​/​doi.org/​10.48550/​arXiv.1907.11679
Arxiv: 1907.11679

[11] Д. У. Берри, А. М. Чайлдс, Р. Клив, Р. Котари и Р. Д. Сомма, Моделирование гамильтоновой динамики с помощью усеченного ряда Тейлора, Physical Review Letters 114 (2015) 090502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.090502

[12] Г.Х. Лоу и Н. Вибе, Гамильтоновое моделирование в картине взаимодействия, arXiv:1805.00675 (2018).
https://​/​doi.org/​10.48550/​arXiv.1805.00675
Arxiv: 1805.00675

[13] М. Киферова, А. Шерер и Д. У. Берри, Моделирование динамики нестационарных гамильтонианов с помощью усеченного ряда Дайсона, Physical Review A 99 (2019) 042314.
https: / / doi.org/ 10.1103 / PhysRevA.99.042314

[14] Г.Х. Лоу и И.Л. Чуанг, Гамильтоновское моделирование путем кубитизации, Quantum 3 (2019) 163.
https:/​/​doi.org/​10.22331/​q-2019-07-12-163

[15] Р. Бэббуш, К. Гидни, Д. В. Берри, Н. Вибе, Дж. МакКлин, А. Палер и др., Кодирование электронных спектров в квантовых схемах с линейной t-сложностью, Physical Review X 8 (2018) 041015.
https: / / doi.org/ 10.1103 / PhysRevX.8.041015

[16] Д. В. Берри, Г. Ахокас, Р. Клив и Б. С. Сандерс, Эффективные квантовые алгоритмы для моделирования разреженных гамильтонианов, Communications in Mathematical Physics 270 (2006) 359–371.
HTTPS: / / doi.org/ 10.1007 / s00220-006-0150-х

[17] Н. Вибе, Д. В. Берри, П. Хойер и Б. С. Сандерс, Моделирование квантовой динамики на квантовом компьютере, Журнал физики A: Mathematical and Theoretical 44 (2011) 445308.
https:/​/​doi.org/​10.1088/​1751-8113/​44/​44/​445308

[18] А. М. Чайлдс, Ю. Су, М. К. Тран, Н. Вибе и С. Чжу, Теория ошибки рысака с масштабированием коммутатора, Physical Review X 11 (2021) 011020.
https: / / doi.org/ 10.1103 / PhysRevX.11.011020

[19] Дж. Хаах, М.Б. Гастингс, Р. Котари и Г.Х. Лоу, Квантовый алгоритм для моделирования эволюции гамильтонианов решетки в реальном времени, SIAM Journal on Computing (2021) FOCS18.
https: / / doi.org/ 10.1137 / 18M12315

[20] М. Хаган и Н. Вибе, Композитное квантовое моделирование, arXiv:2206.06409 (2022).
https:/​/​doi.org/​10.22331/​q-2023-11-14-1181
Arxiv: 2206.06409

[21] Г.Х. Лоу, Ю. Су, Ю. Тонг и М. К. Тран, О сложности выполнения шагов рыси, arXiv:2211.09133 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.4.020323
Arxiv: 2211.09133

[22] Г.Х. Лоу и И.Л. Чуанг, Оптимальное гамильтониановое моделирование с помощью квантовой обработки сигналов, Physical Review Letters 118 (2017).
https: / / doi.org/ 10.1103 / physrevlett.118.010501

[23] С. Эндо, К. Чжао, Ю. Ли, С. Бенджамин и К. Юань, Уменьшение алгоритмических ошибок в гамильтоновом моделировании, Phys. Ред. А 99 (2019) 012334.
https: / / doi.org/ 10.1103 / PhysRevA.99.012334

[24] А. С. Васкес, Р. Хиптмайр и С. Вернер, Улучшение алгоритма квантовых линейных систем с использованием экстраполяции Ричардсона, Транзакции ACM на квантовых вычислениях 3 (2022).
https: / / doi.org/ 10.1145 / 3490631

[25] А.С. Васкес, Д.Д. Эггер, Д. Окснер и С. Вернер, Хорошо обусловленные многопродуктовые формулы для аппаратного гамильтонового моделирования, Quantum 7 (2023) 1067.
https:/​/​doi.org/​10.22331/​q-2023-07-25-1067

[26] М. Судзуки, Общая теория фрактальных интегралов по траекториям с приложениями к теориям многих тел и статистической физике, Журнал математической физики 32 (1991) 400.
https: / / doi.org/ 10.1063 / 1.529425

[27] А. Гильен, Ю. Су, Г. Х. Лоу и Н. Вибе, Квантовое преобразование сингулярных значений и не только: экспоненциальные улучшения квантовой матричной арифметики, в материалах 51-го ежегодного симпозиума ACM SIGACT по теории вычислений, стр. 193–204, 2019 г. , ДОИ.
https: / / doi.org/ 10.1145 / 3313276.3316366

[28] К. Йи и Э. Кроссон, Спектральный анализ формул произведения для квантового моделирования, npj Quantum Information 8 (2022) 37.
HTTPS: / / doi.org/ 10.1038 / s41534-022-00548-ш

[29] А. Квартерони, Р. Сакко и Ф. Салери, Численная математика, том. 37, Springer Science & Business Media (2010), 10.1007/​b98885.
https: / / doi.org/ 10.1007 / b98885

[30] Ф. Пиаццон и М. Вианелло, Неравенства устойчивости для констант Лебега с помощью марковских неравенств, Исследовательские заметки Dolomites по аппроксимации 11 (2018).

[31] А. П. де Камарго, О числовой устойчивости формулы Ньютона для интерполяции Лагранжа, Журнал вычислительной и прикладной математики 365 (2020) 112369.
https: // doi.org/ 10.1016 / j.cam.2019.112369

[32] Л. Трефетен, Шесть мифов о полиномиальной интерполяции и квадратуре (2011).

[33] В. Гаучи, Насколько (не)стабильны системы Вандермонда? асимптотический и вычислительный анализ, в «Конспектах лекций по чистой и прикладной математике», стр. 193–210, Marcel Dekker, Inc, 1990.

[34] Н. Дж. Хайэм, Численная устойчивость барицентрической лагранжевой интерполяции, IMA Journal of Numerical Analysis 24 (2004) 547.
https://​/​doi.org/​10.1093/​imanum/​24.4.547

[35] Дж. К. Мейсон и Д. С. Хэндскомб, Полиномы Чебышева, CRC press (2002), 10.1201/​9781420036114.
https: / / doi.org/ 10.1201 / 9781420036114

[36] Г. Рендон, Т. Изубучи и Ю. Кикучи, Влияние окна сужения косинуса на оценку квантовой фазы, Physical Review D 106 (2022) 034503.
https: / / doi.org/ 10.1103 / PhysRevD.106.034503

[37] Л. Н. Трефетен, Теория приближений и практика приближений, расширенное издание, SIAM (2019), 10.1137/​1.9781611975949.
https: / / doi.org/ 10.1137 / 1.9781611975949

[38] Ф. Л. Бауэр и К. Т. Фике, Нормы и теоремы исключения, Numer. Математика. 2 (1960) 137–141.
https: / / doi.org/ 10.1007 / BF01386217

[39] С. Бланес, Ф. Касас, Ж.-А. Отео и Дж. Рос, Расширение Магнуса и некоторые его применения, Physics report 470 (2009) 151.
https: / / doi.org/ 10.1016 / j.physrep.2008.11.001

[40] Н. Клко и М. Дж. Сэвидж, Подготовка минимально запутанного состояния локализованных волновых функций на квантовых компьютерах, Physical Review A 102 (2020).
https: / / doi.org/ 10.1103 / physreva.102.012612

[41] Дж. Дж. Гарсия-Риполь, Квантовые алгоритмы многомерного анализа: от интерполяции к уравнениям в частных производных, Quantum 5 (2021) 431.
https:/​/​doi.org/​10.22331/​q-2021-04-15-431

[42] В. Гурецкий, Р. Демкович-Добжански, Х. М. Уайзман и Д. В. Берри, предел Гейзенберга с поправкой на $pi$, Письма о физическом обзоре 124 (2020) 030501.
https: / / doi.org/ 10.1103 / PhysRevLett.124.030501

[43] Д. Гринко, Дж. Гакон, К. Зуфаль и С. Вернер, Итеративная оценка квантовой амплитуды, npj Quantum Information 7 (2021) 52 [1912.05559].
https:/​/​doi.org/​10.1038/​s41534-021-00379-1
Arxiv: 1912.05559

[44] Н. Вибе, Д. Берри, П. Хойер и Б.С. Сандерс, Разложение более высокого порядка упорядоченных операторных экспонент, Journal of Physics A: Mathematical and Theoretical 43 (2010) 065203.
https:/​/​doi.org/​10.1088/​1751-8113/​43/​6/​065203

[45] Р. А. Хорн и К. Р. Джонсон, Матричный анализ, издательство Кембриджского университета (2012), 10.1017/​CBO9780511810817.
https: / / doi.org/ 10.1017 / CBO9780511810817

[46] М. Чиани, Д. Дардари и М. К. Саймон, Новые экспоненциальные границы и приближения для расчета вероятности ошибки в каналах с замиранием, IEEE Transactions on Wireless Communications 2 (2003) 840.
https://​/​doi.org/​10.1109/​TWC.2003.814350

[47] Дж. М. Борвейн и П. Б. Борвейн, Пи и AGM: исследование аналитической теории чисел и вычислительной сложности, Wiley-Interscience (1987).

[48] Б.Л. Хиггинс, Д.В. Берри, С.Д. Бартлетт, Х.М. Уайзман и Г.Дж. Прайд, Оценка фазы без запутывания, ограниченная Гейзенбергом, Nature 450 (2007) 393.
https: / / doi.org/ 10.1038 / nature06257

[49] Р.Б. Гриффитс и К.-С. Ниу, Квазиклассическое преобразование Фурье для квантовых вычислений, Physical Review Letters 76 (1996) 3228.
https: / / doi.org/ 10.1103 / PhysRevLett.76.3228

[50] А.Ю. Китаев, Квантовые измерения и проблема абелева стабилизатора, quant-ph/​9511026 (1995).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9511026
Arxiv: колич-фот / 9511026

[51] Д.С. Абрамс и С. Ллойд, Квантовый алгоритм, обеспечивающий экспоненциальное увеличение скорости для поиска собственных значений и собственных векторов, Physical Review Letters 83 (1999) 5162.
https: / / doi.org/ 10.1103 / PhysRevLett.83.5162

[52] Дж. Уоткинс, Н. Вибе, А. Роджеро и Д. Ли, Зависимое от времени моделирование гамильтониана с использованием конструкций дискретных часов, arXiv:2203.11353 (2022).
https://​/​doi.org/​10.48550/​arXiv.2203.11353
Arxiv: 2203.11353

[53] Т. Д. Але, Точные и простые оценки необработанных моментов биномиального и пуассоновского распределений, Статистика и вероятностные письма 182 (2022) 109306.
https://doi.org/10.1016/j.spl.2021.109306

[54] Т. Ривлин, Полиномы Чебышева, Dover Books on Mathematics, Dover Publications (2020).

Цитируется

[1] Дин Ли, «Квантовые методы решения проблем собственных значений», Европейский физический журнал A 59 11, 275 (2023).

[2] Тацухико Н. Икеда, Хидеки Коно и Кейсуке Фуджи, «Trotter24: адаптивная Троттеризация с гарантированной точностью и шагом для гамильтонового моделирования», Arxiv: 2307.05406, (2023).

[3] Ханс Хон Сан Чан, Ричард Мейстер, Мэтью Л. Го и Балинт Кочор, «Алгоритмическая теневая спектроскопия», Arxiv: 2212.11036, (2022).

[4] Сергей Жук, Найл Робертсон и Сергей Бравый, «Границы ошибки Троттера и динамические формулы с несколькими произведениями для гамильтонового моделирования», Arxiv: 2306.12569, (2023).

[5] Zhicheng Zhang, Qisheng Wang и Mingsheng Ying, «Параллельный квантовый алгоритм для гамильтонового моделирования», Квант 8, 1228 (2024).

[6] Леа М. Тренквальдер, Элеонора Шерри, Томас Э. О'Брайен и Ведран Дунько, «Компиляция гамильтонового моделирования по формуле продукта посредством обучения с подкреплением», Arxiv: 2311.04285, (2023).

[7] Гумаро Рендон и Питер Д. Джонсон, «Оценка энергии гауссовского состояния на малой глубине», Arxiv: 2309.16790, (2023).

[8] Грегори Бойд, «Распараллеливание LCU с низкими издержками с помощью коммутирующих операторов», Arxiv: 2312.00696, (2023).

Приведенные цитаты из САО / НАСА ADS (последнее обновление успешно 2024-02-27 02:40:25). Список может быть неполным, поскольку не все издатели предоставляют подходящие и полные данные о цитировании.

On Цитируемый сервис Crossref Данные о цитировании работ не найдены (последняя попытка 2024-02-27 02:40:24).

Эта статья опубликована в Quantum под Creative Commons Attribution 4.0 International (CC BY 4.0) лицензия. Авторское право остается за первоначальными правообладателями, такими как авторы или их учреждения.

Отметка времени:

Больше от Квантовый журнал