Калибровочная картина квантовой динамики

Калибровочная картина квантовой динамики

Отметка времени: 21 марта 2024 г., 6:43

Кевин Слэгл

Факультет электротехники и вычислительной техники, Университет Райса, Хьюстон, Техас 77005 США
Кафедра физики Калифорнийского технологического института, Пасадена, Калифорния 91125, США
Институт квантовой информации и материи и Институт теоретической физики Уолтера Бёрка, Калифорнийский технологический институт, Пасадена, Калифорния 91125, США

Находите эту статью интересной или хотите обсудить? Scite или оставить комментарий на SciRate.

Абстрактные

Хотя локальные гамильтонианы демонстрируют динамику локального времени, эта локальность не выражена явно в картине Шредингера в том смысле, что амплитуды волновой функции не подчиняются локальному уравнению движения. Мы показываем, что геометрическая локальность может быть достигнута явно в уравнениях движения путем «калибровки» глобальной унитарной инвариантности квантовой механики в локальную калибровочную инвариантность. То есть математические ожидания $langle psi|A|psi rangle$ инвариантны относительно глобального унитарного преобразования, действующего на волновую функцию $|psirangle в U |psirangle$ и операторы $A в UAU^dagger$, и мы показываем, что это возможно преобразовать эту глобальную инвариантность в локальную калибровочную инвариантность. Для этого мы заменим волновую функцию набором локальных волновых функций $|psi_Jrangle$, по одной на каждый участок пространства $J$. Коллекция пространственных патчей подобрана так, чтобы покрыть пространство; например, мы могли бы выбрать, чтобы патчи представляли собой одиночные кубиты или узлы ближайших соседей на решетке. Локальные волновые функции, связанные с соседними парами пространственных участков $I$ и $J$, связаны друг с другом динамическими унитарными преобразованиями $U_{IJ}$. Локальные волновые функции локальны в том смысле, что локальна их динамика. То есть уравнения движения локальных волновых функций $|psi_Jrangle$ и связей $U_{IJ}$ явно локальны в пространстве и зависят только от ближайших гамильтоновых членов. (Локальные волновые функции являются волновыми функциями многих тел и имеют ту же размерность гильбертова пространства, что и обычная волновая функция.) Мы называем эту картину квантовой динамики калибровочной картиной, поскольку она демонстрирует локальную калибровочную инвариантность. Локальная динамика отдельного пространственного участка связана с картиной взаимодействия, где гамильтониан взаимодействия состоит только из близлежащих членов гамильтониана. Мы также можем обобщить явную локальность, включив локальность в локальные плотности заряда и энергии.

Калибровочная картина квантовой динамики PlatoBlockchain Data Intelligence. Вертикальный поиск. Ай.

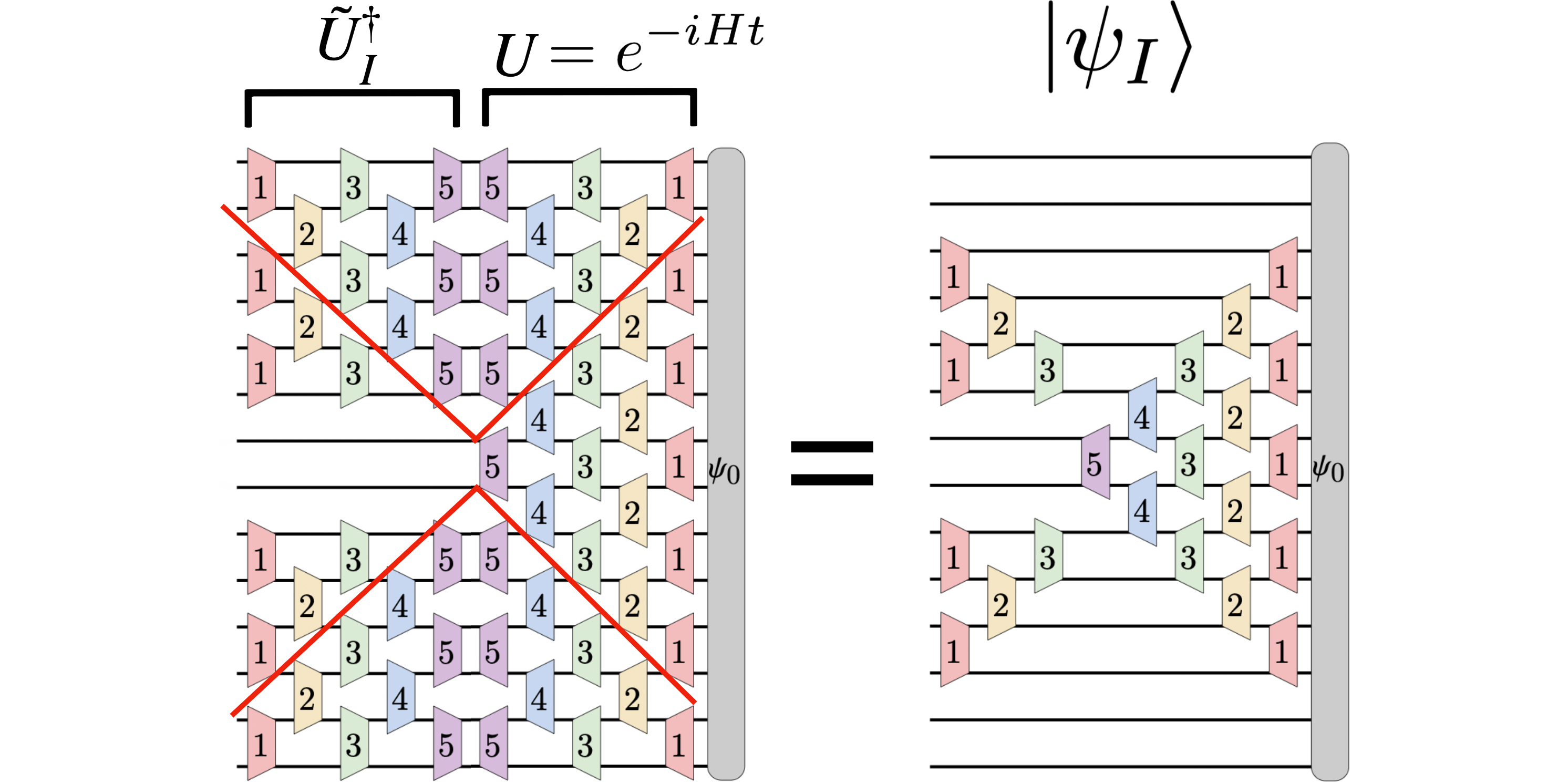
Рекомендованное изображение: На рисунке Шредингера исходная волновая функция $|psi_0rangle$ эволюционирует в $U(t) |psi_0rangle$ через время $t$, где $U(t) = e^{-iHt}$ — унитарная временная эволюция. оператор. Вместо этого калибровочная картина рассматривает локальные волновые функции $|psi_I(t)rangle$, которые связаны с подмножеством (или участком) $I$ в пространстве. Эволюционирующая во времени локальная волновая функция $|psi_I(t)rangle = tilde{U}_I^dagger(t) |psi(t)rangle$ получается из волновой функции Шредингера $|psi(t)rangle = U(t) |psi_0rangle $ через унитарный оператор $tilde{U}_I^dagger(t)$, который обращает эволюцию времени за пределами области $I$. В результате динамика локальной волновой функции $partial_I |psi_I(t)rangle$ зависит только от ближайших членов гамильтониана, которые перекрываются с областью $I$. На рисунке эти унитарные операторы изображены в виде квантовых схем и показано, что большая часть временной эволюции из $U(t)$ компенсируется с помощью $tilde{U}_I^dagger(t)$, оставляя только оператор временной эволюции в форме песочных часов. действующий на исходную волновую функцию (справа на рисунке). Этот оператор в форме песочных часов аналогичен оператору роста в форме светового конуса на картине Гейзенберга.

Популярное резюме

Две самые известные картины квантовой динамики — это картины Шрёдингера и Гейзенберга. В картине Шредингера волновая функция меняется во времени, тогда как в картине Гейзенберга волновая функция постоянна, но операторы меняются во времени. В этой работе мы представляем новую картину квантовой динамики — калибровочную картину, которая глубоко связана с локальностью информации и калибровочной теорией.

Относительно локальности: существенным преимуществом модели Гейзенберга является то, что локальность явно выражена в уравнениях движения. То есть временная эволюция локального оператора зависит только от состояния ближайших локальных операторов. Напротив, в картине Шредингера локальность не выражена явно, для которой существует единственная волновая функция, временная динамика которой зависит от операторов повсюду в пространстве. Наша новая калибровочная картина модифицирует картину Шредингера таким образом, что мы можем вычислить «локальную волновую функцию», которая несет ту же информацию, что и волновая функция Шредингера, ожидая, что временная динамика локальных волновых функций в калибровочной картине зависит только от соседних гамильтоновых членов, что делает локальность явной в уравнения движения. Чтобы добиться этой явной локальности, калибровочная картина добавляет к уравнениям движения калибровочные поля.

Калибровочная теория устанавливает глубокую связь между гамильтонианом (или лагранжианом) с глобальной симметрией и другим гамильтонианом, в котором глобальная симметрия заменяется локальной калибровочной симметрией посредством добавления динамических калибровочных полей. Интересно, что уравнение Шредингера $ihbar parts_t |psirangle = H |psirangle$ допускает глобальную унитарную инвариантность, задаваемую преобразованием $|psirangle в U |psirangle$ и $H в UHU^dagger$. Наша работа показывает, что к этой глобальной инвариантности в уравнении Шрёдингера также можно применить калибровочную теорию, чтобы получить новое уравнение движения, т.е. калибровочную картину, с динамическими калибровочными полями и локальной калибровочной инвариантностью.

► Данные BibTeX

► Рекомендации

[1] Дэвид Дойч и Патрик Хейден. «Информационный поток в запутанных квантовых системах». Труды Лондонского королевского общества, серия A 456, 1759 (2000). arXiv:quant-ph/9906007.
https: / / doi.org/ 10.1098 / rspa.2000.0585
Arxiv: колич-фот / 9906007

[2] Майкл А. Левин и Сяо-Ган Вэнь. «Конденсация струн-сетей: физический механизм топологических фаз». Физ. Ред. Б 71, 045110 (2005). arXiv:cond-mat/​0404617.
https: / / doi.org/ 10.1103 / PhysRevB.71.045110
Arxiv: конд-мат / 0404617

[3] Т. Сентил, Ашвин Вишванат, Леон Баленц, Субир Сачдев и Мэтью П.А. Фишер. «Деопределенные квантовые критические точки». Наука 303, 1490–1494 (2004). arXiv:cond-mat/0311326.
https: / / doi.org/ 10.1126 / science.1091806
Arxiv: конд-мат / 0311326

[4] Бени Йошида. «Экзотический топологический порядок во фрактальных спиновых жидкостях». Физ. Ред. Б 88, 125122 (2013). arXiv: 1302.6248.
https: / / doi.org/ 10.1103 / PhysRevB.88.125122
Arxiv: 1302.6248

[5] Кевин Хартнетт. «Умножение матриц на несколько дюймов ближе к мифической цели». Журнал «Кванта» (2021). URL: https://www.quantamagazine.org/mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/.
https://www.quantamagazine.org/mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​

[6] Фолькер Штрассен. «Исключение по Гауссу не является оптимальным». Численная математика 13, 354–356 (1969).
https: / / doi.org/ 10.1007 / BF02165411

[7] Кевин Слэгл. «Квантовые калибровочные сети: новый вид тензорных сетей». Квант 7, 1113 (2023). arXiv: 2210.12151.
https:/​/​doi.org/​10.22331/​q-2023-09-14-1113
Arxiv: 2210.12151

[8] Роман Орус. «Практическое введение в тензорные сети: состояния матричного произведения и прогнозируемые состояния запутанных пар». Анналы физики 349, 117–158 (2014). arXiv: 1306.2164.
https: / / doi.org/ 10.1016 / j.aop.2014.06.013
Arxiv: 1306.2164

[9] Майкл П. Залетел и Фрэнк Поллманн. «Состояния изометрической тензорной сети в двух измерениях». Физ. Преподобный Летт. 124, 037201 (2020). arXiv: 1902.05100.
https: / / doi.org/ 10.1103 / PhysRevLett.124.037201
Arxiv: 1902.05100

[10] Стивен Вайнберг. «Проверка квантовой механики». Анналы физики 194, 336–386 (1989).
https:/​/​doi.org/​10.1016/​0003-4916(89)90276-5

[11] Н. Гизин. «Нелинейная квантовая механика Вайнберга и сверхсветовая связь». Physics Letters A 143, 1–2 (1990).
https:/​/​doi.org/​10.1016/​0375-9601(90)90786-N

[12] Джозеф Полчински. «Нелинейная квантовая механика Вайнберга и парадокс Эйнштейна-Подольского-Розена». Физ. Преподобный Летт. 66, 397–400 (1991).
https: / / doi.org/ 10.1103 / PhysRevLett.66.397

[13] Кевин Слэгл. «Тестирование квантовой механики с использованием шумных квантовых компьютеров» (2021). arXiv: 2108.02201.
Arxiv: 2108.02201

[14] Брайан Свингл. «Расшифровка физики корреляторов вне временного порядка». Физика природы 14, 988–990 (2018).
https:/​/​doi.org/​10.1038/​s41567-018-0295-5

[15] Игнасио Гарсия-Мата, Родольфо А. Жалаберт и Диего А. Вишняцки. «Корреляторы вневременного порядка и квантовый хаос» (2022). arXiv: 2209.07965.
Arxiv: 2209.07965

[16] Рахул Нандкишор и Дэвид А. Хьюз. «Многочастичная локализация и термализация в квантовой статистической механике». Ежегодный обзор физики конденсированного состояния 6, 15–38 (2015). arXiv: 1404.0686.
https: / / doi.org/ 10.1146 / annurev-conmatphys-031214-014726
Arxiv: 1404.0686

[17] Дмитрий Абанин, Эхуд Альтман, Иммануил Блох и Максим Сербин. «Коллоквиум: многочастичная локализация, термализация и запутанность». Обзоры современной физики 91, 021001 (2019). arXiv: 1804.11065.
https: / / doi.org/ 10.1103 / RevModPhys.91.021001
Arxiv: 1804.11065

[18] Бруно Нахтергаэле и Роберт Симс. «Много шума из-за чего-то: чем полезны границы Либа-Робинсона» (2011). arXiv: 1102.0835.
Arxiv: 1102.0835

[19] Дэниел А. Робертс и Брайан Свингл. «Граница Либа-Робинсона и эффект бабочки в квантовых теориях поля». Физ. Преподобный Летт. 117, 091602 (2016). arXiv: 1603.09298.
https: / / doi.org/ 10.1103 / PhysRevLett.117.091602
Arxiv: 1603.09298

[20] Чжиюань Ван и Каден Р.А. Хаззард. «Усиление связи Либа-Робинсона в локально взаимодействующих системах». PRX Quantum 1, 010303 (2020). arXiv: 1908.03997.
https: / / doi.org/ 10.1103 / PRXQuantum.1.010303
Arxiv: 1908.03997

Цитируется

[1] Саяк Гуха Рой и Кевин Слэгл, «Интерполяция между калибровочной картиной и картиной Шредингера квантовой динамики», SciPost Physics Core 6 4, 081 (2023).

[2] Кевин Слэгл, «Квантовые калибровочные сети: новый вид тензорной сети», Квант 7, 1113 (2023).

Приведенные цитаты из САО / НАСА ADS (последнее обновление успешно 2024-03-22 22:55:39). Список может быть неполным, поскольку не все издатели предоставляют подходящие и полные данные о цитировании.

On Цитируемый сервис Crossref Данные о цитировании работ не найдены (последняя попытка 2024-03-22 22:55:38).

Эта статья опубликована в Quantum под Creative Commons Attribution 4.0 International (CC BY 4.0) лицензия. Авторское право остается за первоначальными правообладателями, такими как авторы или их учреждения.

Отметка времени:

Больше от Квантовый журнал