Zapis Big O in analiza algoritmov s primeri Pythona

Predstavitev

Običajno obstaja več načinov za rešitev težave z uporabo računalniškega programa. Na primer, obstaja več načinov za razvrščanje elementov v matriki – lahko uporabite spajanje, razvrščanje mehurčkov, vrsta vstavljanja, in tako naprej. Vsi ti algoritmi imajo svoje prednosti in slabosti in naloga razvijalca je, da jih pretehta, da lahko izbere najboljši algoritem za uporabo v katerem koli primeru uporabe. Z drugimi besedami, glavno vprašanje je, kateri algoritem uporabiti za rešitev specifičnega problema, ko obstaja več rešitev za problem.

Analiza algoritmov se nanaša na analizo kompleksnosti različnih algoritmov in iskanje najučinkovitejšega algoritma za rešitev obravnavanega problema. Zapis Big-O je statistična mera, ki se uporablja za opis kompleksnosti algoritma.

V tem vodniku bomo najprej naredili kratek pregled analize algoritmov in si nato podrobneje ogledali zapis Big-O. Videli bomo, kako lahko uporabimo zapis Big-O za iskanje kompleksnosti algoritmov s pomočjo različnih funkcij Pythona.

Zakaj je analiza algoritmov pomembna?

Da bi razumeli, zakaj je analiza algoritma pomembna, si bomo pomagali s preprostim primerom. Recimo, da vodja da nalogo dvema svojima zaposlenima, naj oblikujejo algoritem v Pythonu, ki izračuna faktoriel števila, ki ga vnese uporabnik. Algoritem, ki ga je razvil prvi zaposleni, izgleda takole:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Upoštevajte, da algoritem preprosto vzame celo število kot argument. Znotraj fact() funkcija spremenljivke z imenom product se inicializira na 1. Zanka se izvaja iz 1 do n in med vsako ponovitvijo vrednost v product se pomnoži s številom, ki ga ponavlja zanka, in rezultat se shrani v product spet spremenljivka. Ko se zanka izvede, se product spremenljivka bo vsebovala faktorial.

Podobno je tudi drugi zaposleni razvil algoritem, ki izračuna faktorijel števila. Drugi zaposleni je uporabil rekurzivno funkcijo za izračun faktoriala števila n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Vodja se mora odločiti, kateri algoritem bo uporabil. Da bi to naredili, so se odločili izbrati, kateri algoritem deluje hitreje. Eden od načinov za to je iskanje časa, potrebnega za izvedbo kode na istem vnosu.

V zvezku Jupyter lahko uporabite %timeit literal, ki mu sledi klic funkcije, da ugotovite čas, ki ga funkcija porabi za izvedbo:

%timeit fact(50)

To nam bo dalo:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Izhod pravi, da algoritem traja 9 mikrosekund (plus/minus 45 nanosekund) na zanko.

Podobno lahko izračunamo, koliko časa potrebuje drugi pristop za izvedbo:

%timeit fact2(50)

Posledica tega bo:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Drugi algoritem vključuje rekurzijo 15 mikrosekund (plus/minus 427 nanosekund).

Čas izvajanja kaže, da je prvi algoritem hitrejši v primerjavi z drugim algoritmom, ki vključuje rekurzijo. Pri velikih vložkih lahko razlika v zmogljivosti postane občutnejša.

Vendar pa čas izvajanja ni dobra metrika za merjenje kompleksnosti algoritma, saj je odvisen od strojne opreme. Za algoritem je potrebna bolj objektivna metrika analize kompleksnosti. Tukaj je Zapis velikega O pride igrati.

Analiza algoritmov z zapisom Big-O

Zapis Big-O označuje razmerje med vhodom v algoritem in koraki, potrebnimi za izvedbo algoritma. Označen je z velikim »O«, ki mu sledita začetni in zaključni oklepaj. Znotraj oklepaja je razmerje med vnosom in koraki, ki jih izvede algoritem, predstavljeno z »n«.

Ključni zaključek je – Big-O ne zanima a zlasti primer, v katerem zaženete algoritem, kot je npr fact(50), temveč, kako dobro deluje Lestvica ob povečanem vložku. To je veliko boljša metrika za ocenjevanje kot konkreten čas za konkreten primer!

Na primer, če obstaja linearno razmerje med vhodom in korakom, ki ga izvede algoritem za dokončanje svoje izvedbe, bo uporabljena notacija Big-O O (n). Podobno je zapis Big-O za kvadratne funkcije is O(n²).

Za izgradnjo intuicije:

• O (n): ob n=1, narejen je 1 korak. pri n=10, narejenih je 10 korakov.
• O(n²): ob n=1, narejen je 1 korak. pri n=10, narejenih je 100 korakov.

At n=1, ta dva bi delovala enako! To je še en razlog, zakaj je opazovanje razmerja med vnosom in številom korakov za obdelavo tega vnosa boljše kot le vrednotenje funkcij z nekim konkretnim vnosom.

Sledi nekaj najpogostejših funkcij Big-O:

Ime	Veliki O
stalna	O (c)
linearno	O (n)
Kvadratno	O(n²)
kubični	O(n³)
Eksponentna	O(2ⁿ)
Logaritmično	O (log (n))
Dnevnik linearni	O(nlog(n))

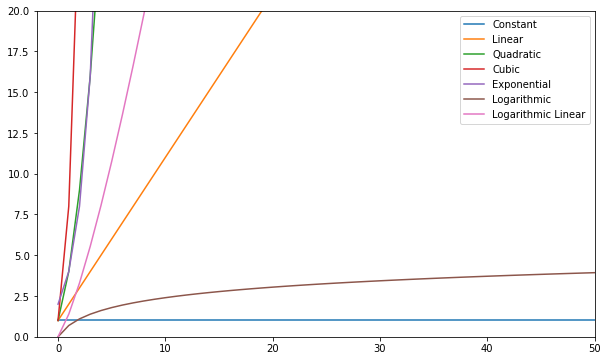
Te funkcije si lahko vizualizirate in jih primerjate:

Na splošno – vse, kar je slabše od linearnega, velja za slabo zapleteno (tj. neučinkovito) in se mu je treba izogibati, če je le mogoče. Linearna kompleksnost je v redu in običajno nujno zlo. Logaritmično je dobro. Konstanta je neverjetna!

Da bi dobili predstavo o tem, kako se izračuna Big-O, si oglejmo nekaj primerov konstantne, linearne in kvadratne kompleksnosti.

Stalna kompleksnost – O(C)

Za kompleksnost algoritma pravimo, da je konstantna, če koraki, potrebni za dokončanje izvedbe algoritma, ostanejo konstantni, ne glede na število vnosov. Konstantna kompleksnost je označena z O (c) Kje c je lahko poljubno konstantno število.

Napišimo preprost algoritem v Pythonu, ki najde kvadrat prvega elementa na seznamu in ga nato natisne na zaslon:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

V zgornjem scenariju ne glede na velikost vnosaali število elementov na vnosnem seznamu items, algoritem izvede samo 2 koraka:

1. Iskanje kvadrata prvega elementa
2. Tiskanje rezultata na zaslon.

Zato kompleksnost ostaja konstantna.

Če narišete črto z različno velikostjo items vnesite na os X in število korakov na os Y, boste dobili ravno črto. Ustvarimo kratek skript, ki nam bo pomagal to vizualizirati. Ne glede na število vnosov ostaja število izvedenih korakov enako:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

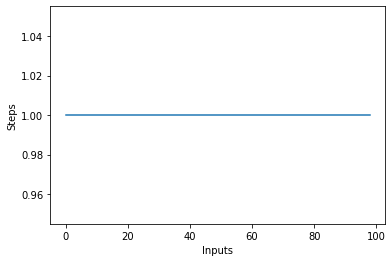
Linearna kompleksnost – O (n)

Za kompleksnost algoritma pravimo, da je linearna, če se koraki, potrebni za dokončanje izvedbe algoritma, linearno povečujejo ali zmanjšujejo s številom vhodov. Linearna kompleksnost je označena z O (n).

V tem primeru napišimo preprost program, ki na konzoli prikaže vse elemente na seznamu:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Kompleksnost linear_algo() funkcija je v zgornjem primeru linearna, saj bo število ponovitev zanke for enako enaka velikosti vnosa items matrika. Na primer, če so v items seznam, bo zanka for izvedena 4-krat.

Na hitro ustvarimo graf za algoritem linearne kompleksnosti s številom vnosov na osi x in številom korakov na osi y:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Posledica tega bo:

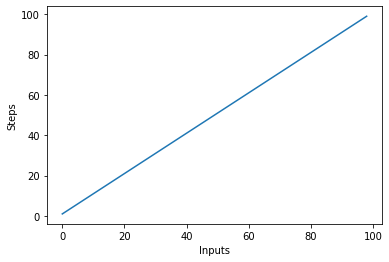
Pomembno je omeniti, da pri velikih vnosih konstante ponavadi izgubijo vrednost. Zato običajno odstranimo konstante iz zapisa Big-O in izraz, kot je O(2n), običajno skrajšamo na O(n). Tako O(2n) kot O(n) sta linearna – pomembno je linearno razmerje, ne konkretna vrednost. Na primer, spremenimo linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Obstajata dve for-zanki, ki ponavljata vnos items seznam. Zato postane kompleksnost algoritma O (2n), vendar je v primeru neskončnega števila postavk na vhodnem seznamu dvakratnik neskončnosti še vedno enak neskončnosti. Konstanto lahko zanemarimo 2 (ker je na koncu nepomemben) in kompleksnost algoritma ostaja O (n).

Predstavimo si ta novi algoritem tako, da narišemo vnose na os X in število korakov na os Y:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

V zgornjem scenariju lahko to jasno vidite y=2nvendar je rezultat linearen in izgleda takole:

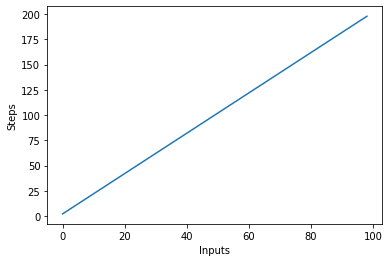
Kvadratna kompleksnost – O(n²)

Za kompleksnost algoritma pravimo, da je kvadratna, če so koraki, potrebni za izvedbo algoritma, kvadratna funkcija števila elementov v vhodu. Kvadratna kompleksnost je označena kot O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Imamo zunanjo zanko, ki ponovi vse elemente na vhodnem seznamu, nato pa ugnezdeno notranjo zanko, ki ponovno pregleda vse elemente na vhodnem seznamu. Skupno število izvedenih korakov je n*n, kjer je n število elementov v vhodni matriki.

Naslednji graf prikazuje število vnosov glede na korake za algoritem s kvadratno kompleksnostjo:

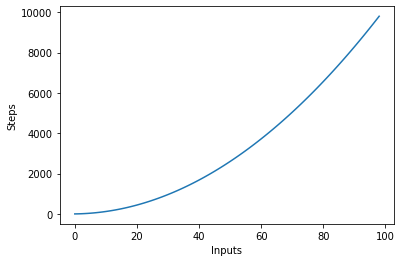
Logaritemska kompleksnost – O (prijava)

Nekateri algoritmi dosegajo logaritemsko kompleksnost, kot npr Binarno iskanje. Binarno iskanje išče element v matriki tako, da označi srednji matrike in obrezovanje polovice, v kateri element ni. To stori znova za preostalo polovico in nadaljuje iste korake, dokler elementa ne najde. V vsakem koraku je polovice število elementov v nizu.

To zahteva, da je matrika razvrščena in da lahko predpostavimo podatke (na primer, da so razvrščeni).

Ko lahko naredite predpostavke o vhodnih podatkih, lahko naredite korake, ki zmanjšajo kompleksnost algoritma. Logaritemska zapletenost je zaželena, saj dosega dobro zmogljivost tudi z visoko skaliranim vnosom.

Iskanje kompleksnosti kompleksnih funkcij?

V prejšnjih primerih smo imeli pri vnosu dokaj preproste funkcije. Kako pa izračunamo Big-O funkcij, ki kličejo (več) drugih funkcij na vhodu?

Oglejmo si:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

V zgornjem skriptu se izvaja več nalog, najprej se na konzoli 5-krat natisne niz z uporabo print izjava. Nato na zaslon dvakrat natisnemo seznam vnosov in na koncu se na konzoli trikrat natisne še en niz. Da bi našli kompleksnost takšnega algoritma, moramo kodo algoritma razdeliti na dele in poskusiti najti kompleksnost posameznih delov. Označite kompleksnost vsakega dela.

V prvem delu imamo:

for i in range(5):
	print("Python is awesome")

Kompleksnost tega dela je O (5) ker se v tem delu kode izvaja pet konstantnih korakov ne glede na vnos.

Nato imamo:

for item in items:
	print(item)

Vemo, da je zgornji del kode zapleten O (n). Podobno je zapletenost naslednjega dela kode O (n):

for item in items:
	print(item)

Končno je v naslednjem delu kode niz natisnjen trikrat, zato je zapletenost O (3):

print("Big O")
print("Big O")
print("Big O")

Da bi našli celotno kompleksnost, moramo preprosto dodati te posamezne kompleksnosti:

O(5) + O(n) + O(n) + O(3)

Če poenostavimo zgoraj, dobimo:

O(8) + O(2n) = O(8+2n)

Prej smo rekli, da ko vhod (ki ima v tem primeru dolžino n) postane izjemno velik, postanejo konstante nepomembne, tj. dvakrat ali polovica neskončnosti še vedno ostane neskončnost. Zato lahko konstante zanemarimo. Končna kompleksnost algoritma bo O (n)!

Kompleksnost najslabšega v primerjavi z najboljšim primerom

Običajno, ko vas nekdo vpraša o kompleksnosti algoritma – ga zanima kompleksnost v najslabšem primeru (Big-O). Včasih jih morda zanima tudi najboljša zapletenost (Big-Omega).

Da bi razumeli razmerje med temi, si poglejmo še en del kode:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

V zgornjem skriptu imamo funkcijo, ki kot vhod sprejme številko in seznam številk. Vrne true, če je posredovano število najdeno na seznamu števil, sicer vrne None. Če iščete 2 na seznamu, ga boste našli v prvi primerjavi. To je najboljši primer zapletenosti algoritma, saj je iskani element najden v prvem iskanem indeksu. Najboljša zapletenost primera, v tem primeru je O (1). Po drugi strani pa, če iščete 10, ga boste našli pri zadnjem iskanem indeksu. Algoritem bo torej moral iskati po vseh elementih na seznamu kompleksnost v najslabšem primeru postane O (n).

Poleg najboljše in najslabše zapletenosti lahko tudi izračunate povprečna kompleksnost (Big-Theta) algoritma, ki vam pove "kakšna je pričakovana časovna kompleksnost algoritma glede na naključni vnos"?

Zapletenost prostora

Poleg časovne kompleksnosti, kjer štejete število korakov, potrebnih za dokončanje izvedbe algoritma, lahko najdete tudi kompleksnost prostora ki se nanaša na količino prostora, ki ga morate dodeliti v pomnilniku med izvajanjem programa.

Oglejte si naslednji primer:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

O return_squares() funkcija sprejme seznam celih števil in vrne seznam z ustreznimi kvadratki. Algoritem mora dodeliti pomnilnik za enako število elementov kot na vhodnem seznamu. Zato postane prostorska kompleksnost algoritma O (n).

zaključek

Zapis Big-O je standardna metrika, ki se uporablja za merjenje kompleksnosti algoritma. V tem priročniku smo preučevali, kaj je zapis Big-O in kako ga je mogoče uporabiti za merjenje kompleksnosti različnih algoritmov. Preučevali smo tudi različne vrste funkcij Big-O s pomočjo različnih primerov Python. Na koncu smo na kratko pregledali najslabšo in najboljšo zahtevnost primera skupaj s kompleksnostjo prostora.