Dokončni vodnik za združevanje v gruče K-Means s Scikit-Learn

Predstavitev

K-pomeni grozd je eden najbolj razširjenih algoritmov nenadzorovanega strojnega učenja, ki tvorijo skupine podatkov na podlagi podobnosti med primerki podatkov.

V tem priročniku si bomo najprej ogledali preprost primer, da bi razumeli, kako deluje algoritem K-Means, preden ga implementiramo s pomočjo Scikit-Learn. Nato bomo razpravljali o tem, kako določiti število grozdov (Ks) v K-Means, in obravnavali tudi metriko razdalje, varianco ter prednosti in slabosti K-Means.

Motivacija

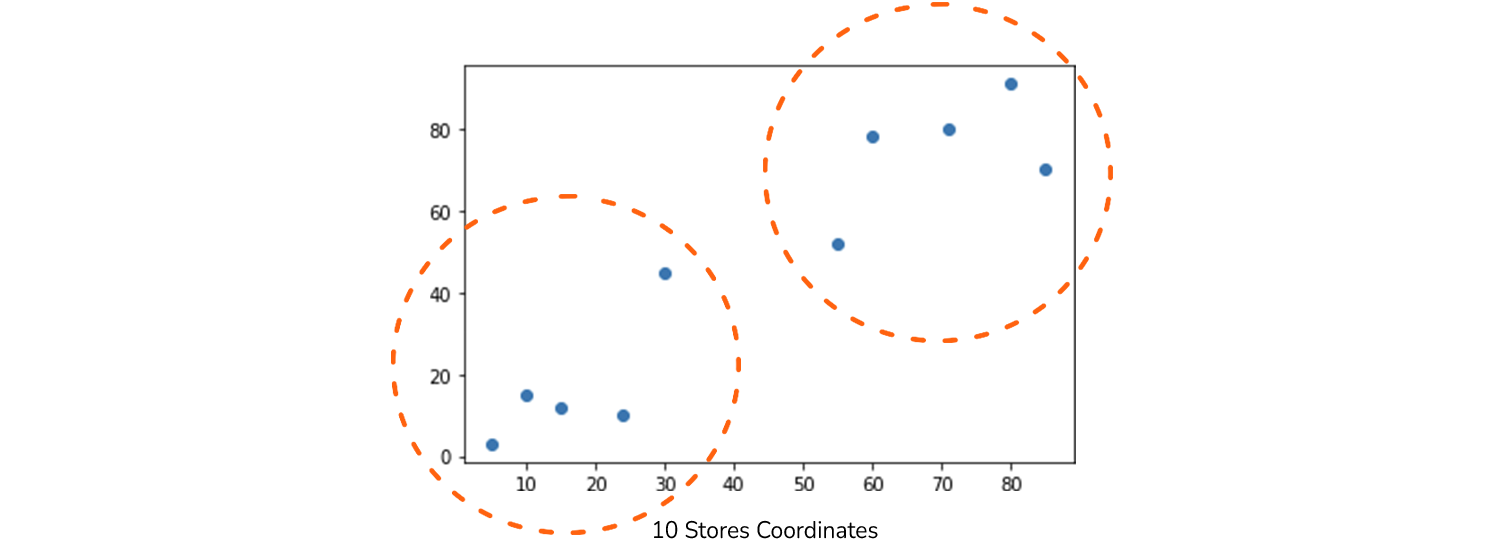
Predstavljajte si naslednjo situacijo. Ko ste se nekega dne sprehajali po soseski, ste opazili, da je 10 trgovin z mešanim blagom, in začeli ste se spraševati, katere trgovine so si podobne – bližje ena drugi v bližini. Med iskanjem odgovora na to vprašanje ste naleteli na zanimiv pristop, ki razdeli trgovine v skupine glede na njihove koordinate na zemljevidu.

Na primer, če bi bila ena trgovina 5 km zahodno in 3 km severno – bi dodelili (5, 3) koordinate nanjo in jo predstavite v grafu. Narišimo to prvo točko, da si predstavljamo, kaj se dogaja:

import matplotlib.pyplot as plt

plt.title("Store With Coordinates (5, 3)")
plt.scatter(x=5, y=3)

To je le prva točka, da lahko dobimo predstavo o tem, kako lahko predstavljamo trgovino. Recimo, da že imamo 10 koordinat za 10 zbranih trgovin. Potem ko jih je organiziral v a numpy niz, lahko narišemo tudi njihove lokacije:

import numpy as np

points = np.array([[5, 3], [10, 15], [15, 12], [24, 10], [30, 45], [85, 70], [71, 80], [60, 78], [55, 52],[80, 91]])

xs = points[:,0] 
ys = points[:,1]  

plt.title("10 Stores Coordinates")
plt.scatter(x=xs, y=ys)

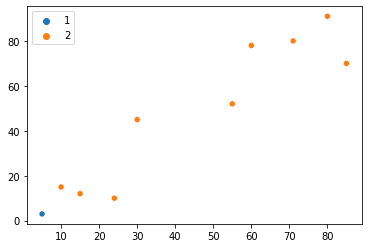
Kako ročno implementirati algoritem K-Means

Zdaj lahko pogledamo 10 trgovin na grafu in glavna težava je ugotoviti, ali obstaja način, da bi jih lahko razdelili v različne skupine glede na bližino? Če le na hitro pogledamo graf, bomo verjetno opazili dve skupini trgovin – ena je spodnja točka levo spodaj, druga pa zgornje desne točke. Morda lahko celo ločimo tisti dve točki na sredini kot ločeno skupino – torej ustvarjanje tri različne skupine.

V tem razdelku bomo preučili postopek ročnega združevanja točk v skupine – razdelitev v dano število skupin. Tako bomo v bistvu skrbno pregledali vse korake Algoritem združevanja v skupine K-Means. Do konca tega razdelka boste pridobili intuitivno in praktično razumevanje vseh korakov, izvedenih med združevanjem v gruče K-Means. Po tem ga bomo prenesli na Scikit-Learn.

Kako bi bilo najbolje ugotoviti, ali obstajajo dve ali tri skupine točk? Eden preprostih načinov bi bil preprosto izbrati eno število skupin – na primer dve – in nato poskusiti združiti točke na podlagi te izbire.

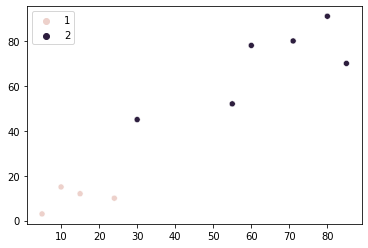
Recimo, da smo se odločili, da obstajajo dve skupini naših poslovalnic (točke). Zdaj moramo najti način, kako razumeti, katere točke pripadajo kateri skupini. To lahko storite tako, da izberete eno točko, ki jo predstavljate skupina 1 in enega za zastopanje skupina 2. Te točke bodo uporabljene kot referenca pri merjenju razdalje od vseh drugih točk do vsake skupine.

Na ta način povejte točko (5, 3) na koncu pripada skupini 1 in točka (79, 60) skupini 2. Pri poskusu dodelitve nove točke (6, 3) skupinam, moramo izmeriti njegovo razdaljo do teh dveh točk. V primeru točke (6, 3) is bližje k (5, 3), zato spada v skupino, ki jo predstavlja ta točka – skupina 1. Tako zlahka združimo vse točke v ustrezne skupine.

V tem primeru poleg določanja števila skupin (grozdi) – izbiramo tudi nekaj točk, ki bodo a reference razdalje za nove točke vsake skupine.

To je splošna ideja za razumevanje podobnosti med našimi trgovinami. Uporabimo to v praksi – najprej lahko izberemo dve referenčni točki pri naključno. Referenčna točka za skupina 1 bo (5, 3) in referenčno točko skupina 2 bo (10, 15). Izberemo lahko obe točki numpy niz po [0] in [1] indekse in jih shranite g1 (skupina 1) in g2 (skupina 2) spremenljivke:

g1 = points[0]
g2 = points[1]

Ko to storimo, moramo izračunati razdaljo od vseh drugih točk do teh referenčnih točk. To postavlja pomembno vprašanje - kako izmeriti to razdaljo. V bistvu lahko uporabimo katero koli mero razdalje, vendar za namen tega vodnika uporabimo evklidsko razdaljo_.

Koristno je vedeti, da evklidska mera razdalje temelji na Pitagorovem izreku:

$$
c^2 = a^2 + b^2
$$

Pri prilagajanju točkam v ravnini – (a1, b1) in (a2, b2)prejšnja formula postane:

$$
c^2 = (a2-a1)^2 + (b2-b1)^2
$$

Razdalja bo kvadratni koren iz c, zato lahko formulo zapišemo tudi kot:

$$
evklidska_{dist} = sqrt[2][(a2 – a1)^2 + (b2 – b1) ^2)]
$$

Doslej smo izbrali točke, ki predstavljajo skupine, in znamo izračunati razdalje. Zdaj pa združimo razdalje in skupine tako, da vsako od naših zbranih trgovinskih točk dodelimo skupini.

Da bi si to bolje predstavljali, bomo razglasili tri sezname. Prvi shrani točke prve skupine – points_in_g1. Drugi za shranjevanje točk iz skupine 2 – points_in_g2, zadnji pa – group, Da nalepka točke kot bodisi 1 (spada v skupino 1) oz 2 (spada v skupino 2):

points_in_g1 = []
points_in_g2 = []
group = []

Zdaj lahko ponavljamo naše točke in izračunamo evklidsko razdaljo med njimi in vsako od referenc naše skupine. Vsaka točka bo bližje v eno od dveh skupin – glede na to, kateri skupini je najbližje, bomo vsako točko dodelili pripadajočemu seznamu, pri tem pa dodali 1 or 2 k group seznam:

for p in points:
    x1, y1 = p[0], p[1]
    euclidean_distance_g1 = np.sqrt((g1[0] - x1)**2 + (g1[1] - y1)**2)
    euclidean_distance_g2 = np.sqrt((g2[0] - x1)**2 + (g2[1] - y1)**2)
    if euclidean_distance_g1 < euclidean_distance_g2:
        points_in_g1.append(p)
        group.append('1')
    else:
        points_in_g2.append(p)
        group.append('2')

Poglejmo rezultate te ponovitve, da vidimo, kaj se je zgodilo:

print(f'points_in_g1:{points_in_g1}n 
npoints_in_g2:{points_in_g2}n 
ngroup:{group}')

Posledica tega je:

points_in_g1:[array([5, 3])]
 
points_in_g2:[array([10, 15]), array([15, 12]), 
              array([24, 10]), array([30, 45]), 
              array([85, 70]), array([71, 80]),
              array([60, 78]), array([55, 52]), 
              array([80, 91])]
 
group:[1, 2, 2, 2, 2, 2, 2, 2, 2, 2] 

Rezultat gručenja lahko narišemo tudi z različnimi barvami glede na dodeljene skupine, z uporabo Seabornovega scatterplot() s group kot hue argument:

import seaborn as sns

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

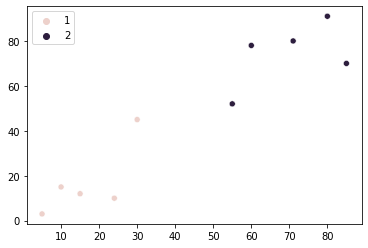
Jasno je razvidno, da je samo naša prva točka dodeljena skupini 1, vse ostale točke pa so bile dodeljene skupini 2. Ta rezultat se razlikuje od tistega, kar smo si zamislili na začetku. Glede na razliko med našimi rezultati in našimi začetnimi pričakovanji – ali obstaja način, da bi to spremenili? Zdi se, da obstaja!

Eden od pristopov je ponoviti postopek in izbrati različne točke za reference skupin. To bo spremenilo naše rezultate, upamo, da bodo bolj v skladu s tem, kar smo si zamislili na začetku. Tokrat jih lahko drugič ne izberemo naključno, kot smo to počeli prej, ampak tako, da dobimo pomeni vseh naših že združenih točk. Tako bi lahko te nove točke postavili na sredino ustreznih skupin.

Na primer, če bi druga skupina imela samo točke (10, 15), (30, 45). Nova Osrednji bistvo bi bilo (10 + 30)/2 in (15+45)/2 – kar je enako (20, 30).

Ker smo svoje rezultate uvrstili na sezname, jih lahko najprej pretvorimo v numpy polja, izberite njihove xs, ys in nato pridobite pomeni:

g1_center = [np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()]
g2_center = [np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()]
g1_center, g2_center

Za pomoč pri ponovitvi postopka z našimi novimi središčnimi točkami preoblikujemo našo prejšnjo kodo v funkcijo, jo izvedimo in preverimo, ali je prišlo do kakršnih koli sprememb v tem, kako so točke razvrščene:

def assigns_points_to_two_groups(g1_center, g2_center):
    points_in_g1 = []
    points_in_g2 = []
    group = []

    for p in points:
        x1, y1 = p[0], p[1]
        euclidean_distance_g1 = np.sqrt((g1_center[0] - x1)**2 + (g1_center[1] - y1)**2)
        euclidean_distance_g2 = np.sqrt((g2_center[0] - x1)**2 + (g2_center[1] - y1)**2)
        if euclidean_distance_g1 < euclidean_distance_g2:
            points_in_g1.append(p)
            group.append(1)
        else:
            points_in_g2.append(p)
            group.append(2)
    return points_in_g1, points_in_g2, group

Pokličimo funkcijo in shranimo njene rezultate points_in_g1, points_in_g2in group spremenljivke:

points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
points_in_g1, points_in_g2, group

Narišite tudi raztreseni grafikon z barvnimi točkami, da vizualizirate delitev skupin:

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

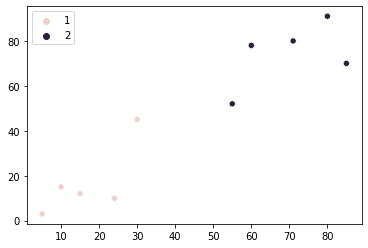
Zdi se, da je združevanje naših točk izboljšanje. Kljub temu sta na sredini grafa dve točki, ki ju je mogoče pripisati kateri koli skupini, če upoštevamo njuno bližino obema skupinama. Algoritem, ki smo ga razvili do sedaj, dodeli obe točki drugi skupini.

To pomeni, da lahko postopek verjetno še enkrat ponovimo, tako da vzamemo srednja mesta Xs in Ys ter ustvarimo dve novi osrednji točki (centroidi) našim skupinam in jih prerazporedimo glede na razdaljo.

Ustvarimo tudi funkcijo za posodobitev centroidov. Celoten postopek je zdaj mogoče zmanjšati na večkratne klice te funkcije:

def updates_centroids(points_in_g1, points_in_g2):
    g1_center = np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()
    g2_center = np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()
    return g1_center, g2_center

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

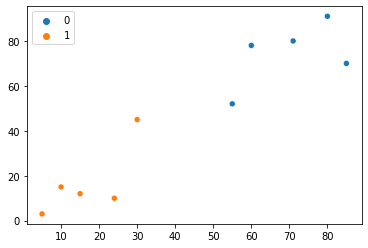
Upoštevajte, da po tej tretji ponovitvi vsaka od točk zdaj pripada različnim grozdom. Zdi se, da se rezultati izboljšujejo – ponovimo. Zdaj grem na četrta ponovitev naše metode:

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

To četrtič smo dobili enak rezultat kot prejšnji. Tako se zdi, da naše točke ne bodo več spreminjale skupin, naš rezultat je dosegel nekakšno stabilnost – prišel je v nespremenljivo stanje oz. konvergenčne. Poleg tega imamo popolnoma enak rezultat, kot smo si ga zamislili za 2 skupini. Vidimo lahko tudi, ali je ta dosežena delitev smiselna.

Naj na hitro povzamemo, kaj smo naredili do zdaj. Naših 10 trgovin smo geografsko razdelili na dva dela – enega v nižjih jugozahodnih regijah in drugega na severovzhodu. Zanimivo je lahko zbrati več podatkov poleg tistih, ki jih že imamo – prihodek, dnevno število strank in še veliko več. Tako lahko izvedemo bogatejšo analizo in po možnosti ustvarimo bolj zanimive rezultate.

Študije grozdenja, kot je ta, se lahko izvedejo, ko že uveljavljena blagovna znamka želi izbrati območje za odprtje nove trgovine. V tem primeru je poleg lokacije upoštevanih še veliko več spremenljivk.

Kaj ima vse to opraviti z algoritmom K-Means?

Med sledenjem tem korakom ste se morda spraševali, kakšno zvezo imajo z algoritmom K-Means. Postopek, ki smo ga izvedli do sedaj, je Algoritem K-Means. Skratka, določili smo število skupin/gruč, naključno izbrali začetne točke in posodobili centroide v vsaki iteraciji, dokler se grozdi niso zbližali. Celoten algoritem smo v bistvu izvedli ročno – s skrbnim izvajanjem vsakega koraka.

O K v K-Means izvira iz število grozdov ki jih je treba nastaviti pred začetkom postopka ponovitve. V našem primeru K = 2. Ta lastnost se včasih obravnava kot negativna glede na to, da obstajajo druge metode združevanja v gruče, kot je hierarhično združevanje v gruče, za katere ni treba imeti vnaprej določenega števila gruč.

Zaradi svoje uporabe sredstev postane tudi K-sredstvo občutljiv na izstopajoče in ekstremne vrednosti – povečajo variabilnost in otežijo našim centroidom, da odigrajo svojo vlogo. Torej, zavedajte se potrebe po izvedbi analiza ekstremnih vrednosti in odstopanj preden izvedete združevanje v gruče z uporabo algoritma K-Means.

Upoštevajte tudi, da so bile naše točke segmentirane v ravnih delih, pri ustvarjanju grozdov ni krivulj. To je lahko tudi pomanjkljivost algoritma K-Means.

Veliko jih ima tudi K-Means Prednosti! Dobro se obnese na Velikih podatkovnih nizov kar lahko postane težko obvladljivo, če uporabljate nekatere vrste hierarhičnih algoritmov za združevanje v gruče. Tudi zagotavlja konvergenco, in lahko enostavno posplošiti in prilagodijo. Poleg tega je verjetno najpogosteje uporabljen algoritem združevanja v gruče.

Zdaj, ko smo pregledali vse korake, izvedene v algoritmu K-Means, in razumeli vse njegove prednosti in slabosti, lahko končno implementiramo K-Means s knjižnico Scikit-Learn.

Kako implementirati algoritem K-Means z uporabo scikit-learn

Če želite dvakrat preveriti naš rezultat, ponovimo ta postopek, vendar zdaj z uporabo 3 vrstic kode z sklearn:

from sklearn.cluster import KMeans


kmeans = KMeans(n_clusters=2, random_state=42) 
kmeans.fit(points)
kmeans.labels_

Tukaj so oznake enake našim prejšnjim skupinam. Na hitro narišite rezultat:

sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Nastala ploskev je enaka tisti iz prejšnjega razdelka.

S Scikit-Learn lahko tudi inicializirate K-Means za hitrejšo konvergenco tako, da nastavite init='k-means++' prepir. V širšem smislu, K-pomeni++ še vedno izbere k začetni centri grozdov naključni po enotni porazdelitvi. Nato je vsako naslednje središče gruče izbrano izmed preostalih podatkovnih točk ne z izračunom le mere razdalje – ampak z uporabo verjetnosti. Uporaba verjetnosti pospeši algoritem in je koristna pri delu z zelo velikimi nabori podatkov.

Metoda komolca – izbira najboljšega števila skupin

Zaenkrat gre dobro! Združili smo 10 trgovin na podlagi evklidske razdalje med točkami in centroidi. Kaj pa tisti dve točki na sredini grafa, ki ju je malo težje združiti? Ali ne bi mogli tudi oni oblikovati ločene skupine? Ali smo se z izbiro dejansko zmotili K = 2 skupine? Mogoče smo res imeli K = 3 skupine? Lahko bi imeli celo več kot tri skupine in se tega ne bi zavedali.

Tukaj se postavlja vprašanje kako določiti število skupin (K) v K-Means. Da bi odgovorili na to vprašanje, moramo razumeti, ali bi obstajal "boljši" grozd za drugačno vrednost K.

Naiven način, da to ugotovimo, je z združevanjem točk z različnimi vrednostmi K, torej, za K=2, K=3, K=4 in tako naprej:

for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 

Toda združevanje točk za različne Ks sam ne bo dovolj da razumemo, ali smo izbrali idealno vrednost za K. Potrebujemo način za ovrednotenje kakovosti grozdenja za vsakega K smo izbrali.

Ročno izračunavanje Vsota kvadratov gruče (WCSS)

Tukaj je idealno mesto za uvedbo merila, koliko so naše gručaste točke blizu druga drugi. V bistvu opisuje, koliko variance imamo znotraj ene same gruče. Ta ukrep se imenuje Znotraj grozda Vsota kvadratovali WCSS na kratko. Manjši kot je WCSS, bližje so naše točke, zato imamo bolj oblikovan grozd. Formulo WCSS je mogoče uporabiti za poljubno število grozdov:

$$
WCSS = vsota (Pi_1 – Centroid_1)^2 + cdots + vsota (Pi_n – Centroid_n)^2
$$

Zdaj lahko domnevamo, da smo se odločili za dve gruči in poskušali implementirati WCSS, da bi bolje razumeli, kaj je WCSS in kako ga uporabljati. Kot navaja formula, moramo sešteti kvadratne razlike med vsemi točkami grozda in centroidi. Torej, če je naša prva točka iz prve skupine (5, 3) in naš zadnji centroid (po konvergenci) prve skupine je (16.8, 17.0), bo WCSS:

$$
WCSS = vsota ((5,3) – (16.8, 17.0))^2
$$

$$
WCSS = vsota((5-16.8) + (3-17.0))^2
$$

$$
WCSS = vsota ((-11.8) + (-14.0))^2
$$

$$
WCSS = vsota((-25.8))^2
$$

$$
WCSS = 335.24
$$

Ta primer ponazarja, kako izračunamo WCSS za eno točko iz gruče. Toda grozd običajno vsebuje več kot eno točko in pri izračunu WCSS jih moramo upoštevati vse. To bomo naredili tako, da definiramo funkcijo, ki prejme skupino točk in centroidov ter vrne vsoto kvadratov:

def sum_of_squares(cluster, centroid):
    squares = []
    for p in cluster:
        squares.append((p - centroid)**2)
        ss = np.array(squares).sum()
    return ss

Zdaj lahko dobimo vsoto kvadratov za vsako gručo:

g1 = sum_of_squares(points_in_g1, g1_center)
g2 = sum_of_squares(points_in_g2, g2_center)

In seštejte rezultate, da dobite skupno WCSS:

g1 + g2

Rezultat tega je:

2964.3999999999996

Torej, v našem primeru, ko K je enak 2, skupni WCSS je 2964.39. Zdaj lahko zamenjamo K in izračunamo WCSS za vse. Tako lahko dobimo vpogled v to, kaj K odločiti se moramo, da bo naše združevanje v gruče delovalo najbolje.

Izračun WCSS Uporaba scikit-learn

Na srečo nam ni treba ročno izračunati WCSS za vsakega K. Po izvedbi združevanja v gruče K-Means za dano število gruč lahko dobimo njegov WCSS z uporabo inertia_ atribut. Zdaj se lahko vrnemo k našemu K-sredstvu for zanke, jo uporabite za preklop števila gruč in seznam ustreznih vrednosti WCSS:

wcss = [] 
for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 
    wcss.append(kmeans.inertia_)
wcss

Upoštevajte, da je druga vrednost na seznamu popolnoma enaka, za katero smo izračunali prej K = 2:

[18272.9, # For k=1 
 2964.3999999999996, # For k=2
 1198.75, # For k=3
 861.75,
 570.5,
 337.5,
 175.83333333333334,
 79.5,
 17.0,
 0.0]

Da bi vizualizirali te rezultate, narišite naše Ks skupaj z vrednostmi WCSS:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
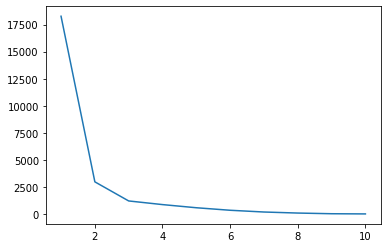
plt.plot(ks, wcss)

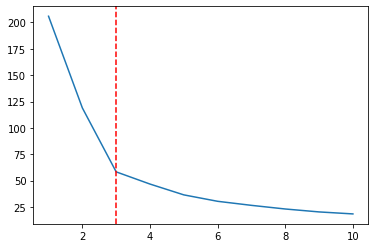
Na parceli pride do prekinitve, ko x = 2, nizko točko v črti, še nižjo pa, ko x = 3. Opazite, da nas spominja na oblika komolca. Z izrisom Ks skupaj z WCSS uporabljamo Metoda komolca izbrati število Ks. In izbrani K je točno najnižja točka komolca, tako bi bilo 3 Namesto 2, v našem primeru:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
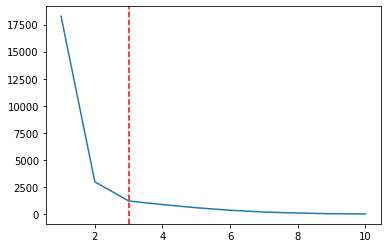
plt.plot(ks, wcss);
plt.axvline(3, linestyle='--', color='r')

Znova lahko zaženemo algoritem gruče K-Means, da vidimo, kako bi bili videti naši podatki trije grozdi:

kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(points)
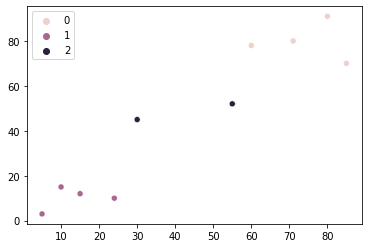
sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Zadovoljni smo bili že z dvema grozdoma, vendar bi po metodi komolca trije grozdi bolje ustrezali našim podatkom. V tem primeru bi namesto dveh imeli tri vrste trgovin. Pred komolčno metodo smo razmišljali o jugozahodnih in severovzhodnih grozdih trgovin, zdaj imamo trgovine tudi v centru. Mogoče bi bila to dobra lokacija za odprtje druge trgovine, saj bi imela v bližini manjšo konkurenco.

Alternativni ukrepi kakovosti grozdov

Obstajajo tudi drugi ukrepi, ki jih je mogoče uporabiti pri ocenjevanju kakovosti grozda:

• Rezultat silhuete – analizira ne le razdaljo med točkami znotraj grozda, ampak tudi med samimi grozdi
• Vsota kvadratov med grozdi (BCSS) – metrika, ki dopolnjuje WCSS
• Napaka vsote kvadratov (ESS)
• Največji radij – meri največjo razdaljo od točke do njenega težišča
• Povprečni radij – vsota največje razdalje od točke do njenega težišča, deljena s številom grozdov.

Priporočljivo je, da eksperimentirate in spoznate vsako od njih, saj so lahko nekatere alternative bolj uporabne kot najbolj razširjene meritve, odvisno od težave. (WCSS in rezultat silhuete).

Na koncu, tako kot pri mnogih algoritmih podatkovne znanosti, želimo zmanjšati varianco znotraj vsake gruče in čim bolj povečati varianco med različnimi grozdi. Tako imamo več definiranih in ločljivih grozdov.

Uporaba K-Means na drugem nizu podatkov

Uporabimo, kar smo se naučili, na drugem nizu podatkov. Tokrat bomo poskušali najti skupine podobnih vin.

Začnemo z uvozom pandas prebrati wine-clustering CSV (Vrednosti, ločene z vejicami) datoteko v a Dataframe zgradba:

import pandas as pd

df = pd.read_csv('wine-clustering.csv')

Ko ga naložimo, pokukajmo v prvih pet zapisov podatkov z head() metoda:

df.head()

Rezultat tega je:

	Alcohol 	Malic_Acid 	Ash 	Ash_Alcanity 	Magnesium 	Total_Phenols 	Flavanoids 	Nonflavanoid_Phenols 	Proanthocyanins 	Color_Intensity 	Hue 	OD280 	Proline
0 	14.23 		1.71 		2.43 	15.6 			127 		2.80 			3.06 		0.28 					2.29 				5.64 				1.04 	3.92 	1065
1 	13.20 		1.78 		2.14 	11.2 			100 		2.65 			2.76 		0.26 					1.28 				4.38 				1.05 	3.40 	1050
2 	13.16 		2.36 		2.67 	18.6 			101 		2.80 			3.24 		0.30 					2.81 				5.68 				1.03 	3.17 	1185
3 	14.37 		1.95 		2.50 	16.8 			113 		3.85 			3.49 		0.24 					2.18 				7.80 				0.86 	3.45 	1480
4 	13.24 		2.59 		2.87 	21.0 			118 		2.80 			2.69 		0.39 					1.82 				4.32 				1.04 	2.93 	735

Imamo veliko meritev snovi, prisotnih v vinih. Tukaj nam prav tako ne bo treba preoblikovati kategoričnih stolpcev, ker so vsi številski. Zdaj pa si oglejmo opisno statistiko z describe() metoda:

df.describe().T 

Tabela opisa:

 						count 	mean 		std 		min 	25% 	50% 	75% 		max
Alcohol 				178.0 	13.000618 	0.811827 	11.03 	12.3625 13.050 	13.6775 	14.83
Malic_Acid 				178.0 	2.336348 	1.117146 	0.74 	1.6025 	1.865 	3.0825 		5.80
Ash 					178.0 	2.366517 	0.274344 	1.36 	2.2100 	2.360 	2.5575 		3.23
Ash_Alcanity 			178.0 	19.494944 	3.339564 	10.60 	17.2000 19.500 	21.5000 	30.00
Magnesium 				178.0 	99.741573 	14.282484 	70.00 	88.0000 98.000 	107.0000 	162.00
Total_Phenols 			178.0 	2.295112 	0.625851 	0.98 	1.7425 	2.355 	2.8000 		3.88
Flavanoids 				178.0 	2.029270 	0.998859 	0.34 	1.2050 	2.135 	2.8750 		5.08
Nonflavanoid_Phenols 	178.0 	0.361854 	0.124453 	0.13 	0.2700 	0.340 	0.4375 		0.66
Proanthocyanins 		178.0 	1.590899 	0.572359 	0.41 	1.2500 	1.555 	1.9500 		3.58
Color_Intensity 		178.0 	5.058090 	2.318286 	1.28 	3.2200 	4.690 	6.2000 		13.00
Hue 					178.0 	0.957449 	0.228572 	0.48 	0.7825 	0.965 	1.1200 		1.71
OD280 					178.0 	2.611685 	0.709990 	1.27 	1.9375 	2.780 	3.1700 		4.00
Proline 				178.0 	746.893258 	314.907474 	278.00 	500.500 673.500 985.0000 	1680.00

Ob pogledu na tabelo je jasno, da jih je nekaj variabilnost podatkov – za nekatere rubrike, kot npr Alchool je več, in za druge, kot npr Malic_Acid, manj. Zdaj lahko preverimo, ali obstajajo nullali NaN vrednosti v našem naboru podatkov:

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 13 columns):
 #   Column                Non-Null Count  Dtype  
---  ------                --------------  -----  
 0   Alcohol               178 non-null    float64
 1   Malic_Acid            178 non-null    float64
 2   Ash                   178 non-null    float64
 3   Ash_Alcanity          178 non-null    float64
 4   Magnesium             178 non-null    int64  
 5   Total_Phenols         178 non-null    float64
 6   Flavanoids            178 non-null    float64
 7   Nonflavanoid_Phenols  178 non-null    float64
 8   Proanthocyanins       178 non-null    float64
 9   Color_Intensity       178 non-null    float64
 10  Hue                   178 non-null    float64
 11  OD280                 178 non-null    float64
 12  Proline               178 non-null    int64  
dtypes: float64(11), int64(2)
memory usage: 18.2 KB

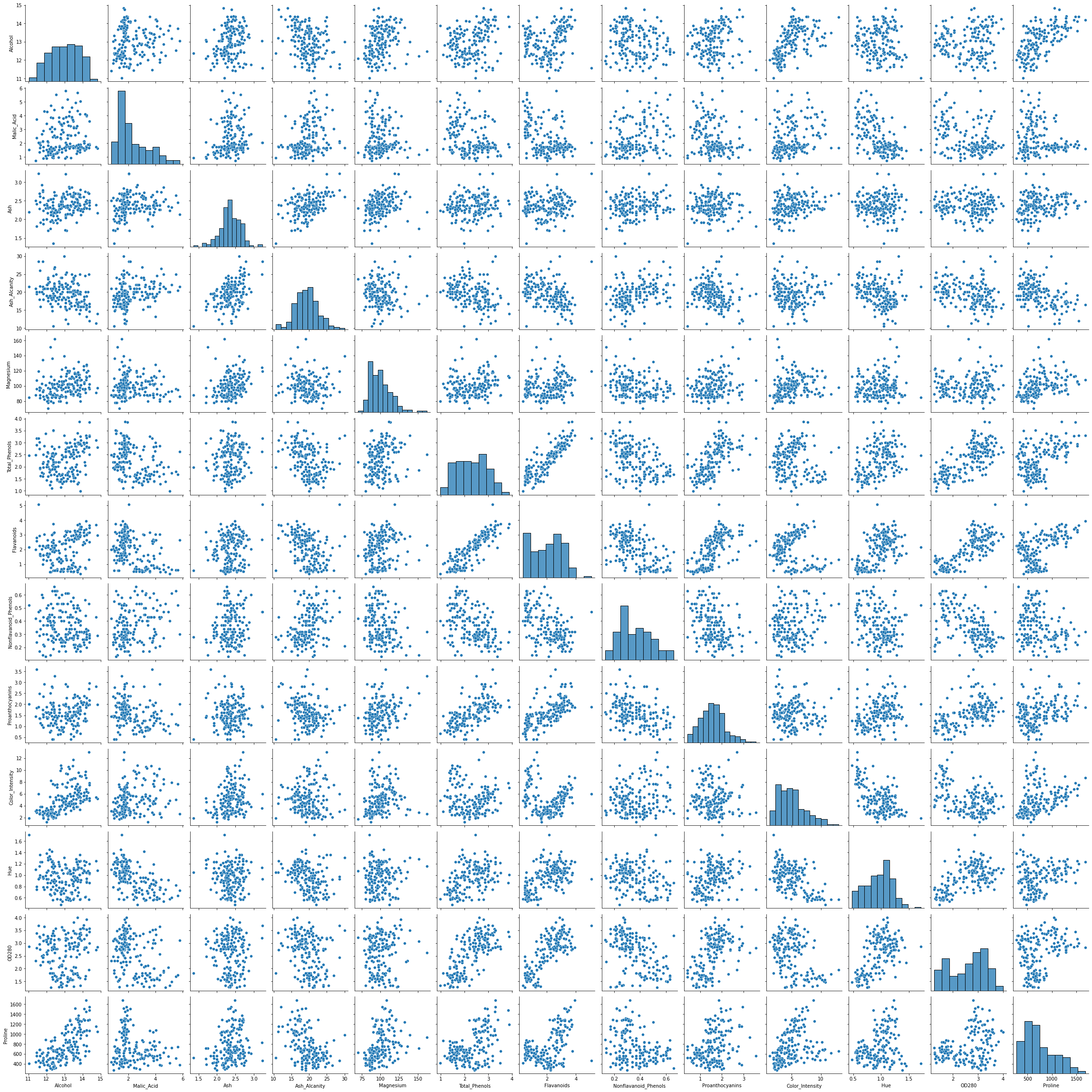
Podatkov ni treba izpuščati ali vnašati, saj v naboru podatkov ni praznih vrednosti. Lahko uporabimo Seaborn pairplot() da vidite porazdelitev podatkov in preverite, ali nabor podatkov tvori pare stolpcev, ki so lahko zanimivi za združevanje v gruče:

sns.pairplot(df)

Če pogledamo parno ploskev, se zdita dva stolpca obetavna za namene združevanja v gruče – Alcohol in OD280 (ki je metoda za določanje koncentracije beljakovin v vinih). Zdi se, da na ploskvah obstajajo 3 ločeni grozdi, ki združujejo dva od njih.

Obstajajo tudi drugi stolpci, za katere se zdi, da so v korelaciji. Predvsem Alcohol in Total_Phenolsin Alcohol in Flavanoids. Imajo odlična linearna razmerja, ki jih je mogoče opaziti na ploskvi v paru.

Ker je naš fokus združevanje v gruče s K-srednjimi vrednostmi, izberimo en par stolpcev, recimo Alcohol in OD280in preizkusite metodo komolca za ta niz podatkov.

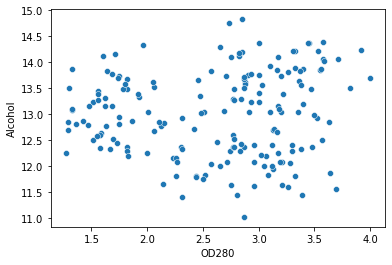
Narišimo razpršeni diagram s tema dvema stolpcema, ki sta nastavljena kot njegova os, da si pobližje ogledamo točke, ki jih želimo razdeliti v skupine:

sns.scatterplot(data=df, x='OD280', y='Alcohol')

Zdaj lahko definiramo naše stolpce in uporabimo metodo komolca za določitev števila grozdov. Algoritem bomo sprožili tudi z kmeans++ samo zato, da se prepričam, da se hitreje združi:

values = df[['OD280', 'Alcohol']]

wcss_wine = [] 
for i in range(1, 11): 
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(values) 
    wcss_wine.append(kmeans.inertia_)

Izračunali smo WCSS, tako da lahko narišemo rezultate:

clusters_wine = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
plt.plot(clusters_wine, wcss_wine)
plt.axvline(3, linestyle='--', color='r')

Po metodi komolcev bi morali imeti tukaj 3 grozde. Za zadnji korak združimo naše točke v 3 skupine in narišite te skupine, označene z barvami:

kmeans_wine = KMeans(n_clusters=3, random_state=42)
kmeans_wine.fit(values)
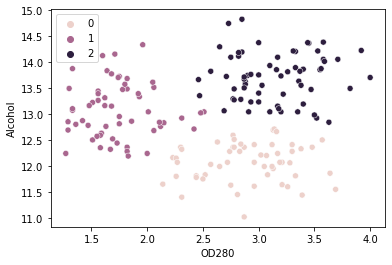
sns.scatterplot(x = values['OD280'], y = values['Alcohol'], hue=kmeans_wine.labels_)

Vidimo lahko grozde 0, 1in 2 v grafu. Na podlagi naše analize, skupina 0 ima vina z višjo vsebnostjo beljakovin in manj alkohola, skupina 1 ima vina z višjo vsebnostjo alkohola in malo beljakovin ter skupina 2 ima v svojih vinih visoko vsebnost beljakovin in alkohola.

To je zelo zanimiv nabor podatkov in spodbujam vas, da greste dlje v analizo z združevanjem podatkov po normalizaciji in PCA – tudi z interpretacijo rezultatov in iskanjem novih povezav.

zaključek

K-Pomeni združevanje v gruče je preprost, a zelo učinkovit nenadzorovan algoritem strojnega učenja za združevanje podatkov v gruče. Podatke združuje v skupine na podlagi evklidske razdalje med podatkovnimi točkami. Algoritem za združevanje v gruče K-Means ima veliko uporab za združevanje besedilnih dokumentov, slik, videoposnetkov in še veliko več.