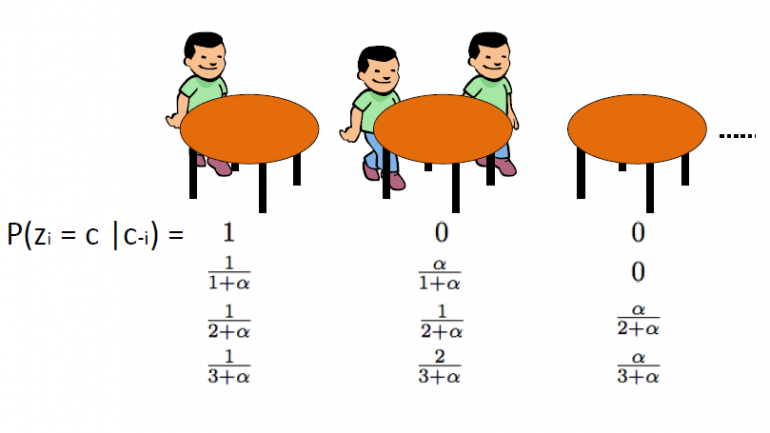Dirichlet obdeluje kitajski restavracijski postopek in druge predstavitve

• Maj 20, 2014
• Vasilis Vryniotis
• . Brez komentarja

Ta članek je tretji del v seriji o grozdu z modeli mešanic procesnih mešanic Dirichlet. Prejšnjič smo definirali model končnih mešanic na podlagi Dirichletove distribucije in postavljali smo vprašanja, kako lahko ta poseben model naredimo neskončen. Na kratko smo razpravljali o zamisli o prevzemu meje modela, kadar se število klastov nagiba v neskončnost, a ker smo poudarili, da obstoj takega predmeta ni nepomemben (z drugimi besedami, kako dejansko "vzamemo mejo modela" ”?). Kot opomnik je razlog, da želimo sprejeti make k neskončno, ker bomo na ta način imeli neparametrični model, ki ne zahteva, da vnaprej določimo skupno število skupin v podatkih.

Posodobitev: Okvir za strojno učenje Datebox je zdaj odprtokoden in brez njega prenesi. Oglejte si paket com.datumbox.framework.machinelearning.clustering in si oglejte izvedbo modelov mešanic Dirichlet Process Mešanice na Javi.

Čeprav je naš cilj zgraditi model, ki bo sposoben izvajati združevanje v naborih podatkov, moramo razpravljati o procesih Dirichlet. Podali bomo tako stroge matematične definicije kot bolj intuitivne razlage DP in razpravljali bomo o načinih konstruiranja postopka. Te konstrukcije / predstavitve je mogoče razumeti kot način za iskanje pojavnosti Dirichletovega procesa v "resničnem življenju".

Kljub temu, da sem poskušal svoje raziskovalno poročilo prilagoditi tako, da bo lažje slediti tem objavam na spletnem dnevniku, je še vedno pomembno, da določimo potrebna matematična orodja in distribucije, preden se lotimo uporabe modelov. Modeli Dirichlet Process so tema aktivnih raziskav, vendar je pred njihovo uporabo potrebno dobro razumeti statistiko in stohastične procese. Druga težava je, da bomo lahko, kot bomo videli v tem članku, Dirichlet procese predstavljali / konstruirali na številne načine. Posledično več akademskih prispevkov uporablja popolnoma drugačne oznake / konvencije in težavo preučuje z različnih vidikov. V tej objavi jih skušam razložiti čim bolj preprosto in uporabim isti zapis. Upajmo, da bodo stvari postale jasnejše z dvema prihajajočima člankoma, ki se osredotočata na definicijo modelov Dirichlet procesa mešanja in na to, kako jih dejansko uporabiti za izvajanje grozdne analize.

1. Opredelitev postopka Dirichlet

Dirichletov postopek v Θ prostoru je stohastičen proces. Gre za porazdelitev verjetnosti na „porazdelitev verjetnosti čez Θ prostor“ in a črpanje iz nje je diskretna porazdelitev. Uradno je Dirichletova distribucija porazdelitev po verjetnostnih ukrepih. A verjetnostni ukrep je funkcija podskupin prostora Θ do [0,1]. G je naključna mera verjetnosti, porazdeljena s DP, označena kot , če za katero koli particijo (A₁,… A_n) prostora Θ imamo to .

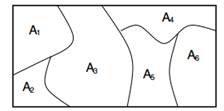
Slika 1: Robovi na končnih particijah so razdeljeni v Dirichletu.

DP ima dva parametra: Prvi je osnovna porazdelitev G₀ ki služi kot sredica . Drugi je trdnostni parameter α, ki je strogo pozitiven in deluje kot obratna varianca . Določa obseg ponovitve vrednosti porazdelitve izhoda. Višja kot je vrednost a, manjša je ponovitev; manjša kot je vrednost, večja je ponovitev vrednosti porazdelitve proizvodnje. Končno je Θ prostor s parametrom, na katerem definiramo DP. Poleg tega je prostor Θ tudi definicijski prostor G₀ ki je enak tistemu iz G.

Preprostejša in več intuitiven način razložiti postopek Dirichleta je naslednje. Predpostavimo, da imamo prostor Θ, ki ga lahko poljubno delimo (A₁,…, A_n) in porazdelitev verjetnosti G, ki jim dodeli verjetnosti. G je specifična porazdelitev verjetnosti nad Θ, vendar obstaja še veliko drugih. Dirichletov postopek na Θ modelih natanko to; gre za porazdelitev na vse možne porazdelitve verjetnosti na prostor Θ. Dirichletov postopek je parametriziran z G₀ osnovna funkcija in parameter koncentracije α. Lahko rečemo, da se G porazdeli glede na DP s parametroma α in G₀ če skupna porazdelitev verjetnosti, ki jih G pripiše particijam Θ, sledi razdelitvi Dirichleta. Lahko pa rečemo, da verjetnosti, ki jih G pripiše kateri koli končni particiji Θ, sledijo Dirichletovi porazdelitvi.

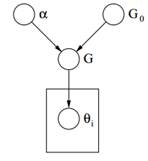
Slika 2: Grafični model Dirichletovega procesa

Končno zgoraj lahko vidimo grafični model DP. Upoštevati moramo, da je α skalarni hiperparameter, G₀ je osnovna porazdelitev DP, G naključna porazdelitev na Θ prostor parametrov, odvzetega iz DP, ki dodeli verjetnosti parametrom in θ_i je vektor parametrov, ki ga črpamo iz porazdelitve G in je element Θ prostora.

2. Posteriorni procesi Dirichlet

O posteriornih procesih Dirichleta je spregovoril Ferguson. Začnemo z risanjem naključne mere verjetnosti G iz Dirichletovega procesa, . Ker je G porazdelitev verjetnosti nad Θ, lahko vzamemo tudi vzorce iz te porazdelitve in potegnemo neodvisne enakovredno porazdeljene vzorce θ₁,…, Θ_n ~ G. Ker so risbe iz Dirichletovega procesa diskretne porazdelitve, jih lahko predstavljamo Kje je kratek zapis za kar je delta funkcija, ki sprejme 1, če in drugje 0. Zanimiv učinek tega je, da je G tako definiran, da obstaja velika verjetnost, da imajo različni vzorci enako vrednost . Kot bomo videli kasneje, to ustvarja učinek grozda, ki ga lahko uporabimo za izvajanje analize grozdov na naboru podatkov.

Z uporabo zgornjih definicij in opažanj želimo oceniti zadnjo stran Dirichletovega procesa glede na vzorce θ. Kljub temu, ker to vemo in z uporabo Bayesovih pravil in povezave med Dirichletom in Multinomialom imamo to in .

Enačba 1: Posteriorni Dirichletov postopek

Ta lastnost je zelo pomembna in jo uporabljajo različni predstavniki DP.

3. Dirichlet predstavitve procesa

V prejšnjih segmentih smo opredelili postopek Dirichlet in predstavili njegov teoretični model. Pomembno vprašanje, na katerega moramo odgovoriti, je, kako vemo, da tak predmet obstaja in kako zmoremo konstruirati in predstavljati Dirichletov postopek.

Prve znake obstoja je dal Ferguson ki je uporabil teorem o doslednosti Kolmogorov, je dal definicijo Dirichletovega procesa in opisal postopek Posterior Dirichlet. Nadaljuje raziskovanje, Blackwell in MacQueen uporabil teorem de Finettija za dokazovanje obstoja take naključne mere verjetnosti in uvedel shemo urna Blackwell-MacQueen, ki izpolnjuje lastnosti Dirichletovega procesa. Leta 1994 Sethuraman zagotovil dodaten preprost in neposreden način izdelave DP z uvedbo konstrukcije za razbijanje palic. Končno je predstavil še eno predstavitev Aldous ki je predstavil kitajski proces restavracij kot učinkovit način konstruiranja Dirichletovega procesa.

Različne predstavitve Dirichletovega procesa so matematično enakovredne, vendar se njihova formulacija razlikuje, saj problem preučujejo z različnih vidikov. Spodaj predstavljamo najpogostejše predstavitve, ki jih najdemo v literaturi, in se osredotočamo na kitajski postopek restavracij, ki zagotavlja preprost in računalniško učinkovit način za gradnjo algoritmov za sklepanje za Dirichlet proces.

3.1 Shema urn Blackwell-MacQueen

Shemo urne Blackwell-MacQueen lahko uporabite za predstavljanje Dirichletovega procesa in jo je uvedel Blackwell in MacQueen. Temelji na shemi Pólya urne, ki jo je mogoče videti kot nasprotni model vzorčenja brez zamenjave. V shemi Pólya urne predpostavljamo, da imamo nepregledno urno, ki vsebuje barvne kroglice in kroglice narišemo naključno. Ko narišemo kroglico, opazujemo njeno barvo, jo postavimo nazaj v urno in dodamo dodatno kroglico iste barve. Podobno shemo uporabljajo Blackwell in MacQueen za izdelavo Dirichletovega procesa.

Ta shema ustvari zaporedje θ₁, θ₂,… Z pogojne verjetnosti . V tej shemi predpostavljamo, da je G₀ je porazdelitev po barvah in vsaki θ_n predstavlja barvo kroglice, ki je nameščena v urni. The algoritem je, kot sledi:

· Začnemo s prazno urno.

· Z verjetnostjo sorazmerno z α rišemo in v urno dodamo kroglico te barve.

· Z verjetnostjo, sorazmerno n-1, narišemo naključno kroglico iz urne, opazujemo njeno barvo, jo postavimo nazaj k urni in v urno dodamo dodatno kroglico iste barve.

Prej smo začeli s postopkom Dirichlet in izpeljali shemo Blackwell-MacQueen. Zdaj začnimo obratno od sheme Blackwell-MacQueen in izpeljemo DP. Ker je θ_i so bili na Gid izrisani na enak način, njihova skupna porazdelitev bo invazivna na kakršne koli končne permutacije in so zato izmenljive. Posledično z uporabo teorema de Finetti moramo ugotoviti, da mora obstajati porazdelitev ukrepov, da bi postali ti, in ta distribucija je Dirichletov proces. Kot rezultat tega dokazujemo, da je urna shema Blackwell-MacQueen reprezentanca DP in nam daje konkreten način, da jo konstruiramo. Kot bomo videli kasneje, je ta shema matematično enakovredna kitajskemu restavracijskemu postopku.

3.2 Konstrukcija, ki lomi palice

Konstrukcija razbijanja palic je alternativni način predstavljanja Dirichletovega procesa, ki ga je uvedel podjetje Sethuraman. Gre za konstruktiven način oblikovanja distribucijo in uporablja po analogiji: Predvidevamo, da imamo palico dolžine 1, jo razbijemo na položaju β₁ in dodelimo π₁ enaka dolžini dela palice, ki smo ga zlomili. Isti postopek ponovimo, da dobimo π₂, π₃,… Itd; zaradi načina, kako je definirana ta shema, lahko nadaljujemo z neštetokrat.

Na podlagi zgoraj navedenega π_k lahko modeliramo kot , kje za medtem ko kot v prejšnjih shemah θ vzorčijo neposredno s porazdelitvijo baze . Posledično lahko porazdelitev G zapišemo kot vsoto delta funkcij, tehtanih z π_k verjetnosti, ki je enaka . Tako nam konstrukcija za razbijanje palic omogoča preprost in intuitiven način, kako sestaviti Dirichletov postopek.

3.3 Proces kitajske restavracije

Kitajski postopek restavracij, ki ga je uvedel Aldous, je še en učinkovit način predstavljanja Dirichletovega procesa in ga je mogoče neposredno povezati s shemo urne Blackwell-MacQueen. Ta shema uporablja po analogiji: Predvidevamo, da obstaja kitajska restavracija z neskončno veliko miz. Ko stranke vstopijo v restavracijo, naključno sedejo za katero koli zasedeno mizo ali pa se odločijo sedeti za prvo razpoložljivo prazno mizo.

CRP definira porazdelitev na prostor particij pozitivnih celih števil. Začnemo z risanjem θ₁,… Θ_n iz sheme urn Blackwell-MacQueen. Kot smo razpravljali v prejšnjih odsekih, pričakujemo, da bo viden učinek grozda in bo tako skupno število edinstvenih vrednosti θ k bistveno manjše od n. Tako to določa particijo niza {1,2, ..., n} v k skupinah. Posledično risanje iz sheme urnika Blackwell-MacQueen povzroči naključno particijo nabora {1,2,…, n}. Kitajska restavracija je to posledica razdelitev na predelne stene. Algoritem je naslednji:

· Začnemo s prazno restavracijo.

· 1^st stranka sedi vedno na 1^st miza

· N + 1^th stranka ima 2 možnosti:

o Z verjetnostjo sedite na 1. nezasedeno mizo

o Z verjetnostjo sedite na katero izmed kth zasedenih miz
Kje je število ljudi, ki sedijo za to mizo

Kjer je α disperzijska vrednost DP in n skupno število strank v restavraciji v določenem času. Latentna spremenljivka z_i shrani številko tabele i^th odjemalec in vzame vrednosti od 1 do k_n kjer k_n je skupno število zasedenih miz, ko je v restavraciji n kupcev. Opozoriti moramo, da je k_n bo vedno manj ali enak n in v povprečju znaša približno . Na koncu moramo opozoriti, da je verjetnost razporeditve tabel je invariantno do permutacij. Tako je z_i je izmenljivo, kar pomeni, da imajo mize z enako velikostjo kupcev enako verjetnost.

Kitajski restavracijski postopek je močno povezan s Pólya urno shemo in Dirichlet Process. CRP je način, kako določiti a razdelitev na predelne stene (razpredelnice tabele) n točk in jih je mogoče uporabiti kot prednost na prostoru latentne spremenljivke z_i ki določa dodelitve grozda. CRP je enakovredna Pólyevi shemi urn z le razliko, da ne dodeljuje parametrov vsaki tabeli / grozdu. Iti od CRP do Pólyine urne sheme rišemo za vse tabele k = 1,2… in nato za vsako x_i ki je združena v tabelo z_i dodelite a . Z drugimi besedami, dodelite novemu x_i parameter θ tabele. Končno od takrat ne moremo dodeliti θ do neskončnih tabel od začetka, lahko samo dodelimo novo θ vsakič, ko nekdo sedi za novo mizo. Zaradi vsega navedenega nam lahko CRP pomaga sestaviti računsko učinkovite algoritme za izvajanje analize grozdov na naboru podatkov.

V tej objavi smo razpravljali o postopku Dirichlet in več načinih, kako ga zgraditi. Zgornje ideje bomo uporabili v naslednjem članku. Uvedli bomo model mešanice procesa Dirichlet in uporabili bomo predstavništvo kitajskih restavracij za izdelavo Dirichletovega procesa in predoblikovanje grozdne analize. Če ste izpustili nekaj točk, ne skrbite, saj se bodo stvari z jasnimi začetki začele jasneje razviti z naslednjimi dvema člankoma.

Upam, da se vam zdi ta objava zanimiva. Če ste to storili, si vzemite trenutek, da ga delite na Facebooku in Twitterju. 🙂