1ICFO-Institut de Ciences Fotoniques, Barcelonski inštitut za znanost in tehnologijo, 08860 Castelldefels, Španija
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Španija
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Francija
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Španija
Se vam zdi ta članek zanimiv ali želite razpravljati? Zaslišite ali pustite komentar na SciRate.
Minimalizem
Medsebojno nepristranske baze ustrezajo zelo uporabnim parom meritev v kvantni informacijski teoriji. V najmanjši sestavljeni dimenziji, šest, je znano, da obstaja od tri do sedem medsebojno nepristranskih baz, pri čemer desetletja stara domneva, znana kot Zaunerjeva domneva, pravi, da obstajajo največ tri. Tukaj se lotimo Zaunerjeve domneve numerično s konstrukcijo Bellovih neenakosti za vsak par celih števil $n,d ge 2$, ki jih je mogoče maksimalno kršiti v dimenziji $d$, če in samo če v tej dimenziji obstaja $n$ MUB. Zato Zaunerjevo domnevo spremenimo v optimizacijski problem, ki ga obravnavamo s tremi numeričnimi metodami: optimizacijo nihanja, nelinearnim poldoločenim programiranjem in tehnikami Monte Carlo. Vse tri metode pravilno identificirajo znane primere v nizkih dimenzijah in vse nakazujejo, da v šesti dimenziji ne obstajajo štiri medsebojno nepristranske baze, pri čemer vse najdejo iste baze, ki numerično optimizirajo ustrezno Bellovo neenakost. Poleg tega se zdi, da ti numerični optimizatorji sovpadajo s »štirimi najbolj oddaljenimi bazami« v dimenziji šest, ki jih najdemo z numerično optimizacijo mere razdalje v [P. Raynal, X. Lü, B.-G. Englert, {Phys. Rev. A}, { 83} 062303 (2011)]. Končno rezultati Monte Carla kažejo, da v dimenziji deset obstajajo največ trije MUB.
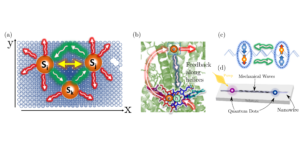
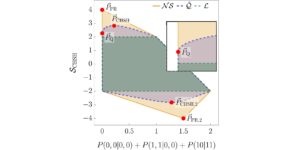
Predstavljena slika: Relativna razlika med vrednostjo naših Bellovih neenakosti ob predpostavki, da v dimenziji d obstaja n MUB, in vrednostjo, ugotovljeno z našimi numeričnimi metodami. Ničelne vrednosti pomenijo, da so metode našle n MUB-jev v dimenziji d, medtem ko neničelne vrednosti pomenijo, da metode niso našle n MUB-ov v dimenziji d. Vsi znani primeri (dimenzije od dve do pet in dimenzija šest z dvema in tremi MUB) so pravilno identificirani s številkami. V šesti dimenziji nobena od metod ne najde štirih MUB in vse metode konvergirajo k istemu nizu štirih baz.
Priljubljen povzetek
Kljub široki uporabi še vedno ostajajo odprta vprašanja glede strukture MUB. Najpomembneje je, da največje število meritev, ki so parno nepristranske (»število MUB«), ni znano, če je dimenzija kvantnega sistema sestavljeno število. Zlasti v šesti dimenziji vemo le, da je število MUB med tremi in sedmimi. Dolgoletna odprta domneva je Zaunerjeva, ki pravi, da v šesti dimenziji ne obstajajo več kot trije MUB. Ta desetletja trajajoča domneva je podprta z nekaterimi številčnimi dokazi, vendar do danes ni nobenega dokaza.
V tem delu se lotevamo Zaunerjeve domneve skozi Bellovo nelokalnost. Bellova nelokalnost zadeva dva eksperimentatorja, ki ne smeta komunicirati, vendar si lahko delita nekatere korelacije v obliki klasične naključnosti ali skupnega kvantnega stanja. Izkazalo se je, da lahko delitev kvantnih virov vodi do eksperimentalnih podatkov, ki jih klasična fizika (natančneje s t.i. lokalnimi skritimi modeli spremenljivk) ne more pojasniti. To je znano kot Bellov izrek in je bilo eksperimentalno preverjeno v zadnjem desetletju. Dokazovanje neklasičnosti eksperimentalnih podatkov se najpogosteje izvaja s tako imenovanimi Bellovimi neenakostmi, ki so funkcije verjetnosti izida meritev, ki se pojavljajo v eksperimentu. Klasični podatki morajo zadostiti Bellovim neenakostim, medtem ko jih kvantni podatki lahko kršijo.
Nedavno so bile ugotovljene Bellove neenakosti, ki so največje kršene, če ena od strani uporabi par meritev MUB dane dimenzije. V tem delu te neenakosti razširimo na nove, ki jih največkrat krši izbrano število meritev MUB v dani dimenziji. Poleg tega, če je dimenzija v poskusu fiksna, se doseže največja kršitev, če in samo če uporabljene meritve ustrezajo izbranemu številu MUB v dani dimenziji. Zato je odločitev, ali izbrano število MUB obstaja v dani dimenziji, enakovredna iskanju največje kršitve ustrezne Bellove neenakosti v tej fiksni dimenziji.
Čeprav je iskanje te največje kršitve na splošno težka težava, uporabljamo tri različne numerične metode, da bi našli največjo kršitev naših Bellovih neenakosti v fiksni dimenziji. Dve od teh metod sta različici tehnik poldoločenega programiranja, medtem ko se tretja zgleduje po statistični fiziki in se imenuje simulirano žarjenje. Medtem ko so vse te metode hevristične – to pomeni, da ni nobenega zagotovila, da bodo našle pravi optimum problema – lahko ocenimo njihovo učinkovitost tako, da jih uporabimo za optimizacijske probleme, katerih optimum je znan. Zlasti ugotavljamo, da lahko vse tri metode pravilno prepoznajo meritve MUB v primerih, ko je znano, da obstajajo. Poleg tega se v primerih, ko je znano, da ne obstajajo, vse tri metode konvergirajo k istemu naboru meritev do numerične natančnosti. Nato uporabimo naše metode za prvi neznani primer, to je štiri MUB v dimenziji šest. Nobena od metod ne more identificirati štirih MUB-jev v šesti dimenziji, vendar spet vse konvergirajo k istemu nizu štirih meritev do numerične natančnosti. Poleg tega tehnika simuliranega žarjenja ne najde štirih MUB v naslednji sestavljeni dimenziji, dimenziji deset. Zato, čeprav ni mogoče podati strogih trditev zaradi hevristične narave naših tehnik, naši rezultati podpirajo Zaunerjevo domnevo iz nove perspektive Bellove nelokalnosti.
► BibTeX podatki
► Reference
[1] ID Ivanović. Geometrijski opis določanja kvantnega stanja. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Kvantna kriptografija: distribucija javnih ključev in met kovancev. Zbornik mednarodnih konferenc IEEE o računalnikih, sistemih in obdelavi signalov (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] Artur K. Ekert. Kvantna kriptografija na podlagi Bellovega izreka. Phys. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] Dagmar Bruß. Optimalno prisluškovanje v kvantni kriptografiji s šestimi stanji. Phys. Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques in Mohamed Bourennane. Kvantne kode za naključni dostop z uporabo sistemov z enim nivojem $d$. Phys. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas in Jędrzej Kaniewski. Samotestiranje vzajemno nepristranskih baz v scenariju pripravi in meri. Phys. Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci in N. Gisin. Bellova neenakost za k-enote z binarnimi meritvami. Kvantne informacije. Računalništvo, 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos in Remigiusz Augusiak. Največja nelokalnost iz maksimalne zapletenosti in medsebojno nepristranskih baz ter samotestiranje kvantnih sistemov z dvema qutritoma. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal in Jędrzej Kaniewski. Vzajemno nepristranske baze in simetrične informacijsko popolne meritve v Bellovih poskusih. Znanstveni napredek, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson in Karol Życzkowski. Na vzajemno nepristranskih osnovah. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] William K Wootters in Brian D Fields. Določitev optimalnega stanja z medsebojno nepristranskimi meritvami. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan in Thomas Beth. Novogradnja medsebojno nepristranskih baz v kvadratnih dimenzijah. Kvantne informacije. Računalništvo, 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[13] Mihály Weiner. Vrzel za največje število medsebojno nepristranskih baz. Proc. Amer. matematika Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Doktorska disertacija, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep in Pawel Wocjan. Medsebojno nepristranske baze in ortogonalne dekompozicije Liejevih algeber. Kvantne informacije. Računalništvo, 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[16] Stephen Brierley in Stefan Weigert. Konstruiranje medsebojno nepristranskih baz v šesti dimenziji. Phys. Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi in Mihály Weiner. Posplošen Paulijev problem in neskončna družina MUB-trojčkov v dimenziji 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, maj 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer in Afaq Tahir. Dokazi za in proti Zaunerjevi domnevi MUB v $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling in Sven Polak. Medsebojno nepristranske baze: polinomska optimizacija in simetrija. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej in Karol Życzkowski. Medsebojno nepristranske baze in Hadamardove matrike šestega reda. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] Philippe Raynal, Xin Lü in Berthold-Georg Englert. Medsebojno nepristranske baze v šestih dimenzijah: štiri najbolj oddaljene baze. Phys. Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz in Marcin Pawłowski. Povezave med medsebojno nepristranskimi bazami in kvantnimi kodami za naključni dostop. Phys. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani in Stephanie Wehner. Nelokalnost zvonca. Rev. Mod. Phys., 86: 419–478, 2014. doi: 10.1103 / RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOSEK ApS. MOSEK Fusion API za C++ 9.2.49, 2021. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe in Kouhei Harada. Metoda primarnih in dvojnih notranjih točk za nelinearno poldefinitno programiranje. Matematično programiranje, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] Stephen Boyd in Lieven Vandenberghe. Konveksna optimizacija. Cambridge University Press, 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt in MP Vecchi. Optimizacija s simuliranim žarjenjem. Znanost, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / znanost.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller in Edward Teller. Enačba izračunov stanja hitrih računskih strojev. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] Miguel Navascués, Stefano Pironio in Antonio Acín. Omejitev niza kvantnih korelacije. Phys. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Navedel
Ta dokument je objavljen v Quantumu pod Priznanje avtorstva Creative Commons 4.0 International (CC BY 4.0) licenca. Avtorske pravice ostajajo pri izvirnih imetnikih avtorskih pravic, kot so avtorji ali njihove ustanove.