'การพึมพำ' ของเส้นโค้งรูปไข่พบกับ AI Take Flight | นิตยสารควอนต้า

เส้นโค้งรูปวงรีเป็นหนึ่งในวัตถุที่ล่อลวงในคณิตศาสตร์สมัยใหม่ ดูเหมือนไม่ซับซ้อน แต่สร้างทางด่วนระหว่างคณิตศาสตร์ที่หลายคนเรียนในโรงเรียนมัธยมปลายกับการวิจัยคณิตศาสตร์อย่างลึกซึ้งที่สุด พวกเขาเป็นศูนย์กลางของการพิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาต์ที่โด่งดังของ Andrew Wiles ในทศวรรษ 1990 เป็นเครื่องมือสำคัญในการเข้ารหัสสมัยใหม่ และในปี พ.ศ. 2000 สถาบันคณิตศาสตร์เคลย์ได้ตั้งชื่อว่า ก การคาดเดาเกี่ยวกับสถิติ ของเส้นโค้งรูปไข่หนึ่งในเจ็ด "ปัญหารางวัลมิลเลนเนียม" ซึ่งแต่ละข้อจะได้รับรางวัล 1 ล้านดอลลาร์สำหรับการแก้ปัญหา การคาดเดานั้นเริ่มแรกโดย ไบรอัน เบิร์ช และ ปีเตอร์ สวินเนอร์ตัน-ไดเออร์ ในทศวรรษ 1960 ยังไม่ได้รับการพิสูจน์

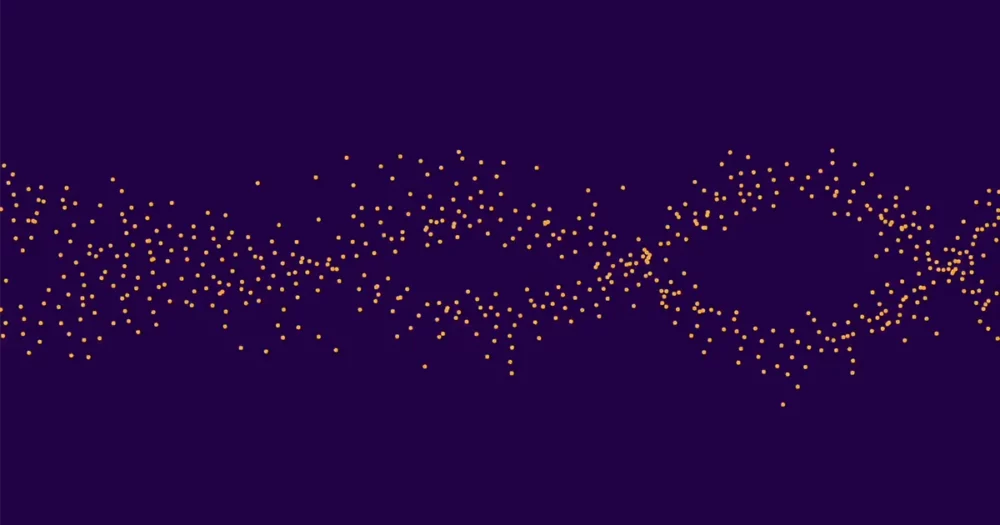
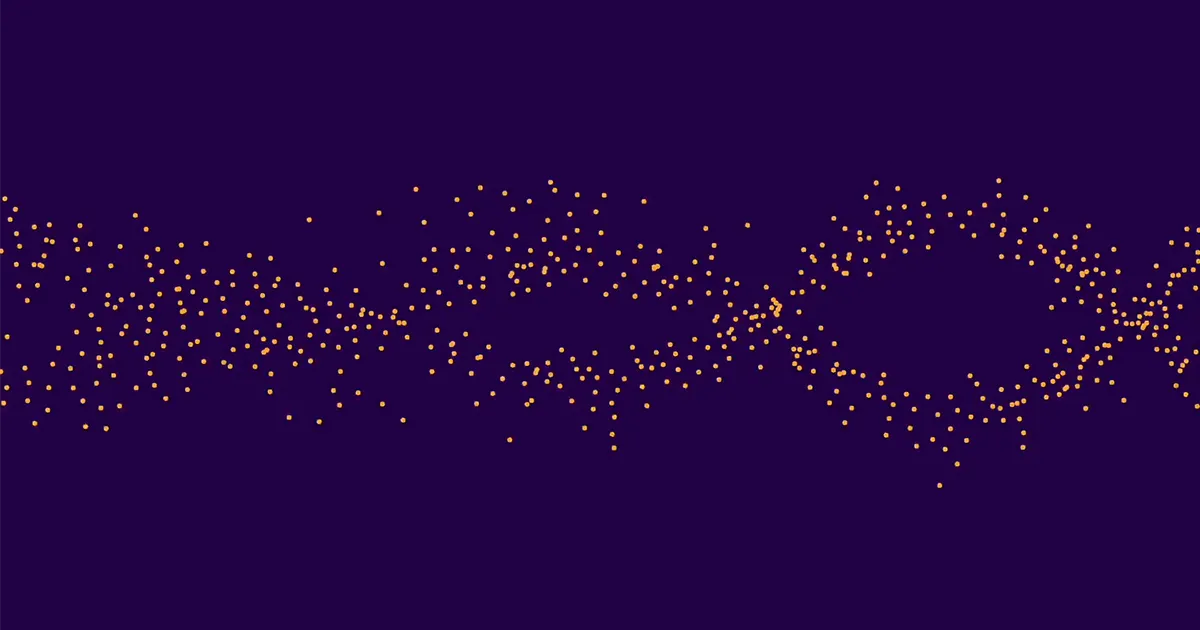
การทำความเข้าใจเส้นโค้งวงรีเป็นความพยายามที่มีเดิมพันสูงซึ่งเป็นศูนย์กลางของคณิตศาสตร์ ดังนั้นในปี 2022 เมื่อความร่วมมือข้ามมหาสมุทรแอตแลนติกใช้เทคนิคทางสถิติและปัญญาประดิษฐ์ในการค้นพบรูปแบบที่ไม่คาดคิดโดยสิ้นเชิงในเส้นโค้งรูปไข่ ถือเป็นการมีส่วนร่วมที่น่ายินดีหากไม่คาดคิด “มันเป็นเรื่องของเวลาก่อนที่แมชชีนเลิร์นนิงจะมาถึงหน้าประตูบ้านเราพร้อมกับสิ่งที่น่าสนใจ” กล่าว ปีเตอร์ สารนักเป็นนักคณิตศาสตร์ที่สถาบันการศึกษาขั้นสูงและมหาวิทยาลัยพรินซ์ตัน ในตอนแรกไม่มีใครสามารถอธิบายได้ว่าทำไมรูปแบบที่เพิ่งค้นพบจึงมีอยู่ นับตั้งแต่นั้นเป็นต้นมา ในรายงานชุดล่าสุด นักคณิตศาสตร์ได้เริ่มไขเหตุผลเบื้องหลังรูปแบบนี้ ซึ่งเรียกว่า "การพึมพำ" เนื่องจากมีความคล้ายคลึงกับรูปร่างของเหลวของนกกิ้งโครงฝูง และเริ่มพิสูจน์ว่าสิ่งเหล่านี้จะต้องเกิดขึ้นไม่เพียงแต่ในโดยเฉพาะเท่านั้น ตัวอย่างที่ได้รับการตรวจสอบในปี 2022 แต่โดยทั่วไปจะเป็นเส้นโค้งรูปไข่มากกว่า

ความสำคัญของการเป็นรูปไข่

เพื่อทำความเข้าใจว่ารูปแบบเหล่านั้นคืออะไร เราต้องวางรากฐานเล็กน้อยว่าเส้นโค้งวงรีคืออะไร และนักคณิตศาสตร์จัดหมวดหมู่พวกมันอย่างไร

เส้นโค้งรูปวงรีเกี่ยวข้องกับกำลังสองของตัวแปรตัวหนึ่ง โดยทั่วไปเขียนเป็น yยกกำลังสามของอีกอัน โดยทั่วไปเขียนว่า x: y² = x³ + Ax + Bสำหรับตัวเลขบางคู่ A และ Bตราบใดที่ A และ B ตรงตามเงื่อนไขบางประการ สมการนี้กำหนดเส้นโค้งที่สามารถวาดกราฟได้บนระนาบ ดังที่แสดงด้านล่าง (แม้ว่าชื่อจะคล้ายกัน แต่วงรีก็ไม่ใช่เส้นโค้งวงรี)

แม้ว่าเส้นโค้งรูปไข่จะดูธรรมดา แต่กลับกลายเป็นเครื่องมือที่ทรงพลังอย่างเหลือเชื่อสำหรับนักทฤษฎีจำนวน นักคณิตศาสตร์ที่มองหารูปแบบในจำนวนเต็ม แทนที่จะปล่อยให้ตัวแปร x และ y ช่วงของตัวเลขทั้งหมด นักคณิตศาสตร์ชอบจำกัดให้ระบบตัวเลขต่างกัน ซึ่งพวกเขาเรียกว่าการกำหนดเส้นโค้ง "เหนือ" ระบบตัวเลขที่กำหนด เส้นโค้งวงรีจำกัดเฉพาะจำนวนตรรกยะ — ตัวเลขที่สามารถเขียนเป็นเศษส่วนได้ — มีประโยชน์อย่างยิ่ง “เส้นโค้งวงรีเหนือจำนวนจริงหรือจำนวนเชิงซ้อนนั้นค่อนข้างน่าเบื่อ” ซาร์นัคกล่าว “มีเพียงจำนวนตรรกยะเท่านั้นที่ลึกซึ้ง”

นี่เป็นวิธีหนึ่งที่เป็นจริง หากคุณวาดเส้นตรงระหว่างจุดจำนวนตรรกยะสองจุดบนเส้นโค้งวงรี จุดที่เส้นนั้นตัดกับเส้นโค้งอีกครั้งก็จะถือเป็นตรรกยะเช่นกัน คุณสามารถใช้ข้อเท็จจริงนั้นเพื่อกำหนด "การบวก" ในเส้นโค้งรูปวงรี ดังที่แสดงด้านล่าง

ลากเส้นระหว่าง P และ Q. เส้นนั้นจะตัดเส้นโค้งที่จุดที่สาม R. (นักคณิตศาสตร์มีเคล็ดลับพิเศษในการจัดการกับกรณีที่เส้นไม่ตัดเส้นโค้งโดยบวก "จุดที่อนันต์") การสะท้อนของ R ข้าม x-axis คือผลรวมของคุณ P + Q. เมื่อรวมกับการดำเนินการบวกนี้ คำตอบทั้งหมดของเส้นโค้งจะก่อให้เกิดวัตถุทางคณิตศาสตร์ที่เรียกว่ากลุ่ม

นักคณิตศาสตร์ใช้สิ่งนี้เพื่อกำหนด "อันดับ" ของเส้นโค้ง ที่ อันดับของเส้นโค้ง เกี่ยวข้องกับจำนวนวิธีแก้ปัญหาเชิงตรรกศาสตร์ที่มี เส้นโค้งอันดับ 0 มีจำนวนคำตอบจำกัด เส้นโค้งที่มีอันดับสูงกว่าจะมีคำตอบจำนวนอนันต์ ซึ่งความสัมพันธ์ระหว่างกันโดยใช้การดำเนินการบวกจะอธิบายตามอันดับ

อันดับยังไม่เป็นที่เข้าใจดีนัก นักคณิตศาสตร์ไม่มีวิธีคำนวณเสมอไป และไม่รู้ว่าจะคำนวณได้มากขนาดไหน (อันดับที่แน่นอนที่สุดที่ทราบสำหรับเส้นโค้งหนึ่งๆ คือ 20) เส้นโค้งที่ดูคล้ายกันสามารถมีอันดับที่แตกต่างกันโดยสิ้นเชิง

เส้นโค้งวงรียังเกี่ยวข้องกับจำนวนเฉพาะอย่างมาก ซึ่งหารด้วย 1 และตัวมันเองเท่านั้น โดยเฉพาะอย่างยิ่ง นักคณิตศาสตร์จะพิจารณาเส้นโค้งเหนือเขตข้อมูลจำกัด ซึ่งเป็นระบบเลขคณิตแบบวัฏจักรที่กำหนดไว้สำหรับจำนวนเฉพาะแต่ละตัว สนามที่มีขอบเขตจำกัดเปรียบเสมือนนาฬิกาที่มีจำนวนชั่วโมงเท่ากับจำนวนเฉพาะ หากคุณนับไปเรื่อยๆ ตัวเลขจะเริ่มต้นใหม่อีกครั้ง ตัวอย่างเช่น ในฟิลด์จำกัดของ 7 5 บวก 2 เท่ากับศูนย์ และ 5 บวก 3 เท่ากับ 1

เส้นโค้งรูปวงรีมีลำดับตัวเลขที่เกี่ยวข้องกัน เรียกว่า a_pซึ่งเกี่ยวข้องกับจำนวนคำตอบที่มีกับเส้นโค้งในสนามจำกัดที่กำหนดโดยจำนวนเฉพาะ p. มีขนาดเล็กกว่า a_p หมายถึงการแก้ปัญหาเพิ่มเติม ใหญ่กว่า a_p หมายถึงการแก้ปัญหาน้อยลง แม้ว่าอันดับจะคำนวณได้ยาก แต่ลำดับ a_p ง่ายกว่ามาก

บนพื้นฐานของการคำนวณจำนวนมากที่ทำบนคอมพิวเตอร์เครื่องแรกๆ เครื่องหนึ่ง Birch และ Swinnerton-Dyer คาดเดาความสัมพันธ์ระหว่างอันดับของเส้นโค้งวงรีและลำดับ a_p. ใครก็ตามที่สามารถพิสูจน์ได้ว่าพวกเขาพูดถูกจะได้รับรางวัลล้านดอลลาร์และความเป็นอมตะทางคณิตศาสตร์

รูปแบบที่น่าประหลาดใจปรากฏขึ้น

หลังจากเริ่มมีการระบาดใหญ่ หยางฮุยเหอนักวิจัยจาก London Institute for Mathematical Sciences ได้ตัดสินใจที่จะเผชิญกับความท้าทายใหม่ๆ เขาเคยเรียนวิชาเอกฟิสิกส์ในวิทยาลัย และได้รับปริญญาเอกจากสถาบันเทคโนโลยีแมสซาชูเซตส์ สาขาฟิสิกส์คณิตศาสตร์ แต่เขาสนใจทฤษฎีจำนวนมากขึ้น และด้วยความสามารถที่เพิ่มขึ้นของปัญญาประดิษฐ์ เขาคิดว่าเขาจะลองใช้ AI เป็นเครื่องมือในการค้นหารูปแบบตัวเลขที่ไม่คาดคิด (เขาเคยเป็นอยู่แล้ว โดยใช้แมชชีนเลิร์นนิง เพื่อจำแนก ท่อร่วม Calabi-Yauโครงสร้างทางคณิตศาสตร์ที่ใช้กันอย่างแพร่หลายในทฤษฎีสตริง)

ในเดือนสิงหาคม 2020 ขณะที่การแพร่ระบาดรุนแรงขึ้น มหาวิทยาลัยนอตติงแฮม ได้เป็นเจ้าภาพจัดงาน พูดคุยออนไลน์. เขามองโลกในแง่ร้ายเกี่ยวกับความก้าวหน้าของเขา และเกี่ยวกับความเป็นไปได้ที่จะใช้แมชชีนเลิร์นนิงเพื่อค้นพบคณิตศาสตร์ใหม่ๆ “การเล่าเรื่องของเขาคือทฤษฎีจำนวนนั้นยากเพราะคุณไม่สามารถเรียนรู้เกี่ยวกับเครื่องจักรในทฤษฎีจำนวนได้” กล่าว โทมัสโอลิเวอร์ซึ่งเป็นนักคณิตศาสตร์จากมหาวิทยาลัยเวสต์มินสเตอร์ซึ่งอยู่ในกลุ่มผู้ฟัง ดังที่พระองค์ทรงจำได้ “ฉันไม่พบสิ่งใดเลยเพราะฉันไม่ใช่ผู้เชี่ยวชาญ ฉันไม่ได้ใช้สิ่งที่ถูกต้องในการดูสิ่งนี้ด้วยซ้ำ”

โอลิเวอร์และ คยูฮวาน ลีนักคณิตศาสตร์จากมหาวิทยาลัยคอนเนตทิคัตเริ่มทำงานร่วมกับเขา “เราตัดสินใจทำเช่นนี้เพียงเพื่อเรียนรู้ว่าแมชชีนเลิร์นนิงคืออะไร แทนที่จะศึกษาคณิตศาสตร์อย่างจริงจัง” Oliver กล่าว “แต่เราพบอย่างรวดเร็วว่าคุณสามารถเรียนรู้เกี่ยวกับเครื่องจักรได้หลายอย่าง”

โอลิเวอร์และลีแนะนำให้เขาใช้เทคนิคของเขาในการตรวจสอบ L-ฟังก์ชั่น อนุกรมอนันต์ที่เกี่ยวข้องอย่างใกล้ชิดกับเส้นโค้งรูปไข่ผ่านลำดับ a_p. พวกเขาสามารถใช้ฐานข้อมูลออนไลน์ของเส้นโค้งรูปไข่และที่เกี่ยวข้อง L- ฟังก์ชั่นที่เรียกว่า แอลเอ็มเอฟดีบี เพื่อฝึกตัวแยกประเภทแมชชีนเลิร์นนิง ในขณะนั้นฐานข้อมูลมีเส้นโค้งรูปไข่มากกว่า 3 ล้านเส้นเล็กน้อยเหนือเหตุผล ภายในเดือนตุลาคม 2020 พวกเขามี กระดาษ ที่ใช้ข้อมูลที่รวบรวมมาจาก L-ฟังก์ชั่นในการทำนายคุณสมบัติเฉพาะของเส้นโค้งรูปไข่ ในเดือนพฤศจิกายนพวกเขาแบ่งปัน กระดาษอีกแผ่น ที่ใช้การเรียนรู้ของเครื่องเพื่อจำแนกวัตถุอื่นๆ ในทฤษฎีจำนวน ภายในเดือนธันวาคมพวกเขาสามารถ ทำนายอันดับของเส้นโค้งรูปไข่ มีความแม่นยำสูง

แต่พวกเขาไม่แน่ใจว่าเหตุใดอัลกอริธึมการเรียนรู้ของเครื่องจึงทำงานได้ดีนัก Lee ถาม Alexey Pozdnyakov นักศึกษาระดับปริญญาตรีของเขาเพื่อดูว่าเขาสามารถเข้าใจสิ่งที่เกิดขึ้นได้หรือไม่ เมื่อมันเกิดขึ้น LMFDB จะเรียงลำดับเส้นโค้งรูปไข่ตามปริมาณที่เรียกว่าตัวนำ ซึ่งจะสรุปข้อมูลเกี่ยวกับจำนวนเฉพาะที่เส้นโค้งทำงานได้ไม่ดี ดังนั้น Pozdnyakov จึงพยายามดูเส้นโค้งจำนวนมากที่มีตัวนำที่คล้ายกันพร้อมกัน เช่น เส้นโค้งทั้งหมดที่มีตัวนำระหว่าง 7,500 ถึง 10,000

มีจำนวนโค้งทั้งหมดประมาณ 10,000 โค้ง ประมาณครึ่งหนึ่งมีอันดับ 0 และอีกครึ่งหนึ่งมีอันดับ 1 (อันดับสูงกว่านั้นหายากมาก) จากนั้นเขาก็เฉลี่ยค่าของ a_p สำหรับเส้นโค้งอันดับ 0 ทั้งหมด เฉลี่ยแยกกัน a_p สำหรับเส้นโค้งอันดับ 1 ทั้งหมด และวางแผนผลลัพธ์ จุดทั้งสองชุดก่อตัวเป็นคลื่นสองอันที่แตกต่างกันและมองเห็นได้ง่าย นั่นคือเหตุผลที่ตัวแยกประเภทแมชชีนเลิร์นนิงสามารถยืนยันอันดับของเส้นโค้งเฉพาะได้อย่างถูกต้อง

“ตอนแรกฉันรู้สึกมีความสุขที่ได้ทำงานมอบหมายนี้เสร็จ” พอซดเนียคอฟกล่าว “แต่คยูฮวานรู้ทันทีว่ารูปแบบนี้น่าประหลาดใจ และนั่นคือตอนที่มันน่าตื่นเต้นจริงๆ”

ลีและโอลิเวอร์ติดใจ “Alexey เอารูปนี้มาให้เราดู และฉันก็บอกว่ามันดูเหมือนนกทำแบบนั้น” Oliver กล่าว “แล้วคยูฮวานก็เงยหน้าขึ้นและบอกว่ามันเรียกว่าการบ่น แล้วหยางก็บอกว่าเราควรเรียกกระดาษนี้ว่า 'การพึมพำของ Elliptic Curves. '”

พวกเขาอัปโหลดรายงานในเดือนเมษายน 2022 และส่งต่อให้กับนักคณิตศาสตร์คนอื่นๆ จำนวนหนึ่ง โดยคาดหวังอย่างกังวลว่าจะได้รับแจ้งว่าสิ่งที่เรียกว่า "การค้นพบ" ของพวกเขาเป็นที่รู้จักกันดี โอลิเวอร์กล่าวว่าความสัมพันธ์นั้นมองเห็นได้ชัดเจนจนควรสังเกตมานานแล้ว

เกือบจะในทันที งานพิมพ์ล่วงหน้าก็ได้รับความสนใจ โดยเฉพาะจาก แอนดรูว์ซัทเธอร์แลนด์นักวิทยาศาสตร์การวิจัยของ MIT ซึ่งเป็นหนึ่งในบรรณาธิการบริหารของ LMFDB ซูเธอร์แลนด์ตระหนักว่าเส้นโค้งรูปวงรี 3 ล้านเส้นนั้นไม่เพียงพอสำหรับจุดประสงค์ของเขา เขาต้องการดูช่วงของตัวนำที่ใหญ่กว่ามากเพื่อดูว่าเสียงพึมพำนั้นแข็งแกร่งแค่ไหน เขาดึงข้อมูลจากแหล่งเก็บข้อมูลขนาดใหญ่อีกแห่งซึ่งมีเส้นโค้งรูปไข่ประมาณ 150 ล้านเส้น ยังคงไม่พอใจ จากนั้นเขาก็ดึงข้อมูลจากพื้นที่เก็บข้อมูลอื่นที่มีเส้นโค้ง 300 ล้านเส้น

“แต่ถึงอย่างนั้นก็ยังไม่เพียงพอ ดังนั้นฉันจึงคำนวณชุดข้อมูลใหม่ของเส้นโค้งวงรีมากกว่าหนึ่งพันล้านเส้น และนั่นคือสิ่งที่ฉันใช้ในการคำนวณภาพที่มีความละเอียดสูงจริงๆ” ซัทเทอร์แลนด์กล่าว เสียงพึมพำปรากฏขึ้นว่าเขามีเส้นโค้งรูปไข่เฉลี่ยมากกว่า 15,000 เส้นโค้งในแต่ละครั้งหรือครั้งละล้านครั้ง รูปร่างยังคงเหมือนเดิมแม้ในขณะที่เขามองดูเส้นโค้งเหนือจำนวนเฉพาะที่มากขึ้นเรื่อยๆ ซึ่งเป็นปรากฏการณ์ที่เรียกว่าความแปรปรวนของสเกล ซูเธอร์แลนด์ยังตระหนักด้วยว่าการพึมพำไม่ได้มีลักษณะเฉพาะกับเส้นโค้งรูปไข่ แต่ยังปรากฏโดยทั่วไปมากกว่าด้วย L-ฟังก์ชั่น. เขาเขียน จดหมายสรุปการค้นพบของเขา และส่งไปให้สารนาคและ ไมเคิล รูบินสไตน์ ที่มหาวิทยาลัยวอเตอร์ลู

“หากมีคำอธิบายที่รู้อยู่แล้ว ฉันคาดหวังว่าคุณจะรู้” ซัทเทอร์แลนด์เขียน

พวกเขาไม่ได้

อธิบายรูปแบบ

Lee, He และ Oliver จัดเวิร์กช็อปเกี่ยวกับการบ่นในเดือนสิงหาคม 2023 ที่สถาบันวิจัยคณิตศาสตร์และการทดลองทางคณิตศาสตร์ของมหาวิทยาลัยบราวน์ (ICERM) Sarnak และ Rubinstein ก็มา เช่นเดียวกับลูกศิษย์ของ Sarnak นีน่า ซูบริลินา.

Zubrilina นำเสนองานวิจัยของเธอเกี่ยวกับรูปแบบการบ่นใน แบบฟอร์มโมดูลาร์ฟังก์ชันพิเศษที่ซับซ้อนซึ่งเชื่อมโยงกัน เช่นเดียวกับเส้นโค้งวงรี L-ฟังก์ชั่น. ในรูปแบบโมดูลาร์ที่มีตัวนำขนาดใหญ่ เสียงพึมพำมาบรรจบกันเป็นเส้นโค้งที่กำหนดไว้อย่างชัดเจน แทนที่จะสร้างรูปแบบที่มองเห็นได้แต่กระจัดกระจาย ใน กระดาษ โพสต์เมื่อวันที่ 11 ตุลาคม 2023 Zubrilina พิสูจน์ว่าการบ่นประเภทนี้เป็นไปตามสูตรที่ชัดเจนที่เธอค้นพบ

“ความสำเร็จที่ยิ่งใหญ่ของนีน่าคือการที่เธอได้กำหนดสูตรสำหรับสิ่งนี้ ฉันเรียกมันว่าสูตรความหนาแน่นของการพึมพำของ Zubrilina” Sarnak กล่าว “ด้วยการใช้คณิตศาสตร์ที่ซับซ้อนมาก เธอได้พิสูจน์สูตรที่แน่นอนซึ่งเหมาะกับข้อมูลอย่างสมบูรณ์แบบ”

สูตรของเธอมีความซับซ้อน แต่ Sarnak ยกย่องให้เป็นฟังก์ชันรูปแบบใหม่ที่สำคัญ เทียบได้กับฟังก์ชัน Airy ที่กำหนดคำตอบของสมการเชิงอนุพันธ์ที่ใช้ในบริบทต่างๆ ในฟิสิกส์ ตั้งแต่ทัศนศาสตร์ไปจนถึงกลศาสตร์ควอนตัม

แม้ว่าสูตรของ Zubrilina จะเป็นสูตรแรก แต่ก็มีสูตรอื่นๆ ตามมา “ตอนนี้ทุกสัปดาห์ จะมีรายงานฉบับใหม่ออกมา” Sarnak กล่าว “ใช้เครื่องมือของ Zubrilina เป็นหลัก เพื่ออธิบายแง่มุมอื่นๆ ของการบ่น”

โจนาธาน โบเบอร์, แอนดรูว์ บูเกอร์ และ มินลี ของมหาวิทยาลัยบริสตอล ร่วมกับ เดวิด โลว์รี-ดูดา ของ ICERM ได้พิสูจน์การมีอยู่ของการบ่นประเภทต่างๆ ในรูปแบบโมดูลาร์ใน กระดาษเดือนตุลาคมอีกฉบับ. และ Kyu-Hwan Lee, Oliver และ Pozdnyakov พิสูจน์ความมีอยู่จริง ของการพึมพำในวัตถุที่เรียกว่าอักขระดิริชเลต์ที่มีความเกี่ยวข้องอย่างใกล้ชิด L-ฟังก์ชั่น.

ซูเธอร์แลนด์รู้สึกประทับใจกับโชคลาภมากมายที่นำไปสู่การค้นพบเสียงพึมพำ หากตัวนำไม่ได้เรียงลำดับข้อมูลเส้นโค้งรูปไข่ เสียงพึมพำก็จะหายไป “พวกเขาโชคดีที่ได้รับข้อมูลจาก LMFDB ซึ่งได้รับการจัดเรียงล่วงหน้าตามผู้ควบคุมวง” เขากล่าว “มันคือสิ่งที่เกี่ยวข้องกับเส้นโค้งรูปวงรีกับรูปแบบโมดูลาร์ที่สอดคล้องกัน แต่นั่นไม่ได้ชัดเจนเลย … เส้นโค้งสองเส้นที่สมการดูคล้ายกันมากสามารถมีตัวนำต่างกันมากได้” ตัวอย่างเช่น ซูเธอร์แลนด์ตั้งข้อสังเกตว่า y² = x³ - 11x + 6 มีตัวนำ 17 แต่กลับเครื่องหมายลบเป็นเครื่องหมายบวก y² = x³ + 11x +6 มีตัวนำ 100,736

ถึงกระนั้นก็ยังพบเสียงพึมพำเพียงเพราะขาดประสบการณ์ของ Pozdnyakov “ฉันไม่คิดว่าเราจะพบมันได้หากไม่มีเขา” โอลิเวอร์กล่าว “เพราะว่าผู้เชี่ยวชาญมักจะทำให้เป็นมาตรฐาน a_p ให้มีค่าสัมบูรณ์ 1 แต่เขาไม่ได้ทำให้พวกมันเป็นมาตรฐาน … ดังนั้นการแกว่งจึงใหญ่มากและมองเห็นได้”

รูปแบบทางสถิติที่อัลกอริธึม AI ใช้เพื่อจัดเรียงเส้นโค้งรูปไข่ตามอันดับมีอยู่ในพื้นที่พารามิเตอร์ที่มีหลายร้อยมิติ ซึ่งมากเกินไปสำหรับคนที่จะจัดเรียงในใจ ไม่ต้องพูดถึงการมองเห็น Oliver กล่าว แม้ว่าแมชชีนเลิร์นนิงจะพบความผันผวนที่ซ่อนอยู่ “แต่ต่อมาเราจึงเข้าใจว่ามันเป็นเสียงพึมพำ”

หมายเหตุบรรณาธิการ: Andrew Sutherland, Kyu-Hwan Lee และ L-functions และฐานข้อมูลรูปแบบโมดูลาร์ (LMFDB) ได้รับเงินทุนทั้งหมดจากมูลนิธิ Simons ซึ่งให้ทุนสนับสนุนสิ่งพิมพ์อิสระด้านบรรณาธิการนี้ด้วย การตัดสินใจให้ทุนสนับสนุนของมูลนิธิ Simons ไม่มีอิทธิพลต่อความคุ้มครองของเรา ข้อมูลเพิ่มเติมมีอยู่ โปรดคลิกที่นี่เพื่ออ่านรายละเอียดเพิ่มเติม.