นักคณิตศาสตร์ทอยลูกเต๋าและรับเป่ายิ้งฉุบ

ขณะที่ Bill Gates เล่าเรื่อง Warren Buffett เคยท้าทายเขาให้เล่นเกมลูกเต๋า แต่ละคนจะเลือกลูกเต๋าหนึ่งในสี่ลูกที่เป็นของบัฟเฟตต์ จากนั้นพวกเขาก็ทอย โดยหมายเลขที่สูงกว่าจะชนะ นี่ไม่ใช่ลูกเต๋ามาตรฐาน — พวกมันมีชุดตัวเลขที่แตกต่างจากปกติ 1 ถึง 6 บัฟเฟตต์เสนอให้ Gates เลือกก่อน เพื่อที่เขาจะได้เลือกลูกเต๋าที่แข็งแกร่งที่สุด แต่หลังจากที่ Gates ตรวจดูลูกเต๋า เขากลับเสนอข้อโต้แย้ง: บัฟเฟตต์ควรเลือกก่อน

เกตส์ตระหนักดีว่าลูกเต๋าของบัฟเฟตต์แสดงคุณสมบัติที่น่าสงสัย: ไม่มีใครที่แข็งแกร่งที่สุด ถ้าเกทส์เลือกก่อน แล้วไม่ว่าเขาจะเลือกลูกเต๋าไหน บัฟเฟตต์ก็จะสามารถหาลูกเต๋าอื่นที่สามารถเอาชนะได้ (นั่นคือ ลูกเต๋าที่มีโอกาสชนะมากกว่า 50%)

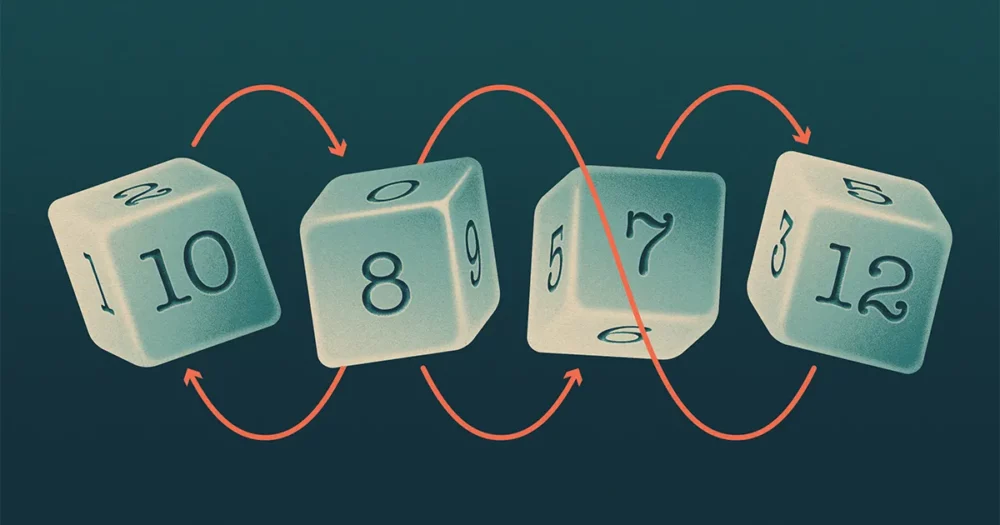
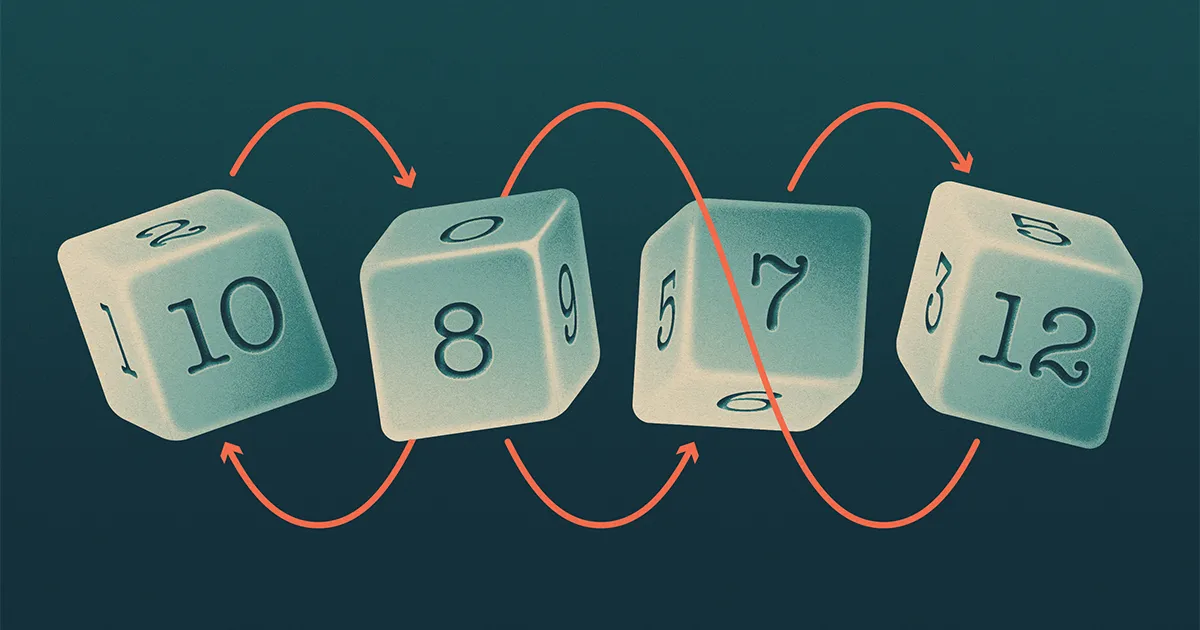
ลูกเต๋าสี่ลูกของบัฟเฟตต์ (เรียกว่า A, B, C และ D) เกิดเป็นรูปแบบที่ชวนให้นึกถึงการเป่ายิ้งฉุบซึ่ง A เต้น B, B เต้น C, C เต้น D และ D เต้น A. นักคณิตศาสตร์กล่าวว่าชุดลูกเต๋าดังกล่าวเป็น "อกรรมกริยา"

“มันไม่ง่ายเลยที่ [อกรรมกริยาลูกเต๋า] ควรจะมีด้วยซ้ำ” กล่าว ไบรอัน คอนรีย์ผู้อำนวยการของ American Institute of Mathematics (AIM) ในเมืองซานโฮเซ ผู้เขียนบทความเกี่ยวกับเรื่องนี้ในปี 2013

นักคณิตศาสตร์มาพร้อมกับ ตัวอย่างแรก ของลูกเต๋าอกรรมกริยาเมื่อกว่า 50 ปีก่อน และในที่สุด พิสูจน์แล้วว่า เมื่อคุณพิจารณาลูกเต๋าที่มีด้านมากขึ้นเรื่อยๆ คุณสามารถสร้างวัฏจักรอกรรมกริยาที่มีความยาวเท่าไรก็ได้ สิ่งที่นักคณิตศาสตร์ไม่รู้มาก่อนก็คือลูกเต๋าอกรรมกริยาทั่วไปเป็นอย่างไร คุณต้องประดิษฐ์ตัวอย่างอย่างระมัดระวังหรือคุณสามารถสุ่มเลือกลูกเต๋าและมีโอกาสที่ดีในการหาชุดอกรรมกริยา?

ดูลูกเต๋าสามลูกถ้าคุณรู้ A เต้น B และ B เต้น Cซึ่งดูเหมือนจะเป็นหลักฐานว่า A แข็งแกร่งที่สุด สถานการณ์ที่ C เต้น A น่าจะหายาก และแน่นอนว่าหากตัวเลขบนลูกเต๋ารวมกันเป็นผลรวมต่างๆ ได้ นักคณิตศาสตร์ก็เชื่อว่าสัญชาตญาณนี้ถือเป็นจริง

แต่ a กระดาษโพสต์ออนไลน์ ปลายปีที่แล้วแสดงให้เห็นว่าในสถานการณ์ธรรมชาติอื่น สัญชาตญาณนี้ล้มเหลวอย่างน่าทึ่ง สมมติว่าคุณต้องการให้ลูกเต๋าใช้เฉพาะตัวเลขที่ปรากฏในการทอยปกติและมีผลรวมเท่ากับการทอยปกติ จากนั้นกระดาษแสดงให้เห็นว่าถ้า A เต้น B และ B เต้น C, A และ C มีโอกาสที่จะชนะซึ่งกันและกันโดยพื้นฐานแล้ว

"รู้ว่า A เต้น B และ B เต้น C เพียงแค่ไม่ให้ข้อมูลเกี่ยวกับว่า A เต้น C," กล่าว ทิโมธี โกเวอร์ส จากมหาวิทยาลัยเคมบริดจ์ ผู้ชนะเลิศรางวัล Fields และหนึ่งในผู้มีส่วนร่วมในผลลัพธ์ใหม่ ซึ่งได้รับการพิสูจน์ผ่านความร่วมมือออนไลน์แบบเปิดที่เรียกว่าโครงการ Polymath

ในขณะเดียวกันอีก กระดาษที่ผ่านมา วิเคราะห์ชุดลูกเต๋าตั้งแต่สี่ลูกขึ้นไป การค้นพบนั้นอาจเป็นเรื่องที่ขัดแย้งกันมากกว่า ตัวอย่างเช่น หากคุณสุ่มเลือกลูกเต๋าสี่ลูกแล้วพบว่า A เต้น B, B เต้น C และ C เต้น Dแล้วมันเล็กน้อย ข้อมูลเพิ่มเติม น่าจะเป็น D ที่จะชนะ A กว่าด้านหลัง

ไม่แข็งแกร่งหรืออ่อนแอ

ผลลัพธ์ล่าสุดเริ่มขึ้นเมื่อประมาณทศวรรษที่แล้ว หลังจากที่คอนรีย์เข้าร่วมการชุมนุมสำหรับครูคณิตศาสตร์ด้วยเซสชันที่ครอบคลุมอกรรมกริยาลูกเต๋า “ผมไม่รู้ว่าสิ่งเหล่านี้มีอยู่จริง” เขากล่าว “ฉันรู้สึกทึ่งกับพวกเขา”

เขาตัดสินใจ (ต่อมาได้เข้าร่วมโดยเพื่อนร่วมงานของเขา เคนท์ มอร์ริสัน ที่ AIM) เพื่อสำรวจหัวข้อนี้กับนักเรียนมัธยมปลายสามคนที่เขาเป็นที่ปรึกษา ได้แก่ James Gabbard, Katie Grant และ Andrew Liu บ่อยแค่ไหนที่กลุ่มสงสัยว่าลูกเต๋าที่สุ่มเลือกจะสร้างวัฏจักรอกรรมกริยาหรือไม่?

ชุดของลูกเต๋าอกรรมกริยาถือเป็นของหายากหากหมายเลขหน้าของลูกเต๋ารวมกันเป็นผลรวมที่แตกต่างกัน เนื่องจากการตายที่มีผลรวมสูงสุดมีแนวโน้มที่จะเอาชนะลูกเต๋าอื่นๆ ทีมงานจึงตัดสินใจมุ่งเน้นไปที่ลูกเต๋าที่มีคุณสมบัติ 1 ประการ ประการแรก ลูกเต๋าใช้ตัวเลขเดียวกันกับลูกเต๋ามาตรฐาน — XNUMX ถึง nในกรณีของ n-ด้านตาย และประการที่สอง หมายเลขหน้าจะรวมกันเป็นจำนวนเดียวกันกับแม่พิมพ์มาตรฐาน แต่ไม่เหมือนลูกเต๋ามาตรฐานตรงที่ลูกเต๋าแต่ละลูกอาจออกเลขบางตัวซ้ำกันและไม่ต้องออกเลขอื่น

ในกรณีของลูกเต๋า 32 ด้าน จะมีลูกเต๋าเพียง XNUMX ลูกที่มีคุณสมบัติทั้งสองนี้ ดังนั้นด้วยความช่วยเหลือของคอมพิวเตอร์ ทีมงานจึงสามารถระบุได้ว่ามีสามตัวใดบ้าง A เต้น B และ B เต้น C. นักวิจัยค้นพบด้วยความประหลาดใจว่า A เต้น C ใน 1,756 สามเท่าและ C เต้น A ใน 1,731 สามเท่า - ตัวเลขที่เกือบจะเหมือนกัน จากการคำนวณและการจำลองลูกเต๋าที่มีมากกว่า XNUMX ด้าน ทีมคาดเดา เมื่อจำนวนด้านบนลูกเต๋าเข้าใกล้อนันต์ ความน่าจะเป็นนั้น A เต้น C เข้าใกล้ 50%

การคาดเดาที่ผสมผสานระหว่างการเข้าถึงได้ง่ายและความแตกต่างเล็กน้อยทำให้ Conrey เป็นอาหารที่ดีสำหรับโครงการ Polymath ซึ่งนักคณิตศาสตร์หลายคนมารวมตัวกันทางออนไลน์เพื่อแบ่งปันแนวคิด ในช่วงกลางปี ​​2017 เขาเสนอแนวคิดนี้ต่อ Gowers ซึ่งเป็นผู้ริเริ่มแนวทางของ Polymath “ฉันชอบคำถามนี้มาก เพราะมันมีค่าอย่างน่าประหลาดใจ” Gowers กล่าว เขาเขียน ก โพสต์บล็อก เกี่ยวกับการคาดเดาที่ดึงดูดความคิดเห็นจำนวนมาก และตลอดหกโพสต์เพิ่มเติม ผู้แสดงความคิดเห็นประสบความสำเร็จในการพิสูจน์

ในกระดาษของพวกเขา โพสต์ออนไลน์ ในปลายเดือนพฤศจิกายน พ.ศ. 2022 ส่วนสำคัญของการพิสูจน์เกี่ยวข้องกับการแสดงให้เห็นว่าส่วนใหญ่แล้ว มันไม่สมเหตุสมผลเลยที่จะพูดว่าการตายตัวเดียวนั้นแข็งแกร่งหรืออ่อนแอ ลูกเต๋าของบัฟเฟตต์ซึ่งไม่มีลูกไหนที่แข็งแกร่งที่สุดในกลุ่มนั้นไม่ใช่เรื่องผิดปกติ: หากคุณสุ่มเลือกลูกเต๋า โครงการ Polymath แสดงให้เห็น มีแนวโน้มที่จะเอาชนะลูกเต๋าอีกครึ่งหนึ่งและเสียอีกครึ่งหนึ่งไป Gowers กล่าวว่า "การตายเกือบทุกครั้งค่อนข้างธรรมดา

โปรเจ็กต์แตกต่างจากโมเดลดั้งเดิมของทีม AIM ในแง่หนึ่ง: เพื่อทำให้เทคนิคบางอย่างง่ายขึ้น โปรเจ็กต์ประกาศว่าลำดับของตัวเลขบนลูกเต๋ามีความสำคัญ ตัวอย่างเช่น 122556 และ 152562 จะถือว่าเป็นลูกเต๋าสองลูกที่ต่างกัน แต่ผลลัพธ์ของ Polymath เมื่อรวมกับหลักฐานการทดลองของทีม AIM ทำให้เกิดข้อสันนิษฐานที่ชัดเจนว่าการคาดเดานั้นเป็นจริงในแบบจำลองดั้งเดิมเช่นกัน Gowers กล่าว

“ฉันรู้สึกยินดีอย่างยิ่งที่พวกเขาได้ข้อพิสูจน์นี้ขึ้นมา” คอนรีย์กล่าว

เมื่อพูดถึงการสะสมของลูกเต๋าตั้งแต่สี่ลูกขึ้นไป ทีม AIM ได้ทำนายพฤติกรรมที่คล้ายกันกับลูกเต๋าสามลูก ตัวอย่างเช่น ถ้า A เต้น B, B เต้น C และ C เต้น D ก็น่าจะมีความเป็นไปได้ประมาณ 50-50 D เต้น Aเข้าใกล้ 50-50 อย่างแน่นอนเมื่อจำนวนด้านบนลูกเต๋าเข้าใกล้อนันต์

เพื่อทดสอบการคาดเดา นักวิจัยได้จำลองการแข่งขันแบบตัวต่อตัวสำหรับชุดลูกเต๋าสี่ลูกที่มีด้าน 50, 100, 150 และ 200 การจำลองไม่เป็นไปตามการคาดคะเนของพวกเขาค่อนข้างใกล้เคียงกับในกรณีของลูกเต๋าสามลูก แต่ก็ยังใกล้เคียงพอที่จะสนับสนุนความเชื่อของพวกเขาในการคาดเดา แม้ว่านักวิจัยจะไม่ได้ตระหนักถึงความคลาดเคลื่อนเล็กน้อยเหล่านี้มีข้อความที่แตกต่างกัน: สำหรับชุดลูกเต๋าสี่ลูกขึ้นไป การคาดเดาของพวกเขาจะเป็นเท็จ

“เราต้องการให้ [การคาดเดา] เป็นจริง เพราะมันเจ๋งมาก” คอนรีย์กล่าว

ในกรณีของลูกเต๋าสี่ลูก เอลิซาเบตต้า คอร์นาเชีย ของสถาบันเทคโนโลยีแห่งสมาพันธรัฐโลซานและ ยัน เฮซวา ของสถาบันคณิตศาสตร์วิทยาศาสตร์แห่งแอฟริกาในคิกาลี ประเทศรวันดา แสดงให้เห็นในก กระดาษ โพสต์ออนไลน์เมื่อปลายปี 2020 ว่าหาก A เต้น B, B เต้น C และ C เต้น Dแล้ว D มีโอกาสตีดีกว่า 50% เล็กน้อย A — อาจอยู่ที่ประมาณ 52% Hązłaกล่าว (เช่นเดียวกับกระดาษ Polymath Cornacchia และHązła ใช้แบบจำลองที่แตกต่างจากกระดาษ AIM เล็กน้อย)

การค้นพบของ Cornacchia และ Hązła เกิดจากข้อเท็จจริงที่ว่า แม้ว่าตามกฎแล้ว การตายเพียงครั้งเดียวจะไม่แข็งแรงหรืออ่อนแอ แต่บางครั้งลูกเต๋าคู่หนึ่งก็สามารถมีจุดแข็งร่วมกันได้ หากคุณหยิบลูกเต๋าสองลูกโดยการสุ่ม Cornacchia และ Hązła แสดงให้เห็นว่ามีความเป็นไปได้ที่ดีที่ลูกเต๋าจะสัมพันธ์กัน: พวกเขามักจะเอาชนะหรือแพ้ในลูกเต๋าลูกเดียวกัน “ถ้าฉันขอให้คุณสร้างลูกเต๋าสองลูกที่อยู่ใกล้กัน ปรากฎว่าเป็นไปได้” Hązłaกล่าว ความสัมพันธ์เล็ก ๆ น้อย ๆ เหล่านี้ทำให้ผลลัพธ์ของทัวร์นาเมนต์ห่างไกลจากความสมมาตรทันทีที่มีลูกเต๋าอย่างน้อยสี่ลูกในภาพ

เอกสารล่าสุดไม่ใช่จุดสิ้นสุดของเรื่องราว กระดาษของ Cornacchia และHązłaเริ่มที่จะเปิดเผยอย่างแม่นยำว่าความสัมพันธ์ระหว่างลูกเต๋าไม่สมดุลกับสมมาตรของทัวร์นาเมนต์อย่างไร ในระหว่างนี้ เรารู้แล้วว่าตอนนี้มีลูกเต๋าอกรรมกริยาอยู่หลายชุด บางทีอาจจะเป็นลูกที่ละเอียดพอที่จะหลอกให้บิล เกตส์เลือกก่อนก็ได้