การพิสูจน์ทางวิทยาการคอมพิวเตอร์สุดเซอร์ไพรส์ทำให้นักคณิตศาสตร์ตกตะลึง

ในวันอาทิตย์ที่ 5 กุมภาพันธ์ Olof Sisask และ Thomas Bloom ได้รับอีเมลที่มีความก้าวหน้าอันน่าทึ่งเกี่ยวกับปัญหาที่ยังไม่ได้แก้ไขที่ใหญ่ที่สุดในสายงานของพวกเขา Zander Kelley นักศึกษาระดับบัณฑิตศึกษาจาก University of Illinois, Urbana-Champaign ได้ส่ง Sisask และ Bloom กระดาษที่เขาเขียน กับ Raghu Meka แห่งมหาวิทยาลัยแคลิฟอร์เนีย ลอสแองเจลิส ทั้ง Kelley และ Meka เป็นนักวิทยาศาสตร์คอมพิวเตอร์ ซึ่งเป็นโลกทางปัญญานอกเหนือจากคอมบิเนเตอร์แบบบวกที่ Sisask และ Bloom ศึกษา

“จิตใจของฉันปลิวไปแล้ว เช่นเดี๋ยวก่อนพวกเขาทำสิ่งนี้จริง ๆ เหรอ” Sisask อาจารย์ประจำมหาวิทยาลัยสตอกโฮล์มกล่าว Kelley และ Meka บุคคลภายนอกในสาขา combinatorics กล่าวว่าพวกเขาได้พบขีดจำกัดใหม่ของขนาดของชุดของจำนวนเต็มซึ่งไม่มีสามตัวที่มีระยะห่างเท่ากัน (ตัดชุดค่าผสมอย่างเช่น 3, 8 และ 13) หรือ 101, 201 และ 301)

คำกล่าวอ้างของ Kelley และ Meka ทำลายสถิติก่อนหน้านี้ ได้สำเร็จในปี 2020 โดย Sisask และ Bloom ซึ่งเป็นนักวิจัยจากมหาวิทยาลัยอ็อกซ์ฟอร์ด “งานของ Bloom และ Sisask ซึ่งเป็นงานที่แข็งแกร่งมาก ให้ความรู้สึกว่ายากที่จะปรับปรุงให้ดีขึ้น” เบน กรีน เพื่อนร่วมงานของ Bloom ที่อ็อกซ์ฟอร์ดกล่าว “มันดูติดมากตรงที่มันอยู่”

แม้ว่าทั้ง Bloom และ Sisask จะมีเรื่องเร่งด่วนอื่นๆ ที่ต้องจัดการในเวลาที่พวกเขาได้รับอีเมล แต่ Bloom เพิ่งรับเลี้ยงลูกสุนัขตัวหนึ่ง ขณะที่ Sisask อยู่ระหว่างการย้าย พวกเขาจึงเริ่มทำงานตรวจสอบเอกสารฉบับใหม่อย่างรวดเร็ว

ภายในไม่กี่วัน Bloom และ Sisask ก็มั่นใจว่าข้อพิสูจน์ใหม่นั้นถูกต้อง Sisask เรียกมันว่า “ผลลัพธ์ที่ใหญ่ที่สุดในพื้นที่เป็นเวลา 20 ปี” ต้องการให้ผู้อื่นชื่นชมความคิดของ Kelley และ Meka พวกเขาร่างขึ้น เพื่อรายงาน อธิบายการพิสูจน์ในแง่ที่นักคณิตศาสตร์คุ้นเคยมากกว่า

Meka กล่าวว่าการตอบรับจากชุมชนนั้น “เป็นไปในเชิงบวกมากกว่าที่ฉันคิดไว้ มันวิเศษมากที่ได้เห็นข้อเสนอแนะทั้งหมด”

ความคืบหน้ายืดเยื้อ

ลำดับของตัวเลขที่มีระยะห่างเท่าๆ กันที่ Kelley และ Meka พยายามหลีกเลี่ยงเรียกว่า ลำดับขั้นทางคณิตศาสตร์ พวกเขาสามารถคงอยู่ตลอดไปหรือมีเพียงไม่กี่คำ Kelley และ Meka จดจ่อกับความก้าวหน้าที่ประกอบด้วยตัวเลขเพียงสามตัว ตามสายการวิจัยที่มักโยงไปถึง กระดาษ 1936 โดย Paul Erdős และ Paul Turán

Erdős และ Turán ต้องการทราบว่ามีกี่ตัวเลขที่เล็กกว่าเพดานบางส่วน N สามารถใส่ลงในชุดโดยไม่ต้องสร้างความก้าวหน้าทางเลขคณิตสามเทอม N อาจเป็น 1,000, 1 ล้าน หรือตัวเลขที่มากเกินจินตนาการ พวกเขาคาดเดาว่าเป็น N มีขนาดใหญ่ขึ้น ชุดที่ไม่มีความก้าวหน้าสามระยะจะต้องเบาบางอย่างไม่น่าเชื่อ การสร้างชุดดังกล่าวก็เหมือนกับการสะสมรองเท้าโดยยืนยันว่าไม่มีคู่ใดคู่หนึ่งที่มีสีเดียวกัน บางทีคุณอาจทำต่อไปได้ตลอดไป แต่เมื่อคอลเล็กชันของคุณมีขนาดใหญ่ขึ้น คุณจะพบว่าตัวเองกำลังเพิ่มมันในอัตราที่ช้าลงและช้าลง

“มีโครงสร้างบางอย่างที่จะโผล่เข้ามาในฉาก ไม่ว่าคุณจะเลือกฉากนั้นอย่างไร” เมก้าอธิบาย “คุณต้องการชุดขนาดใหญ่แค่ไหนจึงจะรับประกันได้ว่าคุณมีโครงสร้างนี้อยู่ในนั้น”

ในปี 1946 เฟลิกซ์ เบห์เรนด์ พบวิธีสร้างชุด ของตัวเลขระหว่าง 1 ถึง N โดยไม่ทำให้เกิดความก้าวหน้าสามระยะ วิธีการของเขาส่งผลให้ชุดใหญ่ขึ้นตาม N ทำได้ แต่เจ็บอย่างช้าๆ เมื่อไร N คือ 100,000 ชุดของ Behrend มีเพียง 171 องค์ประกอบ เมื่อไร N คือ 1 ล้าน ชุดของเขามี 586 หมายเลข ซึ่งน้อยกว่า 0.06% ของตัวเลขระหว่าง 1 ถึง 1 ล้าน

เซตของ Behrend ช่วยให้นักคณิตศาสตร์มีพื้นในการทำงาน: เซตที่ใหญ่ที่สุดที่ไม่มีความก้าวหน้าสามระยะจะต้องมีขนาดใหญ่เท่ากับของ Behrend เป็นอย่างน้อย ในปี 1953 เคลาส์ รอธ จัดให้มีฝ้าเพดานการค้นหาเกณฑ์ที่ผ่านมาซึ่งชุดจะต้องมีความก้าวหน้าสามระยะอย่างหลีกเลี่ยงไม่ได้

Roth ได้พิสูจน์การคาดเดาของ Erdős และ Turán โดยแสดงให้เห็นว่าเป็น N ยิ่งใหญ่ขึ้น ชุดที่ไม่มีความก้าวหน้าสามระยะจะประกอบด้วยเศษส่วนที่เล็กกว่าของตัวเลขระหว่าง 1 ถึง N แต่เพดานของ Roth นั้นอยู่ไกลจากพื้นของ Behrend Behrend แสดงให้เห็นว่า 0.06% ขององค์ประกอบระหว่าง 1 ถึง 1 ล้านสามารถใส่ลงในชุดที่ไม่มีความก้าวหน้าได้ แม้ว่าสูตรของ Roth จะคำนวณได้อย่างแม่นยำได้ยาก แต่ก็ไม่มีที่ไหนเลยที่ต่ำขนาดนั้น การประมาณอย่างคร่าว ๆ ครั้งหนึ่งได้กำหนดเปอร์เซ็นต์ไว้ที่ประมาณ 40%

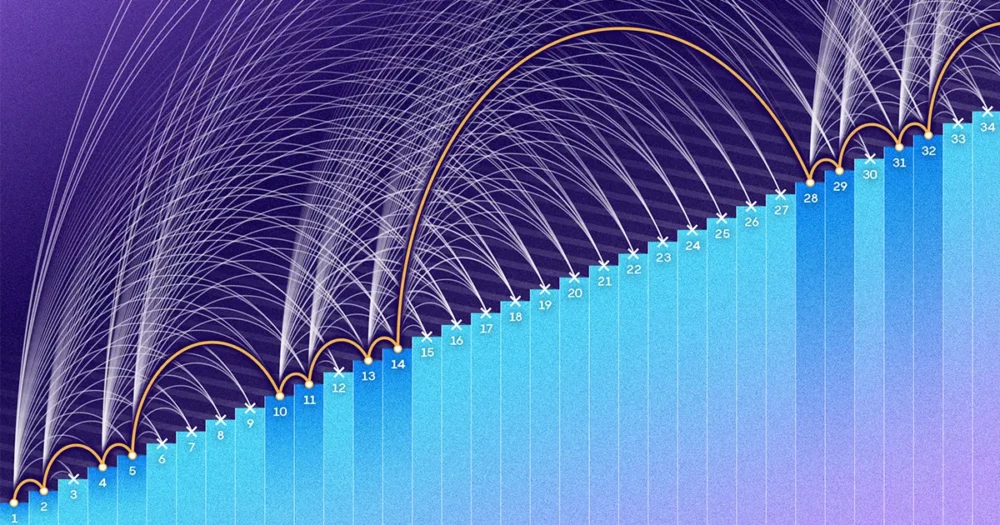
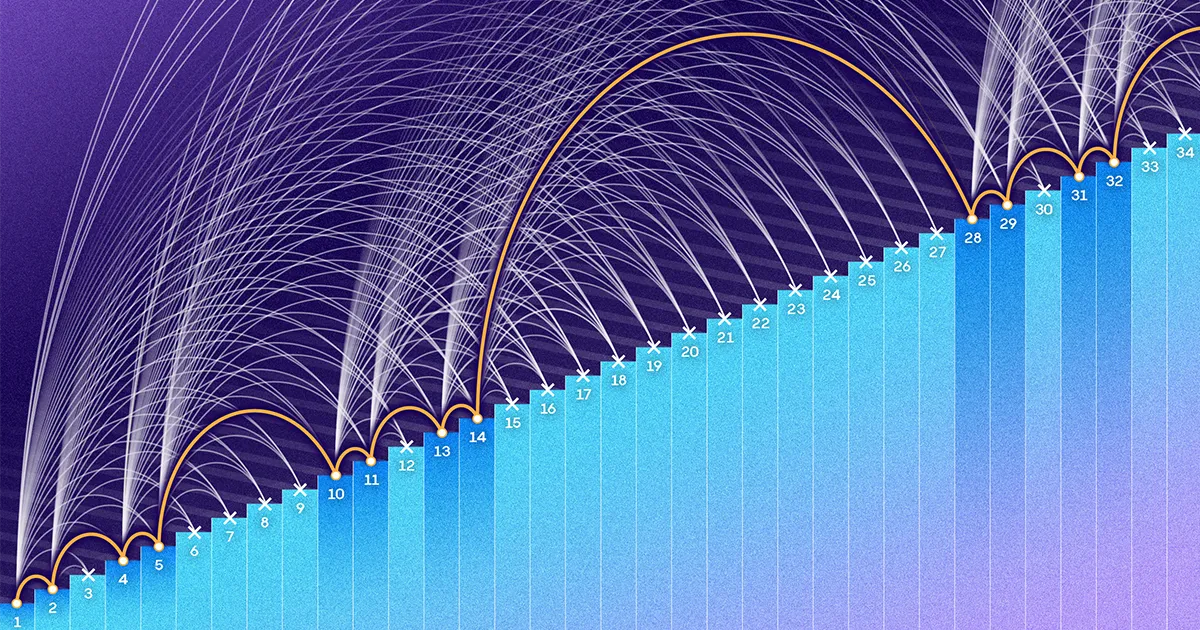
แต่ที่โดดเด่นกว่าช่องว่างนั้นคือพฤติกรรมโดยรวมของทั้งสองสูตร พล็อตเศษส่วนขององค์ประกอบระหว่าง 1 และ N ที่แต่ละสูตรเป็นตัวแทน และคุณจะเห็นจำนวนของ Behrend ลดลงอย่างรวดเร็วจนเหลือศูนย์เป็น N เติบโตขึ้น ในทางกลับกัน เศษส่วนของ Roth เลื่อนเข้าหาศูนย์ แต่อย่างช้าๆ และนุ่มนวล เส้นโค้งสองเส้นมีรูปร่างที่แตกต่างกันมาก และสัดส่วนที่แท้จริงขององค์ประกอบที่อยู่ในเซตที่ไม่มีความก้าวหน้าทางเลขคณิตอาจอยู่ที่ใดก็ได้ระหว่างเส้นโค้งทั้งสองเท่าที่นักคณิตศาสตร์ทราบ

เริ่มต้นในทศวรรษที่ 1980 “มีลำดับที่ยาวนานของการเข้าใจถึงปัญหาหลังเหตุการณ์ การปรับปรุงที่เพิ่มขึ้นค่อนข้างมากโดยนักคณิตศาสตร์ที่มีชื่อเสียงจริงๆ จำนวนมาก” กรีนกล่าว นานๆ ครั้ง จะมีคนเขยิบขีดจำกัดบนของ Roth ลงมาด้วยผมเส้นหนึ่งหรือสองเส้น และในที่สุดมันก็ลดระดับลงมาก ตรงกันข้าม ขอบเขตล่างของ Behrend ไม่ขยับเขยื้อนมานานหลายทศวรรษ นักคณิตศาสตร์เริ่มคิดว่า Behrend อาจอยู่ไม่ไกลจากคำตอบที่แท้จริง Bloom กล่าว

จนกระทั่งเอกสารของ Kelley และ Meka มาถึงในต้นปี 2023 ขนาดสูงสุดของชุดที่ไม่มีความก้าวหน้าถูกเขียนจากด้านล่างโดยสูตรของ Behrend และจากด้านบนโดย Bloom และ Sisask's เอกสารของ Bloom และ Sisask ในเดือนกรกฎาคม 2020 ได้ข้ามเกณฑ์ "ลอการิทึม" ที่สำคัญ โดยแสดงให้เห็นว่าเซตที่ปราศจากความก้าวหน้าจะต้องมีค่าน้อยกว่าอย่างมาก N/(บันทึก N) องค์ประกอบ แต่ผลลัพธ์ของพวกเขายังคงสูงเหนือ Behrend's ขอบเขตบนใหม่ของ Kelley และ Meka นั้นใกล้กับพื้นที่กำหนดโดย Behrend อย่างมาก

“Meka และ Kelley มีความก้าวหน้าแบบก้าวกระโดดทั้งหมดนี้” Terence Tao นักคณิตศาสตร์ผู้มีชื่อเสียงแห่ง UCLA กล่าว

สูตรของพวกเขาเกือบจะเหมือนกับของ Behrend โดยมีการปรับแต่งพารามิเตอร์เพียงเล็กน้อยเท่านั้น เช่น N เข้าใกล้อนันต์ พล็อตของสูตรของ Kelley และ Meka จะกลายเป็นเส้นโค้งที่คล้ายกับเส้นโค้ง Behrend ในที่สุด “การผูกมัดของรูปร่างนั้นดูเหมือนเป็นความฝันที่เป็นไปไม่ได้มาก่อน” บลูมกล่าว

“ฉันค่อนข้างเซจริงๆ ที่พวกเขาทำการปรับปรุงเช่นนี้” กรีนกล่าว

แทคที่แตกต่าง

 แม้ว่า Kelley และ Meka จะไม่เคยทำการวิจัยทางคณิตศาสตร์มาก่อนอย่างเต็มที่ แต่ความก้าวหน้าทางเลขคณิตเป็นสิ่งที่คุ้นเคยสำหรับพวกเขาเมื่อพวกเขาเริ่มต้น โดยทั่วไปแล้ว นักวิทยาศาสตร์คอมพิวเตอร์ “กำลังมองหาเทคนิคที่จะแก้ปัญหาของเราอย่างหิวกระหาย” Kelley กล่าว เครื่องมือในอดีตที่ใช้ในการศึกษาขนาดของชุดที่ไม่มีความก้าวหน้าได้ถูกนำมาใช้อย่างแพร่หลายในสาขาย่อยของวิทยาการคอมพิวเตอร์ของทฤษฎีความซับซ้อน ปัญหาของการจำกัดขนาดของชุดดังกล่าวเป็นที่รู้จักกันดีสำหรับนักทฤษฎีความซับซ้อนว่าเป็นตัวอย่างที่เป็นแก่นสารของการใช้เทคนิคที่ตรวจสอบโครงสร้างภายในของชุด

ในช่วงปลายปี 2021 Kelley และ Meka กำลังวิเคราะห์โอกาสที่ทีมผู้เล่นในเกมที่ร่วมมือกันจะสามารถชนะได้ ซึ่งเป็นปัญหามาตรฐานของวิทยาการคอมพิวเตอร์ พวกเขาคิดว่าเทคนิคจากการวิจัยเกี่ยวกับขนาดของชุดที่ไม่มีความก้าวหน้าอาจเป็นประโยชน์ แต่พวกเขาพบว่าง่ายกว่าที่จะศึกษาเทคนิคเหล่านั้นโดยตรงมากกว่านำไปใช้กับเกมแบบร่วมมือ Kelley กล่าวว่า "ความคิดที่ดีที่สุดของฉันเกี่ยวกับวิธีแก้ไขปัญหานี้ [คือ] การปรับปรุงตัวเครื่องมือจริงๆ ไม่ใช่การใช้อย่างฉลาดกว่านี้" Kelley กล่าว

“ในจุดหนึ่ง เราเพิ่งตัดสินใจที่จะทำงานเกี่ยวกับคำถามนี้โดยตรง” Meka เล่า หกเดือนต่อมา นักวิจัยทั้งสองได้ค้นพบกลยุทธ์ของพวกเขา และเพียงแค่ต้องหาวิธีนำวิธีการนี้ไปใช้กับปัญหาที่มีอยู่

หากต้องการดูว่าพวกเขามาถึงขีดจำกัดบนใหม่ได้อย่างไร ให้ใช้ชุดตัวเลขใดๆ ระหว่าง 1 ถึง N. โทรเลย A. ความหนาแน่นของ A คือเปอร์เซ็นต์ของตัวเลขระหว่าง 1 ถึง N ซึ่งรวมถึง เนื่องจากมีความก้าวหน้าทางคณิตศาสตร์ที่เป็นไปได้มากมายระหว่าง 1 ถึง Nถ้าคุณไม่เลือกองค์ประกอบของ A อย่างระมัดระวังใด ๆ A ที่มีความหนาแน่นสูงจะมีความก้าวหน้าทางเลขคณิตมากมาย

ในการพิสูจน์ของพวกเขา Kelley และ Meka จินตนาการว่า A มีความก้าวหน้าทางเลขคณิตน้อยหรือไม่มีเลย และพวกเขาพยายามติดตามผลลัพธ์ที่ตามมา ถ้า A มีความหนาแน่นเพียงพอ พวกเขาแสดงให้เห็นว่าการไม่มีความก้าวหน้าจำเป็นต้องมีระดับของโครงสร้างภายใน A ย่อมส่งผลให้เกิดความขัดแย้ง หมายความว่า A ต้องมีความก้าวหน้าอย่างน้อยหนึ่งรายการ

เพื่อทำความเข้าใจโครงสร้างดังกล่าว พวกเขาพิจารณาชุด A + Aซึ่งประกอบด้วยตัวเลขทั้งหมดที่เกิดจากการบวกสององค์ประกอบของ A. พวกเขาสังเกตเห็นว่าถ้า A มีความก้าวหน้าทางคณิตศาสตร์ค่อนข้างน้อย ซึ่งแสดงถึงความซ้ำซ้อนในองค์ประกอบของ A + A: คู่เลขต่างๆ จาก A มักจะรวมกันเป็นจำนวนเดียวกัน

ความหนาแน่นสามารถกำหนดได้ไม่เฉพาะเมื่อเปรียบเทียบกับจำนวนเต็มทั้งหมดระหว่าง 1 ถึง N แต่เมื่อเปรียบเทียบกับเซตย่อยบางเซต ให้พูดเฉพาะจำนวนเต็มคู่ในช่วงเวลานั้น หรือเฉพาะจำนวนทวีคูณของ 3 Kelley และ Meka ใช้ความซ้ำซ้อนใน A + A เพื่อหาเซตย่อยของจำนวนเต็มที่มีองค์ประกอบของ A เป็นเรื่องธรรมดาโดยเฉพาะ

หาก A มีจำนวนทวีคูณของ 3 มากเกินสัดส่วน เช่น Kelley และ Meka จะมุ่งความสนใจไปที่ส่วนที่มีจำนวนทวีคูณของ 3 พวกเขาใช้กลยุทธ์นี้ซ้ำแล้วซ้ำอีก ทุกครั้งที่พบชุดย่อยของจำนวนเต็มซึ่งมีขนาดเล็กลงเรื่อยๆ Aความหนาแน่นของมันจะเติบโตและเติบโตต่อไป ตัวอย่างเช่น, A อาจมี 10% ของจำนวนเต็มระหว่าง 1 ถึง N, 15% ของผลคูณของ 3 ในช่วงนั้น และ 25% ของผลคูณของ 3 คู่

สิ่งที่น่าสนใจเกิดขึ้นเมื่อ A มีขนาดใหญ่ หากทำซ้ำขั้นตอนนี้ความหนาแน่นของ A ส่วนย่อยบางส่วนเกิน 100% แน่นอนว่ามันเป็นไปไม่ได้ A อาจประกอบด้วยผลคูณทั้งหมดของ 24 แต่ไม่สามารถมีมากกว่าทั้งหมด ความขัดแย้งนี้จะเกิดขึ้นก็ต่อเมื่อ A ใหญ่พอที่จะเริ่มต้น แต่เมื่อมันเกิดขึ้นก็หมายถึงข้อสันนิษฐานว่า A ไม่มีความก้าวหน้าทางคณิตศาสตร์ใด ๆ ต้องผิด

มันเป็น "การโต้แย้งแบบ win-win" เมื่อ A เมก้ากล่าว ทั้ง A รวมถึงความก้าวหน้าทางเลขคณิตจำนวนมากหรือมีความซ้ำซ้อนมากมาย A + A — ในกรณีนี้ พวกเขาสามารถใช้ขั้นตอนการค้นหาเซ็ตย่อย (เรียกว่า “กลยุทธ์การเพิ่มความหนาแน่น”) เพื่อแสดงว่าความก้าวหน้าจะต้องปรากฏใน A. แม้ว่ากลยุทธ์การเพิ่มความหนาแน่นจะเป็นพิมพ์เขียวที่ใช้งานได้ดีในภาคสนาม แต่ Kelley และ Meka ก็สามารถทำให้มันใช้งานได้สำหรับพื้นที่ขนาดเล็ก Aกว่าที่เคยเป็นมา ด้วยเหตุนี้ พวกเขาจึงค้นพบเพดานใหม่สำหรับขนาดของฉากที่ปราศจากความก้าวหน้า

Kelley และ Meka สร้างการผสมผสานแนวคิดที่ไม่เหมือนใครจากพิมพ์เขียวการเพิ่มความหนาแน่น แทนที่จะคิดเฟรมเวิร์กใหม่ พวกเขาคิดใหม่ถึงวิธีการหาส่วนย่อยที่หนาแน่น สำหรับสิ่งนี้ พวกเขาใช้เทคนิคที่เรียกว่า "การลอด" ซึ่งประกอบด้วยการเลื่อนชุดตามจำนวนคงที่ ตัดกับตัวมันเอง และทำกระบวนการซ้ำหลายๆ ครั้ง สิ่งที่เหลืออยู่หลังจากการตัดกันหลายรอบคือชุดที่มีโครงสร้างสูงพร้อมคุณสมบัติที่คาดเดาได้ แม้ว่าเอกสารอื่น ๆ จะใช้การกรอง แต่ก็ไม่เคยมีการทดลองกับปัญหาความก้าวหน้าสามระยะ

มองย้อนกลับไป

Kelley และ Meka ดึงขีดจำกัดขนาดของชุดที่ปราศจากความก้าวหน้าลงด้วยจำนวนที่น่าตกใจโดยการใส่เครื่องมือที่ถูกละเลย เช่น การกรองเข้าไปในวิธีการดั้งเดิม “Kelley และ Meka แสดงให้เราเห็นว่าเทคนิคเหล่านี้ซึ่งนั่งอยู่กลางแจ้งนั้นมีประสิทธิภาพมากกว่าที่เราคิดไว้มาก” Bloom กล่าว ในแง่ของประสิทธิภาพที่เพิ่งค้นพบของเครื่องมือเหล่านี้ เขากล่าวเสริมว่า “เราต้องกลับไปทบทวนทุกอย่างอีกครั้ง”

กลยุทธ์การเพิ่มความหนาแน่นปรากฏขึ้นครั้งแรกในกระดาษของ Roth เมื่อ 70 ปีก่อน และถูกนำมาใช้ในเอกสารส่วนใหญ่เกี่ยวกับความก้าวหน้าทางเลขคณิตตั้งแต่นั้นเป็นต้นมา กรีนรู้สึกประหลาดใจที่สามารถใช้เฟรมเวิร์กเพื่อพิสูจน์ขอบเขตที่ต่ำพอๆ กับของ Kelley และ Meka “ผมคิดว่าต้องมีบางอย่างที่แตกต่างไปจากเดิมอย่างสิ้นเชิง” เขากล่าว

Kelley รู้สึกตื่นเต้นที่จะได้เข้าสู่วิชาคณิตศาสตร์ต่อไป “ผมไม่มีความหวังและความฝันเกี่ยวกับปัญหาต่างๆ มากมาย ซึ่งผมถือว่าอย่างน้อยก็เกี่ยวข้องกับเรื่องนี้ทางจิตวิญญาณ” เขากล่าว

การที่ Kelley และ Meka สามารถมองเห็นจุดแข็งของแนวคิดที่ครั้งหนึ่งเคยถูกมองข้ามได้นั้น แสดงให้เห็นถึงธรรมชาติของความก้าวหน้าทางคณิตศาสตร์ที่มักเหมาะสม — คุณสมบัติที่ Tao มอบให้นั้นถือเป็นพรมากกว่าคำสาป “ไม่เสมอไปที่คณิตศาสตร์จะยากขึ้นเรื่อย ๆ และยากขึ้นเรื่อย ๆ” เขากล่าว "ขอบคุณพระเจ้า."