Python Örnekleriyle Big O Notasyonu ve Algoritma Analizi

Giriş

Bir bilgisayar programı kullanarak sorunu çözmenin genellikle birden çok yolu vardır. Örneğin, bir dizideki öğeleri sıralamanın birkaç yolu vardır. birleştirme sırası, kabarcık sıralaması, ekleme türü, ve benzeri. Bu algoritmaların hepsinin kendi artıları ve eksileri vardır ve geliştiricinin işi, herhangi bir kullanım durumunda kullanılacak en iyi algoritmayı seçebilmek için onları tartmaktır. Başka bir deyişle, asıl soru, soruna birden fazla çözüm olduğunda belirli bir sorunu çözmek için hangi algoritmanın kullanılacağıdır.

algoritma analizi farklı algoritmaların karmaşıklığının analizini ve eldeki sorunu çözmek için en verimli algoritmayı bulmayı ifade eder. Big-O gösterimi algoritmanın karmaşıklığını tanımlamak için kullanılan istatistiksel bir ölçüdür.

Bu kılavuzda, önce algoritma analizinin kısa bir incelemesini yapacağız ve ardından Big-O notasyonuna daha derinlemesine bakacağız. Big-O notasyonunun farklı Python fonksiyonlarının yardımıyla algoritma karmaşıklığını bulmak için nasıl kullanılabileceğini göreceğiz.

Algoritma Analizi Neden Önemlidir?

Algoritma analizinin neden önemli olduğunu anlamak için basit bir örnekten yardım alacağız. Bir yöneticinin, iki çalışanına, Python'da, kullanıcı tarafından girilen bir sayının faktöriyelini hesaplayan bir algoritma tasarlama görevi verdiğini varsayalım. İlk çalışan tarafından geliştirilen algoritma şöyle görünür:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Algoritmanın argüman olarak bir tamsayı aldığına dikkat edin. İçinde fact() adlı bir değişkeni işle product başlatıldı 1. Bir döngü yürütülür 1 için n ve her yineleme sırasında, product döngü tarafından yinelenen sayı ile çarpılır ve sonuç product yine değişken. Döngü yürütüldükten sonra, product değişken faktöriyel içerecektir.

Benzer şekilde, ikinci çalışan da bir sayının faktöriyelini hesaplayan bir algoritma geliştirdi. İkinci çalışan, sayının faktöriyelini hesaplamak için özyinelemeli bir işlev kullandı. n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Yönetici hangi algoritmayı kullanacağına karar vermelidir. Bunu yapmak için hangi algoritmanın daha hızlı çalıştığını seçmeye karar verdiler. Bunu yapmanın bir yolu, aynı girişte kodu yürütmek için gereken süreyi bulmaktır.

Jupyter not defterinde şunları kullanabilirsiniz: %timeit literal ve ardından fonksiyonun yürütülmesi için geçen süreyi bulmak için fonksiyon çağrısı:

%timeit fact(50)

Bu bize şunları verecektir:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Çıktı, algoritmanın aldığını söylüyor 9 mikrosaniye (artı/eksi 45 nanosaniye) döngü başına.

Benzer şekilde, ikinci yaklaşımın uygulanmasının ne kadar zaman alacağını hesaplayabiliriz:

%timeit fact2(50)

Bunun sonucu:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Özyinelemeyi içeren ikinci algoritma, 15 mikrosaniye (artı/eksi 427 nanosaniye).

Yürütme süresi, birinci algoritmanın özyineleme içeren ikinci algoritmaya kıyasla daha hızlı olduğunu göstermektedir. Büyük girdilerle uğraşırken performans farkı daha önemli hale gelebilir.

Ancak yürütme süresi, donanıma bağlı olduğundan bir algoritmanın karmaşıklığını ölçmek için iyi bir ölçüm değildir. Bir algoritma için daha nesnel bir karmaşıklık analizi metriği gereklidir. Burası Büyük O gösterimi oynamaya geliyor.

Big-O Notasyonu ile Algoritma Analizi

Big-O notasyonu, algoritmaya giriş ile algoritmayı yürütmek için gereken adımlar arasındaki ilişkiyi belirtir. Büyük bir "O" ile gösterilir, ardından bir açma ve kapama parantezleri gelir. Parantez içinde girdi ile algoritmanın attığı adımlar arasındaki ilişki “n” ile gösterilir.

Anahtar paket servisi şudur: Big-O, bir belirli gibi bir algoritma çalıştırdığınız örnek fact(50), daha doğrusu, ne kadar iyi ölçek artan girdi verilir. Bu, değerlendirme için somut bir örnek için somut zamandan çok daha iyi bir ölçümdür!

Örneğin, eğer bir Doğrusal ilişki Girdi ile algoritmanın yürütmesini tamamlamak için attığı adım arasında, kullanılan Big-O notasyonu olacaktır. O (n). Benzer şekilde, Big-O notasyonu için ikinci dereceden fonksiyonlar is O(n²).

Sezgi oluşturmak için:

• O (n): içinde n=1, 1 adım atılır. saat n=10, 10 adım atılır.
• O(n²): içinde n=1, 1 adım atılır. saat n=10, 100 adım atılır.

At n=1, bu ikisi aynı şeyi yapacaktı! Bu, girdi ile bu girdiyi işlemek için gereken adım sayısı arasındaki ilişkiyi gözlemlemenin, bazı somut girdilerle fonksiyonları değerlendirmekten daha iyi olmasının bir başka nedenidir.

Aşağıdakiler en yaygın Big-O işlevlerinden bazılarıdır:

Name	Büyük o
sabit	O (c)
doğrusal	O (n)
ikinci dereceden	O(n²)
Kübik	O(n³)
Üstel	Ç(2ⁿ)
Logaritmik	O (günlük (n))
Günlük Doğrusal	Ç(nlog(n))

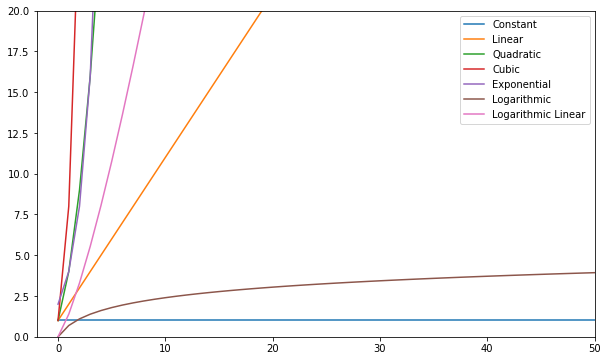
Bu işlevleri görselleştirebilir ve karşılaştırabilirsiniz:

Genel olarak konuşursak – doğrusaldan daha kötü olan her şey kötü bir karmaşıklık (yani verimsiz) olarak kabul edilir ve mümkünse bundan kaçınılmalıdır. Doğrusal karmaşıklık iyidir ve genellikle gerekli bir kötülüktür. Logaritmik iyidir. Sabit harika!

Bir Big-O'nun nasıl hesaplandığı hakkında bir fikir edinmek için, bazı sabit, doğrusal ve ikinci dereceden karmaşıklık örneklerine bir göz atalım.

Sabit Karmaşıklık – Ç(C)

Bir algoritmanın yürütülmesini tamamlamak için gereken adımlar, girdi sayısından bağımsız olarak sabit kalırsa, bir algoritmanın karmaşıklığının sabit olduğu söylenir. Sabit karmaşıklık ile gösterilir O (c) nerede c herhangi bir sabit sayı olabilir.

Listedeki ilk öğenin karesini bulan ve ardından ekrana yazdıran Python'da basit bir algoritma yazalım:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

Yukarıdaki komut dosyasında, giriş boyutundan bağımsız olarakveya giriş listesindeki öğelerin sayısı items, algoritma yalnızca 2 adım gerçekleştirir:

1. İlk elemanın karesini bulma
2. Sonucu ekrana yazdırma.

Bu nedenle, karmaşıklık sabit kalır.

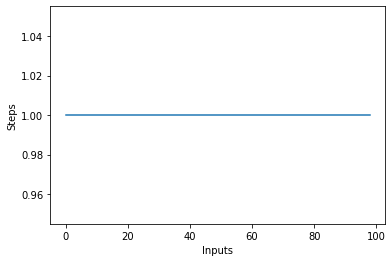
Değişken boyutta bir çizgi grafiği çizerseniz, items X ekseninde girdi ve Y ekseninde adım sayısı, düz bir çizgi elde edeceksiniz. Bunu görselleştirmemize yardımcı olacak kısa bir komut dosyası oluşturalım. Giriş sayısı ne olursa olsun, yürütülen adımların sayısı aynı kalır:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Doğrusal Karmaşıklık – O (n)

Bir algoritmanın yürütülmesini tamamlamak için gereken adımlar, girdi sayısı ile doğrusal olarak artar veya azalırsa, bir algoritmanın karmaşıklığının doğrusal olduğu söylenir. Doğrusal karmaşıklık ile gösterilir O (n).

Bu örnekte, listedeki tüm öğeleri konsola görüntüleyen basit bir program yazalım:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Karmaşıklığı linear_algo() for döngüsünün yineleme sayısı girişin boyutuna eşit items dizi. Örneğin, 4 öğe varsa items liste, for döngüsü 4 kez yürütülecektir.

X eksenindeki giriş sayısı ve y eksenindeki adım sayısı ile doğrusal karmaşıklık algoritması için hızlı bir şekilde bir çizim oluşturalım:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Bunun sonucu:

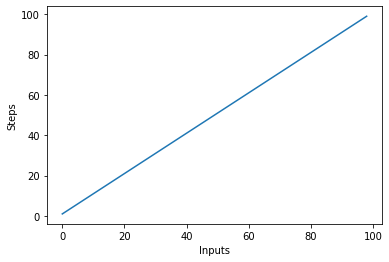
Unutulmaması gereken önemli bir nokta, büyük girdilerde sabitlerin değer kaybetme eğiliminde olmasıdır. Bu nedenle, genellikle Big-O notasyonundan sabitleri kaldırırız ve O(2n) gibi bir ifade genellikle O(n) olarak kısaltılır. Hem O(2n) hem de O(n) doğrusaldır - önemli olan somut değer değil, doğrusal ilişkidir. Örneğin, modifiye edelim linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Girdi üzerinde yinelenen iki for döngüsü vardır. items liste. Bu nedenle algoritmanın karmaşıklığı O (2n), ancak giriş listesinde sonsuz öğe olması durumunda, sonsuzun iki katı hala sonsuzluğa eşittir. Sabiti görmezden gelebiliriz 2 (nihai olarak önemsiz olduğu için) ve algoritmanın karmaşıklığı kalır O (n).

X eksenindeki girdileri ve Y eksenindeki adım sayısını çizerek bu yeni algoritmayı görselleştirelim:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Yukarıdaki komut dosyasında bunu açıkça görebilirsiniz. y=2n, ancak çıktı doğrusaldır ve şöyle görünür:

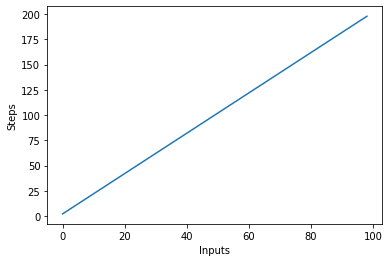
İkinci Dereceden Karmaşıklık – O(n²)

Bir algoritmayı yürütmek için gereken adımlar, girdideki öğe sayısının ikinci dereceden bir işlevi olduğunda, bir algoritmanın karmaşıklığının ikinci dereceden olduğu söylenir. İkinci dereceden karmaşıklık şu şekilde gösterilir: O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Giriş listesindeki tüm öğeleri yineleyen bir dış döngümüz ve ardından giriş listesindeki tüm öğeleri yineleyen iç içe geçmiş bir iç döngümüz var. Gerçekleştirilen toplam adım sayısı n*n'dir; burada n, giriş dizisindeki öğelerin sayısıdır.

Aşağıdaki grafik, ikinci dereceden karmaşıklığa sahip bir algoritmanın adımlarına karşı girdi sayısını göstermektedir:

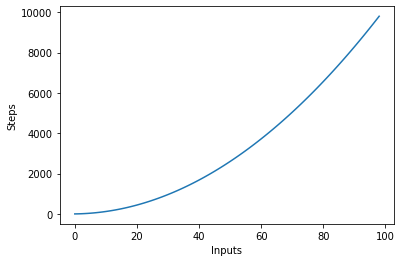
Logaritmik Karmaşıklık – O (logn)

Bazı algoritmalar, örneğin logaritmik karmaşıklığa ulaşır. Ikili arama. İkili Arama, aşağıdakileri kontrol ederek dizideki bir öğeyi arar. orta bir dizi ve öğenin olmadığı yarısını budama. Kalan yarısı için bunu tekrar yapar ve eleman bulunana kadar aynı adımlara devam eder. Her adımda, yarıları dizideki eleman sayısı.

Bu, dizinin sıralanmasını ve veriler hakkında bir varsayımda bulunmamızı gerektirir (sıralanmış gibi).

Gelen veriler hakkında varsayımlarda bulunabildiğiniz zaman, bir algoritmanın karmaşıklığını azaltan adımlar atabilirsiniz. Logaritmik karmaşıklık, yüksek düzeyde ölçeklendirilmiş girdilerle bile iyi bir performans elde ettiği için arzu edilir.

Karmaşık Fonksiyonların Karmaşıklığını Bulma?

Önceki örneklerde, girdi üzerinde oldukça basit fonksiyonlarımız vardı. Yine de, girdideki (birden çok) diğer işlevleri çağıran işlevlerin Big-O'sunu nasıl hesaplarız?

Bir göz atalım:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

Yukarıdaki komut dosyasında birkaç görev gerçekleştirilmektedir, ilk olarak, konsolda 5 kez bir dize yazdırılır. print Beyan. Ardından, giriş listesini ekrana iki kez yazdırıyoruz ve son olarak konsolda üç kez başka bir dize yazdırıyoruz. Böyle bir algoritmanın karmaşıklığını bulmak için, algoritma kodunu parçalara ayırmamız ve tek tek parçaların karmaşıklığını bulmaya çalışmamız gerekir. Her parçanın karmaşıklığını işaretleyin.

İlk bölümde elimizde:

for i in range(5):
	print("Python is awesome")

Bu bölümün karmaşıklığı O (5) girdiden bağımsız olarak bu kod parçasında beş sabit adım gerçekleştirildiğinden.

Sonra, elimizde:

for item in items:
	print(item)

Yukarıdaki kod parçasının karmaşıklığının O (n). Benzer şekilde, aşağıdaki kod parçasının karmaşıklığı da O (n):

for item in items:
	print(item)

Son olarak, aşağıdaki kod parçasında, bir dize üç kez yazdırılır, dolayısıyla karmaşıklık şu şekildedir: O (3):

print("Big O")
print("Big O")
print("Big O")

Genel karmaşıklığı bulmak için, şu bireysel karmaşıklıkları eklememiz yeterlidir:

O(5) + O(n) + O(n) + O(3)

Yukarıdakileri basitleştirerek şunları elde ederiz:

O(8) + O(2n) = O(8+2n)

Daha önce, (bu durumda uzunluğu n olan) girdi aşırı derecede büyüdüğünde, sabitlerin önemsiz hale geldiğini, yani sonsuzun iki katı veya yarısının hala sonsuz kaldığını söylemiştik. Bu nedenle sabitleri göz ardı edebiliriz. Algoritmanın son karmaşıklığı O (n)!

En Kötü ve En İyi Vaka Karmaşıklığı

Genellikle biri size bir algoritmanın karmaşıklığını sorduğunda – en kötü durum karmaşıklığıyla (Big-O) ilgilenirler. Bazen en iyi durum karmaşıklığıyla da ilgilenebilirler (Big-Omega).

Bunlar arasındaki ilişkiyi anlamak için başka bir kod parçasına bakalım:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

Yukarıdaki komut dosyasında, girdi olarak bir sayı ve bir sayı listesi alan bir fonksiyonumuz var. Girilen sayı, sayı listesinde bulunursa true, aksi takdirde döner None. Listede 2'yi ararsanız, ilk karşılaştırmada bulunur. Bu, aranan öğenin ilk aranan dizinde bulunması bakımından algoritmanın en iyi durum karmaşıklığıdır. En iyi durum karmaşıklığı, bu durumda, O (1). Öte yandan, 10'u ararsanız, son aranan dizinde bulunur. Algoritmanın listedeki tüm öğeleri araması gerekecek, dolayısıyla en kötü durum karmaşıklığı olur O (n).

En iyi ve en kötü durum karmaşıklığına ek olarak şunları da hesaplayabilirsiniz: ortalama karmaşıklık (Big-Theta) size “rastgele bir girdi verildiğinde, algoritmanın beklenen zaman karmaşıklığı nedir” diyen bir algoritmanın?

Uzay Karmaşıklığı

Bir algoritmanın yürütülmesini tamamlamak için gereken adım sayısını saydığınız zaman karmaşıklığına ek olarak, aşağıdakileri de bulabilirsiniz. alan karmaşıklığı Bu, bir programın yürütülmesi sırasında bellekte ayırmanız gereken alan miktarını ifade eder.

Aşağıdaki örneğe bir göz atın:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

The return_squares() işlev bir tamsayı listesi kabul eder ve karşılık gelen karelerle bir liste döndürür. Algoritma, giriş listesindekiyle aynı sayıda öğe için bellek ayırmak zorundadır. Bu nedenle, algoritmanın uzay karmaşıklığı O (n).

Sonuç

Big-O notasyonu, bir algoritmanın karmaşıklığını ölçmek için kullanılan standart metriktir. Bu kılavuzda, Big-O gösteriminin ne olduğunu ve çeşitli algoritmaların karmaşıklığını ölçmek için nasıl kullanılabileceğini inceledik. Ayrıca farklı Python örneklerinin yardımıyla farklı Big-O fonksiyon türlerini de inceledik. Son olarak, uzay karmaşıklığı ile birlikte en kötü ve en iyi durum karmaşıklığını kısaca gözden geçirdik.