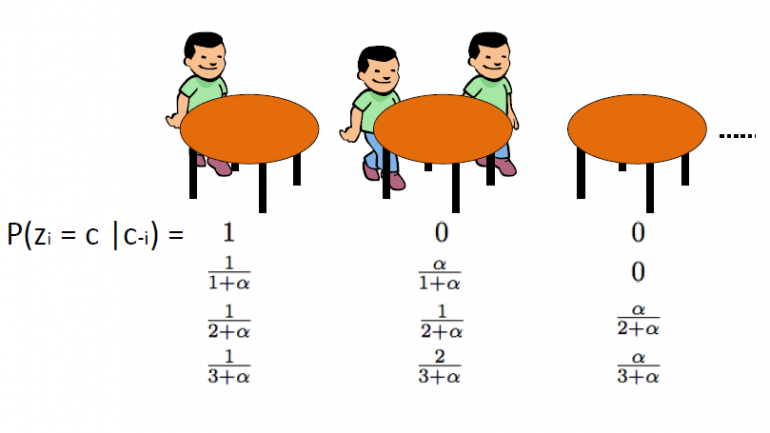Dirichlet Süreci Çin Restoranı Süreci ve diğer temsiller

• Mayıs 20, 2014
• Vasilis Vryniotis
• . Yorum yok

Bu makale Dirichlet Proses Karışım Modelleri ile Kümeleme serisinin üçüncü bölümüdür. Son kez Dirichlet Dağılımına dayalı Sonlu Karışım Modelini tanımlamıştık ve bu modeli nasıl sonsuz hale getirebileceğimize dair sorular sorduk. K kümeleri sonsuzluğa eğilimliyken modelin sınırını alma fikrini kısaca tartıştık, ancak böyle bir nesnenin varlığının önemsiz olmadığını vurguladığımız gibi (başka bir deyişle, aslında bir modelin sınırını nasıl alırız?) “?). Hatırlatmak gerekirse, k'yi sonsuz yapmak istememizin nedeni, bu şekilde verilerdeki toplam küme sayısını önceden tanımlamamızı gerektirmeyen parametrik olmayan bir modele sahip olmamızdır.

Güncelleme: Datumbox Machine Learning Framework artık açık kaynak kodlu ve ücretsiz indir. Java'da Dirichlet Proses Karışım Modellerinin uygulanmasını görmek için com.datumbox.framework.machinelearning.clustering paketini inceleyin.

Hedefimiz veri kümelerinde kümeleme yapabilen bir model oluşturmak olsa da, bundan önce Dirichlet Süreçleri hakkında tartışmalıyız. DP'nin hem katı matematiksel tanımlarını hem de daha sezgisel açıklamalarını sunacağız ve süreci inşa etmenin yollarını tartışacağız. Bu yapılar / temsiller, Dirichlet Sürecinin “gerçek yaşamda” oluşumlarını bulmanın bir yolu olarak görülebilir.

Araştırma raporumu bu blog yazılarının izlenmesi daha kolay olacak şekilde uyarlamaya çalışmamıza rağmen, modelleri kullanmaya başlamadan önce gerekli matematiksel araçları ve dağılımları tanımlamak hala önemlidir. Dirichlet Süreç modelleri aktif bir araştırmanın konusudur, ancak kullanmadan önce İstatistikler ve Stokastik Süreçler hakkında iyi bir anlayışa sahip olmayı gerektirir. Başka bir sorun, bu makalede göreceğimiz gibi, Dirichlet Süreçlerinin çeşitli yollarla temsil edilebileceği / inşa edilebileceğidir. Sonuç olarak birkaç akademik makale tamamen farklı gösterim / konvansiyonlar kullanır ve sorunu farklı açılardan inceler. Bu yazıda onları mümkün olduğunca basit bir şekilde açıklamaya ve aynı gösterimi kullanmaya çalışıyorum. Umarım Dirichlet Proses Karışım Modellerinin tanımına ve bunların küme analizi yapmak için gerçekte nasıl kullanılacağına odaklanan iki makalede işler daha net hale gelecektir.

1. Dirichlet Sürecinin Tanımı

Bir uzayda Dirichlet süreci stokastik bir süreçtir. “Uzay üzerinde olasılık dağılımları” ve ondan ayrılmak ayrık bir dağılımdır. Daha resmi olarak bir Dirichlet Dağılımı olasılık ölçütlerine göre bir dağılımdır. bir olasılık ölçüsü Θ ila [0,1] arasındaki alan alt kümelerinin bir fonksiyonudur. G, DP ile dağıtılan rastgele olasılık ölçüsüdür. , eğer herhangi bir bölüm için (A₁... A_n) alan that bizde var .

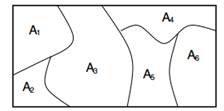
Şekil 1: Sonlu bölümlerdeki marjinaller Dirichlet dağılıdır.

DP'nin iki parametresi vardır: Birincisi taban dağılımı G₀ ortalama gibi hizmet eder . İkincisi, kesinlikle pozitif olan ve ters varyans gibi işlev gören α güç parametresidir. . Çıkış dağılımının değerlerinin tekrarının derecesini belirler. A değeri ne kadar yüksek olursa tekrar o kadar küçük olur; değer ne kadar küçük olursa, çıkış dağılımı değerlerinin tekrarı o kadar yüksek olur. Son olarak Θ alanı, DP'yi tanımladığımız parametre alanıdır. Dahası uzay Θ aynı zamanda G'nin tanım alanıdır.₀ G ile aynı.

Daha basit ve daha fazlası sezgisel yol Dirichlet Sürecini açıklamak için aşağıdaki gibidir. Varsayalım ki herhangi bir sonlu şekilde bölünebilen bir alanımız ((A₁, ..., A_n) ve kendilerine olasılık atayan bir olasılık dağılımı G'dir. G, over üzerinde spesifik bir olasılık dağılımıdır, ancak diğerleri vardır. Dirichlet Süreci Θ modellerinde tam olarak bu; uzay space üzerindeki tüm olası olasılık dağılımları üzerine bir dağılımdır. Dirichlet işlemi G ile parametrelendirilir₀ temel fonksiyon ve α konsantrasyon parametresi. G'nin α ve G parametreleriyle DP'ye göre dağıtıldığını söyleyebiliriz₀ G'nin Θ bölümlerine atadığı olasılıkların ortak dağılımı Dirichlet Dağılımına uyuyorsa. Alternatif olarak, G'nin fin herhangi bir sonlu bölümüne atama olasılıklarının Dirichlet Dağılımını izlediğini söyleyebiliriz.

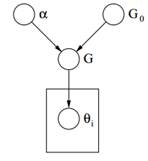
Şekil 2: Dirichlet Sürecinin Grafik Modeli

Sonunda yukarıda DP'nin grafik modeli. Α'nın skaler hiperparametre, G olduğunu not etmeliyiz₀ DP'nin temel dağılımı, G parametrelere olasılıklar atanmış DP'den örneklenen Θ parametre alanı üzerinden rastgele dağılım ve θ_i G dağılımından alınan bir parametre vektörüdür ve Θ uzayının bir elementidir.

2. Posterior Dirichlet Süreçleri

Posterior Dirichlet Süreçleri Ferguson. Dirichlet Sürecinden rastgele olasılık G ölçüsü çizerek başlıyoruz, . G, distribution üzerinde bir olasılık dağılımı olduğu için, bu dağılımdan da numune alabilir ve bağımsız olarak aynı şekilde dağıtılmış örnekler çizebiliriz θ₁,…, Θ_n Bir G. Bir Dirichlet Sürecinden alınan çekimler ayrık dağılımlar olduğundan, nerede için kısa bir gösterimdir hangi delta işlevi 1 alırsa ve 0 başka yerde. Bunun ilginç bir etkisi, G bu şekilde tanımlandığından, aynı değere sahip farklı örneklerin pozitif bir olasılığı vardır. . Daha sonra göreceğimiz gibi, bu, veri kümelerinde Küme Analizi gerçekleştirmek için kullanılabilecek bir kümeleme efekti oluşturur.

Yukarıdaki tanımları ve gözlemleri kullanarak, ich örnekleri verilen Dirichlet Sürecinin posteriorunu tahmin etmek istiyoruz. Yine de bildiğimizden beri ve Bayes Kurallarını ve Dirichlet ile Multinomial arasındaki Konjugatı kullanarak ve .

Denklem 1: Posterior Dirichlet Süreci

Bu özellik çok önemlidir ve çeşitli DP gösterimleri tarafından kullanılır.

3. Dirichlet Süreci gösterimleri

Önceki bölümlerde Dirichlet Sürecini tanımladık ve teorik modelini sunduk. Cevaplamamız gereken önemli bir soru, böyle bir nesnenin var olduğunu nasıl bildiğimiz ve nasıl yapabileceğimizdir inşa et ve temsil et Dirichlet Süreci.

Varlığın ilk belirtileri Ferguson Kolmogorov Tutarlılık Teoremini kullanan, Dirichlet Süreci tanımını vermiş ve Posterior Dirichlet Sürecini tanımlamıştır. Araştırmalarına devam etmek, Blackwell ve MacQueen de Finetti'nin Teoremini böyle rastgele bir olasılık ölçüsünün varlığını kanıtlamak için kullandı ve Dirichlet İşleminin özelliklerini karşılayan Blackwell-MacQueen urn şemasını tanıttı. 1994 yılında sethuraman Stick-break yapıyı tanıtarak bir DP inşa etmenin ek basit ve doğrudan bir yolunu sağladı. Sonunda başka bir temsil Aldous Çin Restoran Süreci'ni Dirichlet Süreci oluşturmak için etkili bir yol olarak tanıtan.

Dirichlet Sürecinin çeşitli Temsili matematiksel olarak eşdeğerdir, ancak formülasyonu farklıdır, çünkü problemi farklı bakış açılarından incelerler. Aşağıda, literatürde bulunan en yaygın gösterimleri sunuyoruz ve Dirichlet Süreci için çıkarım algoritmaları oluşturmak için basit ve hesaplamalı olarak verimli bir yol sağlayan Çin Restoranı Sürecine odaklanıyoruz.

3.1 Blackwell-MacQueen urn şeması

Blackwell-MacQueen urn şeması bir Dirichlet Süreci'ni temsil etmek için kullanılabilir ve Blackwell ve MacQueen. Değiştirilmeden karşı örnekleme modeli olarak görülebilen Pólya urn şemasına dayanmaktadır. Pólya urn şemasında, renkli toplar içeren şeffaf olmayan bir urnumuz olduğunu ve topları rastgele çizdiğimizi varsayıyoruz. Bir top çizdiğimizde, rengini gözlemleriz, tekrar urn'a koyarız ve aynı renkten ek bir top ekleriz. Benzer bir şema Blackwell ve MacQueen tarafından bir Dirichlet Süreci oluşturmak için kullanılır.

Bu şema bir dizi produces üretir₁, θ₂,… ile koşullu olasılıklar . Bu şemada G'nin₀ renkler ve her biri için bir dağıtımdır θ_n semaya yerleştirilen topun rengini temsil eder. algoritma aşağıdaki gibidir:

· Boş bir urn ile başlıyoruz.

· Olasılıkla orantılı olarak α çiziyoruz ve bu rengin bir topunu urn'a ekliyoruz.

· N-1 ile orantılı olarak, urndan rastgele bir top çizeriz, rengini gözlemleriz, tekrar urn'a yerleştiririz ve urn'a aynı renkte ek bir top ekleriz.

Daha önce bir Dirichlet Süreci ile başladık ve Blackwell-MacQueen şemasını türettik. Şimdi tersine Blackwell-MacQueen şemasından başlayalım ve DP'yi türetelim. Θ'den beri_i G'den iid bir şekilde çekildiklerinde, bunların ortak dağılımı herhangi bir sonlu permütasyona değişmeyecek ve bu nedenle değiştirilebilirler. Sonuç olarak, de Finetti'nin teoremini kullanarak, bunları yapmak için önlemler üzerinde bir dağılım olması gerektiğine ve bu dağılımın Dirichlet Süreci olduğunu düşünüyoruz. Sonuç olarak, Blackwell-MacQueen urn şemasının DP'nin bir temsili olduğunu kanıtlıyoruz ve bize bunu inşa etmek için somut bir yol veriyor. Daha sonra göreceğimiz gibi, bu plan matematiksel olarak Çin Restoranı Sürecine eşdeğerdir.

3.2 Yapışmaz yapı

Çubuk kırma yapısı, Dirichlet İşlemini temsil etmenin alternatif bir yoludur. sethuraman. Bu yapıyı oluşturmanın yapıcı bir yoludur. dağıtım ve kullanır benzetmeyi takip etmek: Bir uzunluk çubuğumuza sahip olduğumuzu varsayarız 1, pozisyonda kırıyoruz β₁ ve biz π₁ kırdığımız çubuğun uzunluğuna eşit. Aynı işlemi tekrarlamak için tekrarlıyoruz π₂, Pi₃,… vb; bu şemanın tanımlanma şekli nedeniyle sonsuz kez yapmaya devam edebiliriz.

Yukarıdakilere dayanarak π_k olarak modellenebilir , Burada önceki şemalarda olduğu gibi, θ doğrudan Baz dağılımı ile örneklenir . Sonuç olarak G dağılımı π ile ağırlıklandırılmış delta fonksiyonlarının toplamı olarak yazılabilir._k eşit olasılıklar . Böylece, Sopa kırma yapısı bize bir Dirichlet Süreci oluşturmak için basit ve sezgisel bir yol sağlar.

3.3 Çin Restoranı Süreci

Tarafından tanıtılan Çin Restoranı Süreci Aldous, bir Dirichlet İşlemini temsil etmenin bir başka etkili yoludur ve doğrudan Blackwell-MacQueen urn şemasına bağlanabilir. Bu şema benzetmeyi takip etmek: Sonsuz sayıda masaya sahip bir Çin restoranı olduğunu varsayıyoruz. Müşteriler restorana girdiklerinde işgal edilen masalardan herhangi birine rastgele otururlar ya da mevcut ilk boş masaya oturmayı seçerler.

CRP, pozitif tamsayıların bölümleri uzayında bir dağılım tanımlar. Çizim yaparak başlıyoruz θ₁... θ_n Blackwell-MacQueen urn şemasından. Önceki bölümlerde tartıştığımız gibi, bir kümeleme etkisi görmeyi umuyoruz ve bu nedenle toplam benzersiz θ değeri sayısı n'den önemli ölçüde daha az olacaktır. Böylece bu, kümeler halinde {1,2,…, n} kümesinin bir bölümünü tanımlar. Sonuç olarak, Blackwell-MacQueen urn şemasından çizim, {1,2,…, n} kümesinin rastgele bir bölünmesine neden olur. Çin Lokantası Süreci buna bağlı bölümler arası dağıtım. Algoritma aşağıdaki gibidir:

· Boş bir restoranla başlıyoruz.

· The 1^st müşteri her zaman oturur 1^st tablo

· N + 1^th müşterinin 2 seçeneği vardır:

o Olasılıkla 1. boş masaya oturun

o Olasılıkla kth dolu masaların herhangi birinde oturun
nerede o masada oturan kişi sayısı

Α, DP'nin dağılım değeri ve n, belirli bir zamanda restorandaki toplam müşteri sayısıdır. Gizli değişken z_i i'nin tablo numarasını saklar^th müşteri ve 1'den k'a kadar değerleri alır_n nerede k_n n müşteri restorandayken işgal edilen toplam masa sayısıdır. Dikkat etmeliyiz ki k_n her zaman n'ye eşit veya daha az olacaktır ve ortalama olarak . Son olarak, masa düzenlemesi olasılığının permütasyonlara değişmez. Böylece z_i aynı büyüklükte müşteriye sahip tabloların aynı olasılığa sahip olduğunu ima eden değiştirilebilir.

Çin Restoranı Süreci, Pólya urn şeması ve Dirichlet Süreci ile güçlü bir şekilde bağlantılıdır. CRP, bölümler arası dağıtım (tablo atamaları) n noktadan oluşur ve gizli değişken z boşluğunda bir öncek olarak kullanılabilir_i hangi küme atamalarını belirler. CRP, Pólya'nın urn şemasına eşdeğerdir ve tek farkı her tabloya / kümeye parametre atamamasıdır. Gitmek CRP'den Pólya'nın urn şemasına çiziyoruz tüm tablolar için k = 1,2… ve sonra her x için_i ki bu tablo z olarak gruplandırılmıştır_i ata . Başka bir deyişle, yeni x_i tablonun θ parametresi. Sonunda atayamayız θ başından beri sonsuz tablolara, yeni bir masaya her oturuşunda yeni bir assign atayabiliriz. Yukarıdakilerin tümü nedeniyle, CRP, veri kümelerinde Küme Analizi gerçekleştirmek için hesaplamalı olarak verimli algoritmalar oluşturmamıza yardımcı olabilir.

Bu yazıda Dirichlet Sürecini ve bunu inşa etmenin birkaç yolunu tartıştık. Yukarıdaki fikirleri bir sonraki makalede kullanacağız. Dirichlet Proses Karışım Modelini tanıtacağız ve Dirichlet Prosesini oluşturmak ve Küme Analizini önceden oluşturmak için Çin Restoranı Temsilciliğini kullanacağız. Birkaç noktayı kaçırdıysanız endişelenmeyin, çünkü sonraki iki makalede işler daha net olmaya başlayacaktır.

Umarım bu yazıyı ilginç bulmuşsundur. Bunu yaptıysanız, bir dakikanızı ayırarak Facebook ve Twitter'da paylaşın. 🙂