Нотація Big O та аналіз алгоритмів із прикладами Python

Вступ

Зазвичай існує кілька способів вирішення проблеми за допомогою комп’ютерної програми. Наприклад, є кілька способів сортування елементів у масиві – ви можете використовувати злиття сорту, сортування міхура, сортування вставки, і так далі. Усі ці алгоритми мають свої плюси та мінуси, і завдання розробника полягає в тому, щоб зважити їх, щоб вибрати найкращий алгоритм для будь-якого випадку використання. Іншими словами, головне питання полягає в тому, який алгоритм використовувати для вирішення конкретної проблеми, коли існує кілька рішень проблеми.

Аналіз алгоритму відноситься до аналізу складності різних алгоритмів і пошуку найбільш ефективного алгоритму для вирішення проблеми. Позначення Big-O це статистичний показник, який використовується для опису складності алгоритму.

У цьому посібнику ми спочатку зробимо короткий огляд аналізу алгоритмів, а потім глибше розглянемо нотацію Big-O. Ми побачимо, як нотацію Big-O можна використовувати для визначення складності алгоритму за допомогою різних функцій Python.

Чому аналіз алгоритмів важливий?

Щоб зрозуміти, чому аналіз алгоритмів важливий, скористаємося простим прикладом. Припустимо, менеджер дає завдання двом своїм співробітникам розробити алгоритм на Python, який обчислює факторіал числа, введеного користувачем. Алгоритм, розроблений першим співробітником, виглядає так:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Зверніть увагу, що алгоритм просто приймає ціле число як аргумент. Всередині fact() функція змінна з іменем product ініціалізується до 1. Цикл виконується з 1 до n і під час кожної ітерації значення в product множиться на число, яке повторюється циклом, і результат зберігається в product знову змінна. Після виконання циклу product змінна міститиме факториал.

Так само другий співробітник також розробив алгоритм, який обчислює факторіал числа. Другий співробітник використав рекурсивну функцію, щоб обчислити факторіал числа n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Менеджер повинен вирішити, який алгоритм використовувати. Для цього вони вирішили вибрати, який алгоритм працюватиме швидше. Один із способів зробити це - знайти час, необхідний для виконання коду на тому самому вході.

У блокноті Jupyter ви можете використовувати %timeit літерал, за яким іде виклик функції, щоб знайти час, потрібний функції для виконання:

%timeit fact(50)

Це дасть нам:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

На виході сказано, що алгоритм приймає 9 мікросекунди (плюс/мінус 45 наносекунд) на цикл.

Подібним чином ми можемо обчислити, скільки часу потрібно для виконання другого підходу:

%timeit fact2(50)

Це призведе до:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Другий алгоритм включає рекурсію 15 мікросекунди (плюс/мінус 427 наносекунд).

Час виконання показує, що перший алгоритм є швидшим порівняно з другим алгоритмом, що включає рекурсію. При роботі з великими входами різниця в продуктивності може стати більш значною.

Однак час виконання не є хорошим показником для вимірювання складності алгоритму, оскільки він залежить від апаратного забезпечення. Для алгоритму потрібна більш об’єктивна метрика аналізу складності. Ось де Велика нотація O приходить грати.

Алгоритм аналізу з великою нотацією

Нотація Big-O означає зв’язок між вхідними даними алгоритму та кроками, необхідними для виконання алгоритму. Він позначається великою буквою «О», за якою йдуть відкриваюча та закриваюча дужки. У круглих дужках зв’язок між вхідними даними та кроками, виконаними алгоритмом, представлений за допомогою «n».

Ключовий висновок: Big-O не зацікавлений у a приватність екземпляр, у якому ви запускаєте алгоритм, наприклад fact(50), а скоріше, наскільки добре це робить масштаб враховуючи збільшення вхідних даних. Це набагато кращий показник для оцінки, ніж конкретний час для конкретного екземпляра!

Наприклад, якщо є a лінійна залежність між введенням і кроком, зробленим алгоритмом для завершення його виконання, використана нотація Big-O буде О (п). Аналогічно, позначення Big-O для квадратичні функції is O (n²).

Щоб розвинути інтуїцію:

• О (п): у n=1, зроблено 1 крок. на n=10, зроблено 10 кроків.
• O (n²): у n=1, зроблено 1 крок. на n=10, зроблено 100 кроків.

At n=1, ці двоє діятимуть однаково! Це ще одна причина, чому спостерігати за зв’язком між вхідними даними та кількістю кроків для обробки цих вхідних даних краще, ніж просто оцінювати функції за допомогою певних вхідних даних.

Нижче наведено деякі з найпоширеніших функцій Big-O:

ІМ'Я	Великий О
Постійне	O (c)
Лінійний	О (п)
Квадратний	O (n²)
Кубічний	O(n³)
Exponential	O(2ⁿ)
Логарифмічна	O (журнал (n))
Лінійний журнал	O(nlog(n))

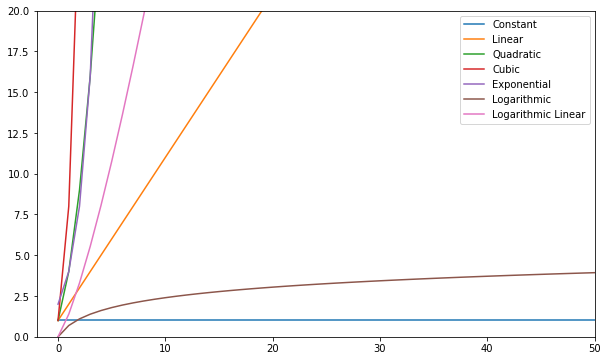
Ви можете візуалізувати ці функції та порівняти їх:

Загалом кажучи, все, що є гірше лінійного, вважається поганою складністю (тобто неефективним) і його слід уникати, якщо можливо. Лінійна складність — це нормально і зазвичай необхідне зло. Логарифміка - це добре. Константа дивовижна!

Щоб отримати уявлення про те, як обчислюється Big-O, давайте розглянемо кілька прикладів постійної, лінійної та квадратичної складності.

Постійна складність – O(C)

Складність алгоритму називається постійною, якщо кроки, необхідні для завершення виконання алгоритму, залишаються постійними, незалежно від кількості вхідних даних. Постійна складність позначається O (c) де c може бути будь-яким постійним числом.

Давайте напишемо простий алгоритм на Python, який знаходить квадрат першого елемента в списку, а потім друкує його на екрані:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

У сценарії вище незалежно від розміру введенняабо кількість елементів у списку введення items, алгоритм виконує лише 2 кроки:

1. Знаходження квадрата першого елемента
2. Виведення результату на екран.

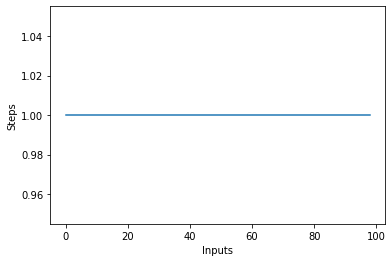
Отже, складність залишається незмінною.

Якщо ви малюєте лінійну ділянку зі змінним розміром items введіть по осі X і кількість кроків по осі Y, ви отримаєте пряму лінію. Давайте створимо короткий сценарій, який допоможе нам уявити це. Незалежно від кількості введених даних, кількість виконаних кроків залишається незмінною:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Лінійна складність – О (п)

Складність алгоритму називається лінійною, якщо кроки, необхідні для завершення виконання алгоритму, зростають або зменшуються лінійно з кількістю вхідних даних. Лінійна складність позначається О (п).

У цьому прикладі давайте напишемо просту програму, яка відображає всі елементи зі списку на консолі:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

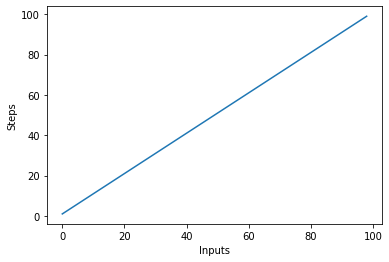
Складність в linear_algo() функція є лінійною у наведеному вище прикладі, оскільки кількість ітерацій циклу for буде дорівнює розміру входу items масив. Наприклад, якщо в items список, цикл for буде виконано 4 рази.

Давайте швидко створимо графік для алгоритму лінійної складності з кількістю вхідних даних на осі х і кількістю кроків на осі у:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Це призведе до:

Важливо зауважити, що при великих вхідних даних константи мають тенденцію втрачати значення. Ось чому ми зазвичай видаляємо константи з нотації Big-O, а такий вираз, як O(2n), зазвичай скорочується до O(n). І O(2n), і O(n) є лінійними – важлива лінійна залежність, а не конкретне значення. Наприклад, давайте змінимо linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

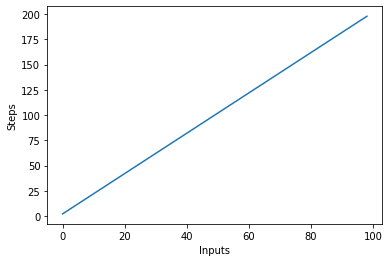
Є два цикли for, які перебирають вхідні дані items список. Тому складність алгоритму стає O (2n), однак у випадку нескінченної кількості елементів у вхідному списку подвійна нескінченність все ще дорівнює нескінченності. Ми можемо знехтувати константою 2 (оскільки це в кінцевому підсумку незначне) і складність алгоритму залишається О (п).

Давайте візуалізуємо цей новий алгоритм, відкладаючи вхідні дані на вісь X і кількість кроків на вісь Y:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

У сценарії вище ви можете це чітко побачити y=2n, однак вихід є лінійним і виглядає так:

Квадратична складність – O (n²)

Складність алгоритму називається квадратичною, якщо кроки, необхідні для виконання алгоритму, є квадратичною функцією кількості елементів у вхідних даних. Квадратична складність позначається як O (n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

У нас є зовнішній цикл, який перебирає всі елементи у вхідному списку, а потім вкладений внутрішній цикл, який знову перебирає всі елементи у вхідному списку. Загальна кількість виконаних кроків дорівнює n*n, де n — кількість елементів у вхідному масиві.

На наступному графіку показано кількість вхідних даних і кроків для алгоритму з квадратичною складністю:

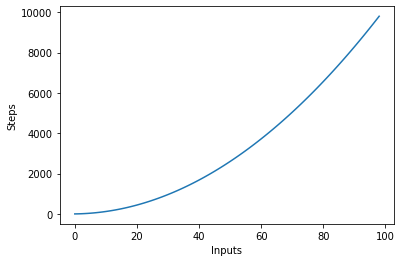
Логарифмічна складність – O (вхід)

Деякі алгоритми досягають логарифмічної складності, наприклад Двійковий пошук. Двійковий пошук шукає елемент у масиві, перевіряючи середній масиву та вирізання половини, у якій елемента немає. Це робиться знову для половини, що залишилася, і продовжує ті самі кроки, доки елемент не буде знайдено. На кожному кроці це половинки кількість елементів у масиві.

Це вимагає, щоб масив був відсортований, а ми зробили припущення щодо даних (наприклад, що вони відсортовані).

Якщо ви можете зробити припущення щодо вхідних даних, ви можете вжити заходів, які зменшать складність алгоритму. Логарифмічна складність є бажаною, оскільки вона забезпечує хорошу продуктивність навіть із високомасштабованим введенням.

Знайти складність складних функцій?

У попередніх прикладах ми мали досить прості функції на вході. Але як ми обчислюємо Big-O для функцій, які викликають (кілька) інші функції на вхідних даних?

Давайте подивимось:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

У наведеному вище сценарії виконується кілька завдань, спочатку рядок друкується 5 разів на консолі за допомогою print заява. Далі ми двічі друкуємо список введення на екрані, і, нарешті, інший рядок друкуємо тричі на консолі. Щоб знайти складність такого алгоритму, нам потрібно розбити код алгоритму на частини та спробувати знайти складність окремих частин. Позначте складність кожної частини.

У першому розділі ми маємо:

for i in range(5):
	print("Python is awesome")

Складність цієї частини полягає в тому O (5) оскільки в цьому фрагменті коду виконується п’ять постійних кроків незалежно від вхідних даних.

Далі маємо:

for item in items:
	print(item)

Ми знаємо, наскільки складним є наведений вище фрагмент коду О (п). Подібним чином, складність наступного фрагмента коду також є О (п):

for item in items:
	print(item)

Нарешті, у наступному фрагменті коду рядок друкується тричі, отже складність O (3):

print("Big O")
print("Big O")
print("Big O")

Щоб знайти загальну складність, нам просто потрібно додати ці окремі складності:

O(5) + O(n) + O(n) + O(3)

Спрощуючи вищесказане, ми отримуємо:

O(8) + O(2n) = O(8+2n)

Раніше ми говорили, що коли вхід (який у цьому випадку має довжину n) стає надзвичайно великим, константи стають незначними, тобто двічі або половина нескінченності все ще залишається нескінченністю. Тому ми можемо знехтувати константами. Остаточна складність алгоритму складе О (п)!

Найгірший і найкращий варіант складності

Зазвичай, коли хтось запитує вас про складність алгоритму, їх цікавить складність у найгіршому випадку (Big-O). Іноді їх також може цікавити найкраща складність (Big-Omega).

Щоб зрозуміти взаємозв’язок між ними, давайте подивимося на іншу частину коду:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

У сценарії вище ми маємо функцію, яка приймає число та список чисел як вхідні дані. Він повертає істину, якщо передане число знайдено у списку чисел, інакше повертає None. Якщо ви шукаєте 2 у списку, він буде знайдений у першому порівнянні. Це найкращий випадок складності алгоритму, оскільки шуканий елемент знаходиться в першому шуканому індексі. Найкращий випадок складності, в даному випадку є O (1). З іншого боку, якщо ви шукаєте 10, його буде знайдено за останнім пошуковим індексом. Алгоритм повинен шукати всі елементи в списку, отже складність у найгіршому випадку стає О (п).

Окрім найкращої та найгіршої складності, ви також можете обчислити середньої складності (Big-Theta) алгоритму, який говорить вам: «Яка очікувана часова складність алгоритму з урахуванням випадкових вхідних даних»?

Складність простору

Окрім часової складності, де ви підраховуєте кількість кроків, необхідних для завершення виконання алгоритму, ви також можете знайти складність простору який стосується обсягу простору, який потрібно виділити в пам’яті під час виконання програми.

Подивіться на наступний приклад:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

Команда return_squares() функція приймає список цілих чисел і повертає список із відповідними квадратами. Алгоритм має виділити пам’ять для такої ж кількості елементів, як у вхідному списку. Тому стає просторовою складністю алгоритму О (п).

Висновок

Нотація Big-O — це стандартна метрика, яка використовується для вимірювання складності алгоритму. У цьому посібнику ми вивчали, що таке нотація Big-O і як її можна використовувати для вимірювання складності різноманітних алгоритмів. Ми також вивчали різні типи функцій Big-O за допомогою різних прикладів Python. Нарешті, ми коротко розглянули найгіршу та найкращу складність, а також просторову складність.