Математики кидають кубики і дістають камінь-ножиці-папір

Як розповідає Білл Гейтс, Уоррен Баффет одного разу викликав його на гру в кості. Кожен вибирав один із чотирьох кубиків, які належали Баффету, а потім кидав, причому вигравав більший номер. Це не були стандартні кубики — вони мали інший асортимент чисел, ніж звичайні кубики від 1 до 6. Баффет запропонував дозволити Гейтсу вибрати першим, щоб він міг вибрати найсильніший кубик. Але після того, як Гейтс перевірив кубики, він повернув зустрічну пропозицію: Баффет повинен вибрати першим.

Ґейтс визнав, що кубики Баффета виявляють цікаву властивість: жодна з них не була найсильнішою. Якби Ґейтс вибрав першим, то який би кубик він не вибрав, Баффетт зміг би знайти інший кубик, який міг би перемогти його (тобто такий, у якого ймовірність перемоги перевищує 50%).

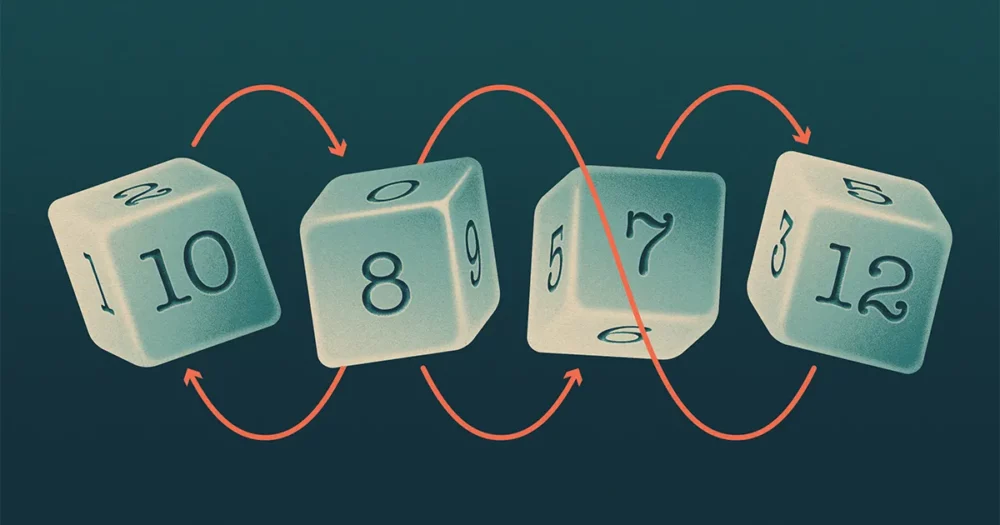
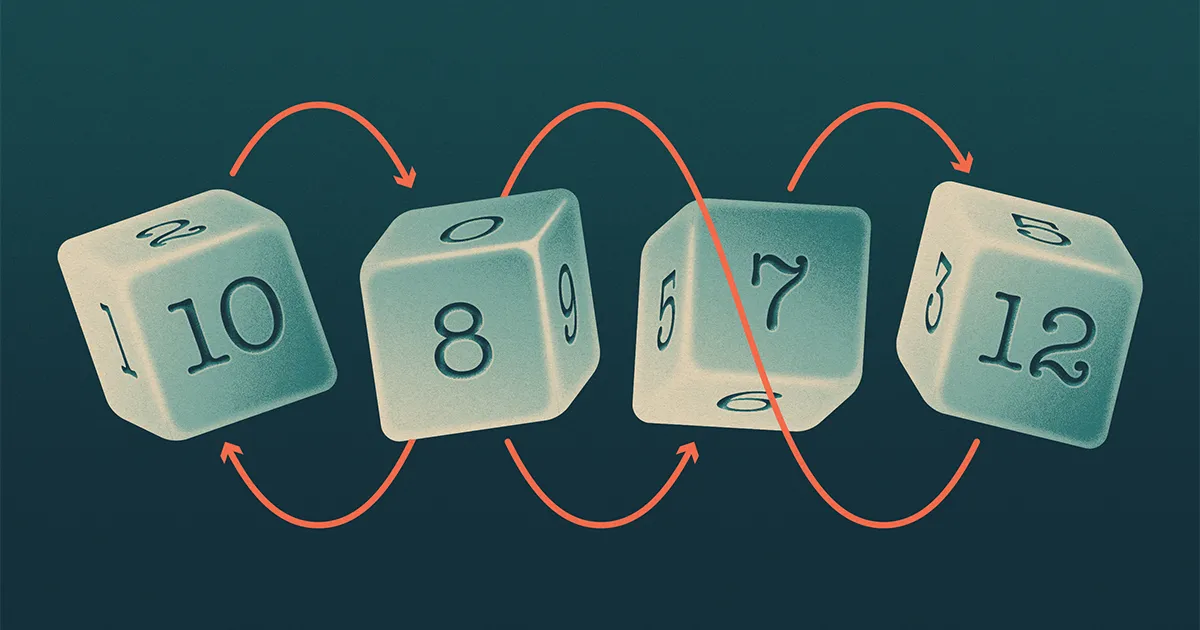
Чотири кубики Баффета (назвіть їх A, B, C та D) утворився візерунок, що нагадує камінь-ножиці-папір, в якому A ударів B, B ударів C, C ударів D та D ударів A. Математики кажуть, що такий набір кубиків «неперехідний».

«Зовсім не інтуїтивно зрозуміло, що [неперехідні кубики] взагалі повинні існувати», — сказав Браян Конрі, директор Американського інституту математики (AIM) у Сан-Хосе, який написав впливову статтю на цю тему в 2013 році.

Математики придумали перші приклади неперехідних кубиків понад 50 років тому, і врешті-решт доведений що коли ви розглядаєте кубики з дедалі більшою кількістю сторін, можна створювати неперехідні цикли будь-якої довжини. Математики донедавна не знали, наскільки поширені неперехідні кубики. Чи потрібно ретельно вигадувати такі приклади, чи можна вибирати кубики випадковим чином і мати хороші шанси знайти неперехідний набір?

Дивлячись на три кубики, якщо ви це знаєте A ударів B та B ударів C, це здається доказом того A є найсильнішим; ситуації, коли C ударів A має бути рідкісним. І справді, якщо числам на кубиках дозволено складати різні суми, то математики вважають, що ця інтуїція вірна.

Але а документ, розміщений в Інтернеті кінець минулого року показує, що в іншій природній обстановці ця інтуїція вражаюче провалюється. Припустімо, ви вимагаєте, щоб ваші гральні кістки використовували лише числа, які зображені на звичайному кубику, і мали таку ж суму, як і на звичайному кубику. Потім на папері було показано, якщо A ударів B та B ударів C, A та C мають по суті рівні шанси перемогти один над одним.

«Знаючи це A ударів B та B ударів C просто не дає вам інформації про те, чи A ударів C, - сказав він Тімоті Гауерс Кембриджського університету, медаліст Філдса та один із учасників нового результату, який було доведено через відкриту онлайн-співпрацю, відому як проект Polymath.

Тим часом інший недавній документ аналізує набори з чотирьох або більше кубиків. Цей висновок, мабуть, ще більш парадоксальний: якщо, наприклад, ви навмання виберете чотири кубики і виявите, що A ударів B, B ударів C та C ударів D, то це трохи більше ймовірно для D бити A ніж навпаки.

Ні Сильний, ні Слабкий

Недавній сплеск результатів почався приблизно десять років тому, після того, як Конрі відвідав зустріч для вчителів математики з сеансом, який охоплював неперехідні кубики. «Я поняття не мав, що такі речі можуть існувати», — сказав він. «Я був ними зачарований».

Він вирішив (згодом до нього приєднався його колега Кент Моррісон в AIM), щоб дослідити цю тему з трьома учнями середньої школи, яких він наставляв — Джеймсом Ґаббардом, Кеті Грант та Ендрю Лю. Як часто, запитувала група, навмання вибрані кубики утворюють неперехідний цикл?

Вважається, що неперехідні набори гральних кубиків є рідкісними, якщо сумарні номери гральних кубиків дають різні суми, оскільки кубик із найбільшою сумою, швидше за все, перевершить інші. Тож команда вирішила зосередитися на кубиках, які мають дві властивості: по-перше, у кубиках використовуються ті самі числа, що й на стандартному кубику — від 1 до n, у випадку ан n- одностороння плашка. По-друге, сумарні номери граней дають таку саму загальну суму, як і на стандартному кубику. Але на відміну від стандартних кубиків, кожен кубик може повторювати деякі числа та пропускати інші.

У випадку з шестигранними кубиками існує лише 32 різні кубики, які мають ці дві властивості. Тож за допомогою комп’ютера команда могла ідентифікувати всі трійки, у яких A ударів B та B ударів C. Дослідники виявили, на свій подив, що A ударів C в 1,756 потрійних і C ударів A у 1,731 трійці — майже однакові числа. На основі цього обчислення та симуляції гральних кубиків із більш ніж шістьма сторонами, припустила команда що, коли кількість сторін грального кубика наближається до нескінченності, ймовірність того, що A ударів C наближається до 50%.

Гіпотеза, з її поєднанням доступності та нюансів, вразила Конрі як хороший корм для проекту Polymath, у якому багато математиків збираються онлайн, щоб поділитися ідеями. У середині 2017 року він запропонував цю ідею Гауерсу, автору підходу Polymath. «Мені дуже сподобалося запитання через його несподіванку», — сказав Гауерс. Він написав а блог про припущення, яке викликало шквал коментарів, і протягом шести додаткових постів коментаторам вдалося це довести.

У своїй роботі розміщено в Інтернеті наприкінці листопада 2022 року ключова частина доказу полягає в тому, щоб показати, що здебільшого немає сенсу говорити про те, чи один кубик є сильним чи слабким. Гральні кубики Баффета, жоден із яких не є найсильнішим у наборі, не такі вже й незвичайні: якщо ви виберете кубик навмання, проект Polymath показав, що він, швидше за все, перевершить приблизно половину інших кубиків і програє іншій половині. «Майже кожен кубик досить середній», — сказав Гауерс.

Проект відрізнявся від оригінальної моделі команди AIM в одному аспекті: щоб спростити деякі технічні моменти, проект заявив, що порядок чисел на кубику має значення — тому, наприклад, 122556 і 152562 вважатимуться двома різними гральними кубиками. Але результати Polymath у поєднанні з експериментальними доказами команди AIM створюють сильне припущення, що гіпотеза також вірна в оригінальній моделі, сказав Гауерс.

«Я був дуже радий, що вони знайшли цей доказ», — сказав Конрі.

Коли справа дійшла до колекції з чотирьох або більше кубиків, команда AIM передбачила поведінку, подібну до поведінки трьох кубиків: наприклад, якщо A ударів B, B ударів C та C ударів D тоді ймовірність того повинна бути приблизно 50-50 D ударів A, наближаючись рівно до 50-50, оскільки кількість сторін кубика наближається до нескінченності.

Щоб перевірити припущення, дослідники змоделювали особисті турніри для наборів із чотирьох кубиків із 50, 100, 150 та 200 сторонами. Симуляції не відповідали їхнім прогнозам настільки точно, як у випадку з трьома гральними кубиками, але все ж були достатньо близькими, щоб зміцнити їхню віру в припущення. Але хоча дослідники цього не усвідомлювали, ці невеликі розбіжності несли інше повідомлення: для наборів із чотирьох або більше кубиків їх припущення є хибним.

«Ми дуже хотіли, щоб [гіпотеза] була правдою, тому що це було б круто», — сказав Конрі.

У випадку з чотирма кубиками, Елізабетта Корнаккіа Швейцарського федерального технологічного інституту Лозанни та Ян Хозла Африканського інституту математичних наук у Кігалі, Руанда, показано в a папір опубліковано в Інтернеті наприкінці 2020 року, що якщо A ударів B, B ударів C та C ударів D, То D має трохи більше ніж 50% шансів перемогти A — ймовірно, десь близько 52%, сказав Газла. (Як і у статті Polymath, Cornacchia та Hązła використовували дещо іншу модель, ніж у статті AIM.)

Висновок Корнаккіа та Газли випливає з того факту, що хоча, як правило, один кубик не буде ані сильним, ані слабким, пара кубиків іноді може мати загальну силу. Якщо вибрати два кубики навмання, Cornacchia та Hązła показали, існує пристойна ймовірність того, що кубики будуть співвідносними: вони, як правило, будуть перемагати або програвати тим самим кубикам. «Якщо я попрошу вас створити дві кістки, розташовані близько одна до одної, виявиться, що це можливо», — сказав Хозла. Ці невеликі кишені кореляції відштовхують результати турніру від симетрії, щойно на зображенні є принаймні чотири кубики.

Останні статті — це ще не кінець історії. Стаття Корнаккіа та Газли лише починає розкривати, як саме кореляції між кубиками дисбалансують симетрію турнірів. Тим часом ми знаємо, що існує безліч наборів неперехідних кубиків — можливо, навіть такий, який досить тонкий, щоб змусити Білла Гейтса вибрати першим.