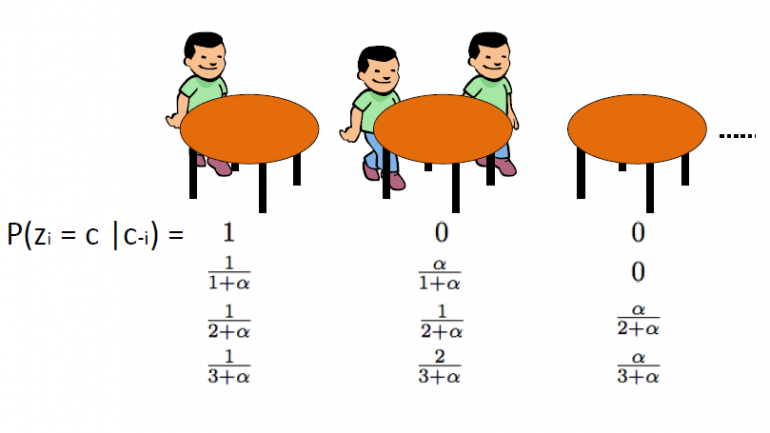Процес Діріхле - процес китайського ресторану та інші уявлення

• Травень 20, 2014
• Василіс Врініотис
• . Без коментарів

Ця стаття є третьою частиною серії про кластеризацію за допомогою моделей суміші процесу Діріхле. Попереднього разу ми визначили модель кінцевої суміші на основі розподілу Діріхле та поставили запитання про те, як ми можемо зробити цю модель нескінченною. Ми коротко обговорили ідею взяти межу моделі, коли кількість k кластерів прагне до нескінченності, але, як ми підкреслили, існування такого об’єкта не є тривіальним (іншими словами, як ми насправді «беремо межу моделі ”?). Нагадуємо, що причина, чому ми хочемо зробити k нескінченним, полягає в тому, що таким чином ми матимемо непараметричну модель, яка не вимагає від нас попереднього визначення загальної кількості кластерів у даних.

Оновлення: Система машинного навчання Datumbox тепер є відкритою та безкоштовною скачати. Перевірте пакет com.datumbox.framework.machinelearning.clustering, щоб побачити реалізацію моделей суміші процесів Діріхле на Java.

Незважаючи на те, що нашою метою є створення моделі, здатної виконувати кластеризацію наборів даних, перед цим ми повинні обговорити процеси Діріхле. Ми надамо як строгі математичні визначення, так і більш інтуїтивні пояснення DP, а також обговоримо способи побудови процесу. Ці конструкції/уявлення можна розглядати як спосіб знайти випадки процесу Діріхле в «реальному житті».

Незважаючи на те, що я намагався адаптувати свій дослідницький звіт таким чином, щоб було легше стежити за цими публікаціями в блозі, все одно важливо визначити необхідні математичні інструменти та розподіл перед тим, як ми приступимо до використання моделей. Моделі процесу Діріхле є темою для активних досліджень, але вони вимагають хорошого розуміння статистики та стохастичних процесів перед їх використанням. Інша проблема полягає в тому, що, як ми побачимо в цій статті, процеси Діріхле можна представити/побудувати багатьма способами. Як наслідок, у кількох наукових статтях використовуються абсолютно різні позначення/конвенції та розглядається проблема з різних точок зору. У цій публікації я намагаюся пояснити їх якомога простіше та використовувати ті самі позначення. Сподіваюся, все стане зрозумілішим із двома майбутніми статтями, які зосереджуються на визначенні моделей процесу Діріхле та на тому, як їх фактично використовувати для виконання кластерного аналізу.

1. Визначення процесу Діріхле

Процес Діріхле над простором Θ є випадковим процесом. Це розподіл ймовірностей у «розподілі ймовірностей у просторі Θ» та a отримати з нього дискретний розподіл. Формальніше кажучи, розподіл Діріхле — це розподіл за ймовірнісними мірами. А міра ймовірності є функцією підмножин простору Θ до [0,1]. G — розподілена випадкова ймовірнісна міра DP, позначена як , якщо для будь-якого розділу (A₁,…А_n) простору Θ маємо це .

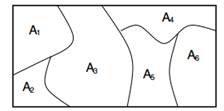
Рисунок 1: Маргінали на скінченних розбиттях є розподіленими Діріхле.

DP має два параметри: перший – базовий розподіл G₀ який служить засобом . Другим є параметр міцності α, який є строго додатним і служить як зворотна дисперсія . Він визначає ступінь повторення значень вихідного розподілу. Чим вище значення a, тим менше повторення; чим менше значення, тим більша повторюваність значень розподілу випуску. Нарешті, простір Θ є простором параметрів, на якому ми визначаємо DP. Крім того, простір Θ також є простором визначення G₀ який такий самий, як і Г.

Простіше і більше інтуїтивно зрозумілий спосіб для пояснення процесу Діріхле є наступне. Припустимо, що ми маємо простір Θ, який можна розбити будь-яким кінцевим способом (A₁,…,А_n) і розподіл ймовірностей G, який призначає їм імовірності. G — це певний розподіл ймовірностей по Θ, але є багато інших. Процес Діріхле на Θ моделює саме це; це розподіл за всіма можливими розподілами ймовірностей у просторі Θ. Процес Діріхле параметризовано за допомогою G₀ базова функція та параметр концентрації α. Можна сказати, що G розподілено відповідно до DP з параметрами α і G₀ якщо спільний розподіл ймовірностей, які G приписує розділам Θ, відповідає розподілу Діріхле. Крім того, ми можемо сказати, що ймовірності, які G приписує будь-якій скінченній частині Θ, відповідають розподілу Діріхле.

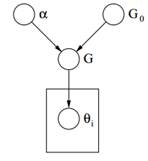
Рисунок 2: Графічна модель процесу Діріхле

Нарешті вище ми можемо побачити графічна модель ДП. Слід зазначити, що α є скалярним гіперпараметром G₀ базовий розподіл DP, G випадковий розподіл у просторі параметрів Θ, відібраний із DP, який призначає ймовірності параметрам, а θ_i це вектор параметрів, який витягується з розподілу G і є елементом простору Θ.

2. Задні відростки Діріхле

Задні процеси Діріхле обговорювали Фергюсон. Ми починаємо з малювання випадкової ймовірнісної міри G із процесу Діріхле, . Оскільки G є розподілом ймовірностей по Θ, ми також можемо робити вибірку з цього розподілу та складати незалежні однаково розподілені вибірки θ₁,…, θ_n ~ G. Оскільки результати процесу Діріхле є дискретними розподілами, ми можемо представити де є коротким позначенням для яка є дельта-функцією, яка приймає 1 якщо і 0 в іншому місці. Цікавим ефектом цього є те, що оскільки G визначено таким чином, існує позитивна ймовірність того, що різні вибірки матимуть однакове значення . Як ми побачимо пізніше, це створює ефект кластеризації, який можна використовувати для виконання кластерного аналізу наборів даних.

Використовуючи наведені вище визначення та спостереження, ми хочемо оцінити задню частину процесу Діріхле з урахуванням зразків θ. Тим не менш, оскільки ми це знаємо та використовуючи правила Байєса та спряженість між Діріхле та багаточленом, ми маємо це та .

Рівняння 1: Задній процес Діріхле

Ця властивість є дуже важливою, і вона використовується різними представленнями DP.

3. Представлення процесу Діріхле

У попередніх сегментах ми визначили процес Діріхле та представили його теоретичну модель. Одне важливе питання, на яке ми повинні відповісти, полягає в тому, як ми дізнаємося, що такий об'єкт існує, і як ми можемо це зробити конструювати та представляти процес Діріхле.

Перші ознаки існування були надані Фергюсон який використав теорему узгодженості Колмогорова, дав визначення процесу Діріхле та описав задній процес Діріхле. Продовжуючи свої дослідження, Блеквелл і Макквін використав теорему де Фінетті, щоб довести існування такої випадкової ймовірнісної міри, і ввів урнову схему Блеквелла-Маккуїна, яка задовольняє властивості процесу Діріхле. У 1994 році Сетураман забезпечив додатковий простий і прямий спосіб побудови DP, ввівши конструкцію Stick-breaking. Нарешті інше представлення було надано Олдос який представив процес китайського ресторану як ефективний спосіб побудови процесу Діріхле.

Різні уявлення про процес Діріхле є математично еквівалентними, але їх формулювання відрізняються, оскільки вони розглядають проблему з різних точок зору. Нижче ми представляємо найпоширеніші представлення, знайдені в літературі, і зосереджуємося на Процесі китайського ресторану, який забезпечує простий і обчислювально ефективний спосіб побудови алгоритмів висновку для Процесу Діріхле.

3.1 Схема урни Блеквелла-МакКвіна

Схему урни Блеквелла-МакКуїна можна використовувати для представлення процесу Діріхле, і вона була представлена Блеквелл і Макквін. Він заснований на урновій схемі Pólya, яку можна розглядати як протилежну модель відбору проб без заміни. У схемі урни Pólya ми припускаємо, що у нас є непрозора урна, яка містить кольорові кулі, і ми витягуємо кулі випадковим чином. Коли ми тягнемо кулю, ми спостерігаємо за її кольором, повертаємо її в урну і додаємо додаткову кулю того ж кольору. Подібну схему використовують Блеквелл і МакКвін для побудови процесу Діріхле.

Ця схема створює послідовність θ₁,θ₂,… з умовні ймовірності . У цій схемі ми припускаємо, що G₀ є розподілом за кольорами та кожним θ_n представляє колір кулі, яка поміщається в урну. The алгоритм полягає в наступному:

· Починаємо з порожньої урни.

· З імовірністю, пропорційною α малюємо і ми додаємо кульку цього кольору в урну.

· З імовірністю, пропорційною n-1, ми витягуємо випадкову кулю з урни, спостерігаємо за її кольором, поміщаємо її назад в урну і додаємо в урну додаткову кулю того ж кольору.

Раніше ми почали з процесу Діріхле та вивели схему Блеквелла-МакКвіна. Тепер давайте почнемо зворотно від схеми Блеквелла-МакКуїна та виведемо DP. Оскільки θ_i були взяті iid способом з G, їхній спільний розподіл буде інваріантним для будь-яких кінцевих перестановок, і, отже, їх можна замінити. Отже, використовуючи теорему де Фінетті, ми маємо, що повинен існувати розподіл за мірами, щоб зробити їх iid, і цей розподіл є процесом Діріхле. У результаті ми доводимо, що схема урни Блеквелла-МакКуїна є представленням DP і дає нам конкретний спосіб її побудови. Як ми побачимо пізніше, ця схема математично еквівалентна процесу китайського ресторану.

3.2 Конструкція, що ламає палку

Конструкція «розбивання паличок» є альтернативним способом представлення процесу Діріхле, який запровадив Сетураман. Це конструктивний спосіб формування розповсюдження та використовує наступна аналогія: Припустимо, що ми маємо паличку довжиною 1, ламаємо її в положенні β₁ і приписуємо π₁ дорівнює довжині частини палиці, яку ми зламали. Ми повторюємо той самий процес, щоб отримати π₂, Пі₃,… тощо; завдяки тому, як ця схема визначена, ми можемо продовжувати робити це нескінченно багато разів.

Виходячи з наведеного вище, π_k можна моделювати як , Де в той час як, як і в попередніх схемах, θ відбираються безпосередньо базовим розподілом . Отже, розподіл G можна записати як суму дельта-функцій, зважених на π_k ймовірності, що дорівнює . Таким чином, конструкція руйнування паличок дає нам простий та інтуїтивно зрозумілий спосіб побудови процесу Діріхле.

3.3 Процес китайського ресторану

Процес китайського ресторану, який запровадив Олдос, є ще одним ефективним способом представлення процесу Діріхле, і його можна безпосередньо пов’язати зі схемою урни Блеквелла-МакКвіна. Ця схема використовує наступна аналогія: Ми припускаємо, що існує китайський ресторан із нескінченною кількістю столиків. Коли клієнти заходять до ресторану, вони випадковим чином сідають за будь-який із зайнятих столиків або вибирають сісти за перший вільний столик.

CRP визначає розподіл на просторі розділів натуральних чисел. Ми починаємо з малювання θ₁,…θ_n зі схеми урни Блеквелла-МакКуїна. Як ми обговорювали в попередніх сегментах, ми очікуємо ефекту кластеризації, і, отже, загальна кількість унікальних значень θ k буде значно меншою за n. Таким чином, це визначає розбиття набору {1,2,…,n} на k кластерів. Отже, малюнок зі схеми урни Блеквелла-МакКуїна індукує випадковий розподіл множини {1,2,…,n}. Процес китайського ресторану викликаний цим розподіл по перегородках. Алгоритм наступний:

· Починаємо з порожнього ресторану.

· 1^st клієнт завжди сидить на 1^st таблиця

· n+1^th клієнт має 2 варіанти:

o З ймовірністю сісти на 1-й незайнятий стіл

o Сісти за будь-який із k-х зайнятих столів з імовірністю
де це кількість людей, які сидять за цим столом

Де α – значення дисперсії DP, а n – загальна кількість клієнтів у ресторані в певний момент часу. Прихована змінна z_i зберігає номер таблиці i^th клієнта і приймає значення від 1 до k_n де k_n – загальна кількість зайнятих столиків, коли в ресторані знаходяться n клієнтів. Слід зазначити, що к_n завжди буде менше або дорівнює n і в середньому становить приблизно . Наостанок зазначимо, що ймовірність розташування столу є інваріантним до перестановок. Таким чином z_i є обмінним, що означає, що таблиці з однаковим розміром клієнтів мають однакову ймовірність.

Процес китайського ресторану тісно пов’язаний зі схемою урни Поліа та процесом Діріхле. CRP – це спосіб визначити a розподіл по перегородках (табличні присвоєння) n точок і може бути використаний як апріор на просторі латентної змінної z_i який визначає призначення кластерів. CRP еквівалентна схемі urn Pólya з тією лише різницею, що вона не призначає параметри кожній таблиці/кластеру. Йти від CRP до схеми урни Поля малюємо для всіх таблиць k=1,2… а потім для кожного x_i який згруповано в таблицю z_i призначити а . Іншими словами, призначити новому x_i параметр θ табл. Нарешті з тих пір ми не можемо призначити θ для нескінченних столів з самого початку, ми можемо просто призначити новий θ кожного разу, коли хтось сідає за новий стіл. Завдяки всьому вищезазначеному, CRP може допомогти нам створити обчислювально ефективні алгоритми для виконання кластерного аналізу наборів даних.

У цій публікації ми обговорили процес Діріхле та кілька способів його побудови. Ми використаємо наведені вище ідеї в наступній статті. Ми представимо модель суміші процесу Діріхле та використаємо представництво китайського ресторану, щоб побудувати процес Діріхле та провести кластерний аналіз. Якщо ви пропустили кілька моментів, не хвилюйтеся, оскільки з наступними двома статтями все стане зрозумілішим.

Сподіваюся, вам ця публікація була цікава. Якщо так, знайдіть хвилинку, щоб поділитися цим у Facebook і Twitter. 🙂