Phân tích ký hiệu và thuật toán Big O với các ví dụ Python

Giới thiệu

Thường có nhiều cách để giải quyết vấn đề bằng chương trình máy tính. Ví dụ: có một số cách để sắp xếp các mục trong một mảng - bạn có thể sử dụng hợp nhất sắp xếp, phân loại bong bóng, sắp xếp chèn, và như thế. Tất cả các thuật toán này đều có ưu và nhược điểm riêng và công việc của nhà phát triển là cân nhắc chúng để có thể chọn ra thuật toán tốt nhất sử dụng trong mọi trường hợp sử dụng. Nói cách khác, câu hỏi chính là sử dụng thuật toán nào để giải quyết một vấn đề cụ thể khi tồn tại nhiều giải pháp cho vấn đề đó.

Phân tích thuật toán đề cập đến việc phân tích độ phức tạp của các thuật toán khác nhau và tìm ra thuật toán hiệu quả nhất để giải quyết vấn đề đang gặp phải. Ký hiệu Big-O là một thước đo thống kê được sử dụng để mô tả độ phức tạp của thuật toán.

Trong hướng dẫn này, trước tiên chúng ta sẽ xem xét ngắn gọn về phân tích thuật toán và sau đó xem xét sâu hơn về ký hiệu Big-O. Chúng ta sẽ xem cách ký hiệu Big-O có thể được sử dụng để tìm độ phức tạp của thuật toán với sự trợ giúp của các hàm Python khác nhau.

Tại sao Phân tích thuật toán lại quan trọng?

Để hiểu tại sao phân tích thuật toán lại quan trọng, chúng tôi sẽ lấy sự trợ giúp của một ví dụ đơn giản. Giả sử một người quản lý giao một nhiệm vụ cho hai nhân viên của mình để thiết kế một thuật toán bằng Python để tính giai thừa của một số do người dùng nhập vào. Thuật toán được phát triển bởi nhân viên đầu tiên trông giống như sau:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Lưu ý rằng thuật toán chỉ đơn giản lấy một số nguyên làm đối số. Bên trong fact() hàm một biến có tên product được khởi tạo thành 1. Một vòng lặp thực thi từ 1 đến n và trong mỗi lần lặp, giá trị trong product được nhân với số được lặp lại bởi vòng lặp và kết quả được lưu trữ trong product biến lại. Sau khi vòng lặp thực thi, product biến sẽ chứa giai thừa.

Tương tự, nhân viên thứ hai cũng phát triển một thuật toán tính giai thừa của một số. Nhân viên thứ hai đã sử dụng một hàm đệ quy để tính giai thừa của số n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Người quản lý phải quyết định sử dụng thuật toán nào. Để làm như vậy, họ đã quyết định chọn thuật toán nào chạy nhanh hơn. Một cách để làm như vậy là tìm thời gian cần thiết để thực thi mã trên cùng một đầu vào.

Trong sổ ghi chép Jupyter, bạn có thể sử dụng %timeit theo sau là lệnh gọi hàm để tìm thời gian hàm thực thi:

%timeit fact(50)

Điều này sẽ cung cấp cho chúng tôi:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Kết quả đầu ra cho biết thuật toán có 9 micro giây (cộng / trừ 45 nano giây) trên mỗi vòng lặp.

Tương tự, chúng ta có thể tính toán thời gian mà cách tiếp cận thứ hai cần để thực thi:

%timeit fact2(50)

Điều này sẽ dẫn đến:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Thuật toán thứ hai liên quan đến đệ quy có 15 micro giây (cộng / trừ 427 nano giây).

Thời gian thực hiện cho thấy thuật toán đầu tiên nhanh hơn so với thuật toán thứ hai liên quan đến đệ quy. Khi xử lý các đầu vào lớn, sự khác biệt về hiệu suất có thể trở nên đáng kể hơn.

Tuy nhiên, thời gian thực thi không phải là thước đo tốt để đo độ phức tạp của một thuật toán vì nó phụ thuộc vào phần cứng. Cần có một số liệu phân tích độ phức tạp khách quan hơn cho một thuật toán. Đây là nơi Ký hiệu O lớn đến chơi

Phân tích thuật toán với ký hiệu Big-O

Ký hiệu Big-O biểu thị mối quan hệ giữa đầu vào cho thuật toán và các bước cần thiết để thực thi thuật toán. Nó được biểu thị bằng chữ “O” lớn theo sau là dấu ngoặc đơn mở và đóng. Bên trong dấu ngoặc đơn, mối quan hệ giữa đầu vào và các bước được thực hiện bởi thuật toán được trình bày bằng cách sử dụng “n”.

Điểm mấu chốt là - Big-O không quan tâm đến riêng ví dụ mà bạn chạy một thuật toán, chẳng hạn như fact(50), nhưng đúng hơn, nó hoạt động tốt như thế nào tỉ lệ đầu vào ngày càng tăng. Đây là một số liệu tốt hơn nhiều để đánh giá so với thời gian cụ thể cho một ví dụ cụ thể!

Ví dụ, nếu có mối quan hệ tuyến tính giữa đầu vào và bước được thực hiện bởi thuật toán để hoàn thành quá trình thực thi của nó, ký hiệu Big-O được sử dụng sẽ là O (n). Tương tự, ký hiệu Big-O cho hàm bậc hai is O (n²).

Để xây dựng trực giác:

• O (n): tại n=1, 1 bước được thực hiện. Tại n=10, 10 bước được thực hiện.
• O (n²): tại n=1, 1 bước được thực hiện. Tại n=10, 100 bước được thực hiện.

At n=1, hai cái này sẽ hoạt động giống nhau! Đây là một lý do khác tại sao việc quan sát mối quan hệ giữa đầu vào và số bước xử lý đầu vào đó tốt hơn là chỉ đánh giá các chức năng với một số đầu vào cụ thể.

Sau đây là một số hàm Big-O phổ biến nhất:

Họ tên	O lớn
Liên tục	O (c)
tuyến tính	O (n)
Phương trình bậc hai	O (n²)
Hình khối	O (n³)
Exponential	O (2ⁿ)
Lôgarit	O (log (n))
Nhật ký tuyến tính	O (nlog (n))

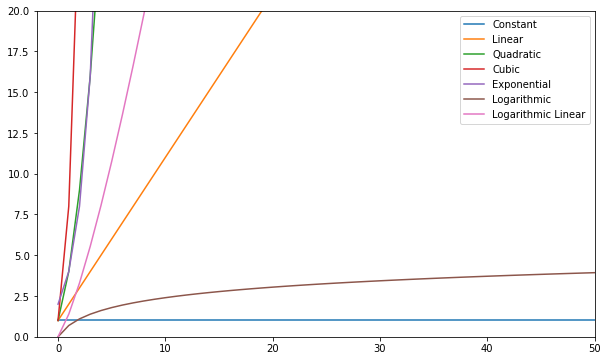
Bạn có thể hình dung các chức năng này và so sánh chúng:

Nói chung - bất kỳ thứ gì tệ hơn tuyến tính đều được coi là phức tạp xấu (tức là không hiệu quả) và nên tránh nếu có thể. Độ phức tạp tuyến tính là ổn và thường là một điều ác cần thiết. Logarit là tốt. Hằng số là tuyệt vời!

Để có ý tưởng về cách tính toán Big-O, chúng ta hãy xem một số ví dụ về độ phức tạp không đổi, tuyến tính và bậc hai.

Độ phức tạp không đổi - O (C)

Độ phức tạp của một thuật toán được cho là không đổi nếu các bước cần thiết để hoàn thành việc thực thi một thuật toán không đổi, bất kể số lượng đầu vào. Độ phức tạp không đổi được biểu thị bằng O (c) Ở đâu c có thể là bất kỳ số không đổi nào.

Hãy viết một thuật toán đơn giản bằng Python để tìm hình vuông của mục đầu tiên trong danh sách và sau đó in nó ra màn hình:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

Trong đoạn mã ở trên, không phân biệt kích thước đầu vàohoặc số lượng mục trong danh sách đầu vào items, thuật toán chỉ thực hiện 2 bước:

1. Tìm bình phương của phần tử đầu tiên
2. In kết quả trên màn hình.

Do đó, độ phức tạp vẫn không đổi.

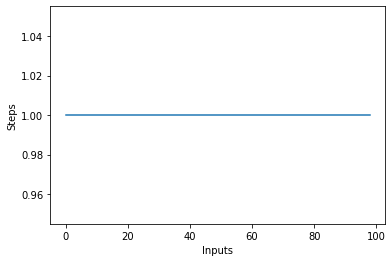
Nếu bạn vẽ một biểu đồ đường với kích thước thay đổi của items đầu vào trên trục X và số bước trên trục Y, bạn sẽ nhận được một đường thẳng. Hãy tạo một kịch bản ngắn để giúp chúng ta hình dung điều này. Bất kể số lượng đầu vào, số lượng các bước được thực hiện vẫn như nhau:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Độ phức tạp tuyến tính - O (n)

Độ phức tạp của một thuật toán được cho là tuyến tính nếu các bước cần thiết để hoàn thành việc thực hiện một thuật toán tăng hoặc giảm tuyến tính với số lượng đầu vào. Độ phức tạp tuyến tính được biểu thị bằng O (n).

Trong ví dụ này, hãy viết một chương trình đơn giản hiển thị tất cả các mục trong danh sách vào bảng điều khiển:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Sự phức tạp của linear_algo() hàm là tuyến tính trong ví dụ trên vì số lần lặp lại của vòng lặp for sẽ là bằng kích thước của đầu vào items mảng. Ví dụ: nếu có 4 mục trong items danh sách, vòng lặp for sẽ được thực hiện 4 lần.

Hãy nhanh chóng tạo một biểu đồ cho thuật toán độ phức tạp tuyến tính với số lượng đầu vào trên trục x và số bước trên trục y:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Điều này sẽ dẫn đến:

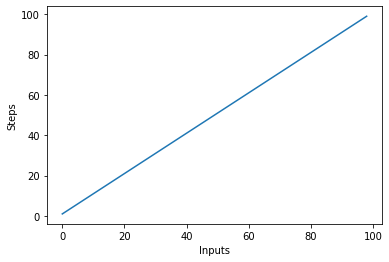
Một điều quan trọng cần lưu ý là với các đầu vào lớn, các hằng số có xu hướng mất giá trị. Đây là lý do tại sao chúng ta thường loại bỏ các hằng số khỏi ký hiệu Big-O và một biểu thức như O (2n) thường được rút gọn thành O (n). Cả O (2n) và O (n) đều tuyến tính - mối quan hệ tuyến tính mới là vấn đề quan trọng, không phải giá trị cụ thể. Ví dụ: hãy sửa đổi linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Có hai vòng lặp for lặp qua đầu vào items danh sách. Do đó, độ phức tạp của thuật toán trở nên O (2n), tuy nhiên trong trường hợp có vô hạn mục trong danh sách đầu vào, hai lần vô cùng vẫn bằng vô cùng. Chúng ta có thể bỏ qua hằng số 2 (vì cuối cùng nó không đáng kể) và độ phức tạp của thuật toán vẫn O (n).

Hãy hình dung thuật toán mới này bằng cách vẽ biểu đồ đầu vào trên trục X và số bước trên trục Y:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Trong đoạn script trên, bạn có thể thấy rõ rằng y = 2n, tuy nhiên, đầu ra là tuyến tính và trông giống như sau:

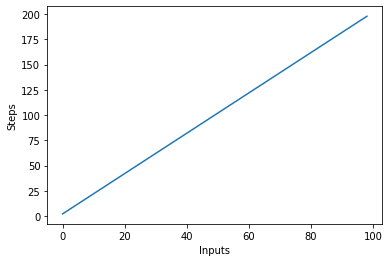
Độ phức tạp bậc hai - O (n²)

Độ phức tạp của một thuật toán được cho là bậc hai khi các bước cần thiết để thực hiện một thuật toán là một hàm bậc hai của số lượng mục trong đầu vào. Độ phức tạp bậc hai được biểu thị là O (n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Chúng ta có một vòng lặp bên ngoài lặp qua tất cả các mục trong danh sách đầu vào và sau đó là một vòng lặp bên trong lồng nhau, lặp lại qua tất cả các mục trong danh sách đầu vào. Tổng số bước được thực hiện là n * n, trong đó n là số mục trong mảng đầu vào.

Biểu đồ sau vẽ biểu đồ số lượng đầu vào theo các bước cho một thuật toán có độ phức tạp bậc hai:

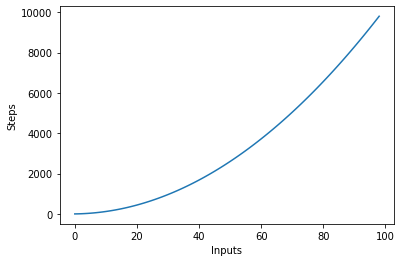
Độ phức hợp lôgarit - O (logn)

Một số thuật toán đạt được độ phức tạp lôgarit, chẳng hạn như Tìm kiếm nhị phân. Tìm kiếm nhị phân tìm kiếm một phần tử trong một mảng, bằng cách đánh dấu vào trung tâm của một mảng và cắt bớt một nửa trong đó phần tử không có. Nó làm điều này một lần nữa cho nửa còn lại và tiếp tục các bước tương tự cho đến khi phần tử được tìm thấy. Trong mỗi bước, nó một nửa số phần tử trong mảng.

Điều này yêu cầu mảng phải được sắp xếp và để chúng tôi đưa ra giả định về dữ liệu (chẳng hạn như nó được sắp xếp).

Khi bạn có thể đưa ra các giả định về dữ liệu đến, bạn có thể thực hiện các bước để giảm độ phức tạp của thuật toán. Độ phức tạp lôgarit là có thể mong muốn, vì nó đạt được hiệu suất tốt ngay cả với đầu vào có tỷ lệ cao.

Tìm sự phức tạp của các hàm phức hợp?

Trong các ví dụ trước, chúng ta có các hàm khá đơn giản trên đầu vào. Tuy nhiên, làm cách nào để tính toán Big-O của các hàm gọi (nhiều) hàm khác trên đầu vào?

Hãy xem:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

Trong tập lệnh ở trên, một số tác vụ đang được thực hiện, đầu tiên, một chuỗi được in 5 lần trên bảng điều khiển bằng cách sử dụng print bản tường trình. Tiếp theo, chúng tôi in danh sách đầu vào hai lần trên màn hình, và cuối cùng, một chuỗi khác được in ba lần trên bảng điều khiển. Để tìm độ phức tạp của một thuật toán như vậy, chúng ta cần chia nhỏ mã thuật toán thành các phần và cố gắng tìm độ phức tạp của các phần riêng lẻ. Đánh dấu mức độ phức tạp của mỗi phần.

Trong phần đầu tiên, chúng tôi có:

for i in range(5):
	print("Python is awesome")

Sự phức tạp của phần này là O (5) vì năm bước không đổi đang được thực hiện trong đoạn mã này bất kể đầu vào là gì.

Tiếp theo, chúng tôi có:

for item in items:
	print(item)

Chúng tôi biết độ phức tạp của đoạn mã trên là O (n). Tương tự, độ phức tạp của đoạn mã sau cũng O (n):

for item in items:
	print(item)

Cuối cùng, trong đoạn mã sau, một chuỗi được in ba lần, do đó độ phức tạp là O (3):

print("Big O")
print("Big O")
print("Big O")

Để tìm độ phức tạp tổng thể, chúng tôi chỉ cần thêm các độ phức tạp riêng lẻ sau:

O(5) + O(n) + O(n) + O(3)

Đơn giản hóa những điều trên chúng ta nhận được:

O(8) + O(2n) = O(8+2n)

Chúng tôi đã nói trước đó rằng khi đầu vào (có độ dài n trong trường hợp này) trở nên cực kỳ lớn, các hằng số trở nên không đáng kể tức là hai lần hoặc một nửa của vô cực vẫn ở vô cùng. Do đó, chúng ta có thể bỏ qua các hằng số. Độ phức tạp cuối cùng của thuật toán sẽ là O (n)!

Tệ nhất so với độ phức tạp của trường hợp tốt nhất

Thông thường, khi ai đó hỏi bạn về độ phức tạp của một thuật toán - họ quan tâm đến độ phức tạp trong trường hợp xấu nhất (Big-O). Đôi khi, họ cũng có thể quan tâm đến độ phức tạp trong trường hợp tốt nhất (Big-Omega).

Để hiểu mối quan hệ giữa những điều này, chúng ta hãy xem một đoạn mã khác:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

Trong đoạn mã ở trên, chúng ta có một hàm lấy một số và danh sách các số làm đầu vào. Nó trả về true nếu số đã qua được tìm thấy trong danh sách các số, ngược lại, nó trả về None. Nếu bạn tìm kiếm 2 trong danh sách, nó sẽ được tìm thấy trong lần so sánh đầu tiên. Đây là trường hợp phức tạp tốt nhất của thuật toán trong đó mục được tìm kiếm được tìm thấy trong chỉ mục được tìm kiếm đầu tiên. Trường hợp phức tạp tốt nhất, trong trường hợp này, là O (1). Mặt khác, nếu bạn tìm kiếm 10, nó sẽ được tìm thấy ở chỉ mục được tìm kiếm cuối cùng. Thuật toán sẽ phải tìm kiếm qua tất cả các mục trong danh sách, do đó sự phức tạp trong trường hợp xấu nhất trở thành O (n).

Ngoài độ phức tạp của trường hợp tốt nhất và xấu nhất, bạn cũng có thể tính toán độ phức tạp trung bình (Big-Theta) của một thuật toán, cho bạn biết “đã cho một đầu vào ngẫu nhiên, độ phức tạp thời gian mong đợi của thuật toán là bao nhiêu”?

Không gian phức tạp

Ngoài độ phức tạp về thời gian, nơi bạn đếm số bước cần thiết để hoàn thành việc thực thi một thuật toán, bạn cũng có thể tìm thấy không gian phức tạp đề cập đến lượng không gian bạn cần phân bổ trong bộ nhớ trong quá trình thực thi một chương trình.

Hãy xem ví dụ sau:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

Sản phẩm return_squares() hàm chấp nhận một danh sách các số nguyên và trả về một danh sách với các ô vuông tương ứng. Thuật toán phải cấp phát bộ nhớ cho cùng một số mục như trong danh sách đầu vào. Do đó, độ phức tạp không gian của thuật toán trở thành O (n).

Kết luận

Ký hiệu Big-O là số liệu tiêu chuẩn được sử dụng để đo độ phức tạp của một thuật toán. Trong hướng dẫn này, chúng tôi đã nghiên cứu ký hiệu Big-O là gì và cách nó có thể được sử dụng để đo độ phức tạp của nhiều thuật toán. Chúng tôi cũng đã nghiên cứu các loại hàm Big-O khác nhau với sự trợ giúp của các ví dụ Python khác nhau. Cuối cùng, chúng tôi đã xem xét ngắn gọn độ phức tạp của trường hợp xấu nhất và tốt nhất cùng với độ phức tạp về không gian.