使用 Python 示例进行大 O 表示法和算法分析

介绍

通常有多种方法可以使用计算机程序解决问题。 例如，有几种方法可以对数组中的项目进行排序——你可以使用 合并排序, 气泡排序, 插入排序， 等等。 所有这些算法都有自己的优缺点，开发人员的工作是权衡它们，以便能够选择在任何用例中使用的最佳算法。 换句话说，主要问题是当问题存在多种解决方案时，使用哪种算法来解决特定问题。

算法分析 是指分析不同算法的复杂性并找到最有效的算法来解决手头的问题。 大 O 符号 是用于描述算法复杂性的统计量度。

在本指南中，我们将首先简要回顾算法分析，然后深入了解 Big-O 表示法。 我们将看到如何在不同 Python 函数的帮助下使用 Big-O 表示法来查找算法复杂度。

为什么算法分析很重要？

为了理解为什么算法分析很重要，我们将借助一个简单的例子。 假设一个经理给他的两个员工一个任务，让他用 Python 设计一个算法，计算用户输入的数字的阶乘。 第一个员工开发的算法是这样的：

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

请注意，该算法只是将整数作为参数。 在 - 的里面 fact() 函数一个名为的变量 product 被初始化为 1. 一个循环从 1 至 n 并且在每次迭代期间， product 乘以循环迭代的数字，结果存储在 product 又变了。 循环执行后， product 变量将包含阶乘。

同样，第二名员工也开发了一种算法来计算一个数字的阶乘。 第二个员工使用递归函数计算数字的阶乘 n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

经理必须决定使用哪种算法。 为此，他们决定选择运行速度更快的算法。 一种方法是找出在相同输入上执行代码所需的时间。

在 Jupyter 笔记本中，您可以使用 %timeit 文字后跟函数调用以查找函数执行所花费的时间：

%timeit fact(50)

这将给我们：

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

输出表明该算法采用 9微秒 （加/减 45 纳秒）每个循环。

同样，我们可以计算第二种方法执行所需的时间：

%timeit fact2(50)

这将导致：

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

涉及递归的第二种算法采用 15微秒 （加/减 427 纳秒）。

执行时间表明，与涉及递归的第二个算法相比，第一个算法更快。 在处理大量输入时，性能差异会变得更加显着。

但是，执行时间不是衡量算法复杂性的好指标，因为它取决于硬件。 需要一个更客观的算法复杂度分析指标。 这就是 大O符号 来玩。

使用 Big-O 表示法的算法分析

Big-O 表示法表示算法的输入与执行算法所需的步骤之间的关系。 它由一个大“O”表示，后跟一个左括号和右括号。 在括号内，输入与算法所采取的步骤之间的关系使用“n”表示。

关键的一点是——Big-O 对 特别 运行算法的实例，例如 fact(50)，而是，它的表现如何 规模 给定增加的输入。 这是一个比具体实例的具体时间更好的评估指标！

例如，如果有一个 线性关系 在输入和算法完成其执行所采取的步骤之间，使用的 Big-O 表示法将是 O（N）. 同样，Big-O 表示法 二次函数 is O(n²).

建立直觉：

• O（N）： 在 n=1, 采取 1 步。 在 n=10, 10 个步骤。
• O(n²)： 在 n=1, 采取 1 步。 在 n=10, 100 个步骤。

At n=1，这两个会执行相同的！ 这就是为什么观察输入和处理该输入的步骤数之间的关系比仅仅评估具有一些具体输入的函数更好的另一个原因。

以下是一些最常见的 Big-O 函数：

名字	大O.
常数	O（c）
线性推力器	O（N）
二次	O(n²)
立方体	O(nXNUMX)
指数	O(2ⁿ)
对数	O（log（n））
对数线性	O(nlog(n))

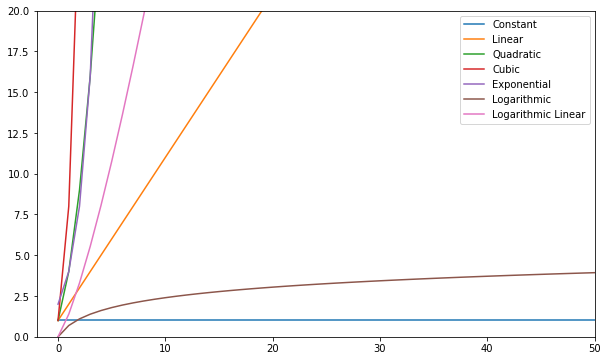
您可以可视化这些函数并进行比较：

一般来说——任何比线性差的东西都被认为是一种糟糕的复杂性（即低效），如果可能的话应该避免。 线性复杂性是可以的，通常是必要的邪恶。 对数很好。 常数是惊人的！

要了解如何计算 Big-O，让我们看一些常数、线性和二次复杂度的示例。

恒定的复杂性—— 氧(C)

如果完成算法执行所需的步骤保持不变，而与输入的数量无关，则称算法的复杂性是不变的。 常数复杂度表示为 O（c） 哪里 c 可以是任何常数。

让我们用 Python 编写一个简单的算法，找出列表中第一项的平方，然后将其打印到屏幕上：

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

在上面的脚本中， 与输入大小无关，或输入列表中的项目数 items，该算法只执行 2 个步骤：

1. 找到第一个元素的平方
2. 在屏幕上打印结果。

因此，复杂性保持不变。

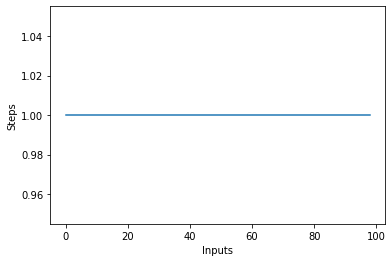
如果你绘制一个不同大小的线图 items 在 X 轴上输入，在 Y 轴上输入步数，你会得到一条直线。 让我们创建一个简短的脚本来帮助我们将其可视化。 无论输入的数量如何，执行的步骤数都保持不变：

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

线性复杂度—— O（N）

如果完成算法执行所需的步骤随输入的数量线性增加或减少，则称算法的复杂性是线性的。 线性复杂度表示为 O（N）.

在这个例子中，让我们编写一个简单的程序，将列表中的所有项目显示到控制台：

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

复杂的 linear_algo() 在上面的例子中函数是线性的，因为 for 循环的迭代次数将是 等于输入的大小 items 排列. 例如，如果有 4 个项目 items 列表中，for循环将被执行4次。

让我们快速创建线性复杂度算法的图，其中 x 轴上的输入数和 y 轴上的步数：

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

这将导致：

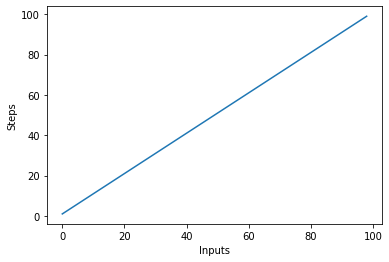
需要注意的重要一点是，随着大量输入，常量往往会失去价值。 这就是为什么我们通常会从 Big-O 表示法中删除常量，并且像 O(2n) 这样的表达式通常会缩短为 O(n)。 O(2n) 和 O(n) 都是线性的——重要的是线性关系，而不是具体值。 例如，让我们修改 linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

有两个迭代输入的 for 循环 items 列表。 因此算法的复杂度变为 O（2n），但是在输入列表中有无限项的情况下，无穷大的两倍仍然等于无穷大。 我们可以忽略常数 2 （因为它最终是微不足道的）并且算法的复杂性仍然存在 O（N）.

让我们通过在 X 轴上绘制输入和在 Y 轴上绘制步数来可视化这个新算法：

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

在上面的脚本中，您可以清楚地看到 y=2n，但是，输出是线性的，如下所示：

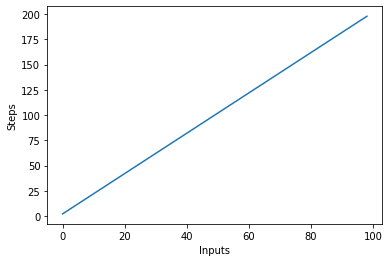
二次复杂度 – O(n²)

当执行算法所需的步骤是输入项数的二次函数时，算法的复杂性被称为二次函数。 二次复杂度表示为 O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

我们有一个外循环遍历输入列表中的所有项目，然后是一个嵌套的内循环，它再次遍历输入列表中的所有项目。 执行的总步数为 n*n，其中 n 是输入数组中的项目数。

下图绘制了输入数量与具有二次复杂度的算法的步骤：

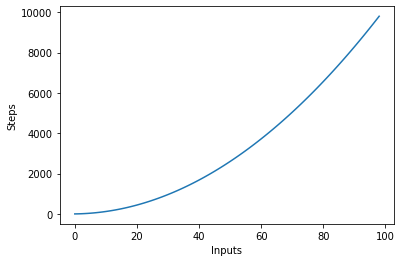
对数复杂度 – O（登录）

一些算法实现对数复杂度，例如 二进制搜索. 二分搜索通过检查数组中的元素 中间 数组，并修剪元素不在的一半。 它对剩余的一半再次执行此操作，并继续执行相同的步骤，直到找到该元素。 在每一步中，它 半 数组中的元素数。

这需要对数组进行排序，并让我们对数据做出假设（例如它已排序）。

当您可以对传入数据做出假设时，您可以采取措施降低算法的复杂性。 对数复杂度是可取的，因为即使在高度缩放的输入下也能实现良好的性能。

寻找复杂函数的复杂性？

在前面的例子中，我们有相当简单的输入函数。 但是，我们如何计算在输入上调用（多个）其他函数的函数的 Big-O？

让我们来看看：

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

在上面的脚本中，正在执行几个任务，首先，在控制台上打印一个字符串 5 次，使用 print 陈述。 接下来，我们在屏幕上打印两次输入列表，最后在控制台上打印三次另一个字符串。 要找出这种算法的复杂性，我们需要将算法代码分解成几部分，并尝试找出各个部分的复杂性。 记下每件作品的复杂性。

在第一部分中，我们有：

for i in range(5):
	print("Python is awesome")

这部分的复杂度是 O（5） 因为无论输入如何，这段代码都在执行五个恒定步骤。

接下来，我们有：

for item in items:
	print(item)

我们知道上面这段代码的复杂度是 O（N）. 同样，下面这段代码的复杂度也是 O（N）:

for item in items:
	print(item)

最后，在下面这段代码中，一个字符串被打印了 XNUMX 次，因此复杂度为 O（3）:

print("Big O")
print("Big O")
print("Big O")

要找到整体复杂性，我们只需添加这些单独的复杂性：

O(5) + O(n) + O(n) + O(3)

简化上面我们得到：

O(8) + O(2n) = O(8+2n)

我们之前说过，当输入（在这种情况下长度为 n）变得非常大时，常数变得无关紧要，即无穷大的两倍或一半仍然保持无穷大。 因此，我们可以忽略常量。 算法的最终复杂度为 O（N）!

最坏与最佳情况的复杂性

通常，当有人问你算法的复杂性时——他们对最坏情况的复杂性（Big-O）感兴趣。 有时，他们可能也对最佳情况复杂性（Big-Omega）感兴趣。

要理解它们之间的关系，我们来看另一段代码：

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

在上面的脚本中，我们有一个函数，它接受一个数字和一个数字列表作为输入。 如果在数字列表中找到传递的数字，则返回 true，否则返回 None. 如果在列表中搜索 2，将在第一个比较中找到。 这是算法的最佳情况复杂度，因为在第一个搜索索引中找到了搜索项。 最佳案例复杂度，在这种情况下，是 O（1）. 另一方面，如果您搜索 10，它将在最后搜索的索引处找到。 该算法必须搜索列表中的所有项目，因此 最坏情况复杂度 成为 O（N）.

除了最佳和最坏情况复杂度，您还可以计算 平均复杂度 （Big-Theta）算法，它告诉你“给定一个随机输入，算法的预期时间复杂度是多少”？

空间复杂度

除了计算完成算法执行所需的步骤数的时间复杂度之外，您还可以找到 空间复杂度 它指的是在程序执行期间您需要在内存中分配的空间量。

看看下面的例子：

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

return_squares() 函数接受一个整数列表并返回一个带有相应正方形的列表。 该算法必须为与输入列表中相同数量的项目分配内存。 因此，算法的空间复杂度变为 O（N）.

结论

Big-O 表示法是用于衡量算法复杂性的标准度量。 在本指南中，我们研究了什么是 Big-O 表示法以及如何使用它来衡量各种算法的复杂性。 我们还借助不同的 Python 示例研究了不同类型的 Big-O 函数。 最后，我们简要回顾了最坏和最好的情况复杂度以及空间复杂度。