1Max-Planck-InstitutfürQuantenoptik,Hans-Kopfermann-Straße1,85748 Garching,Germany
2慕尼黑量子科学技术中心,Schellingstraße 4, 80799 München, Germany
3维也纳大学数学学院,Oskar-Morgenstern-Platz 1, 1090 Wien, Austria
4维也纳大学物理系,Boltzmanngasse 5, 1090 Wien, Austria
觉得本文有趣或想讨论? 在SciRate上发表评论或发表评论.
抽象
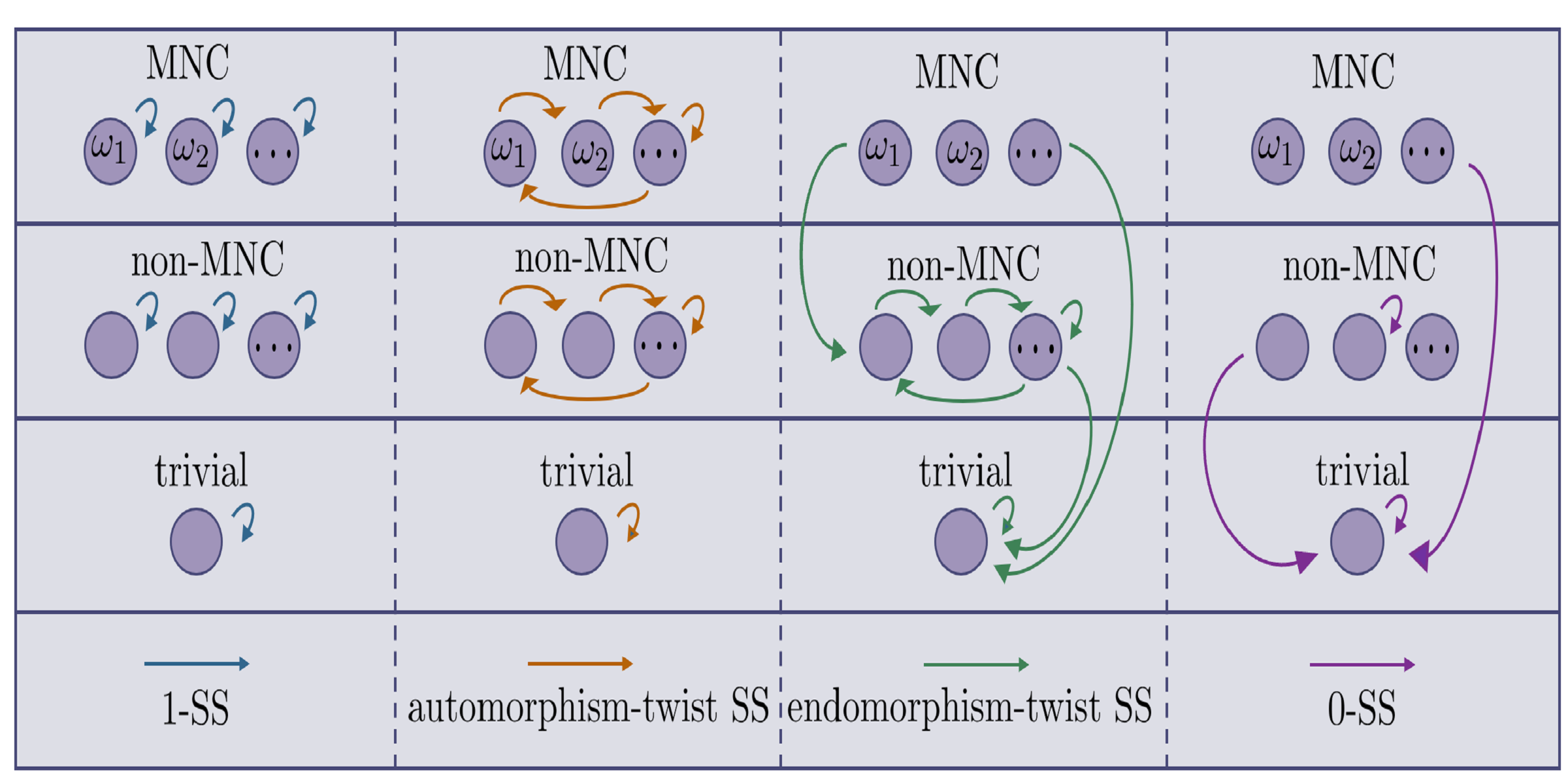
我们通过研究弦序参数和其他探针在噪声通道下的演化,系统地研究了开放量子系统中对称保护拓扑 (SPT) 序的稳健性。 我们发现一维 SPT 阶对与满足强对称条件的环境的噪声耦合具有鲁棒性,而它会因仅满足弱对称条件的噪声而不稳定,这概括了封闭系统的对称概念。 我们还讨论了在满足强对称条件的扭曲版本的嘈杂通道下,SPT 阶段到其他具有相同或更小复杂度的 SPT 阶段的“转变”。
►BibTeX数据
►参考
[1] FDM 霍尔丹。 “一维海森堡反铁磁体的连续动力学:用 $o(1)$ 非线性西格玛模型进行识别”。 物理快报 A 3, 93–464 (468)。
https://doi.org/10.1016/0375-9601(83)90631-X
[2] FDM 霍尔丹。 “大自旋海森堡反铁磁体的非线性场论:一维易轴 néel 态的半经典量子化孤子”。 物理。 牧师莱特。 50, 1153–1156 (1983)。
https:/ / doi.org/ 10.1103 / PhysRevLett.50.1153
[3] 伊恩·阿弗莱克、汤姆·肯尼迪、埃利奥特·H·利布和哈尔·塔萨基。 “反铁磁体中价键基态的严格结果”。 物理。 牧师莱特。 59, 799–802 (1987)。
https:/ / doi.org/ 10.1103 / PhysRevLett.59.799
[4] Marcel den Nijs 和 Koos Rommelse。 “晶体表面的预粗糙化转变和量子自旋链中的价键相”。 物理。 修订版 B 40, 4709–4734 (1989)。
https:/ / doi.org/ 10.1103 / PhysRevB.40.4709
[5] 汤姆·肯尼迪和哈尔·塔萨基。 “haldane 间隙反铁磁体中隐藏的 $mathbb{Z}_2timesmathbb{Z}_2$ 对称性破缺”。 物理。 修订版 B 45, 304–307 (1992)。
https:/ / doi.org/ 10.1103 / PhysRevB.45.304
[6] Frank Pollmann 和 Ari M. Turner。 “一维对称保护拓扑相的检测”。 物理。 修订版 B 86, 125441 (2012)。
https:/ / doi.org/ 10.1103 / PhysRevB.86.125441
[7] F. Pollmann、AM Turner、E. Berg 和 M. Oshikawa。 “一维拓扑相的纠缠谱”。 物理。 修订版 B 81, 064439 (2010)。 arXiv:0910.1811。
https:/ / doi.org/ 10.1103 / PhysRevB.81.064439
的arXiv:0910.1811
[8] 乌尔里希·绍尔沃克。 “矩阵乘积态时代的密度矩阵重整化群”。 物理学年鉴 326, 96–192 (2011)。
https:/ / doi.org/ 10.1016 / j.aop.2010.09.012
[9] Ignacio Cirac、David Perez-Garcia、Norbert Schuch 和 Frank Verstraete。 “矩阵乘积状态和投影纠缠对状态:概念、对称性和定理”。 牧师国防部。 物理。 93, 045003 (2021)。 arXiv:2011.12127。
https:/ / doi.org/ 10.1103 / PhysRevD.103.015030
的arXiv:2011.1212
[10] MB黑斯廷斯。 “一维量子系统的面积定律”。 统计力学杂志:理论与实验 2007,P08024–P08024 (2007)。
https://doi.org/10.1088/1742-5468/2007/08/p08024
[11] F. Verstraete 和 JI Cirac。 “矩阵乘积状态忠实地代表了基态”。 物理。 修订版 B 73, 094423 (2006)。 arXiv:条件垫/0505140。
https:/ / doi.org/ 10.1103 / PhysRevB.73.094423
arXiv:cond-mat / 0505140
[12] Norbert Schuch、Michael M. Wolf、Frank Verstraete 和 J. Ignacio Cirac。 “矩阵乘积状态的熵缩放和可模拟性”。 物理。 牧师莱特。 100, 30504 (2008)。 arXiv:0705.0292。
https:/ / doi.org/ 10.1103 / PhysRevLett.100.030504
的arXiv:0705.0292
[13] Andras Molnar、José Garre-Rubio、David Pérez-García、Norbert Schuch 和 J. Ignacio Cirac。 “产生相同状态的正常投影纠缠对状态”。 新 J. Phys。 20, 113017 (2018). arXiv:1804.04964。
https://doi.org/10.1088/1367-2630/aae9fa
的arXiv:1804.0496
[14] Frank Pollmann、Erez Berg、Ari M. Turner 和 Masaki Oshikawa。 “一维量子自旋系统中拓扑相的对称保护”。 物理。 修订版 B 85, 075125 (2012)。
https:/ / doi.org/ 10.1103 / PhysRevB.85.075125
[15] 谢晨、顾政成和温晓刚。 “一维自旋系统中间隙对称相的分类”。 物理。 修订版 B 83, 035107 (2011)。
https:/ / doi.org/ 10.1103 / PhysRevB.83.035107
[16] Norbert Schuch、David Pérez-García 和 Ignacio Cirac。 “使用矩阵乘积状态和投影纠缠对状态对量子相进行分类”。 物理。 修订版 B 84, 165139 (2011)。
https:/ / doi.org/ 10.1103 / PhysRevB.84.165139
[17] Xie Chen、Zheng-Cheng Gu、Zheng-Xin Liu 和 Xiao-Gang Wen。 “对称性保护相互作用的玻色子系统中的拓扑顺序”。 科学 338, 1604 (2012)。 arXiv:1301.0861。
的arXiv:1301.0861
[18] 罗伯特·劳森多夫、谢尔盖·布拉维和吉姆·哈林顿。 “嘈杂簇态中的远程量子纠缠”。 物理。 修订版 A 71, 062313 (2005)。
https:/ / doi.org/ 10.1103 / PhysRevA.71.062313
[19] 马修 B. 黑斯廷斯。 “非零温度下的拓扑序”。 物理评论快报 107 (2011)。
https:///doi.org/10.1103/physrevlett.107.210501
[20] Sam Roberts、Beni Yoshida、Aleksander Kubica 和 Stephen D. Bartlett。 “非零温度下的对称保护拓扑序”。 物理评论 A 96 (2017)。
https:///doi.org/10.1103/physreva.96.022306
[21] Sebastian Diehl、Enrique Rico、Mikhail A. Baranov 和 Peter Zoller。 “原子量子线耗散拓扑”。 自然物理学 7, 971–977 (2011)。
https:/ / doi.org/ 10.1038 / nphys2106
[22] CE Bardyn、MA Baranov、CV Kraus、E Rico、A İmamoğlu、P Zoller 和 S Diehl。 “耗散拓扑”。 新物理杂志 15, 085001 (2013).
https://doi.org/10.1088/1367-2630/15/8/085001
[23] B. Kraus、HP Büchler、S. Diehl、A. Kantian、A. Micheli 和 P. Zoller。 “通过量子马尔可夫过程制备纠缠态”。 物理评论 A 78 (2008)。
https:///doi.org/10.1103/physreva.78.042307
[24] Leo Zhou、Soonwon Choi 和 Mikhail D. Lukin。 “矩阵乘积态的对称保护耗散制备”(2017 年)。 arXiv:1706.01995。
https:/ / doi.org/ 10.1103 / PhysRevA.104.032418
的arXiv:1706.01995
[25] Simon Lieu、Ron Belyansky、Jeremy T. Young、Rex Lundgren、Victor V. Albert 和 Alexey V. Gorshkov。 “开放量子系统中的对称破缺和纠错”。 物理。 牧师莱特。 125, 240405 (2020)。
https:/ / doi.org/ 10.1103 / PhysRevLett.125.240405
[26] 维克多诉艾伯特。 “具有多个稳态的 Lindbladians:理论与应用”(2018 年)。 arXiv:1802.00010。
的arXiv:1802.00010
[27] Berislav Buča 和 Tomaž Prosen。 “关于林德布拉德方程对称性约简的说明:受限开放自旋链中的传输”。 新物理杂志 14, 073007 (2012).
https://doi.org/10.1088/1367-2630/14/7/073007
[28] Victor V. Albert 和梁江。 “lindblad 主方程中的对称性和守恒量”。 物理。 修订版 A 89, 022118 (2014)。
https:/ / doi.org/ 10.1103 / PhysRevA.89.022118
[29] Simon Lieu、Ron Belyansky、Jeremy T. Young、Rex Lundgren、Victor V. Albert 和 Alexey V. Gorshkov。 “开放量子系统中的对称性破缺和纠错”。 物理评论快报 125 (2020)。
https:///doi.org/10.1103/physrevlett.125.240405
[30] Andrea Coser 和 David Pérez-García。 “通过快速耗散演化对混合状态进行阶段分类”。 量子 3, 174 (2019)。
https://doi.org/10.22331/q-2019-08-12-174
[31] F. Verstraete 和 JI Cirac。 “矩阵乘积状态忠实地代表了基态”。 物理。 修订版 B 73, 094423 (2006)。
https:/ / doi.org/ 10.1103 / PhysRevB.73.094423
[32] Jacob Biamonte 和 Ville Bergholm。 “简而言之张量网络”(2017 年)。 arXiv:1708.00006。
的arXiv:1708.00006
[33] 罗曼·奥鲁斯。 “张量网络实用介绍:矩阵乘积状态和投影纠缠对状态”。 物理学年鉴 349, 117–158 (2014)。
https:/ / doi.org/ 10.1016 / j.aop.2014.06.013
[34] Jacob C. Bridgeman 和 Christopher T. Chubb。 “挥手和诠释舞蹈:张量网络入门课程”。 J.物理学。 答:数学。 理论。 50(2017 年)。 arXiv:1603.03039。
https://doi.org/10.1088/1751-8121/aa6dc3
的arXiv:1603.0303
[35] D. Perez-Garcia、F. Verstraete、MM Wolf 和 JI Cirac。 “矩阵乘积状态表示”。 量子信息。 电脑。 7, 401–430 (2007)。
https://doi.org/10.48550/arXiv.quant-ph/0608197
arXiv:quant-ph / 0608197
[36] Michael A. Nielsen 和 Isaac L. Chuang。 “量子计算与量子信息:10 周年纪念版”。 剑桥大学出版社。 (2010)。
[37] 迈克尔·沃尔夫。 “量子通道和操作:导览”(2012 年)。
[38] 朱利亚诺·贝内蒂、朱利奥·卡萨蒂和朱利亚诺·斯特里尼。 “量子计算和信息原理”。 世界科学。 (2004)。 arXiv:https:/ / www.worldscientific.com/ doi/ pdf/ 10.1142/ 5528。
https:/ / doi.org/10.1142/ 5528
arXiv:https://www.worldscientific.com/doi/pdf/10.1142/5528
[39] W. 富尔顿和 J. 哈里斯。 “表示论:第一门课程”。 施普林格纽约。 (2013)。 网址:books.google.de/ books?id=6TwmBQAAQBAJ。
https://books.google.de/books?id=6TwmBQAAQBAJ
[40] Heinz-Peter Breuer 和 Francesco Petruccione。 “开放量子系统理论”。 牛津大学出版社。 (2007)。
https:///doi.org/10.1093/acprof:oso / 9780199213900.001.0001
[41] Jutho Haegeman、David Pérez-García、Ignacio Cirac 和 Norbert Schuch。 “一维对称保护相的有序参数”。 物理评论快报 109 (2012)。
https:///doi.org/10.1103/physrevlett.109.050402
[42] Ken Shiozaki 和Shinsei Ryu。 “(1+1) 维玻色子对称保护拓扑相的矩阵乘积状态和等变拓扑场论”。 J. 高能量。 物理。 100(2017 年)。
https:/ / doi.org/ 10.1007 / JHEP04(2017)100
[43] Anton Kapustin、Alex Turzillo 和 Minyoung You。 “拓扑场论和矩阵乘积状态”。 物理。 修订版 B 96, 075125 (2017)。
https:/ / doi.org/ 10.1103 / PhysRevB.96.075125
[44] Dominic V Else、Stephen D Bartlett 和 Andrew C Doherty。 “基态下基于测量的量子计算的对称性保护”。 新物理杂志 14, 113016 (2012).
https://doi.org/10.1088/1367-2630/14/11/113016
[45] Caroline de Groot、David T Stephen、Andras Molnar 和 Norbert Schuch。 “对称保护拓扑相中难以接近的纠缠”。 物理学杂志 A:数学与理论 53, 335302 (2020).
https://doi.org/10.1088/1751-8121/ab98c7
[46] IAG Berkovich、LS Kazarin 和 EM Zhmud。 “有限群的特征”。 德格鲁伊特。 (2018)。
[47] Lorenzo Piroli 和 J. Ignacio Cirac。 “量子元胞自动机、张量网络和面积定律”。 物理。 牧师莱特。 125, 190402 (2020)。
https:/ / doi.org/ 10.1103 / PhysRevLett.125.190402
[48] J Ignacio Cirac、David Perez-Garcia、Norbert Schuch 和 Frank Verstraete。 “矩阵乘积幺正:结构、对称性和拓扑不变量”。 统计力学杂志:理论与实验 2017, 083105 (2017).
https://doi.org/10.1088/1742-5468/aa7e55
[49] M. Burak Şahinoğlu、Sujeet K. Shukla、Feng Bi 和 Xie Chen。 “保局酉元的矩阵乘积表示”。 物理。 修订版 B 98, 245122 (2018)。
https:/ / doi.org/ 10.1103 / PhysRevB.98.245122
[50] D. Gross、V. Nesme 和 H. Vogts。 “一维量子行走和元胞自动机的索引论”。 公社。 数学。 物理。 310、419–454(2012 年)。
https://doi.org/10.1007/s00220-012-1423-1
[51] Zongping Gong、Christoph Sünderhauf、Norbert Schuch 和 J. Ignacio Cirac。 “具有对称性的矩阵乘积酉分类”。 物理。 牧师莱特。 124、100402(2020 年)。
https:/ / doi.org/ 10.1103 / PhysRevLett.124.100402
[52] David T. Stephen、Dong-Sheng Wang、Abhishodh Prakash、Tzu-Chieh Wei 和 Robert Raussendorf。 “对称保护拓扑相的计算能力”。 物理评论快报 119 (2017)。
https:///doi.org/10.1103/physrevlett.119.010504
[53] Adam Smith、MS Kim、Frank Pollmann 和 Johannes Knolle。 “在当前数字量子计算机上模拟量子多体动力学”。 npj 量子信息 5 (2019)。
https://doi.org/10.1038/s41534-019-0217-0
[54] Daniel Azses、Rafael Haenel、Yehuda Naveh、Robert Raussendorf、Eran Sela 和 Emanuele G. Dalla Torre。 “在嘈杂的量子计算机上识别受对称保护的拓扑状态”。 物理。 牧师莱特。 125、120502(2020 年)。
https:/ / doi.org/ 10.1103 / PhysRevLett.125.120502
[1] FDM 霍尔丹。 “一维海森堡反铁磁体的连续动力学:用 $o(1)$ 非线性西格玛模型进行识别”。 物理快报 A 3, 93–464 (468)。
https://doi.org/10.1016/0375-9601(83)90631-X
[2] FDM 霍尔丹。 “大自旋海森堡反铁磁体的非线性场论:一维易轴 néel 态的半经典量子化孤子”。 物理。 牧师莱特。 50, 1153–1156 (1983)。
https:/ / doi.org/ 10.1103 / PhysRevLett.50.1153
[3] 伊恩·阿弗莱克、汤姆·肯尼迪、埃利奥特·H·利布和哈尔·塔萨基。 “反铁磁体中价键基态的严格结果”。 物理。 牧师莱特。 59, 799–802 (1987)。
https:/ / doi.org/ 10.1103 / PhysRevLett.59.799
[4] Marcel den Nijs 和 Koos Rommelse。 “晶体表面的预粗糙化转变和量子自旋链中的价键相”。 物理。 修订版 B 40, 4709–4734 (1989)。
https:/ / doi.org/ 10.1103 / PhysRevB.40.4709
[5] 汤姆·肯尼迪和哈尔·塔萨基。 “haldane 间隙反铁磁体中隐藏的 $mathbb{Z}_2timesmathbb{Z}_2$ 对称性破缺”。 物理。 修订版 B 45, 304–307 (1992)。
https:/ / doi.org/ 10.1103 / PhysRevB.45.304
[6] Frank Pollmann 和 Ari M. Turner。 “一维对称保护拓扑相的检测”。 物理。 修订版 B 86, 125441 (2012)。
https:/ / doi.org/ 10.1103 / PhysRevB.86.125441
[7] F. Pollmann、AM Turner、E. Berg 和 M. Oshikawa。 “一维拓扑相的纠缠谱”。 物理。 修订版 B 81, 064439 (2010)。 arXiv:0910.1811。
https:/ / doi.org/ 10.1103 / PhysRevB.81.064439
的arXiv:0910.1811
[8] 乌尔里希·绍尔沃克。 “矩阵乘积态时代的密度矩阵重整化群”。 物理学年鉴 326, 96–192 (2011)。
https:/ / doi.org/ 10.1016 / j.aop.2010.09.012
[9] Ignacio Cirac、David Perez-Garcia、Norbert Schuch 和 Frank Verstraete。 “矩阵乘积状态和投影纠缠对状态:概念、对称性和定理”。 牧师国防部。 物理。 93, 045003 (2021)。 arXiv:2011.12127。
的arXiv:2011.1212
[10] MB黑斯廷斯。 “一维量子系统的面积定律”。 统计力学杂志:理论与实验 2007,P08024–P08024 (2007)。
https://doi.org/10.1088/1742-5468/2007/08/p08024
[11] F. Verstraete 和 JI Cirac。 “矩阵乘积状态忠实地代表了基态”。 物理。 修订版 B 73, 094423 (2006)。 arXiv:条件垫/0505140。
arXiv:cond-mat / 0505140
[12] Norbert Schuch、Michael M. Wolf、Frank Verstraete 和 J. Ignacio Cirac。 “矩阵乘积状态的熵缩放和可模拟性”。 物理。 牧师莱特。 100, 30504 (2008)。 arXiv:0705.0292。
的arXiv:0705.0292
[13] Andras Molnar、José Garre-Rubio、David Pérez-García、Norbert Schuch 和 J. Ignacio Cirac。 “产生相同状态的正常投影纠缠对状态”。 新 J. Phys。 20, 113017 (2018). arXiv:1804.04964。
https://doi.org/10.1088/1367-2630/aae9fa
的arXiv:1804.0496
[14] Frank Pollmann、Erez Berg、Ari M. Turner 和 Masaki Oshikawa。 “一维量子自旋系统中拓扑相的对称保护”。 物理。 修订版 B 85, 075125 (2012)。
https:/ / doi.org/ 10.1103 / PhysRevB.85.075125
[15] 谢晨、顾政成和温晓刚。 “一维自旋系统中间隙对称相的分类”。 物理。 修订版 B 83, 035107 (2011)。
https:/ / doi.org/ 10.1103 / PhysRevB.83.035107
[16] Norbert Schuch、David Pérez-García 和 Ignacio Cirac。 “使用矩阵乘积状态和投影纠缠对状态对量子相进行分类”。 物理。 修订版 B 84, 165139 (2011)。
https:/ / doi.org/ 10.1103 / PhysRevB.84.165139
[17] Xie Chen、Zheng-Cheng Gu、Zheng-Xin Liu 和 Xiao-Gang Wen。 “对称性保护相互作用的玻色子系统中的拓扑顺序”。 科学 338, 1604 (2012)。 arXiv:1301.0861。
的arXiv:1301.0861
[18] 罗伯特·劳森多夫、谢尔盖·布拉维和吉姆·哈林顿。 “嘈杂簇态中的远程量子纠缠”。 物理。 修订版 A 71, 062313 (2005)。
https:/ / doi.org/ 10.1103 / PhysRevA.71.062313
[19] 马修 B. 黑斯廷斯。 “非零温度下的拓扑序”。 物理评论快报 107 (2011)。
https:///doi.org/10.1103/physrevlett.107.210501
[20] Sam Roberts、Beni Yoshida、Aleksander Kubica 和 Stephen D. Bartlett。 “非零温度下的对称保护拓扑序”。 物理评论 A 96 (2017)。
https:///doi.org/10.1103/physreva.96.022306
[21] Sebastian Diehl、Enrique Rico、Mikhail A. Baranov 和 Peter Zoller。 “原子量子线耗散拓扑”。 自然物理学 7, 971–977 (2011)。
https:/ / doi.org/ 10.1038 / nphys2106
[22] CE Bardyn、MA Baranov、CV Kraus、E Rico、A İmamoğlu、P Zoller 和 S Diehl。 “耗散拓扑”。 新物理杂志 15, 085001 (2013).
https://doi.org/10.1088/1367-2630/15/8/085001
[23] B. Kraus、HP Büchler、S. Diehl、A. Kantian、A. Micheli 和 P. Zoller。 “通过量子马尔可夫过程制备纠缠态”。 物理评论 A 78 (2008)。
https:///doi.org/10.1103/physreva.78.042307
[24] Leo Zhou、Soonwon Choi 和 Mikhail D. Lukin。 “矩阵乘积态的对称保护耗散制备”(2017 年)。 arXiv:1706.01995。
的arXiv:1706.01995
[25] Simon Lieu、Ron Belyansky、Jeremy T. Young、Rex Lundgren、Victor V. Albert 和 Alexey V. Gorshkov。 “开放量子系统中的对称破缺和纠错”。 物理。 牧师莱特。 125, 240405 (2020)。
https:/ / doi.org/ 10.1103 / PhysRevLett.125.240405
[26] 维克多诉艾伯特。 “具有多个稳态的 Lindbladians:理论与应用”(2018 年)。 arXiv:1802.00010。
的arXiv:1802.00010
[27] Berislav Buča 和 Tomaž Prosen。 “关于林德布拉德方程对称性约简的说明:受限开放自旋链中的传输”。 新物理杂志 14, 073007 (2012).
https://doi.org/10.1088/1367-2630/14/7/073007
[28] Victor V. Albert 和梁江。 “lindblad 主方程中的对称性和守恒量”。 物理。 修订版 A 89, 022118 (2014)。
https:/ / doi.org/ 10.1103 / PhysRevA.89.022118
[29] Simon Lieu、Ron Belyansky、Jeremy T. Young、Rex Lundgren、Victor V. Albert 和 Alexey V. Gorshkov。 “开放量子系统中的对称性破缺和纠错”。 物理评论快报 125 (2020)。
https:///doi.org/10.1103/physrevlett.125.240405
[30] Andrea Coser 和 David Pérez-García。 “通过快速耗散演化对混合状态进行阶段分类”。 量子 3, 174 (2019)。
https://doi.org/10.22331/q-2019-08-12-174
[31] F. Verstraete 和 JI Cirac。 “矩阵乘积状态忠实地代表了基态”。 物理。 修订版 B 73, 094423 (2006)。
https:/ / doi.org/ 10.1103 / PhysRevB.73.094423
[32] Jacob Biamonte 和 Ville Bergholm。 “简而言之张量网络”(2017 年)。 arXiv:1708.00006。
的arXiv:1708.00006
[33] 罗曼·奥鲁斯。 “张量网络实用介绍:矩阵乘积状态和投影纠缠对状态”。 物理学年鉴 349, 117–158 (2014)。
https:/ / doi.org/ 10.1016 / j.aop.2014.06.013
[34] Jacob C. Bridgeman 和 Christopher T. Chubb。 “挥手和诠释舞蹈:张量网络入门课程”。 J.物理学。 答:数学。 理论。 50(2017 年)。 arXiv:1603.03039。
https://doi.org/10.1088/1751-8121/aa6dc3
的arXiv:1603.0303
[35] D. Perez-Garcia、F. Verstraete、MM Wolf 和 JI Cirac。 “矩阵乘积状态表示”。 量子信息。 电脑。 7, 401–430 (2007)。
https://doi.org/10.48550/arXiv.quant-ph/0608197
arXiv:quant-ph / 0608197
[36] Michael A. Nielsen 和 Isaac L. Chuang。 “量子计算与量子信息:10 周年纪念版”。 剑桥大学出版社。 (2010)。
[37] 迈克尔·沃尔夫。 “量子通道和操作:导览”(2012 年)。
[38] 朱利亚诺·贝内蒂、朱利奥·卡萨蒂和朱利亚诺·斯特里尼。 “量子计算和信息原理”。 世界科学。 (2004)。 arXiv:https:/ / www.worldscientific.com/ doi/ pdf/ 10.1142/ 5528。
https:/ / doi.org/10.1142/ 5528
arXiv:https://www.worldscientific.com/doi/pdf/10.1142/5528
[39] W. 富尔顿和 J. 哈里斯。 “表示论:第一门课程”。 施普林格纽约。 (2013)。 网址:books.google.de/ books?id=6TwmBQAAQBAJ。
https://books.google.de/books?id=6TwmBQAAQBAJ
[40] Heinz-Peter Breuer 和 Francesco Petruccione。 “开放量子系统理论”。 牛津大学出版社。 (2007)。
https:///doi.org/10.1093/acprof:oso / 9780199213900.001.0001
[41] Jutho Haegeman、David Pérez-García、Ignacio Cirac 和 Norbert Schuch。 “一维对称保护相的有序参数”。 物理评论快报 109 (2012)。
https:///doi.org/10.1103/physrevlett.109.050402
[42] Ken Shiozaki 和Shinsei Ryu。 “(1+1) 维玻色子对称保护拓扑相的矩阵乘积状态和等变拓扑场论”。 J. 高能量。 物理。 100(2017 年)。
https:/ / doi.org/ 10.1007 / JHEP04(2017)100
[43] Anton Kapustin、Alex Turzillo 和 Minyoung You。 “拓扑场论和矩阵乘积状态”。 物理。 修订版 B 96, 075125 (2017)。
https:/ / doi.org/ 10.1103 / PhysRevB.96.075125
[44] Dominic V Else、Stephen D Bartlett 和 Andrew C Doherty。 “基态下基于测量的量子计算的对称性保护”。 新物理杂志 14, 113016 (2012).
https://doi.org/10.1088/1367-2630/14/11/113016
[45] Caroline de Groot、David T Stephen、Andras Molnar 和 Norbert Schuch。 “对称保护拓扑相中难以接近的纠缠”。 物理学杂志 A:数学与理论 53, 335302 (2020).
https://doi.org/10.1088/1751-8121/ab98c7
[46] IAG Berkovich、LS Kazarin 和 EM Zhmud。 “有限群的特征”。 德格鲁伊特。 (2018)。
[47] Lorenzo Piroli 和 J. Ignacio Cirac。 “量子元胞自动机、张量网络和面积定律”。 物理。 牧师莱特。 125, 190402 (2020)。
https:/ / doi.org/ 10.1103 / PhysRevLett.125.190402
[48] J Ignacio Cirac、David Perez-Garcia、Norbert Schuch 和 Frank Verstraete。 “矩阵乘积幺正:结构、对称性和拓扑不变量”。 统计力学杂志:理论与实验 2017, 083105 (2017).
https://doi.org/10.1088/1742-5468/aa7e55
[49] M. Burak Şahinoğlu、Sujeet K. Shukla、Feng Bi 和 Xie Chen。 “保局酉元的矩阵乘积表示”。 物理。 修订版 B 98, 245122 (2018)。
https:/ / doi.org/ 10.1103 / PhysRevB.98.245122
[50] D. Gross、V. Nesme 和 H. Vogts。 “一维量子行走和元胞自动机的索引论”。 公社。 数学。 物理。 310、419–454(2012 年)。
https://doi.org/10.1007/s00220-012-1423-1
[51] Zongping Gong、Christoph Sünderhauf、Norbert Schuch 和 J. Ignacio Cirac。 “具有对称性的矩阵乘积酉分类”。 物理。 牧师莱特。 124、100402(2020 年)。
https:/ / doi.org/ 10.1103 / PhysRevLett.124.100402
[52] David T. Stephen、Dong-Sheng Wang、Abhishodh Prakash、Tzu-Chieh Wei 和 Robert Raussendorf。 “对称保护拓扑相的计算能力”。 物理评论快报 119 (2017)。
https:///doi.org/10.1103/physrevlett.119.010504
[53] Adam Smith、MS Kim、Frank Pollmann 和 Johannes Knolle。 “在当前数字量子计算机上模拟量子多体动力学”。 npj 量子信息 5 (2019)。
https://doi.org/10.1038/s41534-019-0217-0
[54] Daniel Azses、Rafael Haenel、Yehuda Naveh、Robert Raussendorf、Eran Sela 和 Emanuele G. Dalla Torre。 “在嘈杂的量子计算机上识别受对称保护的拓扑状态”。 物理。 牧师莱特。 125、120502(2020 年)。
https:/ / doi.org/ 10.1103 / PhysRevLett.125.120502
被引用
[1] 马若晨和王冲,“平均对称保护拓扑相”, 的arXiv:2209.02723.
[2] Ivan Bardet、Ángela Capel、Li Gao、Angelo Lucia、David Pérez-García 和 Cambyse Rouzé,“自旋链通勤哈密顿量的快速热化”, 的arXiv:2112.00593.
以上引用来自 SAO / NASA广告 (最近成功更新为2022-11-12 04:01:10)。 该列表可能不完整,因为并非所有发布者都提供合适且完整的引用数据。
On Crossref的引用服务 找不到有关引用作品的数据(上一次尝试2022-11-12 04:01:08)。
该论文发表在《量子》杂志上 国际知识共享署名署名4.0(CC BY 4.0) 执照。 版权归原始版权持有者所有,例如作者或其所在机构。