إثبات مفاجأة لعلوم الكمبيوتر يذهل علماء الرياضيات

يوم الأحد ، 5 فبراير ، تلقى أولوف سيسسك وتوماس بلوم رسالة بريد إلكتروني تحتوي على اختراق مذهل في أكبر مشكلة لم يتم حلها في مجالهم. أرسل زاندر كيلي ، وهو طالب دراسات عليا في جامعة إلينوي ، أوربانا شامبين ، سيسسك وبلوم ورقة كتبها مع راغو ميكا من جامعة كاليفورنيا ، لوس أنجلوس. كان كل من كيلي وميكا من علماء الكمبيوتر ، عالم فكري بعيدًا عن التوليفات المضافة التي يدرسها سيسسك وبلوم.

"ذهلت في ذهني. مثل ، انتظر ، هل فعلوا هذا حقًا؟ " قال سيسسك ، محاضر في جامعة ستوكهولم. قال كيلي وميكا ، من خارج مجال التوافقية ، إنهما وجدا حدًا جديدًا - وأقل بشكل كبير - لحجم مجموعة من الأعداد الصحيحة التي لا توجد فيها مسافات متساوية لثلاثة منها (مع استبعاد مجموعات مثل 3 و 8 و 13 أو 101 و 201 و 301).

حطم ادعاء كيلي وميكا الرقم القياسي السابق ، تم تحقيقه في عام 2020 بقلم سيسسك وبلوم ، وهو زميل باحث في جامعة أكسفورد. قال بن غرين ، زميل بلومز في أكسفورد: "عمل بلوم وسيساك - عمل قوي جدًا - لقد أعطى حقًا انطباعًا بأنه من الصعب جدًا تحسينه". "بدا عالقًا جدًا في المكان الذي كان فيه."

على الرغم من أن كل من Bloom و Sisask كان لديهما أمور ملحة أخرى يجب أن يحضرها في الوقت الذي تلقوا فيه البريد الإلكتروني - فقد تبنى بلوم جروًا ، بينما كان سيسسك في منتصف الحركة - سرعان ما شرعوا في التحقق من الورقة الجديدة.

في غضون أيام ، اقتنع بلوم وسيساك بأن الدليل الجديد كان صحيحًا. وصفها سيسسك بأنها "أكبر نتيجة في المنطقة منذ 20 عامًا." حرصوا على أن يقدر الآخرون أفكار كيلي وميكا ، صاغوا تقرير شرح البرهان بمصطلحات مألوفة أكثر لعلماء الرياضيات.

قال ميكا إن استجابة المجتمع كانت "أكثر إيجابية مما كنت أعتقد. إنه لأمر مدهش أن ترى كل التعليقات ".

تقدم مطول

تسمى تسلسلات الأرقام المتباعدة بشكل متساوٍ التي سعى كيلي وميكا لتجنبها بالتعاقب الحسابي. يمكن أن تستمر إلى الأبد أو تحتوي فقط على بعض المصطلحات. ركز Kelley و Meka على التقدم المكون من ثلاثة أرقام فقط ، بعد سلسلة من الأبحاث التي غالبًا ما يتم تتبعها إلى ورقة 1936 بقلم بول إردوس وبول توران.

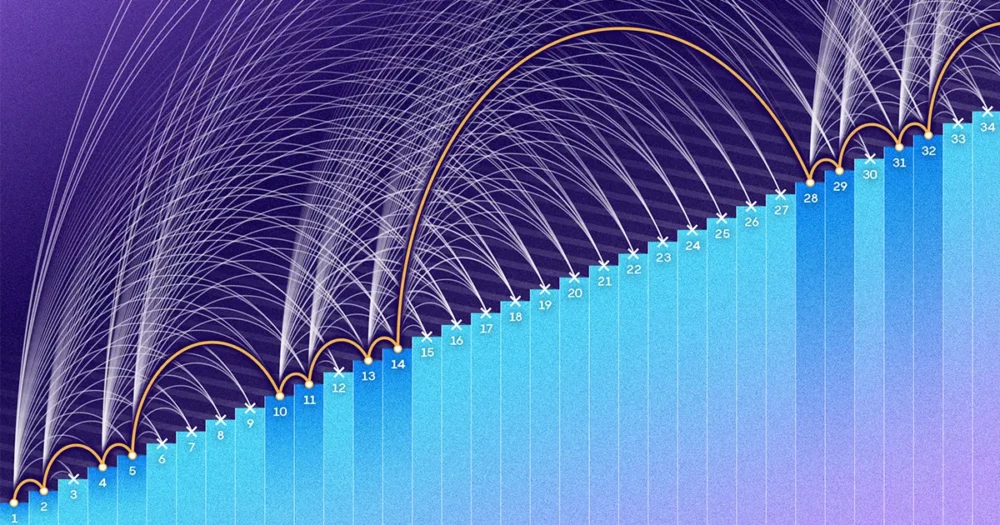
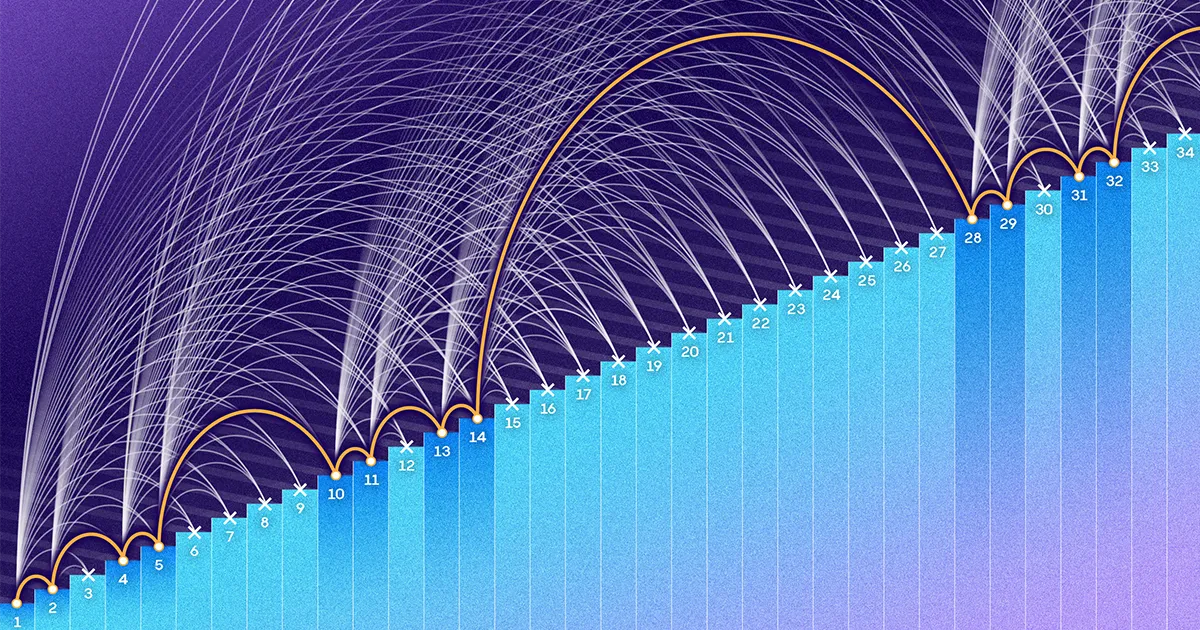
أراد Erdős و Turán معرفة عدد الأرقام الأصغر من بعض السقف N يمكن وضعها في مجموعة دون إنشاء أي تقدم حسابي من ثلاثة حدود. N قد يكون 1,000،1 أو XNUMX مليون أو عددًا ضخمًا لا يمكن تصوره. لقد توقعوا ذلك على أنه N نمت بشكل أكبر ، يجب أن تصبح المجموعة التي لا تحتوي على تعاقب لمدة ثلاثة فترات متناثرة بشكل لا يصدق. قد يكون إنشاء مثل هذه المجموعة بمثابة جمع الأحذية مع الإصرار على عدم وجود زوجين من نفس اللون. ربما يمكنك الاستمرار إلى الأبد ، ولكن مع زيادة حجم مجموعتك ، ستجد نفسك تضيف إليها بمعدل أبطأ وأبطأ.

أوضح ميكا: "هناك بعض الهياكل التي ستظهر في المجموعة ، بغض النظر عن كيفية اختيارك للمجموعة". "ما حجم المجموعة التي تحتاجها حقًا لضمان وجود هذا الهيكل هناك؟"

في عام 1946 ، فيليكس بيرند وجدت طريقة لبناء مجموعات من الأرقام بين 1 و N دون إنتاج أي تعاقب على ثلاث فترات. نتج عن طريقته مجموعات أكبر مثل N فعل ، ولكن ببطء مؤلم. متى N هو 100,000 ، تحتوي مجموعة Behrend على 171 عنصرًا فقط. متى N هو 1 مليون ، مجموعته بها 586 رقمًا - أقل من 0.06٪ من الأرقام بين 1 و 1 مليون.

أعطت مجموعات Behrend علماء الرياضيات أرضية للعمل معهم: يجب أن تكون أكبر مجموعة بدون تقدم ثلاثي الفترات على الأقل بحجم Behrend. في عام 1953 ، كلاوس روث قدمت سقف، إيجاد عتبة الماضي التي يجب أن تحتوي المجموعة حتمًا على تقدم ثلاثي المدى.

أثبت روث تخمين إردوس وتوران من خلال إظهار ذلك على أنه N تصبح أكبر ، المجموعة التي لا تحتوي على ثلاث فترات تعاقب ستشمل جزءًا أصغر دائمًا من الأرقام بين 1 و N. لكن سقف روث كان بعيدًا عن أرضية Behrend. أظهر بيرند أن 0.06٪ من العناصر بين 1 و 1 مليون يمكن أن تتناسب مع مجموعة خالية من التقدم. على الرغم من صعوبة حساب معادلة روث بدقة ، إلا أنها ليست قريبة من هذا المستوى المنخفض - فقد أشار أحد التقديرات التقريبية إلى أنها تحدد النسبة المئوية عند حوالي 40٪.

لكن الأمر الأكثر بروزًا من تلك الفجوة بالذات كان السلوك العام للصيغتين. ارسم كسر العناصر بين 1 و N التي تمثلها كل صيغة ، وسترى أن رقم بيرند يتقلص بسرعة إلى الصفر N ينمو. من ناحية أخرى ، ينزلق جزء روث نحو الصفر ، ولكن ببطء وبلطف. المنحنيان شكلان مختلفان تمامًا ، ويمكن أن تقع النسبة الحقيقية للعناصر الموجودة في مجموعة بدون تقدم حسابي ، على حد علم الرياضيات ، في أي مكان بينهما.

قال جرين بداية من الثمانينيات ، "كان هناك تسلسل طويل ، بعد فوات الأوان ، من التحسينات المتزايدة إلى حد ما من قبل عدد كبير من علماء الرياضيات المشهورين حقًا". بين الحين والآخر ، يقوم شخص ما بدفع الحد الأعلى لروث لأسفل بمقدار شعرة أو اثنتين ، وفي النهاية انخفض بشكل كبير. على النقيض من ذلك ، لم يتزحزح الحد الأدنى لبيرند لعقود. قال بلوم إن علماء الرياضيات بدأوا يعتقدون أن بيرند ربما لم يكن بعيدًا عن الإجابة الصحيحة.

حتى وصول ورقة Kelley and Meka في أوائل عام 2023 ، تم وضع الحد الأقصى لحجم المجموعة الخالية من التقدم من أسفل بواسطة صيغة Behrend ، ومن أعلى بواسطة Bloom و Sisask. لقد تجاوزت ورقة بلوم وسيساسك الصادرة في يوليو 2020 الحد "اللوغاريتمي" الحرج من خلال إظهار أن المجموعة الخالية من التقدم يجب أن تحتوي على أقل بكثير من N/(سجل N) عناصر. لكن نتيجتهم ما زالت أعلى من نتائج بيرند. الحد العلوي الجديد لكيلي وميكا أقرب بشكل كبير إلى الأرضية التي حددها Behrend.

قال تيرينس تاو ، عالم الرياضيات البارز في جامعة كاليفورنيا ، لوس أنجلوس: "لقد قفز Meka و Kelley نوعًا ما كل هذا التقدم التدريجي".

تكاد تكون صيغتها مماثلة لصيغة Behrend ، مع تعديل عدد قليل من المعلمات. مثل N تقترب من اللانهاية ، فإن قطعة من معادلة كيلي وميكا ستستقر في النهاية في منحنى يشبه منحنى بيرند. قال بلوم: "أي حد بهذا الشكل بدا وكأنه حلم مستحيل من قبل".

قال غرين: "لقد أصابني الذهول حقًا لأنهم أدخلوا مثل هذا التحسن".

تك مختلفة

 على الرغم من أن Kelley و Meka لم يجرما أبدًا المغامرة الكاملة في أبحاث الرياضيات البحتة من قبل ، إلا أن التقدم الحسابي كان مألوفًا لهما عندما بدآ. بشكل عام ، علماء الكمبيوتر "يتطلعون بجوع إلى الخارج لتقنيات من شأنها أن تعمل على حل مشاكلنا ،" قال كيلي. أصبحت الأدوات المستخدمة تاريخيًا لدراسة حجم مجموعة خالية من التقدم مستخدمة على نطاق واسع في حقل علوم الكمبيوتر الفرعي لنظرية التعقيد. إن مشكلة تضييق حجم مثل هذه المجموعة معروفة جيدًا لمنظري التعقيد باعتبارها مثالًا جوهريًا لتطبيق التقنيات التي تبحث في البنية الداخلية للمجموعات.

في أواخر عام 2021 ، كان كيلي وميكا يحللان فرص فوز فريق من اللاعبين في لعبة تعاونية معينة ، وهو نوع قياسي من مشاكل علوم الكمبيوتر. وخطر لهم أن التقنيات المستمدة من البحث حول حجم المجموعات الخالية من التقدم قد تكون مفيدة. لكنهم وجدوا أنه من الأسهل دراسة هذه التقنيات مباشرة بدلاً من تطبيقها على اللعبة التعاونية. قال كيلي: "كانت أفضل فكرة لدي حول كيفية إحراز تقدم في هذه المشكلة هي تحسين الأداة نفسها بالفعل ، وليس استخدامها بطريقة أكثر ذكاءً".

يتذكر ميكا "في مرحلة ما ، قررنا فقط العمل على هذه المسألة بشكل مباشر". بعد ستة أشهر ، توصل الباحثان إلى استراتيجيتهما واحتاجا فقط إلى تحديد كيفية تطبيق طريقتهما على المشكلة المطروحة.

لمعرفة كيف وصلوا إلى الحد الأعلى الجديد ، خذ أي مجموعة من الأرقام بين 1 و N. نسميها A. كثافة A هي النسبة المئوية للأرقام بين 1 و N التي يتضمنها. نظرًا لوجود الكثير من التدرجات الحسابية المحتملة بين 1 و N، إذا لم تختر عناصر A بعناية ، أي A مع كثافة عالية من المحتمل أن تحتوي على الكثير من التعاقب الحسابي.

في دليلهم ، تخيل كيلي وميكا ذلك A كان لديهم عدد قليل من التقدم الحسابي أو معدوم ، وحاولوا تتبع العواقب. لو A كانت كثيفة بدرجة كافية ، فقد أظهروا أن غياب التقدم استلزم مستوى من الهيكل الداخلي A هذا من شأنه أن يؤدي حتما إلى تناقض ، وهذا يعني ذلك A يجب ، بعد كل شيء ، أن تحتوي على تقدم واحد على الأقل.

لفهم هذا الهيكل ، اعتبروا المجموعة A + A، والتي تتكون من جميع الأرقام التي تم إجراؤها عن طريق إضافة عنصرين من A. لاحظوا ذلك إذا A يحتوي على عدد قليل نسبيًا من التقدم الحسابي ، وهذا يعني التكرار بين عناصر A + A: أزواج مختلفة من الأرقام من A غالبًا ما تضيف ما يصل إلى نفس الرقم.

يمكن تعريف الكثافة ليس فقط بالمقارنة مع جميع الأعداد الصحيحة بين 1 و N ولكن بالمقارنة مع بعض المجموعات الفرعية - قل فقط الأعداد الصحيحة الزوجية في تلك الفترة الزمنية ، أو فقط مضاعفات العدد 3. استخدم كيلي وميكا التكرار في A + A للعثور على مجموعة فرعية من الأعداد الصحيحة حيث عناصر A كانت شائعة بشكل خاص.

إذا احتوت A بشكل غير متناسب على العديد من مضاعفات الرقم 3 ، على سبيل المثال ، فإن Kelley و Meka سيركزان بعد ذلك على الجزء الذي يتضمن مضاعفات 3. فكرروا هذه الإستراتيجية مرارًا وتكرارًا. في كل مرة وجدوا مجموعات فرعية أصغر وأصغر من الأعداد الصحيحة ، فوقها Aستستمر كثافة الجراد في النمو والنمو. على سبيل المثال، A قد تحتوي على 10٪ من الأعداد الصحيحة بين 1 و N، و 15٪ من مضاعفات 3 في تلك الفترة ، و 25٪ من مضاعفات 3.

عندما يحدث شيء مثير للاهتمام A هو كبير. إذا تكرر الإجراء ، فإن كثافة A على بعض المجموعات الفرعية يتجاوز 100٪. هذا بالطبع مستحيل. A يمكن أن تحتوي ، على سبيل المثال ، على جميع مضاعفات العدد 24 ، لكنها لا يمكن أن تحتوي على أكثر من كل مضاعفات العدد. تنشأ هذه المفارقة فقط إذا A كبير بما يكفي لتبدأ به ، ولكن عندما يحدث ، فهذا يعني الافتراض بأن A لا يحتوي على أي تقدم حسابي لابد أنه كان خاطئًا.

إنها "حجة يربح فيها الجميع" متى A قال ميكا كبير. أيضاً A يتضمن الكثير من التدرجات الحسابية ، أو هناك الكثير من التكرار في A + A - في هذه الحالة يمكنهم استخدام إجراء اكتشاف المجموعة الفرعية (يسمى "استراتيجية زيادة الكثافة") لإظهار أن التقدم يجب أن يظهر في A. على الرغم من أن إستراتيجية زيادة الكثافة عبارة عن مخطط قديم في هذا المجال ، إلا أن كيلي وميكا نجحا في جعلها تعمل من أجل أصغر Aمن أي وقت مضى. مع ذلك ، كشفوا عن سقف جديد لحجم مجموعة خالية من التقدم.

بنى Kelley و Meka مزيجًا فريدًا من الأفكار من مخطط زيادة الكثافة. بدلاً من الخروج بإطار عمل جديد تمامًا ، أعادوا التفكير في الطريقة التي وجدوا بها مجموعتهم الفرعية الكثيفة. لهذا ، استخدموا تقنية أطلقوا عليها اسم "الغربلة" ، والتي تتكون من تبديل مجموعتهم بكمية ثابتة ، وتقاطعها مع نفسها ، وتكرار العملية عدة مرات. ما تبقى ، بعد عدة جولات من التقاطع ، هو مجموعة عالية التنظيم مع خصائص يمكن التنبؤ بها. على الرغم من استخدام الغربلة في أوراق أخرى ، إلا أنه لم يتم تجربتها مطلقًا في مشكلة التقدم على فترات الثلاثة.

النظر إلى الوراء

قام Kelley و Meka بسحب الحد الأقصى لحجم مجموعة خالية من التقدم بمقدار صادم عن طريق حقن أدوات مهملة مثل الغربلة في الأساليب التقليدية. قال بلوم: "لقد أظهر لنا كيلي وميكا أن هذه التقنيات ، التي كانت موجودة في العراء ، كانت أقوى بكثير مما كنا نتوقعه". وأضاف أنه في ضوء الفعالية المكتشفة حديثًا لهذه الأدوات ، "علينا أن نعود ونعيد النظر في كل شيء".

ظهرت استراتيجية زيادة الكثافة لأول مرة في ورقة روث منذ 70 عامًا ، وقد تم استخدامها في معظم الأوراق البحثية حول التقدم الحسابي منذ ذلك الحين. فوجئ جرين بإمكانية استخدام الإطار لإثبات حد منخفض مثل Kelley و Meka. قال: "اعتقدت أن هناك حاجة إلى شيء مختلف تمامًا وجذريًا".

كيلي متحمس لمواصلة غزوه في الرياضيات. قال: "ليس لدي نقص في الآمال والأحلام حول الكثير من المشاكل المختلفة التي سأعتبرها على الأقل مرتبطة روحيًا بهذا الأمر".

إن تمكن كيلي وميكا من اكتشاف قوة الأفكار التي تم التغاضي عنها من قبل يُظهر الطبيعة المتقطعة غالبًا للتقدم الرياضي - وهي صفة بالنسبة إلى تاو نعمة أكثر منها نقمة. قال: "ليس الأمر دائمًا هو أن الرياضيات تصبح أكثر صعوبة وأصعب وأصعب". "الحمد لله."