1Instituut-Lorentz, Universiteit Leiden, 2300 RA Leiden, Holland
2QuTech, Delft University of Technology, PO Box 5046, 2600 GA Delft, Holland og JARA Institute for Quantum Information, Forschungszentrum Juelich, D-52425 Juelich, Tyskland
3Google Quantum AI, 80636 München, Tyskland
Finder du denne artikel interessant eller vil du diskutere? Scite eller efterlade en kommentar på SciRate.
Abstrakt
Kvantefaseestimering er en hjørnesten i kvantealgoritmedesign, der giver mulighed for inferens af egenværdier af eksponentielt store sparsomme matricer. Den maksimale hastighed, hvormed disse egenværdier kan læres, -kendt som Heisenberg-grænsen-, er begrænset af grænser på kredsløbet kompleksitet, der kræves for at simulere en vilkårlig Hamiltonian. Enkeltkontrol-qubit-varianter af kvantefaseestimering, der ikke kræver sammenhæng mellem eksperimenter, har fået interesse i de seneste år på grund af lavere kredsløbsdybde og minimal qubit-overhead. I dette arbejde viser vi, at disse metoder kan opnå Heisenberg-grænsen, $also$, når man ikke er i stand til at forberede egentilstande af systemet. Givet en kvanteunderrutine, som giver eksempler på en `fasefunktion' $g(k)=sum_j A_j e^{i phi_j k}$ med ukendte egenfaser $phi_j$ og overlapper $A_j$ ved kvanteomkostninger $O(k)$, vi viser, hvordan man estimerer faserne ${phi_j}$ med (root-mean-square) fejl $delta$ for samlede kvanteomkostninger $T=O(delta^{-1})$. Vores skema kombinerer ideen om Heisenberg-begrænset flerordens kvantefaseestimering for en enkelt egenværdifase [Higgins et al (2009) og Kimmel et al (2015)] med subrutiner med såkaldt tæt kvantefaseestimering, som bruger klassisk behandling via tidsserieanalyse for QEEP-problemet [Somma (2019)] eller matrixblyantmetoden. For vores algoritme, som adaptivt retter valget for $k$ i $g(k)$, beviser vi Heisenberg-begrænset skalering, når vi bruger tidsserie/QEEP-underrutinen. Vi præsenterer numeriske beviser for, at ved hjælp af matrixblyantteknikken kan algoritmen også opnå Heisenberg-begrænset skalering.
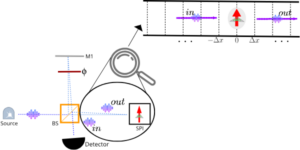
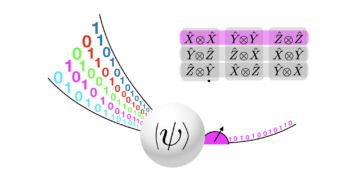
Udvalgt billede: Et Heisenberg-begrænset skema til at detektere flere faser $phi_j$. Først laves et indledende estimat af $phi_jin[0,2pi]$ fra en tidsserie ${langle Urangle, langle U^2rangle ldots}$. Derefter laves et estimat af $kphi_j$ for nogle $k>1$ ved at bruge ${langle U^{k}rangle, langle U^{2k}rangle,ldots }$. Dette genererer et mere nøjagtigt estimat på $phi_j$ (mindre fejlbjælker), men modulo $2pi/k$. Data fra den første estimering bruges til at stabilisere dette estimat og fjerne uønskede aliaser (stiplede linjer). Dette gentages for stadigt større værdier på $k$ for at nå Heisenberg-grænsen. Multiplikatoren $k$ er valgt baseret på de tidligere estimater for at muliggøre entydig estimering.
Populært resumé
► BibTeX-data
► Referencer
[1] BL Higgins, DW Berry, SD Bartlett, MW Mitchell, HM Wiseman og GJ Pryde. Demonstrerer Heisenberg-begrænset entydig faseestimering uden adaptive målinger. New J. Phys., 11 (7): 073023, 2009. 10.1088/1367-2630/11/7/073023. URL https:///arxiv.org/abs/0809.3308.
https://doi.org/10.1088/1367-2630/11/7/073023
arXiv: 0809.3308
[2] Shelby Kimmel, Guang Hao Low og Theodore J. Yoder. Robust kalibrering af et universelt single-qubit gate-sæt via robust faseestimering. Phys. Rev. A, 92: 062315, 2015. 10.1103/PhysRevA.92.062315. URL https:///arxiv.org/abs/1502.02677.
https:///doi.org/10.1103/PhysRevA.92.062315
arXiv: 1502.02677
[3] Rolando D. Somma. Kvanteegenværdiestimering via tidsserieanalyse. New J. Phys., 21: 123025, 2019. 10.1088/1367-2630/ab5c60. URL https://iopscience.iop.org/article/10.1088/1367-2630/ab5c60/pdf.
https://doi.org/10.1088/1367-2630/ab5c60
[4] Pawel Wocjan og Shengyu Zhang. Flere naturlige BQP-komplet problemer. ArXiv:quant-ph/0606179, 2006. 10.48550/arXiv.quant-ph/0606179. URL https:///arxiv.org/abs/quant-ph/0606179.
https:///doi.org/10.48550/arXiv.quant-ph/0606179
arXiv:quant-ph/0606179
[5] Peter W. Shor. Polynomial-tidsalgoritmer til primfaktorisering og diskrete logaritmer på en kvantecomputer. SIAM J. Sci. Stat. Comp., 26: 1484, 1997. 10.1137/S0097539795293172. URL https:///arxiv.org/abs/quant-ph/9508027.
https:///doi.org/10.1137/S0097539795293172
arXiv:quant-ph/9508027
[6] Aram W. Harrow, Avinatan Hassidim og Seth Lloyd. Kvantealgoritme til løsning af lineære ligningssystemer. Phys. Rev. Lett., 15 (103): 150502, 2009. 10.1103/PhysRevLett.103.150502. URL https:///arxiv.org/abs/0811.3171.
https:///doi.org/10.1103/PhysRevLett.103.150502
arXiv: 0811.3171
[7] James D. Whitfield, Jacob Biamonte og Alán Aspuru-Guzik. Simulering af elektronisk struktur Hamiltonians ved hjælp af kvantecomputere. Mol. Phys., 109: 735-750, 2011. 10.1080/00268976.2011.552441. URL https:///arxiv.org/abs/1001.3855.
https:///doi.org/10.1080/00268976.2011.552441
arXiv: 1001.3855
[8] MA Nielsen og IL Chuang. Kvanteberegning og kvanteinformation. Cambridge-serien om information og naturvidenskab. Cambridge University Press, 2000. ISBN 9780521635035. 10.1017/CBO9780511976667. URL https:///books.google.de/books?id=65FqEKQOfP8C.
https:///doi.org/10.1017/CBO9780511976667
https:///books.google.de/books?id=65FqEKQOfP8C
[9] R. Cleve, A. Ekert, C. Macchiavello og M. Mosca. Kvantealgoritmer revideret. Proceedings fra Royal Society of London. Serie A: Mathematical, Physical and Engineering Sciences, 454 (1969): 339–354, 1998. 10.1098/rspa.1998.0164. URL https://royalsocietypublishing.org/doi/abs/10.1098/rspa.1998.0164.
https:///doi.org/10.1098/rspa.1998.0164
[10] Vittorio Giovannetti, Seth Lloyd og Lorenzo Maccone. Kvantemetrologi. Physical review letters, 96 (1): 010401, 2006. 10.1103/PhysRevLett.96.010401. URL https:///journals.aps.org/prl/abstract/10.1103/PhysRevLett.96.010401.
https:///doi.org/10.1103/PhysRevLett.96.010401
[11] Wim van Dam, G. Mauro D'Ariano, Artur Ekert, Chiara Macchiavello og Michele Mosca. Optimale kvantekredsløb til generel faseestimering. Phys. Rev. Lett., 98: 090501, Mar 2007. 10.1103/PhysRevLett.98.090501. URL https://link.aps.org/doi/10.1103/PhysRevLett.98.090501.
https:///doi.org/10.1103/PhysRevLett.98.090501
[12] Dominic W Berry, Brendon L Higgins, Stephen D Bartlett, Morgan W Mitchell, Geoff J Pryde og Howard M Wiseman. Hvordan man udfører de mest nøjagtige mulige fasemålinger. Physical Review A, 80 (5): 052114, 2009. 10.1103/PhysRevA.80.052114.
https:///doi.org/10.1103/PhysRevA.80.052114
[13] Robert B. Griffiths og Chi-Sheng Niu. Semiklassisk Fourier-transformation til kvanteberegning. Physical Review Letters, 76 (17): 3228–3231, apr 1996. ISSN 1079-7114. 10.1103/physrevlett.76.3228. URL 10.1103/PhysRevLett.76.3228.
https:///doi.org/10.1103/physrevlett.76.3228
http:///10.1103/PhysRevLett.76.3228
[14] A. Yu. Kitaev. Kvantemålinger og det abelske stabilisatorproblem. ArXiv:quant-ph/9511026, 1995. 10.48550/arXiv.quant-ph/9511026. URL https:///arxiv.org/abs/quant-ph/9511026.
https:///doi.org/10.48550/arXiv.quant-ph/9511026
arXiv:quant-ph/9511026
[15] Dominic W. Berry, Graeme Ahokas, Richard Cleve og Barry C. Sanders. Effektive kvantealgoritmer til simulering af sparsomme Hamiltonianere. Comm. Matematik. Phys., 270 (359), 2007. 10.1007/s00220-006-0150-x. URL https:///arxiv.org/abs/quant-ph/0508139.
https:///doi.org/10.1007/s00220-006-0150-x
arXiv:quant-ph/0508139
[16] Nathan Wiebe og Chris Granade. Effektiv Bayesiansk fase estimering. Phys. Rev. Lett., 117: 010503, 2016. 10.1103/PhysRevLett.117.010503. URL https:///arxiv.org/abs/1508.00869.
https:///doi.org/10.1103/PhysRevLett.117.010503
arXiv: 1508.00869
[17] Krysta M. Svore, Matthew B. Hastings og Michael Freedman. Hurtigere fase estimering. Kvant. Inf. Comp., 14 (3-4): 306-328, 2013. 10.48550/arXiv.1304.0741. URL https:///arxiv.org/abs/1304.0741.
https:///doi.org/10.48550/arXiv.1304.0741
arXiv: 1304.0741
[18] Ewout van den Berg. Effektiv Bayesiansk faseestimering ved brug af blandede priors. ArXiv:2007.11629, 2020. 10.22331/q-2021-06-07-469. URL https:///arxiv.org/abs/2007.11629.
https://doi.org/10.22331/q-2021-06-07-469
arXiv: 2007.11629
[19] Thomas E O'Brien, Brian Tarasinski og Barbara M Terhal. Kvantefaseestimering af multiple egenværdier for småskala (støjende) eksperimenter. New J. Phys., 21: 023022, 2019. 10.1088/1367-2630/aafb8e. URL https://iopscience.iop.org/article/10.1088/1367-2630/aafb8e.
https://doi.org/10.1088/1367-2630/aafb8e
[20] David C. Rife og Robert R. Boorstyn. Enkelttoneparameterestimering fra tidsdiskrete observationer. IEEE Trans. Inf. Th., 20 (5): 591–598, 1974. 10.1109/TIT.1974.1055282. URL https://ieeexplore.ieee.org/document/1055282.
https:///doi.org/10.1109/TIT.1974.1055282
https:///ieeexplore.ieee.org/document/1055282
[21] Sirui Lu, Mari Carmen Bañuls og J. Ignacio Cirac. Algoritmer til kvantesimulering ved endelige energier. PRX Quantum, 2: 020321, 2020. 10.1103/PRXQuantum.2.020321. URL https:///journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.2.020321.
https:///doi.org/10.1103/PRXQuantum.2.020321
[22] TE O'Brien, S. Polla, NC Rubin, WJ Huggins, S. McArdle, S. Boixo, JR McClean og R. Babbush. Fejlafhjælpning via verificeret faseestimering. ArXiv:2010.02538, 2020. 10.1103/PRXQuantum.2.020317. URL https:///arxiv.org/abs/2010.02538.
https:///doi.org/10.1103/PRXQuantum.2.020317
arXiv: 2010.02538
[23] Alessandro Roggero. Spektral tæthedsestimering med den Gaussiske integraltransformation. ArXiv:2004.04889, 2020. 10.1103/PhysRevA.102.022409. URL https:///arxiv.org/abs/2004.04889.
https:///doi.org/10.1103/PhysRevA.102.022409
arXiv: 2004.04889
[24] András Gilyén, Yuan Su, Guang Hao Low og Nathan Wiebe. Kvantesingular værditransformation og videre: Eksponentielle forbedringer til kvantematrix-aritmetik. I Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, STOC 2019, side 193-204, New York, NY, USA, 2019. Association for Computing Machinery. ISBN 9781450367059. 10.1145/3313276.3316366. URL 10.1145/3313276.3316366.
https:///doi.org/10.1145/3313276.3316366
[25] O. Regev. En subeksponentiel tidsalgoritme for det dihedrale skjulte undergruppeproblem med polynomisk rum. ArXiv:quant-ph/0406151, 2004. 10.48550/arXiv.quant-ph/0406151. URL https:///arxiv.org/abs/quant-ph/0406151.
https:///doi.org/10.48550/arXiv.quant-ph/0406151
arXiv:quant-ph/0406151
[26] Lin Lin og Yu Tong. Heisenberg-begrænset jordtilstandsenergiestimering for tidlige fejltolerante kvantecomputere. ArXiv:2102.11340, 2021. 10.1103/PRXQuantum.3.010318. URL https:///arxiv.org/abs/2102.11340.
https:///doi.org/10.1103/PRXQuantum.3.010318
arXiv: 2102.11340
[27] Valentin Gebhart, Augusto Smerzi og Luca Pezzè. Heisenberg-begrænset bayesiansk multifase-estimeringsalgoritme. ArXiv:2010.09075, 2020. 10.1103/PhysRevApplied.16.014035. URL https:///arxiv.org/abs/2010.09075.
https:///doi.org/10.1103/PhysRevApplied.16.014035
arXiv: 2010.09075
[28] Andrew M. Childs, Yuan Su, Minh C. Tran, Nathan Wiebe og Shuchen Zhu. Teori om travfejl med kommutatorskalering. Phys. Rev. X, 11: 011020, februar 2021. 10.1103/PhysRevX.11.011020. URL https:///link.aps.org/doi/10.1103/PhysRevX.11.011020.
https:///doi.org/10.1103/PhysRevX.11.011020
[29] Harald Cramér. Matematiske metoder til statistik. Princeton University Press, 1946. ISBN 0691080046. 10.1515/9781400883868. URL https:///archive.org/details/in.ernet.dli.2015.223699.
https:///doi.org/10.1515/9781400883868
https:///archive.org/details/in.ernet.dli.2015.223699
[30] Calyampudi Radakrishna Rao. Information og den opnåelige nøjagtighed ved estimering af statistiske parametre. Tyr. Calcutta matematik. Soc., 37: 81-89, 1945. 10.1007/978-1-4612-0919-5_16. URL https:///link.springer.com/chapter/10.1007/978-1-4612-0919-5_16.
https://doi.org/10.1007/978-1-4612-0919-5_16
[31] Yingbo Hua og Tapan Sarkar. Matrix-blyantmetode til at estimere parametre for eksponentielt dæmpede/udæmpede sinusoider i støj. IEEE Transactions on Acoustic Speech and Signal Processing, 38 (5), 1990. 10.1109/29.56027. URL https://ieeexplore.ieee.org/document/56027.
https:///doi.org/10.1109/29.56027
https:///ieeexplore.ieee.org/document/56027
[32] Ankur Moitra. Superopløsning, ekstremalfunktioner og tilstandsnummeret for Vandermonde-matricer. I Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, STOC '15, side 821-830, New York, NY, USA, 2015. Association for Computing Machinery. ISBN 9781450335362. 10.1145/2746539.2746561. URL 10.1145/2746539.2746561.
https:///doi.org/10.1145/2746539.2746561
[33] Lin Lin og Yu Tong. Næsten optimal grundtilstandsforberedelse. Quantum, 4: 372, december 2020. ISSN 2521-327X. 10.22331/q-2020-12-14-372. Webadresse 10.22331/q-2020-12-14-372.
https://doi.org/10.22331/q-2020-12-14-372
Citeret af
[1] Casper Gyurik, Chris Cade og Vedran Dunjko, "Mod kvantefordel via topologisk dataanalyse", arXiv: 2005.02607.
[2] Kianna Wan, Mario Berta og Earl T. Campbell, "Randomized Quantum Algorithm for Statistical Phase Estimation", Physical Review Letters 129 3, 030503 (2022).
[3] Andrés Gómez og Javier Mas, "Hermitian matrix definiteness from quantum phase estimering", Kvanteinformationsbehandling 21 6, 213 (2022).
Ovenstående citater er fra SAO/NASA ADS (sidst opdateret 2022-10-07 02:35:12). Listen kan være ufuldstændig, da ikke alle udgivere leverer passende og fuldstændige citatdata.
Kunne ikke hente Crossref citeret af data under sidste forsøg 2022-10-07 02:35:10: Kunne ikke hente citerede data for 10.22331/q-2022-10-06-830 fra Crossref. Dette er normalt, hvis DOI blev registreret for nylig.
Dette papir er udgivet i Quantum under Creative Commons Attribution 4.0 International (CC BY 4.0) licens. Ophavsretten forbliver hos de originale copyright-indehavere, såsom forfatterne eller deres institutioner.