Dataloger tættere på det store algoritmiske mål | Quanta Magasinet

Hvis nogen beder dig om at afgøre, om to objekter er ens, kan det virke som en triviel anmodning. I de fleste hverdagssager er et hurtigt blik nok til, at du kan afgive en præcis bedømmelse.

Men i datalogi er det et langt mere involveret spørgsmål. Faktisk er det en, der skærer til det uafklarede hjerte af, hvad computere er i stand til. Afhængigt af hvad objekterne er, og hvordan du definerer ensartethed, ved vi stadig ikke, om computere kan besvare spørgsmålet hurtigt, eller om en langsom og besværlig tilgang i bund og grund er det bedste, de kan klare.

I løbet af det sidste årti har der været nogle vigtige resultater, der viser, at computere kan gøre det mindst en smule bedre end det. En af de største seneste resultater i datalogi var en hurtigere algoritme til at bestemme, hvornår to grafer er ens. 2015-værket, af László Babai fra University of Chicago, brød en vigtig beregningsmæssig hastighedsbarriere, men manglede en anden.

Nu et papir af Xiaorui Sun fra University of Illinois, Chicago har præsenteret en ny, hurtigere algoritme for et relateret spørgsmål kaldet gruppeisomorfismeproblemet, som handler om at vide, hvornår to matematiske objekter kaldet grupper er ens. Værket, lagt ud på nettet sidste marts, tager et lille skridt i retning af at afklare den underliggende beregningsmæssige kompleksitet, der er involveret i at sammenligne objekter.

Suns arbejde bryder en langvarig hastighedsgrænse for en bestemt klasse af grupper - den, der anses for at være den sværeste forekomst af gruppeisomorfiproblemet at løse. Hvis en algoritme hurtigt kan sammenligne grupper af denne slags, er håbet, at den hurtigt kan sammenligne grupper af enhver type.

"Vi kender ikke sådan et teorem, men vi har grund til at tro, at noget som det burde være sandt," sagde Josh Grochow fra University Colorado, Boulder.

Sammenligning af sammenligninger

For at afgøre, om to ting er ens på en præcis måde, skal du først definere "det samme." To rækker af tal kan betragtes som ens, hvis de kun indeholder de samme cifre, eller de skal muligvis have de samme cifre i samme rækkefølge.

Isomorfisme er en særlig form for ensartethed, der kommer meget op i matematik. Når to objekter er isomorfe for hinanden, betyder det groft sagt, at de indeholder de samme elementer, og at disse elementer er i samme forhold til hinanden.

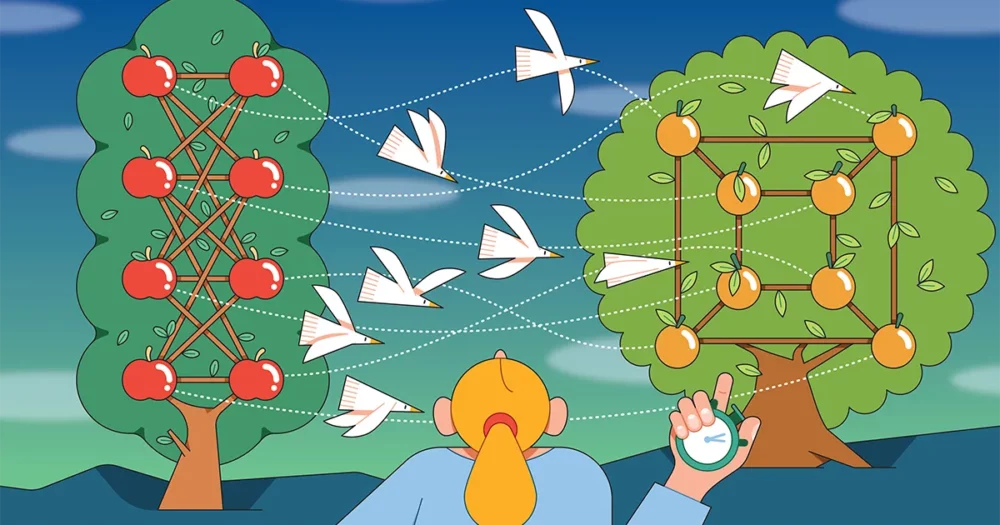
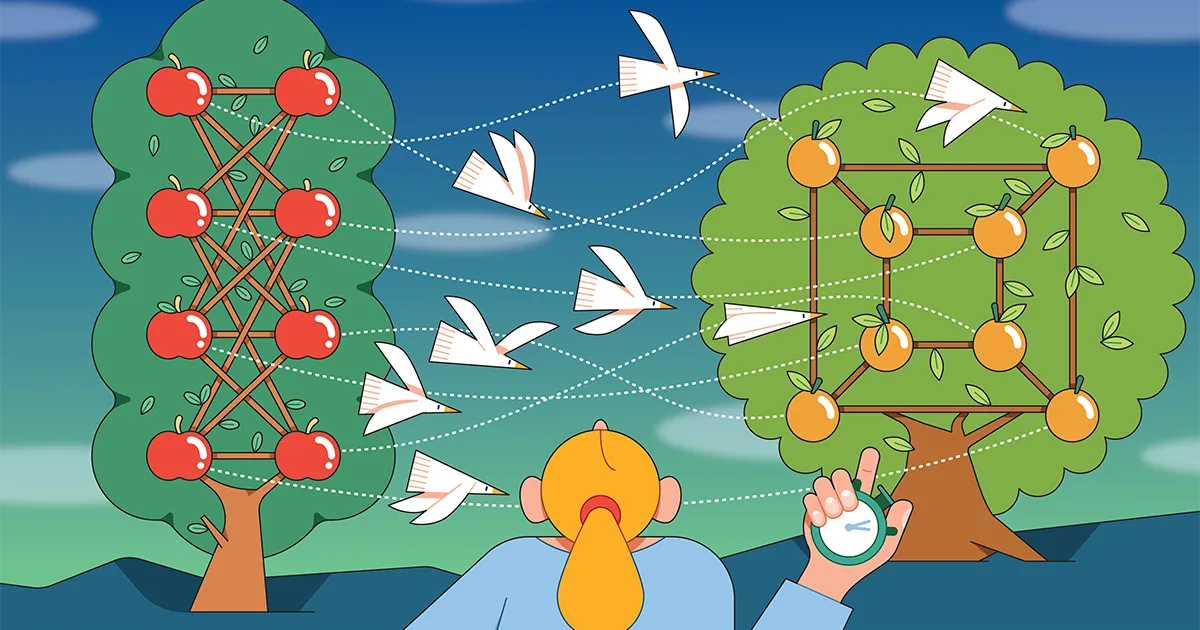
Grafer - samlinger af hjørner (prikker) forbundet med kanter (linjer) - giver en tilgængelig, visuel måde at se, hvordan isomorfi kan se ud. To grafer er isomorfe, hvis du kan matche knudepunkter i den ene graf med knudepunkter i den anden, således at spidser, der er forbundet med en kant i den første graf, er forbundet med en kant i den anden. Isomorfe grafer kan se anderledes ud på overfladen, men de deler en underliggende struktur.

Grupper er mere abstrakte end grafer, men de er stadig tilgængelige for sammenligning ved isomorfi. En gruppe er en samling af elementer - såsom tal - der kan kombineres med hinanden efter en eller anden operation, så resultatet også er i samlingen. For eksempel kan du have en gruppe, hvis elementer er heltal - alle positive og negative hele tal plus nul - og hvis operation er addition: Tilføj to vilkårlige heltal, og resultatet er altid et andet heltal.

To grupper er isomorfe, hvis du kan parre hvert element i den ene gruppe med et element i den anden, så resultatet af at operere på to elementer i den første gruppe er i overensstemmelse med resultatet af at operere på de ækvivalente værdier af disse elementer i den anden. gruppe.

Her er et simpelt eksempel på to grupper, hver med to elementer, der er isomorfe for hinanden. Den første gruppe består af tallene 0 og 1, og den anden gruppe består af bogstaverne a , b. Begge grupper indeholder en operation til at kombinere elementerne i gruppen på en bestemt måde, med resultaterne angivet i tabellerne nedenfor.

Grupperne er isomorfe, fordi 0 parrer med a, 1 par med b, og den strukturelle sammenhæng frembragt ved at kombinere elementer er den samme i begge grupper.

"Vi siger, at to grupper er isomorfe, hvis de grundlæggende er ækvivalente," sagde Sun.

Ubalanceret fremskridt

Isomorfisme er et vigtigt begreb i matematik - hvor grafer og grupper er udstrakte - fordi det giver matematikere mulighed for at se forbi overfladiske forskelle og fokusere på de måder, hvorpå relaterede objekter faktisk kan være de samme. Men det er også grundlæggende inden for datalogi; forskere leder ikke kun efter algoritmer, der bestemmer, om to objekter er isomorfe, men måler også, hvor hurtigt disse algoritmer kan køre.

Den måling kan være vanskelig. En algoritmes hastighed er baseret på, hvordan dens kørselstid ændres med størrelsen af ​​de objekter, den arbejder på. Forestil dig for eksempel, at du har to par grupper. I et par indeholder hver gruppe fem elementer. I den anden indeholder hver gruppe 10 elementer.

Du ville forvente, at det ville tage en algoritme længere tid at bestemme, om grupperne med flere elementer er isomorfe. Men hvor meget mere tid? Vil det tage dobbelt så lang tid? 5² længere? 2⁵ længere? Disse spørgsmål svarer til vigtige brede klassifikationer af algoritmisk hastighed: De kan køre i lineær tid (hvilket betyder i dette tilfælde, at det tager dobbelt så lang tid), polynomiel tid (5² længere) og eksponentiel tid (2⁵ længere).

Dataloger ved, hvilken hastighedskategori de fleste computerspørgsmål falder ind under, men ikke alle.

"De fleste er enten de nemmeste eller de sværeste [spørgsmål], men der er stadig flere undtagelser, som er ukendte," sagde Sun. Graf- og gruppeisomorfi er blandt disse undtagelser, hvilket er det, der gør dem så attraktive at studere.

I 1970s, Robert Tarjan fra Princeton University indså, at der er en algoritme, der kan bestemme, om to grupper er isomorfe med en kørselstid på $latex n^{{(log,n)}}$, hvor n er antallet af elementer i hver gruppe. Dette kaldes en kvasi-polynomial-tidsalgoritme, og i hierarkiet af runtimes er det bedre end eksponentiel tid (2ⁿ) men værre end polynomiel tid (n²). Dette er omtrent den samme hastighed som Babais grafisomorfialgoritme, og det er stadig det bedste, vi kan gøre for grupper næsten 50 år senere.

"Det betyder nogenlunde, at der ikke har været fremskridt i et halvt århundrede," sagde Sun.

På tidspunktet for Tarjans resultat blev gruppeisomorfiproblemet mere udbredt undersøgt end grafversionen. Det er vendt i dag, til dels fordi grafisomorfi har ansporet spændende innovationer, mens gruppeisomorfi er gået i stå.

"Alle vores værktøjer har været virkelig langsomme i årevis, og det har været svært at udnytte det, vi ved om algebraen [af grupper]," sagde James Wilson fra Colorado State University.

Men på trods af denne ulighed i udviklingen, har de to problemer en dybere sammenhæng end ligheden mellem deres navne: Gruppeisomorfiproblemet (i hvert fald i denne formulering) reduceres til grafisomorfiproblemet. Det betyder, at enhver algoritme, der kan løse grafproblemet, også kan løse gruppeproblemet på tilsvarende tid. Det omvendte er ikke sandt - fremskridt på gruppe betyder ikke fremskridt på grafen. Men manglen på fremskridt i gruppeproblemet har tynget matematikere, der søger tilsvarende gevinster på grafproblemet. Hvordan kan du opnå en sværere ting, hvis du ikke først kan opnå noget, der er tæt forbundet og virker endnu nemmere?

"Med andre ord," sagde Sun, "for yderligere at forbedre grafisomorfi er gruppeisomorfi en stor flaskehals."

Et Forvandlet Problem

Når fremskridt på et problem går i stå så længe, ​​som det gjorde for gruppeisomorfi, er opfindelsen normalt nødvendig for at blive løs. "Når du har et stort fremskridt, burde det være en indikation af, at der er en ny idé," sagde Grochow.

Suns arbejde indeholder et par ideer, der involverer at målrette mod en vigtig type gruppe og finde en smart måde at dele disse grupper op i stykker for at sammenligne dem.

De grupper, Suns algoritme virker for, kaldes p-grupper af klasse 2 og eksponent p. De ligner grupper, hvor produktet af to elementer er et andet element, og produktet forbliver det samme uanset i hvilken rækkefølge du gange dem. Men det, der virkelig betyder noget, er, hvad de repræsenterer for det overordnede gruppeisomorfiproblem. Disse grupper har en meget enkel struktur, hvilket betyder, at de skal være nemme at sammenligne. Men på trods af denne enkelhed havde forskerne ikke fundet ud af en måde at fremskynde algoritmen på. Indtil de kunne, føltes det håbløst at lave forbedringer til det generelle spørgsmål om gruppeisomorfi.

Sun begyndte med at skifte indstillingen fra grupper til matricer, arrays af tal, der tjener som grundlæggende objekter i lineær algebra. Dette var muligt på grund af en sætning fra 1930'erne kaldet Baer-korrespondancen, som forvandler denne version af gruppeisomorfismespørgsmålet til et fuldstændig analogt problem om matricer. Især arbejdede Sun med matrixrum, som er samlinger af matricer med en speciel egenskab: Den (lineære) kombination af vilkårlige to matricer i rummet er lig med en anden matrix i rummet.

Disse rum er med andre ord struktureret meget som grupper. Så i stedet for at prøve at forstå, hvornår to grupper er isomorfe, kunne Sun bare prøve at forstå, hvornår to matrixrum er isometriske - en forestilling om isomorfi af matrixrum, der svarer til gruppernes.

Sun var ikke den første forsker, der tog denne tilgang, men han var den første, der introducerede et yderligere trin: at opdele et matrixrum i to stykker. Et stykke er kernen i rummet, hvor alle matricerne er enkle. Det andet stykke er rummet omkring den kerne, hvor alle matricerne er særligt komplekse. Dette træk svarer til at opdele en gruppe i undergrupper, der kun indeholder nogle af de samlede elementer.

Sun anvendte derefter forskellige algoritmiske metoder til hver af disse stykker. Kernen har en enkel struktur, så han brugte en karakterisering af strukturen til at repræsentere den på en mere organiseret måde. Det ydre lag er mere komplekst, så der er ingen åbenlyst hurtig måde at sammenligne det med et andet lag. I stedet tager Suns metode en tilgang kaldet individualisering og forfining for at udelukke de fleste af de mulige måder at kortlægge et ydre lag på det andet og bruger derefter en computer til at gennemarbejde alle resterende mulige måder at afgøre, om der eksisterer en isomorf matchning.

Metoden ligner i sin ånd, hvordan du kan løse et sudoku-puslespil. Der er nogle firkanter, hvis potentielle værdier er begrænset af, hvad du allerede kender (kernen af ​​matrixrummet), hvilket giver dig mulighed for hurtigt at udfylde dem. Så er der andre (det ydre lag), som har færre begrænsninger, men som du kan finde ud af blot ved at prøve alle mulige værdier — og så længe der ikke er for mange af den slags firkanter, kan du stadig løse puslespillet i en rimelig tid.

"Jeg udfylder alle de ting, jeg hurtigt kan se er begrænsende, og nu går jeg måske tilbage og prøver mit hjerte på de manglende kasser," sagde Wilson. "Hvis du har indsnævret omfanget, er det nu et godt tidspunkt at skifte gear og bruge computeren til at søge efter de rigtige værdier."

Suns gennembrud viste, at det altid er muligt at foretage denne opdeling for de matrixrum svarende til p-grupper af klasse 2 og eksponent p. Han beviste derefter, at efter en sådan opdeling gør en kombination af algoritmiske teknikker det muligt at bestemme, om to rum er isomorfe i $latex n^{{(log,n)}^{5/6}}$ tid, en værdi, der er lidt lavere end Tarjans $latex n^{{(log,n)}}$ metode. (Begge algoritmer inkluderer også konstante termer, som ikke har den store effekt på kørselstiden, og som vi har udeladt for klarhedens skyld.)

Resultatet afgør ikke, hvilken hastighedskategori gruppe isomorfisme falder ind under; det er stadig et sted mellem eksponentiel og polynomiel tid. Men Sun har skubbet det lidt tættere på den polynomiske side af tingene, og der er grund til at tro, at mere end det burde være muligt. Når alt kommer til alt, giver hans arbejde dataloger en hurtigere gruppeisomorfi-algoritme til den hårdeste slags grupper, hvilket øger muligheden for, at en lignende speedup kan være inden for rækkevidde for grupper af enhver art.

"Hvis du kan løse det for p-grupper, nok kan I løse det hele," sagde Grochow. "Måske."