Minimale Trotterisierungsformeln für einen zeitabhängigen Hamilton-Operator

Neuauflage von Plato

Verfolger: 0

Tatsuhiko N. Ikeda^1,2,3, Asir Abrar⁴, Isaac L. Chuang⁵, und Sho Sugiura^4,6

¹RIKEN Center for Quantum Computing, Wako, Saitama 351-0198, Japan
²Fachbereich Physik, Boston University, Boston, Massachusetts 02215, USA
³Institut für Festkörperphysik, Universität Tokio, Kashiwa, Chiba 277-8581, Japan
⁴Labor für Physik und Informatik, NTT Research, Inc., 940 Stewart Dr., Sunnyvale, Kalifornien, 94085, USA
⁵Fakultät für Physik, Fakultät für Elektrotechnik und Informatik und Co-Design Center for Quantum Advantage, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
⁶Labor für Nuklearwissenschaft, Massachusetts Institute of Technology, Cambridge, 02139, MA, USA

Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.

Abstrakt

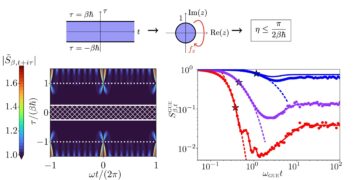
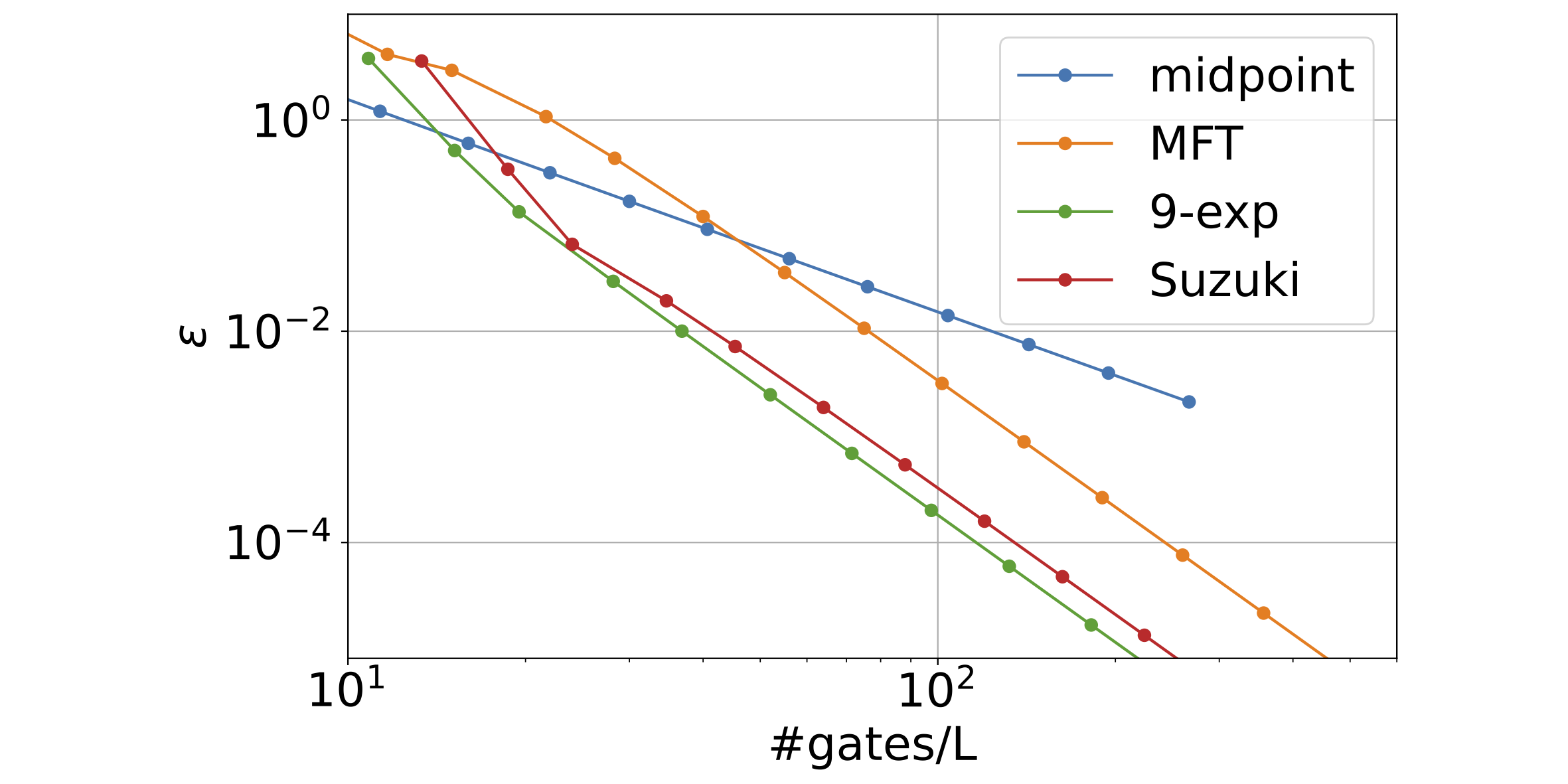
Wenn ein Zeitpropagator $e^{delta t A}$ für die Dauer $delta t$ aus zwei nicht kommutierenden Teilen $A=X+Y$ besteht, zerlegt die Trotterisierung den Propagator ungefähr in ein Produkt von Exponentialfunktionen von $X$ und $Y$ . In Quantencomputern und klassischen Computern wurden verschiedene Trotterisierungsformeln verwendet, für die Trotterisierung mit dem zeitabhängigen Generator $A(t)$ ist jedoch viel weniger bekannt. Hier entwickeln wir für $A(t)$, das durch die Summe zweier Operatoren $X$ und $Y$ mit zeitabhängigen Koeffizienten $A(t) = x(t) X + y(t) Y$ gegeben ist, a systematischer Ansatz zur Ableitung von Trotterisierungsformeln höherer Ordnung mit minimal möglichen Exponentialfunktionen. Insbesondere erhalten wir Trotterisierungsformeln vierter und sechster Ordnung mit sieben bzw. fünfzehn Exponentialfunktionen, die nicht größer sind als die für zeitunabhängige Generatoren. Wir konstruieren auch eine weitere Formel vierter Ordnung, die aus neun Exponentialfunktionen mit einem kleineren Fehlerkoeffizienten besteht. Abschließend vergleichen wir die Formeln vierter Ordnung in einer Hamilton-Simulation für eine Quanten-Ising-Kette numerisch und zeigen, dass die 9-Exponentialformel kleinere Fehler pro lokalem Quantengatter mit sich bringt als die bekannte Suzuki-Formel.

Minimale Trotterisierungsformeln für eine zeitabhängige Hamilton-Funktion von PlatoBlockchain Data Intelligence. Vertikale Suche. Ai.

► BibTeX-Daten

@article{Ikeda2023minimum, doi = {10.22331/q-2023-11-06-1168}, url = {https://doi.org/10.22331/q-2023-11-06-1168}, title = {Minimum { T}Rotterisierungs-{F}ormulen für einen {Zeit-{D}abhängigen {H}amiltonian}, Autor = {Ikeda, Tatsuhiko N. und Abrar, Asir und Chuang, Isaac L. und Sugiura, Sho}, Zeitschrift = {{Quantum}}, issn = {2521-327X}, verleger = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, Band = {7}, Seiten = {1168}, Monat = November, Jahr = {2023} }

► Referenzen

[1] Dong An, Di Fang und Lin Lin. Zeitabhängige unbeschränkte Hamilton-Simulation mit Vektornormskalierung. Quantum, 5: 459, 2021. https:///doi.org/10.22331/q-2021-05-26-459.
https://doi.org/10.22331/q-2021-05-26-459

[2] S. Blanes und P.C. Jammern. Praktische symplektische partitionierte Runge-Kutta- und Runge-Kutta-Nyström-Methoden. Journal of Computational and Applied Mathematics, 142 (2): 313–330, 2002. https://doi.org/10.1016/S0377-0427(01)00492-7.
https://doi.org/10.1016/S0377-0427(01)00492-7

[3] S. Blanes, F. Casas, J.A. Oteo und J. Ros. Die Magnus-Erweiterung und einige ihrer Anwendungen. Physics Reports, 470 (5): 151–238, 2009. https:///doi.org/10.1016/j.physrep.2008.11.001.
https://doi.org/ 10.1016/j.physrep.2008.11.001

[4] Sergey Bravyi, David P. DiVincenzo und Daniel Loss. Schrieffer-Wolff-Transformation für Quanten-Vielteilchensysteme. Annals of Physics, 326 (10): 2793–2826, 2011. https:///doi.org/10.1016/j.aop.2011.06.004.
https: / / doi.org/ 10.1016 / j.aop.2011.06.004

[5] Andrew M. Childs, Yuan Su, Minh C. Tran, Nathan Wiebe und Shuchen Zhu. Theorie des Traberfehlers mit Kommutatorskalierung. Physik. Rev. X, 11: 011020, 2021. https://doi.org/10.1103/PhysRevX.11.011020.
https://doi.org/ 10.1103/PhysRevX.11.011020

[6] Etienne Forest und Ronald D. Ruth. Symplektische Integration vierter Ordnung. Physica D: Nonlinear Phenomena, 43 (1): 105–117, 1990. https:///doi.org/10.1016/0167-2789(90)90019-L.
https://doi.org/10.1016/0167-2789(90)90019-L

[7] Naomichi Hatano und Masuo Suzuki. Exponentielle Produktformeln höherer Ordnung finden, Seiten 37–68. Springer Berlin Heidelberg, Berlin, Heidelberg, 2005. ISBN 978-3-540-31515-5. https:///doi.org/10.1007/11526216_2.
https: / / doi.org/ 10.1007 / 11526216_2

[8] J. Huyghebaert und H. De Raedt. Produktformelmethoden für zeitabhängige Schrödinger-Probleme. Journal of Physics A: Mathematical and General, 23 (24): 5777, 1990. https:///doi.org/10.1088/0305-4470/23/24/019.
https://doi.org/10.1088/0305-4470/23/24/019

[9] Tatsuhiko N. Ikeda und Keisuke Fujii. Trotter24: Eine präzisionsgarantierte adaptive Stepsize-Traberisierung für Hamilton-Simulationen. arXiv:2307.05406, 2023. https:///doi.org/10.48550/arXiv.2307.05406.
https:///doi.org/10.48550/arXiv.2307.05406
arXiv: 2307.05406

[10] A Iserles, A Marthinsen und S P Nørsett. Zur Implementierung der Methode der Magnusreihen für lineare Differentialgleichungen. BIT Numerical Mathematics, 39 (2): 281–304, 1999. https://doi.org/10.1023/A:1022393913721.
https: / / doi.org/ 10.1023 / A: 1022393913721

[11] Tobias Jahnke und Christian Lubich. Fehlergrenzen für exponentielle Operatoraufteilungen. BIT Numerical Mathematics, 40 (4): 735–744, 2000. https://doi.org/10.1023/A:1022396519656.
https: / / doi.org/ 10.1023 / A: 1022396519656

[12] Tosio Kato. Zur Trotter-Lie-Produktformel. Proceedings of the Japan Academy, 50 (9): 694–698, 1974. https:///doi.org/10.3792/pja/1195518790.
https:///doi.org/10.3792/pja/1195518790

[13] Guang Hao Low und Isaac L. Chuang. Optimale Hamilton-Simulation durch Quantensignalverarbeitung. Physik. Rev. Lett., 118: 010501, 2017. https:///doi.org/10.1103/PhysRevLett.118.010501.
https://doi.org/ 10.1103/PhysRevLett.118.010501

[14] Guang Hao Low und Nathan Wiebe. Hamilton-Simulation im Interaktionsbild. arXiv:1805.00675, 2018. https:///doi.org/10.48550/arXiv.1805.00675.
https:///doi.org/10.48550/arXiv.1805.00675
arXiv: 1805.00675

[15] John M. Martyn, Zane M. Rossi, Andrew K. Tan und Isaac L. Chuang. Große Vereinheitlichung der Quantenalgorithmen. PRX Quantum, 2: 040203, 2021. https:///doi.org/10.1103/PRXQuantum.2.040203.
https: / / doi.org/ 10.1103 / PRXQuantum.2.040203

[16] Kaoru Mizuta und Keisuke Fujii. Optimale Hamilton-Simulation für zeitperiodische Systeme. Quantum, 7: 962, 2023. https:///doi.org/10.22331/q-2023-03-28-962.
https://doi.org/10.22331/q-2023-03-28-962

[17] I P Omelyan, I M Mryglod und R Folk. Optimierte Forest-Ruth- und Suzuki-ähnliche Algorithmen zur Bewegungsintegration in Vielteilchensystemen. Computer Physics Communications, 146 (2): 188–202, 2002. https:///doi.org/10.1016/S0010-4655(02)00451-4.
https://doi.org/10.1016/S0010-4655(02)00451-4

[18] Johann Ostmeyer. Optimierte Trotter-Zerlegungen für klassisches und Quantencomputing. Journal of Physics A: Mathematical and Theoretical, 56 (28): 285303, 2023. https://doi.org/10.1088/1751-8121/acde7a.
https:///doi.org/10.1088/1751-8121/acde7a

[19] David Poulin, Angie Qarry, Rolando Somma und Frank Verstraete. Quantensimulation zeitabhängiger Hamiltonoperatoren und die praktische Illusion des Hilbert-Raums. Physik. Rev. Lett., 106: 170501, 2011. https:///doi.org/10.1103/PhysRevLett.106.170501.
https://doi.org/ 10.1103/PhysRevLett.106.170501

[20] J. R. Schrieffer und P. A. Wolff. Beziehung zwischen den Anderson- und Kondo-Hamiltonianern. Physik. Rev., 149: 491–492, 1966. https:///doi.org/10.1103/PhysRev.149.491.
https: / / doi.org/ 10.1103 / PhysRev.149.491

[21] Andrew T. Sornborger, Phillip Stancil und Michael R. Geller. Auf dem Weg zur vorschwelligen Gate-basierten Quantensimulation der chemischen Dynamik: Verwendung potenzieller Energieoberflächen zur Simulation von molekularen Kollisionen mit wenigen Kanälen. Quantum Information Processing, 17 (5): 106, 2018. https:///doi.org/10.1007/s11128-018-1878-x.
https: / / doi.org/ 10.1007 / s11128-018-1878-x

[22] Masuo Suzuki. Fraktale Zerlegung exponentieller Operatoren mit Anwendungen auf Vielteilchentheorien und Monte-Carlo-Simulationen. Physics Letters A, 146 (6): 319–323, 1990. https:///doi.org/10.1016/0375-9601(90)90962-N.
https://doi.org/10.1016/0375-9601(90)90962-N

[23] Masuo Suzuki. Allgemeine Zerlegungstheorie geordneter Exponentialfunktionen. Proceedings of the Japan Academy, Series B, 69 (7): 161–166, 1993. https:///doi.org/10.2183/pjab.69.161.
https: / / doi.org/ 10.2183 / pjab.69.161

[24] H. F. Trotter. Über das Produkt von Halbgruppen von Operatoren. Proceedings of the American Mathematical Society, 10 (4): 545–551, 1959. https://doi.org/10.2307/2033649.
https: / / doi.org/ 10.2307 / 2033649

[25] Jacob Watkins, Nathan Wiebe, Alessandro Roggero und Dean Lee. Zeitabhängige Hamilton-Simulation unter Verwendung diskreter Uhrenkonstruktionen. arXiv:2203.11353, 2022. https:///doi.org/10.48550/arXiv.2203.11353.
https:///doi.org/10.48550/arXiv.2203.11353
arXiv: 2203.11353

[26] Nathan Wiebe, Dominic Berry, Peter Høyer und Barry C. Sanders. Zerlegungen höherer Ordnung geordneter Operator-Exponentialfunktionen. Journal of Physics A: Mathematical and Theoretical, 43 (6): 065203, Januar 2010. https://doi.org/10.1088/1751-8113/43/6/065203.
https://doi.org/10.1088/1751-8113/43/6/065203

[27] Haruo Yoshida. Konstruktion symplektischer Integratoren höherer Ordnung. Physics Letters A, 150 (5): 262–268, 1990. https:///doi.org/10.1016/0375-9601(90)90092-3.
https://doi.org/10.1016/0375-9601(90)90092-3

[28] Hongzheng Zhao, Marin Bukov, Markus Heyl und Roderich Moessner. Anpassung der Trabbewegung und Energieselbstkorrektur für Nisq-Geräte und darüber hinaus. PRX Quantum, 4: 030319, 2023a. https:///doi.org/10.1103/PRXQuantum.4.030319.
https: / / doi.org/ 10.1103 / PRXQuantum.4.030319

[29] Hongzheng Zhao, Marin Bukov, Markus Heyl und Roderich Moessner. Adaptive Trotterisierung für zeitabhängige hamiltonsche Quantendynamik unter Verwendung momentaner Erhaltungssätze. arXiv:2307.10327, 2023b. https:///doi.org/10.48550/arXiv.2307.10327.
https:///doi.org/10.48550/arXiv.2307.10327
arXiv: 2307.10327

Zitiert von

[1] Hongzheng Zhao, Marin Bukov, Markus Heyl und Roderich Moessner, „Adaptive Trotterisierung für zeitabhängige Hamilton-Quantendynamik unter Verwendung momentaner Erhaltungsgesetze“, arXiv: 2307.10327, (2023).

[2] Tatsuhiko N. Ikeda und Keisuke Fujii, „Trotter24: Eine präzisionsgarantierte adaptive Stufengrößen-Trotterisierung für Hamilton-Simulationen“, arXiv: 2307.05406, (2023).

[3] Pooja Siwach, Kaytlin Harrison und A. Baha Balantekin, „Kollektive Neutrino-Oszillationen auf einem Quantencomputer mit hybridem quantenklassischem Algorithmus“, Physische Überprüfung D 108 8, 083039 (2023).

Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2023, 11:06:13 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.

Konnte nicht abrufen Crossref zitiert von Daten während des letzten Versuchs 2023-11-06 13:45:46: Von Crossref konnten keine zitierten Daten für 10.22331 / q-2023-11-06-1168 abgerufen werden. Dies ist normal, wenn der DOI kürzlich registriert wurde.

Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.

SEO-gestützte Content- und PR-Distribution. Holen Sie sich noch heute Verstärkung.
PlatoData.Network Vertikale generative KI. Motiviere dich selbst. Hier zugreifen.
PlatoAiStream. Web3-Intelligenz. Wissen verstärkt. Hier zugreifen.
PlatoESG. Kohlenstoff, CleanTech, Energie, Umwelt, Solar, Abfallwirtschaft. Hier zugreifen.
PlatoHealth. Informationen zu Biotechnologie und klinischen Studien. Hier zugreifen.
Quelle: https://quantum-journal.org/papers/q-2023-11-06-1168/

Zeitstempel: 6. November 2023

Zeitstempel: 23. Mai 2023

Minimale Trotterisierungsformeln für einen zeitabhängigen Hamilton-Operator

Neuauflage von Plato

Abstrakt

► BibTeX-Daten

► Referenzen

Zitiert von

Mehr von Quantenjournal

Der minimale Kommunikationsaufwand für die Simulation verschränkter Qubits

Quantum Liouvillian außergewöhnliche und teuflische Punkte für bosonische Felder mit quadratischen Hamiltonianern: Der Ansatz der Heisenberg-Langevin-Gleichung

Saisonaler Unterwerfungsschlaf

Völlig positive Karte für rauschgetriebene Quantensysteme, abgeleitet durch die Keldysh-Erweiterung

Analytische Einschränkungen begrenzten den Abfall des spektralen Formfaktors

Symmetriegeschützte topologische Ordnung in offenen Quantensystemen

Energiemessungen bleiben über die schwache Kopplung hinaus thermometrisch optimal

Zeitoptimale Multi-Qubit-Gates: Komplexität, effiziente Heuristik und Gate-Zeitgrenzen

Eine relativistische diskrete Raumzeitformulierung von 3+1 QED

Quantenvorteil durch hochdimensionale verdrehte Photonen als endliche Quantenautomaten

Exakte und effiziente Lanczos-Methode auf einem Quantencomputer

Über uns

Vertikale Suche & Ai

Plattform

Bleiben Sie in Verbindung

Konto