Verbesserte Genauigkeit für Trabersimulationen mithilfe der Tschebyscheff-Interpolation

Verbesserte Genauigkeit für Trabersimulationen mithilfe der Tschebyscheff-Interpolation

Zeitstempel: 26. Februar 2024, 9:34 Uhr

Gumaro Rendon1, Jacob Watkins2und Nathan Wiebe3,4

1Zapata Computing Inc., Boston, MA 02110, USA
2Einrichtung für seltene Isotopenstrahlen, Michigan State University, East Lansing, MI 48824, USA
3Institut für Informatik, University of Toronto, Toronto, ON M5S 2E4, Kanada
4Pacific Northwest National Laboratory, Richland, WA 99352, USA

Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.

Abstrakt

Die Quantenmetrologie ermöglicht die Messung der Eigenschaften eines Quantensystems am optimalen Heisenberg-Limit. Wenn jedoch die relevanten Quantenzustände mittels digitaler Hamilton-Simulation vorbereitet werden, führen die aufgelaufenen algorithmischen Fehler zu Abweichungen von dieser Grundgrenze. In dieser Arbeit zeigen wir, wie algorithmische Fehler aufgrund der trotterisierten Zeitentwicklung durch den Einsatz standardmäßiger Polynominterpolationstechniken gemindert werden können. Unser Ansatz besteht darin, auf eine Trotter-Schrittweite von Null zu extrapolieren, ähnlich den rauschfreien Extrapolationstechniken zur Minderung von Hardwarefehlern. Wir führen eine strenge Fehleranalyse des Interpolationsansatzes zur Schätzung von Eigenwerten und zeitlich entwickelten Erwartungswerten durch und zeigen, dass die Heisenberg-Grenze bis zu polylogarithmischen Faktoren im Fehler erreicht wird. Unsere Arbeit legt nahe, dass mit Trotter und klassischen Ressourcen allein für eine Reihe relevanter algorithmischer Aufgaben Genauigkeiten erreicht werden können, die denen moderner Simulationsalgorithmen nahe kommen.

Verbesserte Genauigkeit für Trabersimulationen mithilfe der Tschebyscheff-Interpolation PlatoBlockchain Data Intelligence. Vertikale Suche. Ai.

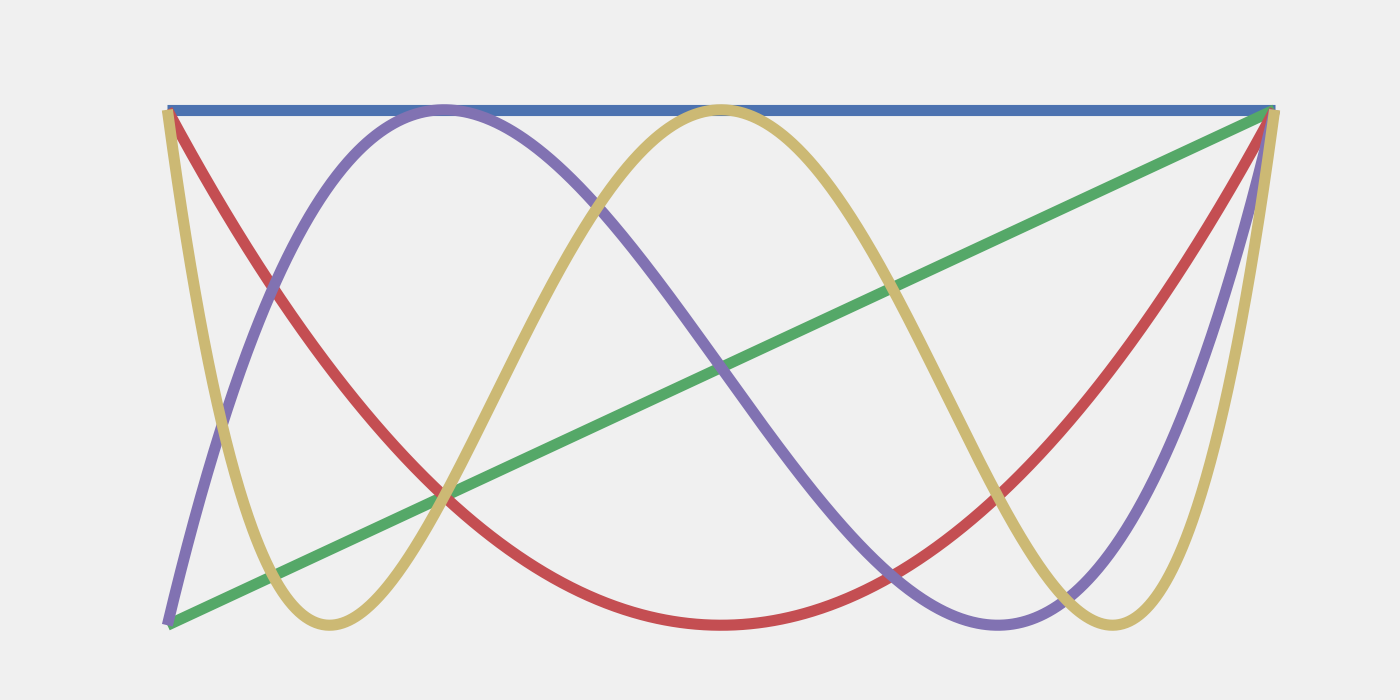
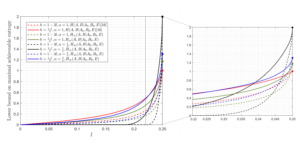
Ausgewähltes Bild: Die ersten fünf Tschebyscheff-Polynome. Die Interpolation an den Tschebyscheff-Nullstellen dient als robustes Schema zur Trotter-Fehlerminderung.

[Eingebetteten Inhalt]

Populäre Zusammenfassung

Quantencomputer haben das Potenzial, unser Verständnis von Chemie, Materialien, Kernphysik und anderen wissenschaftlichen Disziplinen durch verbesserte Quantensimulation zu verbessern. Für diese Aufgabe stehen mehrere Quantenalgorithmen zur Verfügung, von denen Trotter-Formeln aufgrund ihrer Einfachheit und geringen Vorlaufkosten häufig bevorzugt werden. Leider sind Trotter-Formeln im Vergleich zu ihren neueren und anspruchsvolleren Konkurrenten theoretisch relativ ungenau. Obwohl mehr Rechenzeit hilfreich sein kann, wird diese Strategie auf den heutigen rauschenden Quantengeräten schnell undurchführbar und die Fähigkeit, lange, ununterbrochene Berechnungen durchzuführen, ist begrenzt.

Um Fehler in Trotter-Simulationen zu verringern, ohne die Quantenverarbeitungszeit zu erhöhen, verwenden wir Polynome, um die Beziehung zwischen Fehler und Schrittgröße zu lernen. Indem wir Daten für verschiedene Schrittgrößen sammeln, können wir die Daten mit einem Polynom interpolieren, also verknüpfen, und dann das erwartete Verhalten für sehr kleine Schrittgrößen abschätzen. Wir beweisen mathematisch, dass unser Ansatz bei zwei grundlegenden Aufgaben zu asymptotischen Genauigkeitsverbesserungen gegenüber dem Standard-Trotter führt: der Schätzung von Eigenwerten und der Schätzung von Erwartungswerten.

Unsere Methode ist einfach und praktisch und erfordert nur Standardtechniken der Quanten- und klassischen Berechnung. Wir glauben, dass unsere Arbeit eine starke theoretische Grundlage für weitere Untersuchungen zur algorithmischen Fehlerminderung bietet. Erweiterungen dieser Arbeit könnten in verschiedene Richtungen erfolgen, von der Eliminierung künstlicher Annahmen in unserer Analyse bis hin zur Demonstration verbesserter Quantensimulationen.

► BibTeX-Daten

► Referenzen

[1] S. Lloyd, Universal Quantum Simulators, Science 273 (1996) 1073.
https: / / doi.org/ 10.1126 / science.273.5278.1073

[2] M. Reiher, N. Wiebe, KM Svore, D. Wecker und M. Troyer, Aufklärung von Reaktionsmechanismen auf Quantencomputern, Proceedings of the National Academy of Sciences 114 (2017) 7555.
https: / / doi.org/ 10.1073 / pnas.161915211

[3] JD Whitfield, J. Biamonte und A. Aspuru-Guzik, Simulation elektronischer Struktur-Hamiltonianer mithilfe von Quantencomputern, Molecular Physics 109 (2011) 735.
https: / / doi.org/ 10.1080 / 00268976.2011.552441

[4] J. Lee, DW Berry, C. Gidney, WJ Huggins, JR McClean, N. Wiebe et al., Noch effizientere Quantenberechnungen der Chemie durch Tensor-Hyperkontraktion, PRX Quantum 2 (2021) 030305.
https: / / doi.org/ 10.1103 / PRXQuantum.2.030305

[5] V. von Burg, GH Low, T. Häner, DS Steiger, M. Reiher, M. Roetteler et al., Quantum Computing Enhanced Computational Catalysis, Physical Review Research 3 (2021) 033055.
https: / / doi.org/ 10.1103 / PhysRevResearch.3.033055

[6] SP Jordan, KS Lee und J. Preskill, Quantenalgorithmen für Quantenfeldtheorien, Science 336 (2012) 1130.
https: / / doi.org/ 10.1126 / science.1217069

[7] AF Shaw, P. Lougovski, JR Stryker und N. Wiebe, Quantenalgorithmen zur Simulation des Gitterschwingermodells, Quantum 4 (2020) 306.
https:/​/​doi.org/​10.22331/​q-2020-08-10-306

[8] N. Klco, MJ Savage und JR Stryker, Su (2) nicht-abelsche Eichfeldtheorie in einer Dimension auf digitalen Quantencomputern, Physical Review D 101 (2020) 074512.
https://doi.org/ 10.1103/PhysRevD.101.074512

[9] AM Childs und N. Wiebe, Hamilton-Simulation unter Verwendung linearer Kombinationen einheitlicher Operationen, Quantum Info. Berechnen. 12 (2012) 901–924.
https: / / doi.org/ 10.26421 / QIC12.11-12-1

[10] GH Low, V. Kliuchnikov und N. Wiebe, Gut konditionierte Multiprodukt-Hamilton-Simulation, arXiv:1907.11679 (2019).
https://​/​doi.org/​10.48550/​arXiv.1907.11679
arXiv: 1907.11679

[11] DW Berry, AM Childs, R. Cleve, R. Kothari und RD Somma, Simulation der Hamilton-Dynamik mit einer verkürzten Taylor-Reihe, Physical Review Letters 114 (2015) 090502.
https://doi.org/ 10.1103/PhysRevLett.114.090502

[12] GH Low und N. Wiebe, Hamilton-Simulation im Interaktionsbild, arXiv:1805.00675 (2018).
https://​/​doi.org/​10.48550/​arXiv.1805.00675
arXiv: 1805.00675

[13] M. Kieferová, A. Scherer und DW Berry, Simulation der Dynamik zeitabhängiger Hamiltonianer mit einer verkürzten Dyson-Reihe, Physical Review A 99 (2019) 042314.
https: / / doi.org/ 10.1103 / PhysRevA.99.042314

[14] GH Low und IL Chuang, Hamiltonian Simulation by Qubitization, Quantum 3 (2019) 163.
https:/​/​doi.org/​10.22331/​q-2019-07-12-163

[15] R. Babbush, C. Gidney, DW Berry, N. Wiebe, J. McClean, A. Paler et al., Codierung elektronischer Spektren in Quantenschaltungen mit linearer t-Komplexität, Physical Review X 8 (2018) 041015.
https://doi.org/ 10.1103/PhysRevX.8.041015

[16] DW Berry, G. Ahokas, R. Cleve und BC Sanders, Effiziente Quantenalgorithmen zur Simulation spärlicher Hamiltonianer, Communications in Mathematical Physics 270 (2006) 359–371.
https: / / doi.org/ 10.1007 / s00220-006-0150-x

[17] N. Wiebe, DW Berry, P. Høyer und BC Sanders, Simulation der Quantendynamik auf einem Quantencomputer, Journal of Physics A: Mathematical and Theoretical 44 (2011) 445308.
https:/​/​doi.org/​10.1088/​1751-8113/​44/​44/​445308

[18] AM Childs, Y. Su, MC Tran, N. Wiebe und S. Zhu, Theorie des Traberfehlers mit Kommutatorskalierung, Physical Review X 11 (2021) 011020.
https://doi.org/ 10.1103/PhysRevX.11.011020

[19] J. Haah, MB Hastings, R. Kothari und GH Low, Quantenalgorithmus zur Simulation der Echtzeitentwicklung von Gitter-Hamiltonianern, SIAM Journal on Computing (2021) FOCS18.
https: / / doi.org/ 10.1137 / 18M12315

[20] M. Hagan und N. Wiebe, Zusammengesetzte Quantensimulationen, arXiv:2206.06409 (2022).
https:/​/​doi.org/​10.22331/​q-2023-11-14-1181
arXiv: 2206.06409

[21] GH Low, Y. Su, Y. Tong und MC Tran, Zur Komplexität der Implementierung von Traberschritten, arXiv:2211.09133 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.4.020323
arXiv: 2211.09133

[22] GH Low und IL Chuang, Optimale Hamilton-Simulation durch Quantensignalverarbeitung, Physical Review Letters 118 (2017).
https://doi.org/ 10.1103/physrevlett.118.010501

[23] S. Endo, Q. Zhao, Y. Li, S. Benjamin und X. Yuan, Mitigating algorithmicerrors in a hamiltonian simulation, Phys. Rev. A 99 (2019) 012334.
https: / / doi.org/ 10.1103 / PhysRevA.99.012334

[24] AC Vazquez, R. Hiptmair und S. Woerner, Verbesserung des Quantenlinearsystemalgorithmus mithilfe der Richardson-Extrapolation, ACM Transactions on Quantum Computing 3 (2022).
https: / / doi.org/ 10.1145 / 3490631

[25] AC Vazquez, DJ Egger, D. Ochsner und S. Woerner, Gut konditionierte Mehrproduktformeln für hardwarefreundliche Hamilton-Simulation, Quantum 7 (2023) 1067.
https:/​/​doi.org/​10.22331/​q-2023-07-25-1067

[26] M. Suzuki, Allgemeine Theorie fraktaler Pfadintegrale mit Anwendungen auf Vielteilchentheorien und statistische Physik, Journal of Mathematical Physics 32 (1991) 400.
https: / / doi.org/ 10.1063 / 1.529425

[27] A. Gilyén, Y. Su, GH Low und N. Wiebe, Quantum Singular Value Transformation and Beyond: Exponential Improvements for Quantum Matrix Arithmetics, in Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, S. 193–204, 2019 , DOI.
https: / / doi.org/ 10.1145 / 3313276.3316366

[28] C. Yi und E. Crosson, Spektralanalyse von Produktformeln für die Quantensimulation, npj Quantum Information 8 (2022) 37.
https: / / doi.org/ 10.1038 / s41534-022-00548-w

[29] A. Quarteroni, R. Sacco und F. Saleri, Numerische Mathematik, vol. 37, Springer Science & Business Media (2010), 10.1007/​b98885.
https: / / doi.org/ 10.1007 / b98885

[30] F. Piazzon und M. Vianello, Stabilitätsungleichungen für Lebesgue-Konstanten über Markov-ähnliche Ungleichungen, Dolomites Research Notes on Approximation 11 (2018).

[31] AP de Camargo, Zur numerischen Stabilität der Newton-Formel für die Lagrange-Interpolation, Journal of Computational and Applied Mathematics 365 (2020) 112369.
https://​/​doi.org/​10.1016/​j.cam.2019.112369

[32] L. Trefethen, Sechs Mythen der Polynominterpolation und Quadratur, (2011).

[33] W. Gautschi, Wie (in)stabil sind Vandermonde-Systeme? Asymptotische und rechnerische Analyse, in Lecture Notes in Pure and Applied Mathematics, S. 193–210, Marcel Dekker, Inc, 1990.

[34] NJ Higham, Die numerische Stabilität der baryzentrischen Lagrange-Interpolation, IMA Journal of Numerical Analysis 24 (2004) 547.
https://​/​doi.org/​10.1093/​imanum/​24.4.547

[35] JC Mason und DC Handscomb, Chebyshev polynomials, CRC press (2002), 10.1201/​9781420036114.
https: / / doi.org/ 10.1201 / 9781420036114

[36] G. Rendon, T. Izubuchi und Y. Kikuchi, Auswirkungen des Kosinus-Tapering-Fensters auf die Quantenphasenschätzung, Physical Review D 106 (2022) 034503.
https://doi.org/ 10.1103/PhysRevD.106.034503

[37] LN Trefethen, Approximation Theory and Approximation Practice, Extended Edition, SIAM (2019), 10.1137/​1.9781611975949.
https: / / doi.org/ 10.1137 / 1.9781611975949

[38] FL Bauer und CT Fike, Normen und Ausschlusssätze, Numer. Mathematik. 2 (1960) 137–141.
https: / / doi.org/ 10.1007 / BF01386217

[39] S. Blanes, F. Casas, J.-A. Oteo und J. Ros, Die Magnus-Erweiterung und einige ihrer Anwendungen, Physics Reports 470 (2009) 151.
https://doi.org/ 10.1016/j.physrep.2008.11.001

[40] N. Klco und MJ Savage, Minimal verschränkte Zustandsvorbereitung lokalisierter Wellenfunktionen auf Quantencomputern, Physical Review A 102 (2020).
https: / / doi.org/ 10.1103 / physreva.102.012612

[41] JJ García-Ripoll, Quanteninspirierte Algorithmen für die multivariate Analyse: von der Interpolation zu partiellen Differentialgleichungen, Quantum 5 (2021) 431.
https:/​/​doi.org/​10.22331/​q-2021-04-15-431

[42] W. Górecki, R. Demkowicz-Dobrzański, HM Wiseman und DW Berry, $pi$-korrigiertes Heisenberg-Limit, Physical Review Letters 124 (2020) 030501.
https://doi.org/ 10.1103/PhysRevLett.124.030501

[43] D. Grinko, J. Gacon, C. Zoufal und S. Woerner, Iterative Quantenamplitude Estimation, npj Quantum Information 7 (2021) 52 [1912.05559].
https:/​/​doi.org/​10.1038/​s41534-021-00379-1
arXiv: 1912.05559

[44] N. Wiebe, D. Berry, P. Høyer und BC Sanders, Zerlegungen höherer Ordnung geordneter Operator-Exponentialfunktionen, Journal of Physics A: Mathematical and Theoretical 43 (2010) 065203.
https:/​/​doi.org/​10.1088/​1751-8113/​43/​6/​065203

[45] RA Horn und CR Johnson, Matrix Analysis, Cambridge University Press (2012), 10.1017/​CBO9780511810817.
https: / / doi.org/ 10.1017 / CBO9780511810817

[46] M. Chiani, D. Dardari und MK Simon, Neue Exponentialgrenzen und Approximationen für die Berechnung der Fehlerwahrscheinlichkeit in Fading Channels, IEEE Transactions on Wireless Communications 2 (2003) 840.
https://​/​doi.org/​10.1109/​TWC.2003.814350

[47] JM Borwein und PB Borwein, Pi und die Hauptversammlung: eine Studie zur analytischen Zahlentheorie und zur Rechenkomplexität, Wiley-Interscience (1987).

[48] BL Higgins, DW Berry, SD Bartlett, HM Wiseman und GJ Pryde, Verschränkungsfreie Heisenberg-begrenzte Phasenschätzung, Nature 450 (2007) 393.
https: / / doi.org/ 10.1038 / nature06257

[49] RB Griffiths und C.-S. Niu, Semiclassical Fourier Transform for Quantum Computation, Physical Review Letters 76 (1996) 3228.
https://doi.org/ 10.1103/PhysRevLett.76.3228

[50] AY Kitaev, Quantenmessungen und das abelsche Stabilisatorproblem, quant-ph/​9511026 (1995).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9511026
arXiv: quant-ph / 9511026

[51] DS Abrams und S. Lloyd, Quantenalgorithmus, der eine exponentielle Geschwindigkeitssteigerung beim Finden von Eigenwerten und Eigenvektoren ermöglicht, Physical Review Letters 83 (1999) 5162.
https://doi.org/ 10.1103/PhysRevLett.83.5162

[52] J. Watkins, N. Wiebe, A. Roggero und D. Lee, Zeitabhängige Hamilton-Simulation unter Verwendung diskreter Uhrenkonstruktionen, arXiv:2203.11353 (2022).
https://​/​doi.org/​10.48550/​arXiv.2203.11353
arXiv: 2203.11353

[53] TD Ahle, Scharfe und einfache Grenzen für die Rohmomente der Binomial- und Poisson-Verteilungen, Statistics & Probability Letters 182 (2022) 109306.
https://​/​doi.org/​10.1016/​j.spl.2021.109306

[54] T. Rivlin, Chebyshev Polynomials, Dover Books on Mathematics, Dover Publications (2020).

Zitiert von

[1] Dean Lee, „Quantentechniken für Eigenwertprobleme“, European Physical Journal A 59 11, 275 (2023).

[2] Tatsuhiko N. Ikeda, Hideki Kono und Keisuke Fujii, „Trotter24: Eine präzisionsgarantierte adaptive Stufengrößen-Trotterisierung für Hamilton-Simulationen“, arXiv: 2307.05406, (2023).

[3] Hans Hon Sang Chan, Richard Meister, Matthew L. Goh und Bálint Koczor, „Algorithmic Shadow Spectroscopy“, arXiv: 2212.11036, (2022).

[4] Sergiy Zhuk, Niall Robertson und Sergey Bravyi, „Trotter-Fehlergrenzen und dynamische Mehrproduktformeln für die Hamilton-Simulation“, arXiv: 2306.12569, (2023).

[5] Zhicheng Zhang, Qisheng Wang und Mingsheng Ying, „Parallel Quantum Algorithm for Hamiltonian Simulation“, Quantum 8, 1228 (2024).

[6] Lea M. Trenkwalder, Eleanor Scerri, Thomas E. O'Brien und Vedran Dunjko, „Zusammenstellung der Produktformel-Hamiltonian-Simulation durch Verstärkungslernen“, arXiv: 2311.04285, (2023).

[7] Gumaro Rendon und Peter D. Johnson, „Low- Depth Gaussian State Energy Estimation“, arXiv: 2309.16790, (2023).

[8] Gregory Boyd, „Low-Overhead Parallelization of LCU via Commuting Operators“, arXiv: 2312.00696, (2023).

Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2024, 02:27:02 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.

On Der von Crossref zitierte Dienst Es wurden keine Daten zum Zitieren von Werken gefunden (letzter Versuch 2024-02-27 02:40:24).

Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.

Zeitstempel:

Mehr von Quantenjournal