1NTT Communication Science Laboratories, NTT Corporation, 3-1 Morinosato Wakamiya, Atsugi, Kanagawa 243-0198, Japan
2Fakultät für Informatik, Universität Gunma, 4-2 Aramakimachi, Maebashi, Gunma 371-8510, Japan
3Yukawa-Institut für Theoretische Physik, Universität Kyoto, Kitashirakawa Oiwakecho, Sakyo-ku, Kyoto 606-8502, Japan
4International Research Frontiers Initiative (IRFI), Tokyo Institute of Technology, Japan
Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.
Abstrakt
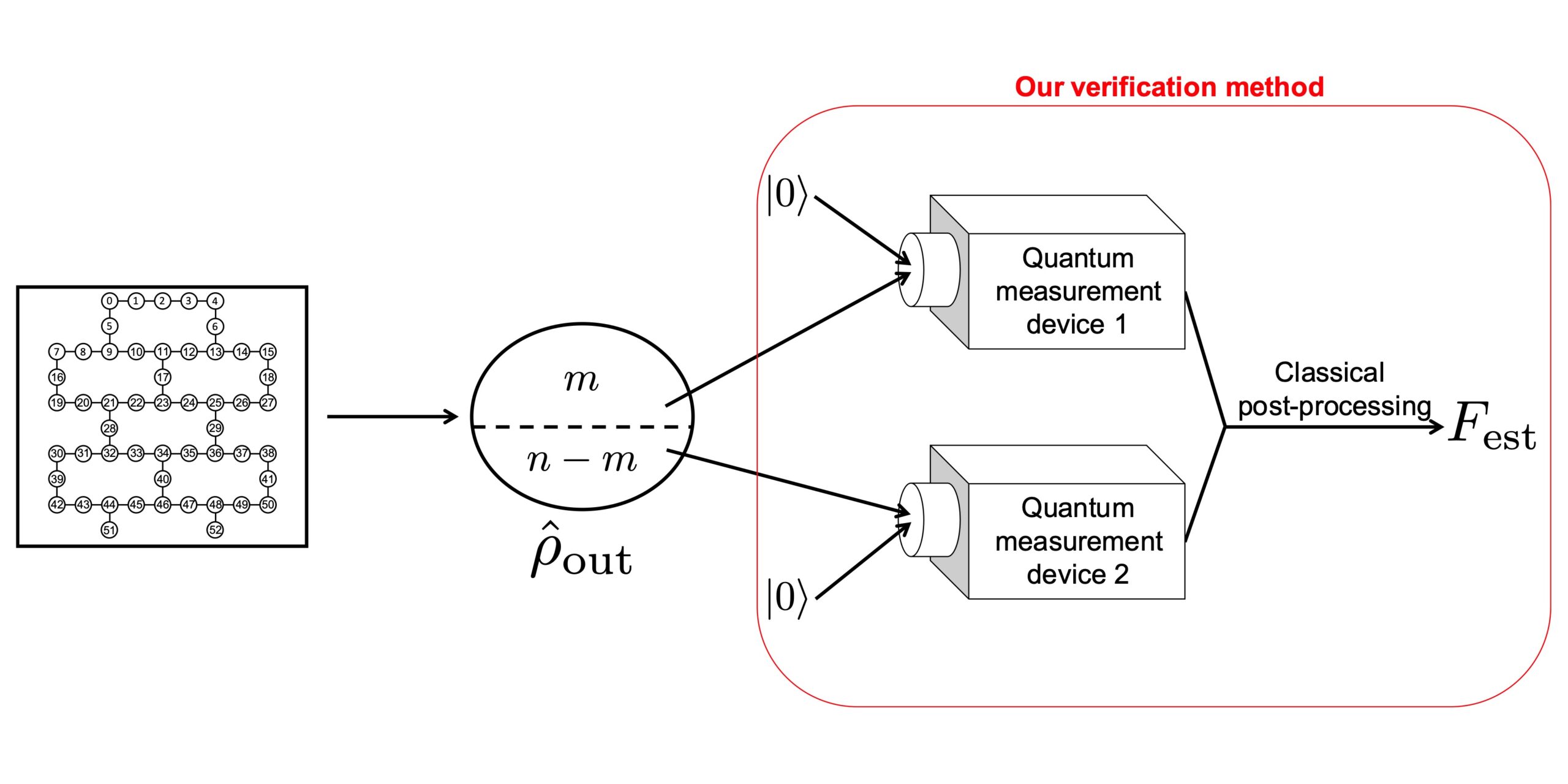
Mehrere verrauschte Quantenberechnungen im mittleren Maßstab können als Quantenschaltungen mit logarithmischer Tiefe auf einem spärlich besetzten Quantencomputerchip betrachtet werden, wobei Zwei-Qubit-Gatter nur auf einige Paare von Qubits direkt angewendet werden können. In diesem Artikel schlagen wir eine Methode vor, um eine solche verrauschte Quantenberechnung im mittleren Maßstab effizient zu verifizieren. Zu diesem Zweck charakterisieren wir zunächst kleinräumige Quantenoperationen in Bezug auf die Diamantnorm. Mithilfe dieser charakterisierten Quantenoperationen schätzen wir dann die Genauigkeit $langlepsi_t|hat{rho}_{rm out}|psi_trangle$ zwischen einem tatsächlichen $n$-Qubit-Ausgabezustand $hat{rho}_{rm out}$, der von erhalten wurde die verrauschte Quantenberechnung im mittleren Maßstab und der ideale Ausgabezustand (dh der Zielzustand) $|psi_trangle$. Obwohl die Methode der direkten Wiedergabetreue im Durchschnitt $O(2^n)$ Kopien von $hat{rho}_{rm out}$ erfordert, benötigt unsere Methode selbst in nur $O(D^32^{12D})$ Kopien Im schlimmsten Fall ist $D$ die Dichte von $|psi_tangle$. Für Quantenschaltungen mit logarithmischer Tiefe auf einem Chip mit geringer Dichte beträgt $D$ höchstens $O(log{n})$, und daher ist $O(D^32^{12D})$ ein Polynom in $n$. Mithilfe des IBM Manila 5-Qubit-Chips führen wir außerdem ein Proof-of-Principe-Experiment durch, um die praktische Leistung unserer Methode zu beobachten.
► BibTeX-Daten
► Referenzen
[1] J. Preskill, Quantum Computing in der NISQ-Ära und darüber hinaus, Quantum 2, 79 (2018).
https://doi.org/10.22331/q-2018-08-06-79
[2] A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, PJ Love, A. Aspuru-Guzik und JL O'Brien, Ein Variationseigenwertlöser auf einem photonischen Quantenprozessor, Nat. Komm. 5, 4213 (2014).
https: / / doi.org/ 10.1038 / ncomms5213
[3] E. Farhi, J. Goldstone und S. Gutmann, A Quantum Approximate Optimization Algorithm, arXiv:1411.4028.
https:///doi.org/10.48550/arxiv.1411.4028
arXiv: 1411.4028
[4] K. Mitarai, M. Negoro, M. Kitagawa und K. Fujii, Quantum Circuit Learning, Phys. Rev. A 98, 032309 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032309
[5] A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, JM Chow und JM Gambetta, Hardware-effizienter Variationsquanteneigenlöser für kleine Moleküle und Quantenmagnete, Nature (London) 549, 242 (2017) .
https: / / doi.org/ 10.1038 / nature23879
[6] V. Havlíček, AD Córcoles, K. Temme, AW Harrow, A. Kandaka, JM Chow und JM Gambetta, Überwachtes Lernen mit quantenverstärkten Merkmalsräumen, Nature (London) 567, 209 (2019).
https://doi.org/10.1038/s41586-019-0980-2
[7] Y. Li und SC Benjamin, Effizienter Variationsquantensimulator mit aktiver Fehlerminimierung, Phys. Rev. X 7, 021050 (2017).
https://doi.org/ 10.1103/PhysRevX.7.021050
[8] K. Temme, S. Bravyi und JM Gambetta, Fehlerminderung für kurztiefe Quantenschaltungen, Phys. Rev. Lett. 119, 180509 (2017).
https://doi.org/ 10.1103/PhysRevLett.119.180509
[9] S. Endo, SC Benjamin und Y. Li, Praktische Quantenfehlerminderung für Anwendungen in naher Zukunft, Phys. Rev. X 8, 031027 (2018).
https://doi.org/ 10.1103/PhysRevX.8.031027
[10] VN Premakumar und R. Joynt, Fehlerminderung in Quantencomputern, die räumlich korreliertem Rauschen unterliegen, arXiv:1812.07076.
https:///doi.org/10.48550/arxiv.1812.07076
arXiv: 1812.07076
[11] X. Bonet-Monroig, R. Sagastizabal, M. Singh und TE O'Brien, Kostengünstige Fehlerminderung durch Symmetrieverifizierung, Phys. Rev. A 98, 062339 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.062339
[12] J. Sun, X. Yuan, T. Tsunoda, V. Vedral, SC Benjamin und S. Endo, Mitigating Realistic Noise in Practical Noisy Intermediate-Scale Quantum Devices, Phys. Rev. Applied 15, 034026 (2021).
https: / / doi.org/ 10.1103 / PhysRevApplied.15.034026
[13] X.-M. Zhang, W. Kong, MU Farooq, M.-H. Yung, G. Guo und X. Wang, Generische erkennungsbasierte Fehlerminderung mithilfe von Quanten-Autoencodern, Phys. Rev. A 103, L040403 (2021).
https:///doi.org/10.1103/PhysRevA.103.L040403
[14] A. Strikis, D. Qin, Y. Chen, SC Benjamin und Y. Li, Learning-Based Quantum Error Mitigation, PRX Quantum 2, 040330 (2021).
https: / / doi.org/ 10.1103 / PRXQuantum.2.040330
[15] P. Czarnik, A. Arrasmith, PJ Coles und L. Cincio, Fehlerminderung mit Clifford-Quantum-Circuit-Daten, Quantum 5, 592 (2021).
https://doi.org/10.22331/q-2021-11-26-592
[16] A. Zlokapa und A. Gheorghiu, Ein Deep-Learning-Modell zur Rauschvorhersage auf kurzfristigen Quantengeräten, arXiv:2005.10811.
https:///doi.org/10.48550/arxiv.2005.10811
arXiv: 2005.10811
[17] K. Yeter-Aydeniz, RC Pooser und G. Siopsis, Praktische Quantenberechnung chemischer und nuklearer Energieniveaus unter Verwendung der imaginären Quantenzeitentwicklung und Lanczos-Algorithmen, npj Quantum Information 6, 63 (2020).
https://doi.org/10.1038/s41534-020-00290-1
[18] B. Tan und J. Cong, Optimality Study of Existing Quantum Computing Layout Synthesis Tools, IEEE Transactions on Computers 70, 1363 (2021).
https: / / doi.org/ 10.1109 / TC.2020.3009140
[19] MR Perelshtein, AI Pakhomchik, AA Melnikov, AA Novikov, A. Glatz, GS Paraoanu, VM Vinokur und GB Lesovik, Solving Large-Scale Linear Systems of Equations by a Quantum Hybrid Algorithm, Ann. Physik. 2200082 (2022).
https: / / doi.org/ 10.1002 / andp.202200082
[20] A. Kondratyev, Nicht-differenzierbares Lernen einer durch Quantenschaltkreise geborenen Maschine mit genetischem Algorithmus, Wilmott 2021, 50 (2021).
https:///doi.org/10.1002/wilm.10943
[21] S. Dasgupta, KE Hamilton und A. Banerjee, Charakterisierung der Speicherkapazität von Transmon-Qubit-Reservoirs, arXiv:2004.08240.
https:///doi.org/10.48550/arxiv.2004.08240
arXiv: 2004.08240
[22] LM Sager, SE Smart, DA Mazziotti, Vorbereitung eines Exzitonenkondensats von Photonen auf einem 53-Qubit-Quantencomputer, Phys. Rev. Research 2, 043205 (2020).
https: / / doi.org/ 10.1103 / PhysRevResearch.2.043205
[23] JR Wootton, Ein Quantenverfahren zur Kartenerzeugung, in Proc. der 2020 IEEE Conference on Games (IEEE, Osaka, 2020), S. 73.
https:///doi.org/10.1109/CoG47356.2020.9231571
[24] W J. Huang, W.-C. Chien, C.-H. Cho, C.-C. Huang, T.-W. Huang und C.-R. Chang, Mermins Ungleichungen mehrerer Qubits mit orthogonalen Messungen am IBM Q 53-Qubit-System, Quantum Engineering 2, e45 (2020).
https:///doi.org/10.1002/que2.45
[25] T. Morimae, Verifizierung für rein messtechnisches blindes Quantencomputing, Phys. Rev. A 89, 060302(R) (2014).
https: / / doi.org/ 10.1103 / PhysRevA.89.060302
[26] M. Hayashi und T. Morimae, Verifiable Measurement-only Blind Quantum Computing with Stabilizer Testing, Phys. Rev. Lett. 115, 220502 (2015).
https://doi.org/ 10.1103/PhysRevLett.115.220502
[27] T. Morimae, Nur durch Messung überprüfbares blindes Quantencomputing mit Quanteneingabeverifizierung, Phys. Rev. A 94, 042301 (2016).
https: / / doi.org/ 10.1103 / PhysRevA.94.042301
[28] D. Aharonov, M. Ben-Or, E. Eban und U. Mahadev, Interactive Proofs for Quantum Computations, arXiv:1704.04487.
https:///doi.org/10.48550/arxiv.1704.04487
arXiv: 1704.04487
[29] JF Fitzsimons und E. Kashefi, Bedingungslos überprüfbare blinde Quantenberechnung, Phys. Rev. A 96, 012303 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.012303
[30] T. Morimae, Y. Takeuchi und M. Hayashi, Verification of Hypergraph States, Phys. Rev. A 96, 062321 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.062321
[31] JF Fitzsimons, M. Hajdušek und T. Morimae, Post-hoc-Verifizierung der Quantenberechnung, Phys. Rev. Lett. 120, 040501 (2018).
https://doi.org/ 10.1103/PhysRevLett.120.040501
[32] Y. Takeuchi und T. Morimae, Verification of Many-Qubit States, Phys. Rev. X 8, 021060 (2018).
https://doi.org/ 10.1103/PhysRevX.8.021060
[33] A. Broadbent, How to Verify a Quantum Computation, Theory of Computing 14, 11 (2018).
https: / / doi.org/ 10.4086 / toc.2018.v014a011
[34] U. Mahadev, Classical Verification of Quantum Computations, in Proc. des 59. jährlichen Symposiums über Grundlagen der Informatik (IEEE, Paris, 2018), S. 259.
https:///doi.ieeecomputersociety.org/10.1109/FOCS.2018.00033
[35] Y. Takeuchi, A. Mantri, T. Morimae, A. Mizutani und JF Fitzsimons, Ressourceneffiziente Verifizierung des Quantencomputings mithilfe der Serfling-Grenze, npj Quantum Information 5, 27 (2019).
https://doi.org/10.1038/s41534-019-0142-2
[36] M. Hayashi und Y. Takeuchi, Verifying pendelnde Quantenberechnungen mittels Fidelity Estimation of Weighted Graph States, New J. Phys. 21, 093060 (2019).
https://doi.org/10.1088/1367-2630/ab3d88
[37] A. Gheorghiu und T. Vidick, Computationally-Secure and Composable Remote State Prepared, in Proc. des 60. jährlichen Symposiums zu Grundlagen der Informatik (IEEE, Baltimore, 2019), S. 1024.
https: / / doi.org/ 10.1109 / FOCS.2019.00066
[38] G. Alagic, AM Childs, AB Grilo und S.-H. Hung, Nicht-interaktive klassische Verifizierung der Quantenberechnung, in Proc. of Theory of Cryptography Conference (Springer, Virtual, 2020), S. 153.
https://doi.org/10.1007/978-3-030-64381-2_6
[39] H. Zhu und M. Hayashi, Efficient Verification of Hypergraph States, Phys. Rev. Applied 12, 054047 (2019).
https: / / doi.org/ 10.1103 / PhysRevApplied.12.054047
[40] N.-H. Chia, K.-M. Chung und T. Yamakawa, Classical Verification of Quantum Computations with Efficient Verifier, in Proc. of Theory of Cryptography Conference (Springer, Virtual, 2020), S. 181.
https://doi.org/10.1007/978-3-030-64381-2_7
[41] D. Markham und A. Krause, A Simple Protocol for Certifying Graph States and Applications in Quantum Networks, Cryptography 4, 3 (2020).
https: / / doi.org/ 10.3390 / cryptography4010003
[42] R. Raussendorf und HJ Briegel, Ein Einweg-Quantencomputer, Phys. Rev. Lett. 86, 5188 (2001).
https://doi.org/ 10.1103/PhysRevLett.86.5188
[43] O. Regev, Über Gitter, Lernen mit Fehlern, zufällige lineare Codes und Kryptographie, Journal of the ACM 56, 34 (2009).
https: / / doi.org/ 10.1145 / 1568318.1568324
[44] Wenn $n$-Qubit-Quantenoperationen erlaubt sind, ist die effiziente Verifizierung trivial möglich. Sei $U$ ein einheitlicher Operator mit $|psi_trangle=U|0^nrangle$ für einen idealen Ausgabezustand $|psi_trangle$. Wir wenden $U^†$ auf einen empfangenen Zustand $hat{rho}$ an und messen alle Qubits in der Rechenbasis. Dann können wir durch Abschätzen der Wahrscheinlichkeit, dass $0^n$ beobachtet wird, die Genauigkeit $langle 0^n|U^†hat{rho}U|0^nrangle$ zwischen $|psi_trangle$ und $hat{rho}$ abschätzen .
[45] Der Klarheit halber verwenden wir die Notation $hat{a}$, wenn der Kleinbuchstabe $a$ ein Quantenzustand oder eine Quantenoperation ist. Andererseits lassen wir für jeden Großbuchstaben $A$ $hat{color{white}{a}}$ weg, selbst wenn $A$ ein Quantenzustand oder eine Quantenoperation ist.
[46] DT Smithey, M. Beck, MG Raymer und A. Faridani, Messung der Wigner-Verteilung und der Dichtematrix eines Lichtmodus mithilfe optischer Homodyn-Tomographie: Anwendung auf gequetschte Zustände und das Vakuum, Phys. Rev. Lett. 70, 1244 (1993).
https://doi.org/ 10.1103/PhysRevLett.70.1244
[47] Z. Hradil, Quantenzustandsschätzung, Phys. Rev. A 55, R1561(R) (1997).
https: / / doi.org/ 10.1103 / PhysRevA.55.R1561
[48] K. Banaszek, GM D'Ariano, MGA Paris und MF Sacchi, Maximum-Likelihood-Schätzung der Dichtematrix, Phys. Rev. A 61, 010304(R) (1999).
https: / / doi.org/ 10.1103 / PhysRevA.61.010304
[49] ST Flammia und Y.-K. Liu, Direct Fidelity Estimation from Few Pauli Measurements, Phys. Rev. Lett. 106, 230501 (2011).
https://doi.org/ 10.1103/PhysRevLett.106.230501
[50] S. Ferracin, T. Kapourniotis und A. Datta, Accrediting Outputs of Noisy Intermediate-Scale Quantum Computing Devices, New J. Phys. 21 113038 (2019).
https://doi.org/10.1088/1367-2630/ab4fd6
[51] S. Ferracin, ST Merkel, D. McKay und A. Datta, Experimentelle Akkreditierung der Ergebnisse verrauschter Quantencomputer, Phys. Rev. A 104, 042603 (2021).
https: / / doi.org/ 10.1103 / PhysRevA.104.042603
[52] D. Leichtle, L. Music, E. Kashefi und H. Ollivier, Verifying BQP Computations on Noisy Devices with Minimal Overhead, PRX Quantum 2, 040302 (2021).
https: / / doi.org/ 10.1103 / PRXQuantum.2.040302
[53] Y.-C. Liu, X.-D. Yu, J. Shang, H. Zhu und X. Zhang, Efficient Verification of Dicke States, Phys. Rev. Applied 12, 044020 (2019).
https: / / doi.org/ 10.1103 / PhysRevApplied.12.044020
[54] S. Bravyi, G. Smith und JA Smolin, Trading Classical and Quantum Computational Resources, Phys. Rev. X 6, 021043 (2016).
https://doi.org/ 10.1103/PhysRevX.6.021043
[55] T. Peng, A. Harrow, M. Ozols und X. Wu, Simulation großer Quantenschaltkreise auf einem kleinen Quantencomputer, Phys. Rev. Lett. 125, 150504 (2020).
https://doi.org/ 10.1103/PhysRevLett.125.150504
[56] D. Aharonov, A. Kitaev und N. Nisan, Quantum Circuits with Mixed States, in Proc. des 30. jährlichen ACM-Symposiums zur Computertheorie (ACM, Dallas, 1998), S. 20.
https: / / doi.org/ 10.1145 / 276698.276708
[57] MA Nielsen und IL Chuang, Quantum Computation and Quantum Information 10th Anniversary Edition (Cambridge University Press, Cambridge, 2010).
https: / / doi.org/ 10.1017 / CBO9780511976667
[58] M. Fanciulli, Hrsg., Electron Spin Resonance and Related Phenomena in Low-Dimensional Structures (Springer, Berlin, 2009).
https://doi.org/10.1007/978-3-540-79365-6
[59] W. Hoeffding, Probability Inequalities for Sums of Bounded Random Variables, Journal of the American Statistical Association 58, 13 (1963).
https:///www.tandfonline.com/doi/ref/10.1080/01621459.1963.10500830?scroll=top
[60] K. Li und G. Smith, Quantum-de-Finetti-Theorem unter vollständig einseitig adaptiven Messungen, Phys. Rev. Lett. 114, 160503 (2015).
https://doi.org/ 10.1103/PhysRevLett.114.160503
[61] F. Arute, K. Arya, R. Babbush, D. Bacon, JC Bardin, R. Barends, R. Biswas, S. Boixo, FGSL Brandao, DA Buell, B. Burkett, Y. Chen, Z. Chen, B . Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, MP Harrigan, MJ Hartmann, A. Ho, M. Hoffmann, T. Huang, TS Humble, SV Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, PV Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, JR McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J . Mutus, O. Naaman, M. Neeley, C. Neill, MY Niu, E. Ostby, A. Petukhov, JC Platt, C. Quintana, EG Rieffel, P. Roushan, NC Rubin, D. Sank, KJ Satzinger, V. Smelyanskiy, KJ Sung, MD Trevithick, A. Vainsencher, B. Villalonga, T. White, ZJ Yao, P. Yeh, A. Zalcman, H. Neven und JM Martinis, Quantenüberlegenheit mit einem programmierbaren supraleitenden Prozessor, Nature (London) 574, 505 (2019).
https://doi.org/10.1038/s41586-019-1666-5
[62] RJ Lipton und RE Tarjan, A Separator Theorem for Planar Graphs, SIAM J. Appl. Mathematik. 36, 177 (1979).
https: / / doi.org/ 10.1137 / 0136016
[63] RJ Lipton und RE Tarjan, Applications of a Planar Separator Theorem, SIAM J. Comput. 9, 615 (1980).
https: / / doi.org/ 10.1137 / 0209046
[64] K. Fujii, K. Mizuta, H. Ueda, K. Mitarai, W. Mizukami, YO Nakagawa, Deep Variational Quantum Eigensolver: Eine Divide-and-Conquer-Methode zur Lösung eines größeren Problems mit kleineren Quantencomputern, PRX Quantum 3, 010346 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010346
[65] W. Tang, T. Tomesh, M. Suchara, J. Larson und M. Martonosi, CutQC: Verwendung kleiner Quantencomputer für die Auswertung großer Quantenschaltungen, in Proc. der 26. ACM International Conference on Architectural Support for Programming Languages and Operating Systems (ACM, Virtual, 2021), S. 473.
https: / / doi.org/ 10.1145 / 3445814.3446758
[66] K. Mitarai und K. Fujii, Constructing a Virtual Two-Qubit Gate by Sampling Single-Qubit Operations, New J. Phys. 23, 023021 (2021).
https: / / doi.org/ 10.1088 / 1367-2630 / abd7bc
[67] K. Mitarai und K. Fujii, Overhead für die Simulation eines nicht-lokalen Kanals mit lokalem Kanal durch Quasi-Probability-Sampling, Quantum 5, 388 (2021).
https://doi.org/10.22331/q-2021-01-28-388
[68] MA Perlin, ZH Saleem, M. Suchara und JC Osborn, Quantum Circuit Cutting with Maximum-Likelihood Tomography, npj Quantum Information 7, 64 (2021).
https://doi.org/10.1038/s41534-021-00390-6
[69] T. Ayral, F.-M. L Régent, Z. Saleem, Y. Alexeev und M. Suchara, Quantum Divide and Compute: Hardware Demonstrations and Noisy Simulations, in Proc. des 2020 IEEE Computer Society Annual Symposium on VLSI (IEEE, Limassol, 2020), S. 138.
https:///doi.org/10.1109/ISVLSI49217.2020.00034
Zitiert von
[1] Ruge Lin und Weiqiang Wen, „Quantum Computation Capability Verification Protocol for Noisy Intermediate-Scale Quantum Devices with the Dieder Coset Problem“, Physische Überprüfung A 106 1, 012430 (2022).
[2] Ruge Lin und Weiqiang Wen, „Quantum Computation Capability Verification Protocol for NISQ Devices with Dieder Coset Problem“, arXiv: 2202.06984.
Die obigen Zitate stammen von Der von Crossref zitierte Dienst (zuletzt erfolgreich aktualisiert am 2022:07) und SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2022, 07:27:01 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.
Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.