Orthonormale Grundlagen extremer Quantität

Neuauflage von Plato

Verfolger: 0

Marcin Rudziński^1,2, Adam Burchardt³ und Karol Życzkowski^1,4

¹Fakultät für Physik, Astronomie und Angewandte Informatik, Jagiellonen-Universität, Ul. Łojasiewicza 11, 30-348 Krakau, Polen
²Doktoratsschule für Exakte und Naturwissenschaften, Jagiellonen-Universität, Ul. Łojasiewicza 11, 30-348 Krakau, Polen
³QuSoft, CWI und Universität Amsterdam, Science Park 123, 1098 XG Amsterdam, Niederlande
⁴Zentrum für Theoretische Physik, Polnische Akademie der Wissenschaften, Al. Lotników 32/46, 02-668 Warszawa, Polen

Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.

Abstrakt

Spin-antikohärente Zustände haben in letzter Zeit als die „quantenreichsten“ Zustände große Aufmerksamkeit erregt. Einige kohärente und antikohärente Spinzustände werden als optimale Quantenrotosensoren bezeichnet. In dieser Arbeit führen wir ein Quantenmaß für Orthonormalbasen von Spinzuständen ein, das durch die durchschnittliche Antikohärenz einzelner Vektoren und die Wehrl-Entropie bestimmt wird. Auf diese Weise identifizieren wir die kohärentesten und quantenreichsten Zustände, die zu orthogonalen Messungen extremer Quantenhaftigkeit führen. Ihre Symmetrien können mithilfe der Majorana-Sterndarstellung aufgedeckt werden, die eine intuitive geometrische Darstellung eines reinen Zustands durch Punkte auf einer Kugel bietet. Die erhaltenen Ergebnisse führen zu maximal (minimal) verschränkten Basen im $2j+1$-dimensionalen symmetrischen Unterraum des $2^{2j}$-dimensionalen Zustandsraums mehrteiliger Systeme, die aus $2j$-Qubits bestehen. Einige gefundene Basen sind isokohärent, da sie aus allen Zuständen mit dem gleichen Grad an Spinkohärenz bestehen.

Orthonormale Grundlagen extremer Quantenhaftigkeit PlatoBlockchain Data Intelligence. Vertikale Suche. Ai.

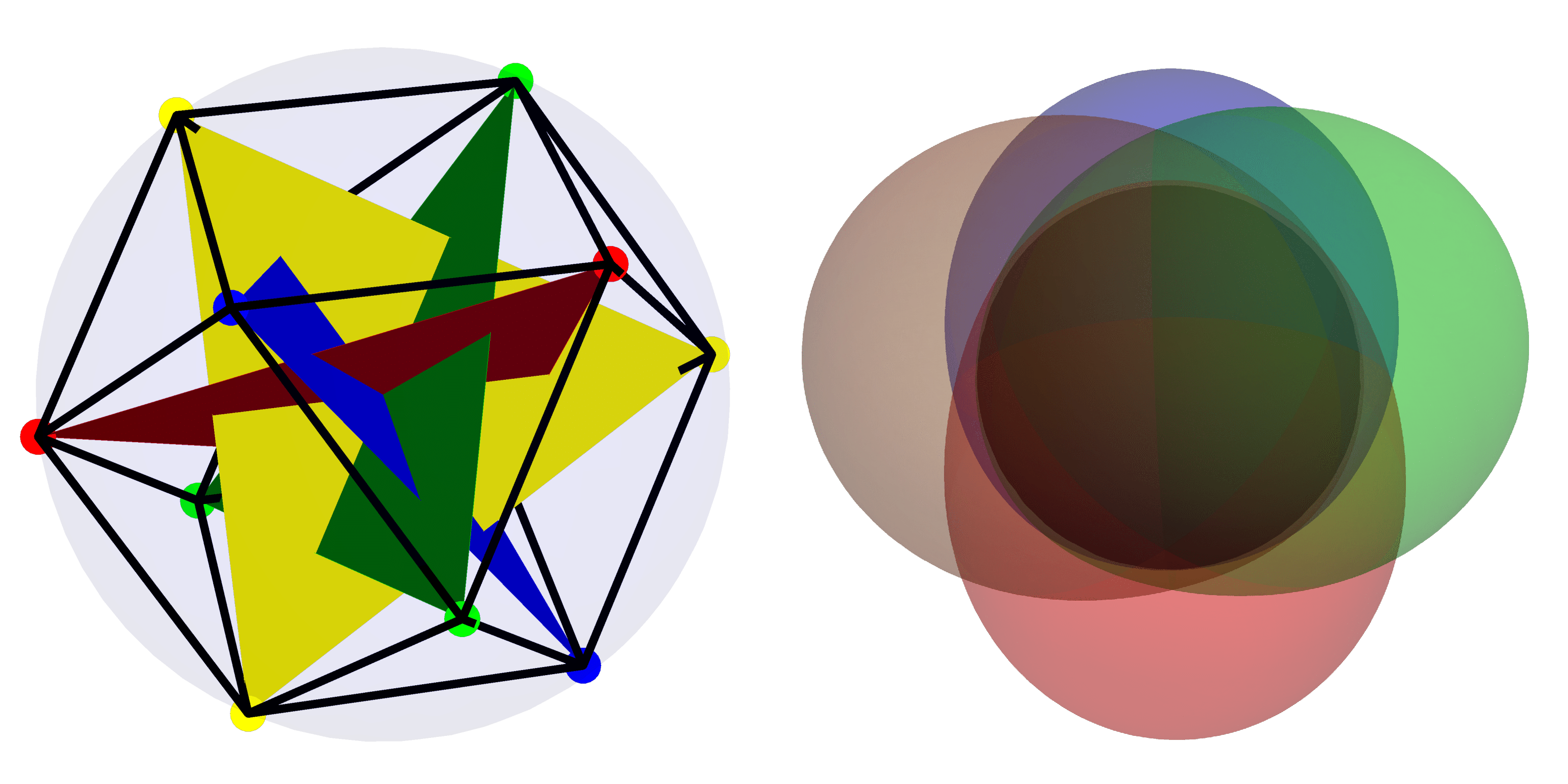
Ausgewähltes Bild: Im linken Bild wird die „quantenreichste“ Basis in $mathcal{H}_4$ anhand der Sterndarstellung dargestellt. Rechts ist die Husimi-Funktion für Zustände auf der kohärentesten („klassischen“) Basis innerhalb von $mathcal{H}_4$ dargestellt.

Populäre Zusammenfassung

Extremalzustände, kohärent und antikohärent, finden praktische Anwendungen in der Quantenmetrologie als optimale Rotosensoren. Diese Arbeit stellt eine natürliche Erweiterung früherer Studien zur Suche nach solchen Zuständen dar und schlägt optimale orthogonale Messungen der extremen Spinkohärenz nach Lüders und von Neumann vor. Wir führen das Maß $mathcal{B}_t$ als Werkzeug zur Charakterisierung der Quantität einer Messung ein, die durch eine Basis in $mathcal{H}_N$ gegeben ist. Die Suche nach den meisten Quantenbasen für $N=3,4,5$ und $7$ wird durchgeführt. Numerische Ergebnisse legen nahe, dass die erhaltenen Lösungen einzigartig sind. Für $N=3,4,5,6$ wird eine Reihe von Kandidaten für die „klassischen“ Basen angegeben, die aus den spinkohärentesten Zuständen bestehen. Einige der Quantenbasen, analysiert in der Sterndarstellung von Majorana, offenbaren Symmetrien platonischer Körper. Auch die meisten klassischen Basen weisen symmetrische Strukturen auf. Wir haben auch andere Maße der Quantität von Vektoren betrachtet, die eine gegebene Basis bilden. Die Optimierung der mittleren Wehrl-Entropie von $N$ orthogonalen Vektoren führt zu denselben Basen, die sich durch Extremalwerte der Größen $mathcal{B}_t$ unterscheiden, mit einer einzigen Ausnahme der Quantenbasis für $N=6$.

► BibTeX-Daten

@article{Rudzinski2024orthonormalbasesof, doi = {10.22331/q-2024-01-25-1234}, url = {https://doi.org/10.22331/q-2024-01-25-1234}, title = {Orthonormalbases von extremer Quantenhaftigkeit}, Autor = {Rudzi{'{n}}ski, Marcin und Burchardt, Adam und {.{Z}}yczkowski, Karol}, Zeitschrift = {{Quantum}}, issn = {2521-327X}, Herausgeber = {{Verein zur F{“{o}}rdung des Open Access Publizierens in den Quantenwissenschaften}}, Band = {8}, Seiten = {1234}, Monat = Jan, Jahr = {2024} }

► Referenzen

[1] T. Frankel, The Geometry of Physics: An Introduction, 3. Auflage, Cambridge University Press (2011).
https: / / doi.org/ 10.1017 / CBO9781139061377

[2] D. Chruściński und A. Jamiołkowski, Geometrische Phasen in der klassischen und Quantenmechanik, Birkhäuser (2004).
https://doi.org/10.1007/978-0-8176-8176-0

[3] DA Lee, Geometrische Relativitätstheorie, American Mathematical Society, Providence (2021).
https: / / doi.org/ 10.1090 / gsm / 201

[4] I. Bengtsson und K. Życzkowski, Geometry of Quantum States: An Introduction to Quantum Entanglement, 2. Auflage, Cambridge University Press (2017).
https: / / doi.org/ 10.1017 / 9781139207010

[5] M. Lewin, Geometrische Methoden für nichtlineare Vielteilchen-Quantensysteme, J. Functional Analysis 260, 12, (2011).
https: // doi.org/ 10.1016 / j.jfa.2010.11.017

[6] E. Cohen, H. Larocque, F. Bouchard et al., Geometrische Phase von Aharonov–Bohm bis Pancharatnam–Berry und darüber hinaus, Nat. Rev. Phys. 1, 437–449 (2019).
https://doi.org/10.1038/s42254-019-0071-1

[7] E. Majorana Atomi orientati in campo magneto variable, Nuovo Cimento 9, 43-50 (1932).
https: / / doi.org/ 10.1007 / BF02960953

[8] R. Barnett, A. Turner und E. Demler, Klassifizierung neuartiger Phasen von Spinoratomen, Phys. Rev. Lett. 97, 180412 (2006).
https://doi.org/ 10.1103/PhysRevLett.97.180412

[9] R. Barnett, A. Turner und E. Demler, Klassifizierung von Wirbeln in $S=3$ Bose-Einstein-Kondensaten, Phys. Rev. A 76, 013605 (2007).
https: / / doi.org/ 10.1103 / PhysRevA.76.013605

[10] H. Mäkelä und K.-A. Suominen, Inertzustände von Spin-s-Systemen, Phys. Rev. Lett. 99, 190408 (2007).
https://doi.org/ 10.1103/PhysRevLett.99.190408

[11] E. Serrano-Ensástiga und F. Mireles, Phasencharakterisierung von Spinor-Bose-Einstein-Kondensaten: ein Majorana-Sterndarstellungsansatz, Phys. Lette. A 492, 129188 (2023).
https: / / doi.org/ 10.1016 / j.physleta.2023.129188

[12] P. Mathonet et al., Verschränkungsäquivalenz symmetrischer $N$-Qubit-Zustände, Phys. Rev. A 81, 052315 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.052315

[13] J. Martin, O. Giraud, PA Braun, D. Braun und T. Bastin, Multiqubit symmetrische Zustände mit hoher geometrischer Verschränkung, Phys. Rev. A 81, 062347 (2010).
https: / / doi.org/ 10.1103 / PhysRevA.81.062347

[14] M. Aulbach, DJH Markham und M. Murao, Der maximal verschränkte symmetrische Zustand in Bezug auf das geometrische Maß, New J. Phys. 12, 073025 (2010).
https://doi.org/10.1088/1367-2630/12/7/073025

[15] DJH Markham, Verschränkung und Symmetrie in permutationssymmetrischen Zuständen, Phys. Rev. A 83, 042332 (2011).
https: / / doi.org/ 10.1103 / PhysRevA.83.042332

[16] P. Ribeiro und R. Mosseri, Verschränkung im symmetrischen Sektor von $n$-Qubits, Phys. Rev. Lett. 106, 180502 (2011).
https://doi.org/ 10.1103/PhysRevLett.106.180502

[17] M.Aulbach, Klassifikation der Verschränkung in symmetrischen Zuständen, Int. J. Quantum Inform. 10, 1230004 (2012).
https: / / doi.org/ 10.1142 / S0219749912300045

[18] W. Ganczarek, M. Kuś und K. Życzkowski, Baryzentrisches Maß der Quantenverschränkung, Phys. Rev. A 85, 032314 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.032314

[19] A. Mandilara, T. Coudreau, A. Keller und P. Milman, Verschränkungsklassifizierung reiner symmetrischer Zustände über spinkohärente Zustände, Phys. Rev. A 90, 050302(R) (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.050302

[20] P. Hyllus, et al., Fisher Information and Multiparticle Entanglement, Phys. Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[21] JH Hannay, Die Berry-Phase für den Spin in der Majorana-Darstellung, J. Phys. A: Mathe. Gen. 31, L53 (1998).
https://doi.org/10.1088/0305-4470/31/2/002

[22] P. Bruno, Quantengeometrische Phase in Majoranas Sterndarstellung: Abbildung auf eine Vielteilchen-Aharonov-Bohm-Phase, Phys. Rev. Lett. 108, 240402 (2012).
https://doi.org/ 10.1103/PhysRevLett.108.240402

[23] HD Liu und LB Fu, Berry-Phase und Quantenverschränkung in Majoranas Sterndarstellung, Phys. Rev. A 94, 022123 (2016).
https: / / doi.org/ 10.1103 / PhysRevA.94.022123

[24] P. Ribeiro, J. Vidal und R. Mosseri, Thermodynamische Grenze des Lipkin-Meshkov-Glick-Modells, Phys. Rev. Lett. 99, 050402 (2007).
https://doi.org/ 10.1103/PhysRevLett.99.050402

[25] P. Ribeiro, J. Vidal und R. Mosseri, Exaktes Spektrum des Lipkin-Meshkov-Glick-Modells im thermodynamischen Grenzfall und Korrekturen endlicher Größe, Phys. Rev. E 78, 021106 (2008).
https: / / doi.org/ 10.1103 / PhysRevE.78.021106

[26] J. Zimba, „Antikohärente“ Spinzustände über die Majorana-Darstellung, Electron. J. Theor. Physik. 3, 143 (2006).
https:///api.semanticsscholar.org/CorpusID:13938120

[27] D. Baguette, T. Bastin und J. Martin, Symmetrische Multiqubit-Zustände mit maximal gemischten Ein-Qubit-Reduktionen, Phys. Rev. A 90, 032314 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.032314

[28] O. Giraud, D. Braun, D. Baguette, T. Bastin und J. Martin, Tensordarstellung von Spinzuständen, Phys. Rev. Lett. 114, 080401 (2015).
https://doi.org/ 10.1103/PhysRevLett.114.080401

[29] D. Baguette, F. Damanet, O. Giraud und J. Martin, Antikohärenz von Spinzuständen mit Punktgruppensymmetrien, Phys. Rev. A 92, 052333 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.92.052333

[30] HD Liu, LB Fu, X. Wang, Kohärenter-Staats-Ansatz für die Majorana-Repräsentation, Commun. Theor. Physik. 67, 611 (2017).
https://doi.org/10.1088/0253-6102/67/6/611

[31] D. Baguette und J. Martin, Antikohärenzmaße für reine Spinzustände, Phys. Rev. A 96, 032304 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.96.032304

[32] P. Kolenderski und R. Demkowicz-Dobrzański, Optimaler Zustand für die Ausrichtung von Referenzsystemen und den platonischen Körpern, Phys. Rev. A 78, 052333 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052333

[33] C. Chryssomalakos und H. Hernández-Coronado, Optimale Quantenrotosensoren, Phys. Rev. A 95, 052125 (2017).
https: / / doi.org/ 10.1103 / PhysRevA.95.052125

[34] AZ Goldberg und DFV James, Quantenbegrenzte Euler-Winkelmessungen unter Verwendung antikohärenter Zustände, Phys. Rev. A 98, 032113 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032113

[35] J. Martin, S. Weigert und O. Giraud, Optimale Erkennung von Rotationen um unbekannte Achsen durch kohärente und antikohärente Zustände, Quantum 4, 285 (2020).
https://doi.org/10.22331/q-2020-06-22-285

[36] J. Crann, DW Kribs und R. Pereira, Sphärische Designs und antikohärente Spinzustände, J. Phys. A: Mathe. Theor. 43, 255307 (2010).
https://doi.org/10.1088/1751-8113/43/25/255307

[37] E. Bannai und M. Tagami, Eine Anmerkung zu antikohärenten Spinzuständen, J. Phys. A: Mathe. Theor. 44, 342002 (2011).
https://doi.org/10.1088/1751-8113/44/34/342002

[38] M. Wang und Y. Zhu, Antikohärente Spin-2-Zustände und sphärische Designs, J. Phys. A: Mathe. Theor. 55, 425304 (2022).
https:///doi.org/10.1088/1751-8121/ac971d

[39] AZ Goldberg, AB Klimov, M.Grassl, G. Leuchs und LL Sánchez-Soto, Extremal Quantum States, AVS Quantum Sci. 2, 044701 (2020).
https: / / doi.org/ 10.1116 / 5.0025819

[40] AZ Goldberg, M. Grassl, G. Leuchs und LL Sánchez-Soto, Quantumness beyond entanglement: The case of symmetric states, Phys. Rev. A 105, 022433 (2022).
https: / / doi.org/ 10.1103 / PhysRevA.105.022433

[41] O. Giraud, P. Braun und D. Braun, Quantifying Quantumness and the quest for Queens of Quantum, New J. Phys. 12, 063005 (2010).
https://doi.org/10.1088/1367-2630/12/6/063005

[42] R. Delbourgo, Minimale Unsicherheitszustände für die Rotationsgruppe und verwandte Gruppen, J. Phys. A 10, L233 (1977).
https://doi.org/10.1088/0305-4470/10/11/012

[43] A. Wehrl, Zur Beziehung zwischen klassischer und quantenmechanischer Entropie, Rep. Math. Physik. 16, 353 (1979).
https://doi.org/10.1016/0034-4877(79)90070-3

[44] EH Lieb, Beweis einer Entropievermutung von Wehrl, Commun. Mathematik. Physik. 62, 35 (1978).
https: / / doi.org/ 10.1007 / BF01940328

[45] CT Lee, Wehrls Entropie der Spinzustände und Liebs Vermutung, J. Phys. A 21, 3749 (1988).
https://doi.org/10.1088/0305-4470/21/19/013

[46] EH Lieb und JP Solovej, Beweis einer Entropievermutung für Bloch-kohärente Spinzustände und ihre Verallgemeinerungen, Acta Math. 212, 379 (2014).
https://doi.org/10.1007/s11511-014-0113-6

[47] F. Bouchard, et al., Quantenmetrologie am Limit mit extremen Majorana-Konstellationen, Optica 4, 1429-1432 (2017).
https: / / doi.org/ 10.1364 / OPTICA.4.001429

[48] A. Wehrl, Allgemeine Eigenschaften der Entropie, Rev. Mod. Physik. 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[49] A. Wehrl, Die vielen Facetten der Entropie, Rep. Math. Physik. 30, 119 (1991).
https://doi.org/10.1016/0034-4877(91)90045-O

[50] S. Gnutzmann und K. Życzkowski, Renyi-Wehrl-Entropien als Maß für die Lokalisierung im Phasenraum, J. Phys. A 34, 10123 (2001).
https://doi.org/10.1088/0305-4470/34/47/317

[51] K. Życzkowski, Lokalisierung von Eigenzuständen und mittlerer Wehrl-Entropie, Physica E 9, 583 (2001).
https://doi.org/10.1016/S1386-9477(00)00266-6

[52] LL Sánchez-Soto, AB Klimov, P. de la Hoz und G. Leuchs, Quanten versus klassische Polarisationszustände: Wenn Multipole zählen, J. Phys. B 46 104011 (2013).
https://doi.org/10.1088/0953-4075/46/10/104011

[53] A. Tavakoli und N. Gisin, Die platonischen Körper und grundlegende Tests der Quantenmechanik, Quantum 4, 293 (2020).
https://doi.org/10.22331/q-2020-07-09-293

[54] H.Ch. Nguyen, S. Designolle, M. Barakat und O. Gühne, Symmetrien zwischen Messungen in der Quantenmechanik, Vorabdruck arXiv:2003.12553 (2022).
https:///doi.org/10.48550/arXiv.2003.12553
arXiv: 2003.12553

[55] JI Latorre und G. Sierra, Platonische Verschränkung, Quantum Inf. Berechnen. 21, 1081 (2021).
https: / / doi.org/ 10.26421 / QIC21.13-14-1

[56] K. Bolonek-Lasoń und P. Kosiński, Groups, Platonic solids and Bell inequalities, Quantum 5, 593 (2021).
https://doi.org/10.22331/q-2021-11-29-593

[57] KF Pál und T. Vértesi, Groups, Platonic Bell inequalities for all Dimensions, Quantum 6, 756 (2022).
https://doi.org/10.22331/q-2022-07-07-756

[58] RH Dicke, Kohärenz in spontanen Strahlungsprozessen, Phys. Rev. 93, 99 (1954).
https: / / doi.org/ 10.1103 / PhysRev.93.99

[59] V. Karimipour und L. Memarzadeh, Equientangled bases in Arbitrary Dimensions Phys. Rev. A 73, 012329 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.73.012329

[60] G. Rajchel, A. Gąsiorowski und K. Życzkowski, Robuste Hadamard-Matrizen, unistochastische Strahlen im Birkhoff-Polytop und gleichverschränkte Basen in zusammengesetzten Räumen Math. Komp. Wissenschaft. 12, 473 (2018).
https: / / doi.org/ 10.1007 / s11786-018-0384-y

[61] J. Czartowski, D. Goyeneche, M. Grassl und K. Życzkowski, Isoverschränkte gegenseitig erwartungsfreie Basen, symmetrische Quantenmessungen und Mixed-State-Designs, Phys. Rev. Lett. 124, 090503 (2020).
https://doi.org/ 10.1103/PhysRevLett.124.090503

[62] F. Del Santo, J. Czartowski, K. Życzkowski und N. Gisin, Iso-entangled bases and jointmeasures, Vorabdruck arXiv:2307.06998 (2023).
https:///doi.org/10.48550/arXiv.2307.06998
arXiv: 2307.06998

[63] R. Penrose, Über Bell-Nichtlokalität ohne Wahrscheinlichkeiten: einige seltsame Geometrie, Quantum Reflections (2000).

[64] J. Zimba und R. Penrose, Über Bell-Nichtlokalität ohne Wahrscheinlichkeiten: Mehr neugierige Geometrie, Stud. Hist. Phil. Wissenschaft. 24, 697 (1993).
https://doi.org/10.1016/0039-3681(93)90061-N

[65] JE Massad und PK Aravind, The Penrose dodecahedron revisited, Am. J. Physics 67, 631 (1999).
https: / / doi.org/ 10.1119 / 1.19336

[66] K. Husimi, Einige formale Eigenschaften der Dichtematrix, Proc. Physik. Mathematik. Soc. 22, 264 (1940).
https: / / doi.org/ 10.11429 / ppmsj1919.22.4_264

[67] W. Słomczyński und K. Życzkowski, Mittlere dynamische Entropie von Quantenkarten auf der Sphäre divergiert im semiklassischen Grenzwert, Phys. Rev. Lett. 80, 1880 (1998).
https://doi.org/ 10.1103/PhysRevLett.80.1880

[68] M. Piotrak, M. Kopciuch, AD Fard, M. Smolis, S. Pustelny, K. Korzekwa, Perfect Quantum Protractors, Preprint arXiv:2310.13045 (2023).
https:///doi.org/10.48550/arXiv.2310.13045
arXiv: 2310.13045

[69] NCN Maestro 7 2015/18/A/ST2/00274 Website https://chaos.if.uj.edu.pl/ karol/Maestro7/files/data3/Numerical_Results.dat.
https://chaos.if.uj.edu.pl/~karol/Maestro7/files/data3/Numerical_Results.dat

[70] D. Weingarten, Asymptotisches Verhalten von Gruppenintegralen im Grenzfall unendlichen Rangs, J. Math. Physik. 19, 999 (1978).
https: / / doi.org/ 10.1063 / 1.523807

[71] B. Collins und P. Śniady, Integration in Bezug auf das Haar-Maß für einheitliche, orthogonale und symplektische Gruppen, Commun. Mathematik. Physik. 264, 773 (2006).
https://doi.org/10.1007/s00220-006-1554-3

[72] G. Rajchel, Quantenkartierungen und -designs, Doktorarbeit, Vorabdruck arXiv:2204.13008 (2022).
https:///doi.org/10.48550/arXiv.2204.13008
arXiv: 2204.13008

[73] D. Martin und EP Wigner, Gruppentheorie und ihre Anwendung auf die Quantenmechanik atomarer Spektren, Academic Press Inc. NY (1959).
https://doi.org/10.1016/b978-0-12-750550-3.x5001-0

Zitiert von

[1] Michał Piotrak, Marek Kopciuch, Arash Dezhang Fard, Magdalena Smolis, Szymon Pustelny und Kamil Korzekwa, „Perfekte Quantenwinkelmesser“, arXiv: 2310.13045, (2023).

[2] Aaron Z. Goldberg, „Korrelationen für Teilmengen von Teilchen in symmetrischen Zuständen: Was Photonen in einem Lichtstrahl tun, wenn der Rest ignoriert wird“, arXiv: 2401.05484, (2024).

Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2024, 01:25:23 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.

On Der von Crossref zitierte Dienst Es wurden keine Daten zum Zitieren von Werken gefunden (letzter Versuch 2024-01-25 23:58:19).

Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.