„Richtige“ Verschiebungsregeln für Ableitungen gestört-parametrischer Quantenentwicklungen

„Richtige“ Verschiebungsregeln für Ableitungen gestört-parametrischer Quantenentwicklungen

Zeitstempel: 11. Juli 2023, 5:48 Uhr

Dirk Oliver Theis

Theoretische Informatik, Universität Tartu, Estland

Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.

Abstrakt

Banchi & Crooks (Quantum, 2021) haben Methoden zur Schätzung von Ableitungen von Erwartungswerten in Abhängigkeit von einem Parameter angegeben, der über eine sogenannte „gestörte“ Quantenentwicklung $xmapsto e^{i(x A + B)/hbar}$ eintritt. Ihre Methoden erfordern Modifikationen der angezeigten Unitarien, die über die bloße Änderung von Parametern hinausgehen. Darüber hinaus scheint für den Fall, dass der $B$-Term unvermeidbar ist, keine genaue Methode (unvoreingenommener Schätzer) für die Ableitung bekannt zu sein: Die Methode von Banchi & Crooks liefert eine Näherung.
In diesem Artikel stellen wir zum Schätzen der Ableitungen parametrisierter Erwartungswerte dieser Art eine Methode vor, die nur das Verschieben von Parametern und keine weiteren Modifikationen der Quantenentwicklungen erfordert (eine „richtige“ Verschiebungsregel). Unsere Methode ist exakt (dh sie liefert analytische Ableitungen und erwartungstreue Schätzer) und weist die gleiche Worst-Case-Varianz auf wie die von Banchi-Crooks.
Darüber hinaus diskutieren wir die Theorie rund um die richtigen Verschiebungsregeln, basierend auf der Fourier-Analyse gestörter parametrischer Quantenentwicklungen, was zu einer Charakterisierung der richtigen Verschiebungsregeln anhand ihrer Fourier-Transformationen führt, was uns wiederum zu Nichtexistenzergebnissen der richtigen führt Schichtregeln mit exponentieller Konzentration der Schichten. Wir leiten abgeschnittene Methoden ab, die Approximationsfehler aufweisen, und vergleichen sie mit denen von Banchi-Crooks auf der Grundlage vorläufiger numerischer Simulationen.

„Richtige“ Verschiebungsregeln für Ableitungen gestört-parametrischer Quantenentwicklungen PlatoBlockchain Data Intelligence. Vertikale Suche. Ai.

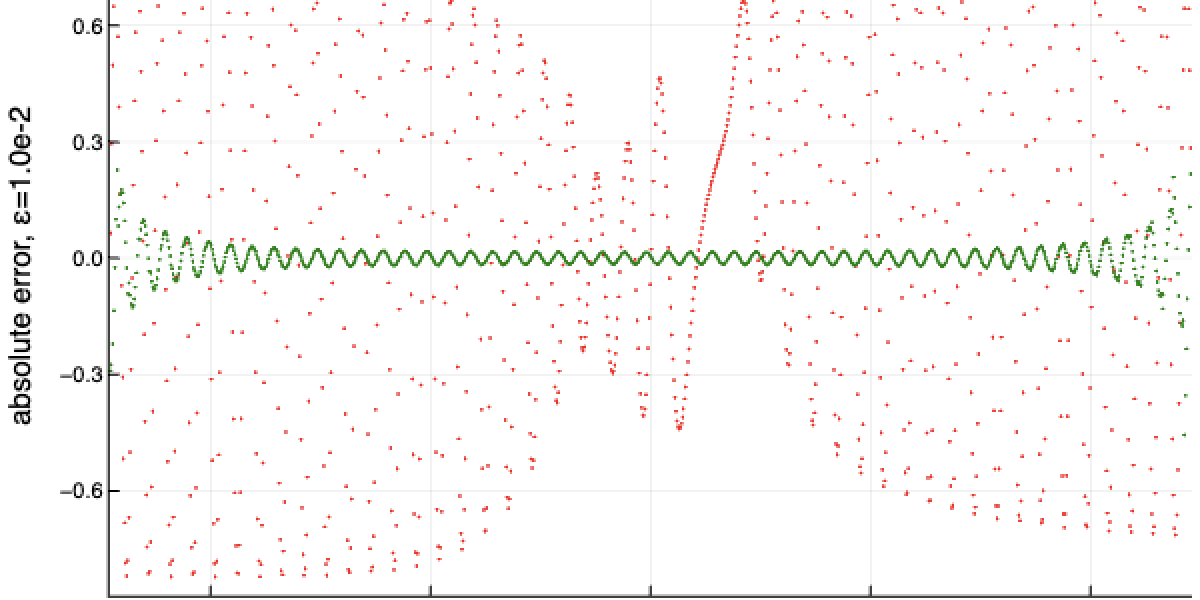
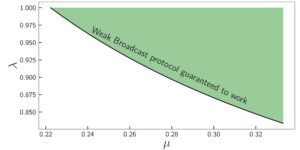
Ausgewähltes Bild: Vorläufige numerische Ergebnisse deuten darauf hin, dass die neue Methode besser ist als der Stand der Technik. Hier ist ein Diagramm, das für eine zufällig ausgewählte parametrisierte Quantenentwicklung den Fehler (Bias) bei der Schätzung der Ableitungen auf der Vertikalen und den Parameterwert auf der Horizontalen zeigt. Die grünen Punkte zeigen den Fehler der neuen Methode, die roten Punkte geben den Stand der Technik an. (Andere Leistungsvariablen sind für beide Methoden festgelegt und gleich.)

Populäre Zusammenfassung

Bei Versuchen, aktuelle oder in naher Zukunft befindliche Quantengeräte für sinnvolle Berechnungen zu nutzen, wird häufig der Variations-Hybrid-Quanten-Klassik-Ansatz verfolgt. Es besteht darin, die Quantenentwicklung zu parametrisieren und diese Parameter dann in einer Schleife zu optimieren, wobei zwischen Quanten- und klassischer Berechnung gewechselt wird.

Ein anderer Ansatz besteht darin, ein Rechenproblem auf einen Hamilton-Operator abzubilden, der auf Quantenhardware realisiert werden kann. Beispielsweise kann die Rydberg-Blockade zur Modellierung des Maximum Stable Set-Problems bei Quantengeräten mit kalten Atomen als Möglichkeit dienen, die Stabilitätsbeschränkungen teilweise zu realisieren.

Natürlich gibt es Versuche, die beiden Ansätze zu kombinieren.

Zur Optimierung der Parameter verwendet der Variationsansatz typischerweise Schätzer des Gradienten, und diese Schätzer sollten einen kleinen Bias und eine kleine Varianz aufweisen. In der Welt des digitalen Quantencomputings – also Quantenschaltungen mit (parametrisierten) Gates – ist die Schätzung der Gradienten gut verstanden und basiert auf sogenannten 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 𝑠ℎ𝑖𝑓𝑡 𝑟𝑢𝑙𝑒𝑠. Bei der Kombination des Digitalen mit dem Analogen entsteht jedoch die Situation, dass der parametrisierte Teil des Hamilton-Operators nicht mit anderen Teilen kommutiert.
Stellen Sie sich vor, Sie wählen als einen der Parameter die Rabi-Frequenz, beispielsweise lokal für ein einzelnes Atom, in einer Reihe von Rydberg-Atomen: Der Rabi-Term vertauscht sich nicht mit den Rydberg-Blockade-Termen. Es gibt noch viele weitere Beispiele. In solchen Situationen versagt die bekannte Schichtregeltheorie.
In unserer Arbeit schlagen wir eine neue Methode zur Schätzung von Derivaten für diese Situationen vor. Unsere Methode basiert auf dem bekannten Shift-Rule-Paradigma und verbessert den Stand der Technik bei der Reduzierung der Verzerrung des Schätzers.

► BibTeX-Daten

► Referenzen

[1] Jarrod R McClean, Nicholas C Rubin, Joonho Lee, Matthew P Harrigan, Thomas E O'Brien, Ryan Babbush, William J Huggins und Hsin-Yuan Huang. „Was uns die Grundlagen der Quanteninformatik über die Chemie lehren“. The Journal of Chemical Physics 155, 150901 (2021).
https://​/​doi.org/​10.48550/​arXiv.2106.03997

[2] Xiao Yuan, Suguru Endo, Qi Zhao, Ying Li und Simon C. Benjamin. „Theorie der Variationsquantensimulation“. Quantum 3, 191 (2019).
https://​/​doi.org/​10.48550/​arXiv.1812.08767

[3] Kosuke Mitarai, Makoto Negoro, Masahiro Kitagawa und Keisuke Fujii. „Quantenschaltungslernen“. Physik. Rev. A 98, 032309 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.032309

[4] Marcello Benedetti, Erika Lloyd, Stefan Sack und Mattia Fiorentini. „Parametrisierte Quantenschaltkreise als Modelle für maschinelles Lernen“. Quantenwissenschaft und -technologie 4, 043001 (2019).
https:/​/​doi.org/​10.1088/​2058-9565/​ab4eb5

[5] Edward Farhi, Jeffrey Goldstone und Sam Gutmann. „Ein Quantennäherungsoptimierungsalgorithmus“. Vorabdruck (2014).
https://​/​doi.org/​10.48550/​arXiv.1411.4028

[6] Eric R. Anschuetz, Jonathan P. Olson, Alán Aspuru-Guzik und Yudong Cao. „Variative Quantenfaktorisierung“. Vorabdruck (2018).
https://​/​doi.org/​10.48550/​arXiv.1808.08927

[7] Carlos Bravo-Prieto, Ryan LaRose, Marco Cerezo, Yigit Subasi, Lukasz Cincio und Patrick J Coles. „Variativer Quantenlinearlöser“. Vorabdruck (2019).
https://​/​doi.org/​10.48550/​arXiv.1909.05820

[8] Ryan Babbush und Hartmut Neven. „Training von Quantenentwicklungen mithilfe sublogischer Kontrollen“ (2019). US-Patent 10,275,717.

[9] Louis-Paul Henry, Slimane Thabet, Constantin Dalyac und Loïc Henriet. „Quantum Evolution Kernel: Maschinelles Lernen auf Graphen mit programmierbaren Arrays von Qubits“. Physical Review A 104, 032416 (2021).
https://​/​doi.org/​10.48550/​arXiv.2107.03247

[10] Constantin Dalyac, Loïc Henriet, Emmanuel Jeandel, Wolfgang Lechner, Simon Perdrix, Marc Porcheron und Margarita Veshchezerova. „Qualifizierung von Quantenansätzen für schwierige industrielle Optimierungsprobleme. eine Fallstudie im Bereich des intelligenten Ladens von Elektrofahrzeugen“. EPJ Quantentechnologie 8, 12 (2021).
https://​/​doi.org/​10.48550/​arXiv.2012.14859

[11] Ryan Sweke, Frederik Wilde, Johannes Meyer, Maria Schuld, Paul K. Fährmann, Barthélémy Meynard-Piganeau und Jens Eisert. „Stochastischer Gradientenabstieg für hybride quantenklassische Optimierung“. Quantum 4, 314 (2020).
https://​/​doi.org/​10.48550/​arXiv.1910.01155

[12] Jun Li, Xiaodong Yang, Xinhua Peng und Chang-Pu Sun. „Hybrider quantenklassischer Ansatz zur quantenoptimalen Steuerung“. Phys. Rev. Lett. 118, 150503 (2017).
https://doi.org/ 10.1103/PhysRevLett.118.150503

[13] Leonardo Banchi und Gavin E. Crooks. „Messung analytischer Gradienten der allgemeinen Quantenentwicklung mit der stochastischen Parameterverschiebungsregel“. Quantum 5, 386 (2021).
https:/​/​doi.org/​10.22331/​q-2021-01-25-386

[14] Richard P. Feynman. „Eine Operatorrechnung mit Anwendungen in der Quantenelektrodynamik“. Physical Review 84, 108 (1951).
https: / / doi.org/ 10.1103 / PhysRev.84.108

[15] Ralph M. Wilcox. „Exponentialoperatoren und Parameterdifferenzierung in der Quantenphysik“. Journal of Mathematical Physics 8, 962–982 (1967).
https: / / doi.org/ 10.1063 / 1.1705306

[16] Javier Gil Vidal und Dirk Oliver Theis. „Infinitesimalrechnung auf parametrisierten Quantenschaltungen“. Vorabdruck (2018).
https://​/​doi.org/​10.48550/​arXiv.1812.06323

[17] David Wierichs, Josh Izaac, Cody Wang und Cedric Yen-Yu Lin. „Allgemeine Parameterverschiebungsregeln für Quantengradienten“. Vorabdruck (2021).
https://​/​doi.org/​10.48550/​arXiv.2107.12390

[18] Dirk Oliver Theis. „Optimalität endlich unterstützter Parameterverschiebungsregeln für Ableitungen von Variationsquantenschaltungen“. Vorabdruck (2021).
https://​/​doi.org/​10.48550/​arXiv.2112.14669

[19] Michael Reed und Barry Simon. „Methoden der modernen mathematischen Physik II: Fourier-Analyse, Selbstadjungiertheit“. Band 2. Akademische Presse. (1975).

[20] Jarrod R. McClean, Sergio Boixo, Vadim N. Smelyanskiy, Ryan Babbush und Hartmut Neven. „Unfruchtbare Hochebenen in Trainingslandschaften für Quanten-Neuronale Netze“. Naturkommunikation 9, 4812 (2018).
https:/​/​doi.org/​10.1038/​s41467-018-07090-4

[21] Andrew Arrasmith, Zoë Holmes, Marco Cerezo und Patrick J. Coles. „Äquivalenz von quantenkargen Hochebenen zu Kostenkonzentration und engen Schluchten“. Quantenwissenschaft und -technologie 7, 045015 (2022).
https://​/​doi.org/​10.48550/​arXiv.2104.05868

[22] Walter Rudin. „Funktionsanalyse“. McGraw-Hill. (1991).

[23] Elias M. Stein und Rami Shakarchi. „Fourier-Analyse: Eine Einführung“. Band 1. Princeton University Press. (2011).

[24] Gerald B. Folland. „Ein Kurs in abstrakter harmonischer Analyse“. Band 29. CRC-Presse. (2016).

[25] Don Zagier. „Die Dilogarithmusfunktion“. In Grenzen in Zahlentheorie, Physik und Geometrie II. Seiten 3–65. Springer (2007).

[26] Leonard C. Maximon. „Die Dilogarithmusfunktion für komplexe Argumente“. Tagungsband der Royal Society of London. Reihe A: Mathematische, physikalische und technische Wissenschaften 459, 2807–2819 (2003).
https: / / doi.org/ 10.1098 / rspa.2003.1156

[27] Elias M. Stein und Rami Shakarchi. „Komplexe Analyse“. Band 2. Princeton University Press. (2010).

[28] Walter Rudin. „Reale und komplexe Analyse“. McGraw-Hill. (1987).

[29] Heinz Bauer. „Massen- und Integrationstheorie“. Walter de Gruyter. (1992). 2. Auflage.

[30] Franz Rellich und Joseph Berkowitz. „Störungstheorie von Eigenwertproblemen“. CRC-Presse. (1969).

Zitiert von

[1] Roeland Wiersema, Dylan Lewis, David Wierichs, Juan Carrasquilla und Nathan Killoran, „Hier kommt das $mathrm{SU}(N)$: multivariate Quantengatter und Gradienten“, arXiv: 2303.11355, (2023).

Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2023, 07:14:10 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.

On Der von Crossref zitierte Dienst Es wurden keine Daten zum Zitieren von Werken gefunden (letzter Versuch 2023-07-14 10:03:04).

Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.

Zeitstempel:

Mehr von Quantenjournal