1Goldman, Sachs & Co., New York, NY
2IBM Quantum, IBM Research - Zürich
Findest du dieses Paper interessant oder möchtest du darüber diskutieren? Scite oder hinterlasse einen Kommentar zu SciRate.
Abstrakt
Wir führen einen Quantenalgorithmus ein, um das Marktrisiko von Finanzderivaten zu berechnen. Frühere Arbeiten haben gezeigt, dass die Quantenamplitudenschätzung die Preisgestaltung von Derivaten im Zielfehler quadratisch beschleunigen kann, und wir erweitern dies auf einen quadratischen Fehlerskalierungsvorteil bei der Marktrisikoberechnung. Wir zeigen, dass der Einsatz von Quantengradienten-Schätzalgorithmen einen weiteren quadratischen Vorteil in der Anzahl der damit verbundenen Marktsensitivitäten liefern kann, die üblicherweise als $greeks$ bezeichnet werden. Durch die numerische Simulation der Quantengradienten-Schätzalgorithmen für Finanzderivate von praktischem Interesse zeigen wir, dass wir nicht nur die Griechen in den untersuchten Beispielen erfolgreich schätzen können, sondern dass der Ressourcenbedarf in der Praxis erheblich geringer sein kann als durch theoretische Komplexitätsgrenzen erwartet . Dieser zusätzliche Vorteil bei der Berechnung des Finanzmarktrisikos senkt die geschätzte logische Taktrate, die für den finanziellen Quantenvorteil von Chakrabarti et al. erforderlich ist. [Quantum 5, 463 (2021)] um einen Faktor von ~7, von 50 MHz auf 7 MHz, selbst für eine bescheidene Anzahl von Griechen nach Industriestandards (vier). Darüber hinaus zeigen wir, dass der Quantenalgorithmus über 60 QPUs parallelisiert werden kann, wenn wir Zugriff auf genügend Ressourcen haben. In diesem Fall würde die logische Taktrate jedes Geräts, die erforderlich ist, um die gleiche Gesamtlaufzeit wie die serielle Ausführung zu erreichen, ~100 kHz betragen. In dieser Arbeit fassen und vergleichen wir verschiedene Kombinationen von Quanten- und klassischen Ansätzen, die zur Berechnung des Marktrisikos von Finanzderivaten verwendet werden könnten.
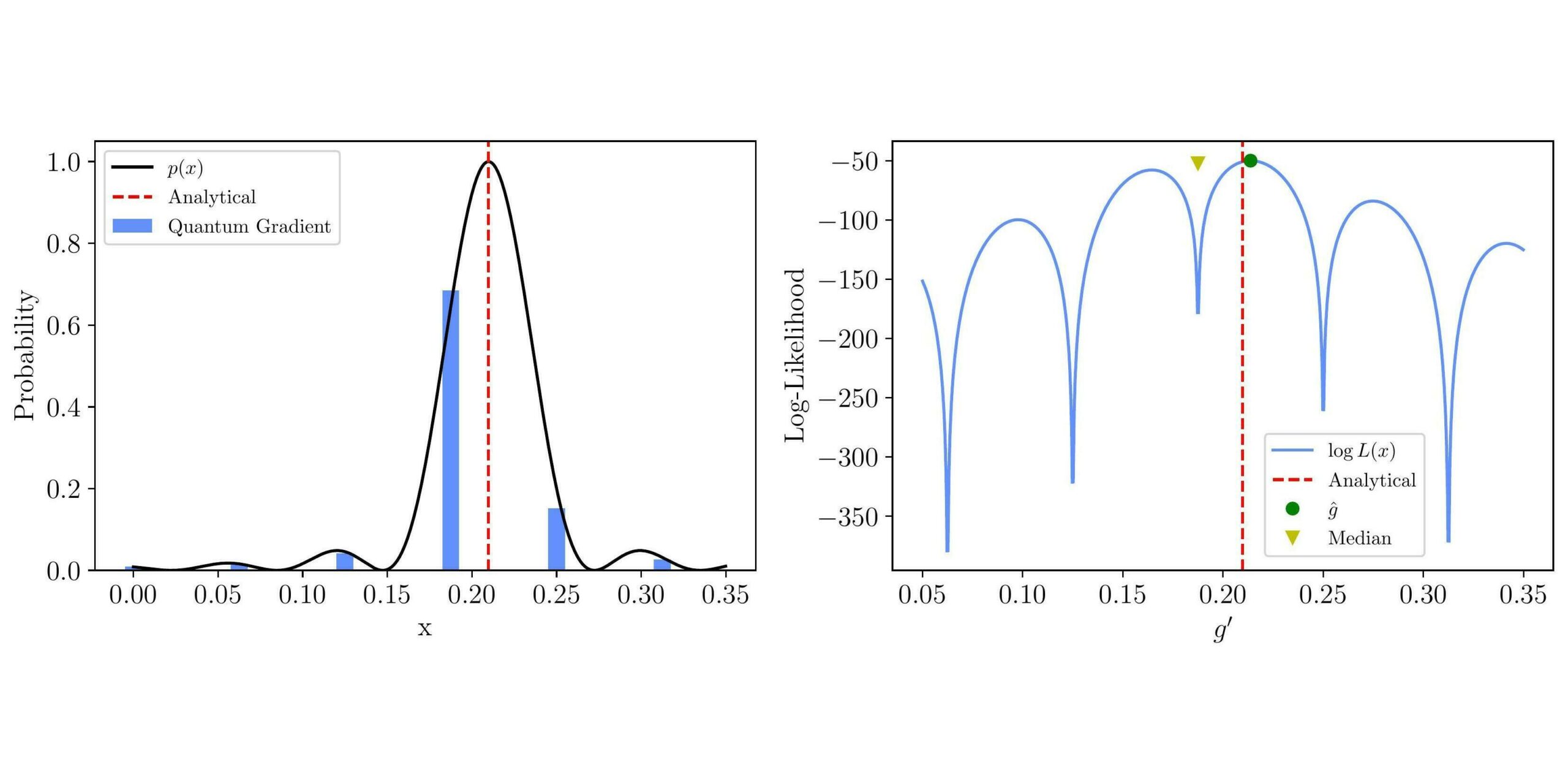
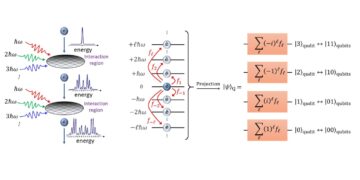
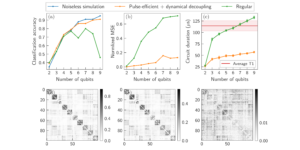
Ausgewähltes Bild: Die Maximum-Likelihood-Schätzung kann in Verbindung mit Quantengradientenalgorithmen verwendet werden, um bessere Gradientenschätzungen zu erhalten. Links: Die diskrete Wahrscheinlichkeitsverteilung vor der Messung des Vega-Griechischen $partialtheta/partialsigma$ für eine Korboption (blaue Balken) wird an die erwartete Verteilung (schwarze Linie) angepasst. Rechts: Das globale Maximum der Log-Wahrscheinlichkeit (grüner Punkt) gibt uns eine bessere Schätzung des wahren Werts (gestrichelte rote Linie) als das wahrscheinlichste Ergebnis, wenn wir aus der Wahrscheinlichkeitsverteilung eine Stichprobe ziehen und den Median nehmen (gelbes Dreieck).
Populäre Zusammenfassung
Eine verwandte und wichtige Finanzanwendung ist die Berechnung der Sensitivität von Derivatepreisen gegenüber Modell- und Marktparametern. Dies läuft auf die Berechnung von Gradienten des Derivatpreises in Bezug auf Eingabeparameter hinaus. Eine primäre geschäftliche Verwendung zur Berechnung dieser Gradienten besteht darin, eine Absicherung des Marktrisikos zu ermöglichen, das sich aus dem Engagement in Derivatekontrakten ergibt. Die Absicherung dieses Risikos ist für Finanzunternehmen von entscheidender Bedeutung. Gradienten von Finanzderivaten werden typischerweise als Griechisch bezeichnet, da diese Mengen üblicherweise mit griechischen Buchstaben bezeichnet werden.
In dieser Arbeit untersuchen wir die Wirksamkeit von Quantengradientenalgorithmen bei der Schätzung von Griechen in einem Quantensetting. Wir stellen eine Methode vor, die Gradientenalgorithmen und Maximum-Likelihood-Schätzung (MLE) kombiniert, um die Griechen einer pfadabhängigen Korboption zu schätzen, und zeigen, dass ein Quantenvorteil zur Berechnung des Risikos mit Quantencomputern erreichbar sein kann, deren Taktraten 7-mal langsamer sind als erforderlich die Preisgestaltung selbst, was auf einen weiteren möglichen Weg für Quantenvorteile im Finanzwesen hinweist.
► BibTeX-Daten
► Referenzen
[1] P. Rebentrost, B. Gupt und TR Bromley, „Quantum Computational Finance: Monte Carlo Pricing of Financial Derivatives“, Phys. Rev. A 98, 022321 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.98.022321
[2] S. Woerner und DJ Egger, "Quantenrisikoanalyse", npj Quantum Information 5 (2019), 10.1038 / s41534-019-0130-6.
https://doi.org/10.1038/s41534-019-0130-6
[3] DJ Egger, RG Gutierrez, JC Mestre und S. Woerner, „Kreditrisikoanalyse mit Quantencomputern“, IEEE Transactions on Computers (2020), 10.1109/TC.2020.3038063.
https: / / doi.org/ 10.1109 / TC.2020.3038063
[4] N. Stamatopoulos, DJ Egger, Y. Sun, C. Zoufal, R. Iten, N. Shen und S. Woerner, „Option pricing using Quantencomputer“, Quantum 4, 291 (2020).
https://doi.org/10.22331/q-2020-07-06-291
[5] S. Chakrabarti, R. Krishnakumar, G. Mazzola, N. Stamatopoulos, S. Woerner und WJ Zeng, „Eine Schwelle für Quantenvorteile bei der Preisgestaltung von Derivaten“, Quantum 5, 463 (2021).
https://doi.org/10.22331/q-2021-06-01-463
[6] A. Montanaro, „Quantenbeschleunigung von Monte-Carlo-Methoden“, Verfahren der Royal Society of London A: Mathematische, Physikalische und Ingenieurwissenschaften 471 (2015), 10.1098 / rspa.2015.0301.
https: / / doi.org/ 10.1098 / rspa.2015.0301
[7] J. Hull, Optionen, Futures und andere Derivate, 6. Aufl. (Pearson Prentice Hall, Upper Saddle River, NJ [ua], 2006).
https://doi.org/10.1007/978-1-4419-9230-7_2
[8] A. Gilyén, S. Arunachalam und N. Wiebe, „Optimierung von Quantenoptimierungsalgorithmen durch schnellere Quantengradientenberechnung“, Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, 1425–1444 (2019).
https: / / doi.org/ 10.1137 / 1.9781611975482.87
[9] SP Jordan, „Schneller Quantenalgorithmus zur numerischen Gradientenschätzung“, Physical Review Letters 95 (2005), 10.1103/physrevlett.95.050501.
https://doi.org/ 10.1103/physrevlett.95.050501
[10] S. Chakrabarti, AM Childs, T. Li und X. Wu, „Quantenalgorithmen und untere Grenzen für die konvexe Optimierung“, Quantum 4, 221 (2020).
https://doi.org/10.22331/q-2020-01-13-221
[11] G. Brassard, P. Hoyer, M. Mosca und A. Tapp, "Quantum Amplitude Amplification and Estimation", Contemporary Mathematics 305 (2002), 10.1090 / conm / 305/05215.
https: / / doi.org/ 10.1090 / conm / 305/05215
[12] P. Glasserman und D. Yao, „Einige Richtlinien und Garantien für gemeinsame Zufallszahlen“, Management Science 38, 884 (1992).
https: / / doi.org/ 10.1287 / mnsc.38.6.884
[13] B. Fornberg, „Erzeugung von Finite-Differenzen-Formeln auf willkürlich beabstandeten Gittern“, Mathematics of Computation 51, 699 (1988).
https://doi.org/10.1090/S0025-5718-1988-0935077-0
[14] M. Gevrey, „Sur la nature analytique des solutions des équations aux dérivées partielles. premier mémoire“, Annales scientifiques de l'École Normale Supérieure 3e série, 35, 129 (1918).
https:///doi.org/10.24033/asens.706
[15] GH Low und IL Chuang, „Hamiltonian simulation by qubitization“, Quantum 3, 163 (2019).
https://doi.org/10.22331/q-2019-07-12-163
[16] A. Gilyén, Y. Su, GH Low und N. Wiebe, „Quantum Singular Value Transformation and Beyond: Exponential Improvements for Quantum Matrix Arithmetics“, in Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing (2019) S. 193–204.
https: / / doi.org/ 10.1145 / 3313276.3316366
[17] JM Martyn, Y. Liu, ZE Chin und IL Chuang, „Efficient Fully-Coherent Hamiltonian Simulation“, (2021), 10.48550/arXiv.2110.11327.
https:///doi.org/10.48550/arXiv.2110.11327
[18] F. Black und M. Scholes, "Die Preisgestaltung von Optionen und Unternehmensverbindlichkeiten", Journal of Political Economy 81, 637 (1973).
https: / / doi.org/ 10.1086 / 260062
[19] Y. Suzuki, S. Uno, R. Raymond, T. Tanaka, T. Onodera und N. Yamamoto, "Amplitudenschätzung ohne Phasenschätzung", Quantum Information Processing 19, 75 (2020).
https://doi.org/10.1007/s11128-019-2565-2
[20] T. Tanaka, Y. Suzuki, S. Uno, R. Raymond, T. Onodera und N. Yamamoto, „Amplitudenschätzung über maximale Wahrscheinlichkeit auf verrauschten Quantencomputern“, Quantum Information Processing 20, 293 (2021).
https://doi.org/10.1007/s11128-021-03215-9
[21] D. Grinko, J. Gacon, C. Zoufal und S. Woerner, „Iterative Quantenamplitudenschätzung“, npj Quantum Information 7 (2021), 10.1038/s41534-021-00379-1.
https://doi.org/10.1038/s41534-021-00379-1
[22] K.-R. Koch, Parameterschätzung und Hypothesentest in linearen Modellen (Springer-Verlag Berlin Heidelberg, 1999).
https://doi.org/10.1007/978-3-662-03976-2
[23] AG Fowler und C. Gidney, „Low Overhead Quantum Computation Using Lattice Surgery“, (2019), 10.48550/arXiv.1808.06709.
https:///doi.org/10.48550/arXiv.1808.06709
[24] C. Homescu, „Adjoints and Automatic (Algorithmic) Differentiation in Computational Finance“, Risk Management eJournal (2011), 10.2139/ssrn.1828503.
https: / / doi.org/ 10.2139 / ssrn.1828503
[25] G. Pages, O. Pironneau und G. Sall, „Vibrato und automatische Differenzierung für Derivate hoher Ordnung und Sensitivitäten von Finanzoptionen“, Journal of Computational Finance 22 (2016), 10.21314/JCF.2018.350.
https:///doi.org/10.21314/JCF.2018.350
[26] L. Capriotti, „Schnelle Griechen durch algorithmische Differenzierung“, J. Comput. Finanzen 14 (2010), 10.2139/ssrn.1619626.
https: / / doi.org/ 10.2139 / ssrn.1619626
[27] L. Capriotti und M. Giles, „Schnelle Korrelationsgriechen durch adjoint algorithmische Differenzierung“, ERN: Simulation Methods (Thema) (2010), 10.2139/ssrn.1587822.
https: / / doi.org/ 10.2139 / ssrn.1587822
[28] CH Bennett, „Logical Reversibility of Computation“, IBM Journal of Research and Development 17 (1973), 10.1147/rd.176.0525.
https: / / doi.org/ 10.1147 / rd.176.0525
Zitiert von
[1] AK Fedorov, N. Gisin, SM Beloussov und AI Lvovsky, „Quantum Computing at the Quantum Advantage Threshold: a Down-to-Business Review“, arXiv: 2203.17181.
[2] Peter D. Johnson, Alexander A. Kunitsa, Jérôme F. Gonthier, Maxwell D. Radin, Corneliu Buda, Eric J. Doskocil, Clena M. Abuan und Jhonathan Romero, „Reduktion der Kosten der Energieschätzung in der Variation Quanten-Eigensolver-Algorithmus mit robuster Amplitudenschätzung“, arXiv: 2203.07275.
[3] Gabriele Agliardi, Michele Grossi, Mathieu Pellen und Enrico Prati, „Quantenintegration von Elementarteilchenprozessen“, Physikbriefe B 832, 137228 (2022).
[4] João F. Doriguello, Alessandro Luongo, Jinge Bao, Patrick Rebentrost und Miklos Santha, „Quantenalgorithmus für stochastische optimale Stoppprobleme mit Anwendungen im Finanzwesen“, arXiv: 2111.15332.
[5] Hao Tang, Wenxun Wu und Xian-Min Jin, „Quantum Computation for Pricing Caps using the LIBOR Market Model“, arXiv: 2207.01558.
Die obigen Zitate stammen von SAO / NASA ADS (Zuletzt erfolgreich aktualisiert am 2022, 07:20:16 Uhr). Die Liste ist möglicherweise unvollständig, da nicht alle Verlage geeignete und vollständige Zitationsdaten bereitstellen.
Konnte nicht abrufen Crossref zitiert von Daten während des letzten Versuchs 2022-07-20 16:45:46: Von Crossref konnten keine zitierten Daten für 10.22331 / q-2022-07-20-770 abgerufen werden. Dies ist normal, wenn der DOI kürzlich registriert wurde.
Dieses Papier ist in Quantum unter dem veröffentlicht Creative Commons Namensnennung 4.0 International (CC BY 4.0) Lizenz. Das Copyright verbleibt bei den ursprünglichen Copyright-Inhabern wie den Autoren oder deren Institutionen.