Οριστικός οδηγός για ομαδοποίηση K-Means με το Scikit-Learn

Εισαγωγή

Ομαδοποίηση K-Means είναι ένας από τους πιο ευρέως χρησιμοποιούμενους αλγόριθμους μη εποπτευόμενης μηχανικής μάθησης που σχηματίζουν συμπλέγματα δεδομένων με βάση την ομοιότητα μεταξύ παρουσιών δεδομένων.

Σε αυτόν τον οδηγό, θα ρίξουμε πρώτα μια ματιά σε ένα απλό παράδειγμα για να κατανοήσουμε πώς λειτουργεί ο αλγόριθμος K-Means πριν τον εφαρμόσουμε χρησιμοποιώντας το Scikit-Learn. Στη συνέχεια, θα συζητήσουμε πώς να προσδιορίσουμε τον αριθμό των συμπλεγμάτων (Ks) στο K-Means και επίσης θα καλύψουμε μετρήσεις απόστασης, διακύμανση και K-Means πλεονεκτήματα και μειονεκτήματα.

Κινητοποίηση

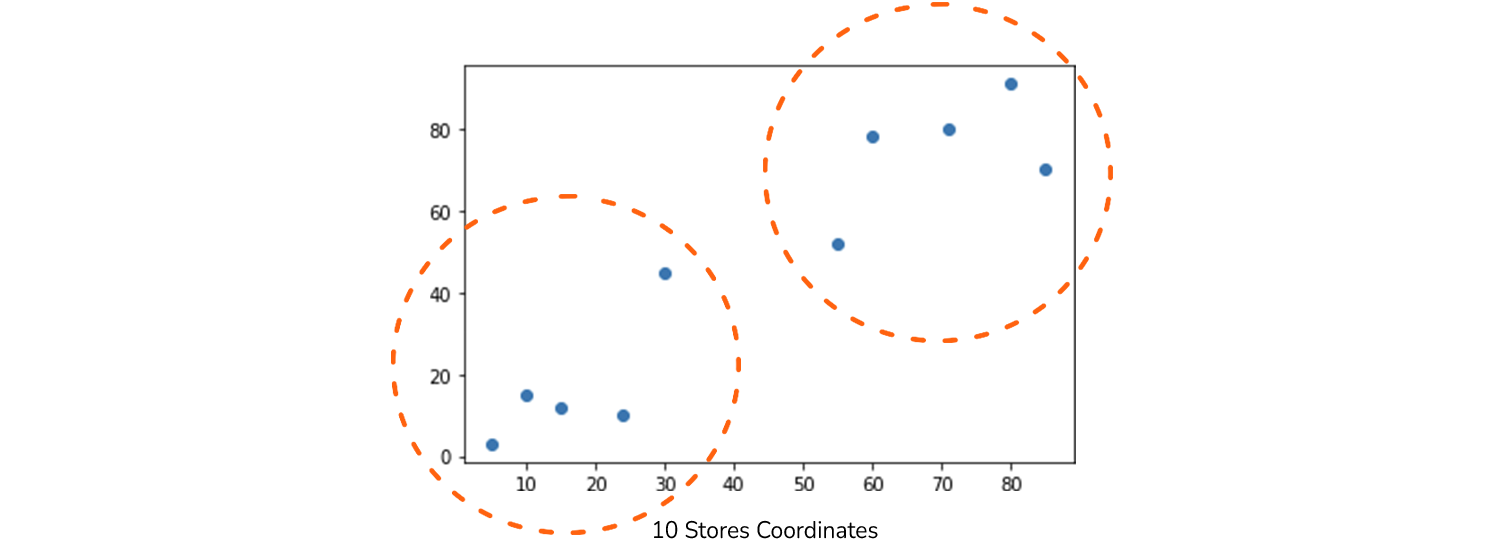
Φανταστείτε την παρακάτω κατάσταση. Μια μέρα, περπατώντας στη γειτονιά, παρατήρησες ότι υπήρχαν 10 ψιλικατζίδικα και άρχισες να αναρωτιέσαι ποια καταστήματα ήταν παρόμοια – πιο κοντά το ένα στο άλλο σε κοντινή απόσταση. Κατά την αναζήτηση τρόπων απάντησης σε αυτήν την ερώτηση, συναντήσατε μια ενδιαφέρουσα προσέγγιση που χωρίζει τα καταστήματα σε ομάδες με βάση τις συντεταγμένες τους σε έναν χάρτη.

Για παράδειγμα, αν ένα κατάστημα βρισκόταν 5 χλμ δυτικά και 3 χλμ βόρεια - θα το εκχωρούσατε (5, 3) συντεταγμένες σε αυτό, και να το αναπαραστήσουν σε ένα γράφημα. Ας σχεδιάσουμε αυτό το πρώτο σημείο για να οπτικοποιήσουμε τι συμβαίνει:

import matplotlib.pyplot as plt

plt.title("Store With Coordinates (5, 3)")
plt.scatter(x=5, y=3)

Αυτό είναι μόνο το πρώτο σημείο, ώστε να έχουμε μια ιδέα για το πώς μπορούμε να εκπροσωπήσουμε ένα κατάστημα. Ας υποθέσουμε ότι έχουμε ήδη 10 συντεταγμένες στα 10 καταστήματα που συγκεντρώθηκαν. Αφού τα οργάνωσε σε α numpy πίνακα, μπορούμε επίσης να σχεδιάσουμε τις τοποθεσίες τους:

import numpy as np

points = np.array([[5, 3], [10, 15], [15, 12], [24, 10], [30, 45], [85, 70], [71, 80], [60, 78], [55, 52],[80, 91]])

xs = points[:,0] 
ys = points[:,1]  

plt.title("10 Stores Coordinates")
plt.scatter(x=xs, y=ys)

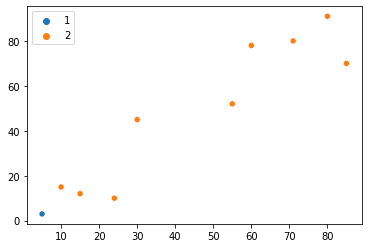
Πώς να εφαρμόσετε με μη αυτόματο τρόπο τον αλγόριθμο K-Means

Τώρα μπορούμε να δούμε τα 10 καταστήματα σε ένα γράφημα και το κύριο πρόβλημα είναι να βρούμε υπάρχει τρόπος να χωριστούν σε διαφορετικές ομάδες με βάση την εγγύτητα; Απλά ρίχνοντας μια γρήγορη ματιά στο γράφημα, πιθανότατα θα παρατηρήσουμε δύο ομάδες καταστημάτων – το ένα είναι τα κάτω σημεία προς τα κάτω αριστερά και το άλλο είναι τα πάνω δεξιά σημεία. Ίσως, μπορούμε ακόμη και να διαφοροποιήσουμε αυτά τα δύο σημεία στη μέση ως ξεχωριστή ομάδα – επομένως δημιουργώντας τρεις διαφορετικές ομάδες.

Σε αυτήν την ενότητα, θα εξετάσουμε τη διαδικασία της μη αυτόματης ομαδοποίησης σημείων – χωρίζοντάς τα στον δεδομένο αριθμό ομάδων. Με αυτόν τον τρόπο, ουσιαστικά θα προχωρήσουμε προσεκτικά σε όλα τα βήματα του K-Means αλγόριθμος ομαδοποίησης. Μέχρι το τέλος αυτής της ενότητας, θα αποκτήσετε τόσο διαισθητική όσο και πρακτική κατανόηση όλων των βημάτων που εκτελούνται κατά τη διάρκεια της ομαδοποίησης K-Means. Μετά από αυτό, θα το αναθέσουμε στο Scikit-Learn.

Ποιος θα ήταν ο καλύτερος τρόπος για να προσδιορίσετε εάν υπάρχουν δύο ή τρεις ομάδες βαθμών; Ένας απλός τρόπος θα ήταν να επιλέξετε απλώς έναν αριθμό ομάδων – για παράδειγμα, δύο – και στη συνέχεια να προσπαθήσετε να ομαδοποιήσετε σημεία με βάση αυτή την επιλογή.

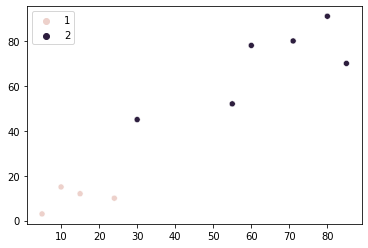
Ας πούμε ότι έχουμε αποφασίσει ότι υπάρχουν δύο ομάδες των καταστημάτων μας (πόντους). Τώρα, πρέπει να βρούμε έναν τρόπο να καταλάβουμε ποια σημεία ανήκουν σε ποια ομάδα. Αυτό θα μπορούσε να γίνει επιλέγοντας ένα σημείο για αντιπροσώπευση ομάδα 1 και ένα να εκπροσωπεί ομάδα 2. Αυτά τα σημεία θα χρησιμοποιηθούν ως αναφορά κατά τη μέτρηση της απόστασης από όλα τα άλλα σημεία σε κάθε ομάδα.

Με αυτόν τον τρόπο, πείτε το σημείο (5, 3) καταλήγει να ανήκει στην ομάδα 1, και σημείο (79, 60) στην ομάδα 2. Όταν προσπαθείτε να εκχωρήσετε ένα νέο σημείο (6, 3) σε ομάδες, πρέπει να μετρήσουμε την απόστασή του από αυτά τα δύο σημεία. Στην περίπτωση του σημείου (6, 3) is πιο κοντά στο (5, 3), επομένως ανήκει στην ομάδα που αντιπροσωπεύεται από αυτό το σημείο – ομάδα 1. Με αυτόν τον τρόπο, μπορούμε εύκολα να ομαδοποιήσουμε όλα τα σημεία σε αντίστοιχες ομάδες.

Σε αυτό το παράδειγμα, εκτός από τον προσδιορισμό του αριθμού των ομάδων (συστάδες) – επιλέγουμε επίσης κάποια σημεία για να είναι α αναφορά της απόστασης για νέους βαθμούς κάθε ομάδας.

Αυτή είναι η γενική ιδέα για να κατανοήσουμε τις ομοιότητες μεταξύ των καταστημάτων μας. Ας το κάνουμε πράξη – μπορούμε πρώτα να επιλέξουμε τα δύο σημεία αναφοράς στα τυχαίος. Το σημείο αναφοράς του ομάδα 1 θα είναι (5, 3) και το σημείο αναφοράς του ομάδα 2 θα είναι (10, 15). Μπορούμε να επιλέξουμε και τα δύο σημεία μας numpy συστοιχία από [0] και [1] ευρετήρια και αποθηκεύστε τα σε g1 (ομάδα 1) και g2 (ομάδα 2) μεταβλητές:

g1 = points[0]
g2 = points[1]

Αφού το κάνουμε αυτό, πρέπει να υπολογίσουμε την απόσταση από όλα τα άλλα σημεία σε αυτά τα σημεία αναφοράς. Αυτό εγείρει ένα σημαντικό ερώτημα - πώς να μετρήσετε αυτή την απόσταση. Μπορούμε ουσιαστικά να χρησιμοποιήσουμε οποιοδήποτε μέτρο απόστασης, αλλά, για τους σκοπούς αυτού του οδηγού, ας χρησιμοποιήσουμε την Ευκλείδεια Απόσταση_.

Μπορεί να είναι χρήσιμο να γνωρίζουμε ότι το μέτρο της Ευκλείδειας απόστασης βασίζεται στο θεώρημα του Πυθαγόρα:

$$
c^2 = a^2 + b^2
$$

Όταν προσαρμόζεται σε σημεία σε ένα επίπεδο - (a1, b1) και (a2, b2), ο προηγούμενος τύπος γίνεται:

$$
c^2 = (a2-a1)^2 + (b2-b1)^2
$$

Η απόσταση θα είναι η τετραγωνική ρίζα του c, οπότε μπορούμε να γράψουμε και τον τύπο ως:

$$
ευκλείδειος_{dist} = sqrt[2][(a2 – a1)^2 + (b2 – b1) ^2)]
$$

Μέχρι στιγμής, έχουμε επιλέξει τα σημεία για να αναπαραστήσουμε ομάδες και ξέρουμε πώς να υπολογίζουμε τις αποστάσεις. Τώρα, ας βάλουμε τις αποστάσεις και τις ομάδες μαζί, εκχωρώντας κάθε έναν από τους συλλεγμένους πόντους καταστήματος σε μια ομάδα.

Για να το οπτικοποιήσουμε καλύτερα αυτό, θα δηλώσουμε τρεις λίστες. Ο πρώτος που αποθηκεύει σημεία της πρώτης ομάδας – points_in_g1. Το δεύτερο που αποθηκεύει πόντους από την ομάδα 2 – points_in_g2και το τελευταίο - group, Με επιγραφή τα σημεία ως είτε 1 (ανήκει στην ομάδα 1) ή 2 (ανήκει στην ομάδα 2):

points_in_g1 = []
points_in_g2 = []
group = []

Μπορούμε τώρα να επαναλάβουμε τα σημεία μας και να υπολογίσουμε την Ευκλείδεια απόσταση μεταξύ τους και κάθε αναφοράς της ομάδας μας. Κάθε σημείο θα είναι πιο κοντά σε μία από τις δύο ομάδες – ανάλογα με το ποια ομάδα είναι πιο κοντά, θα αντιστοιχίσουμε κάθε σημείο στην αντίστοιχη λίστα, προσθέτοντας επίσης 1 or 2 στο group λίστα:

for p in points:
    x1, y1 = p[0], p[1]
    euclidean_distance_g1 = np.sqrt((g1[0] - x1)**2 + (g1[1] - y1)**2)
    euclidean_distance_g2 = np.sqrt((g2[0] - x1)**2 + (g2[1] - y1)**2)
    if euclidean_distance_g1 < euclidean_distance_g2:
        points_in_g1.append(p)
        group.append('1')
    else:
        points_in_g2.append(p)
        group.append('2')

Ας δούμε τα αποτελέσματα αυτής της επανάληψης για να δούμε τι συνέβη:

print(f'points_in_g1:{points_in_g1}n 
npoints_in_g2:{points_in_g2}n 
ngroup:{group}')

Το οποίο έχει ως αποτέλεσμα:

points_in_g1:[array([5, 3])]
 
points_in_g2:[array([10, 15]), array([15, 12]), 
              array([24, 10]), array([30, 45]), 
              array([85, 70]), array([71, 80]),
              array([60, 78]), array([55, 52]), 
              array([80, 91])]
 
group:[1, 2, 2, 2, 2, 2, 2, 2, 2, 2] 

Μπορούμε επίσης να σχεδιάσουμε το αποτέλεσμα της ομαδοποίησης, με διαφορετικά χρώματα με βάση τις εκχωρημένες ομάδες, χρησιμοποιώντας το Seaborn's scatterplot() με group ως hue διαφωνία:

import seaborn as sns

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

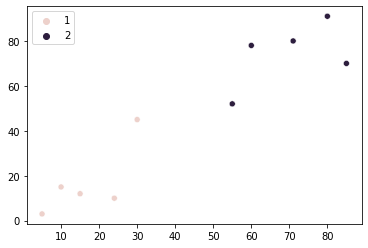
Είναι ξεκάθαρα ορατό ότι μόνο ο πρώτος μας βαθμός εκχωρήθηκε στην ομάδα 1, και όλοι οι άλλοι βαθμοί ανατέθηκαν στην ομάδα 2. Αυτό το αποτέλεσμα διαφέρει από αυτό που είχαμε οραματιστεί στην αρχή. Λαμβάνοντας υπόψη τη διαφορά μεταξύ των αποτελεσμάτων μας και των αρχικών μας προσδοκιών – υπάρχει τρόπος να το αλλάξουμε αυτό; Φαίνεται ότι υπάρχει!

Μια προσέγγιση είναι να επαναλάβετε τη διαδικασία και να επιλέξετε διαφορετικά σημεία ως αναφορές των ομάδων. Αυτό θα αλλάξει τα αποτελέσματά μας, ελπίζουμε, περισσότερο σε ευθυγράμμιση με αυτό που είχαμε οραματιστεί στην αρχή. Αυτή τη δεύτερη φορά, μπορούσαμε να τα επιλέξουμε όχι τυχαία όπως κάναμε προηγουμένως, αλλά παίρνοντας ένα εννοώ όλων των ήδη ομαδοποιημένων σημείων μας. Με αυτόν τον τρόπο, αυτά τα νέα σημεία θα μπορούσαν να τοποθετηθούν στη μέση των αντίστοιχων ομάδων.

Για παράδειγμα, αν η δεύτερη ομάδα είχε μόνο βαθμούς (10, 15), (30, 45). Το νέο κεντρικός σημείο θα ήταν (10 + 30)/2 και (15+45)/2 – που ισούται με (20, 30).

Εφόσον έχουμε βάλει τα αποτελέσματά μας σε λίστες, μπορούμε να τα μετατρέψουμε πρώτα σε numpy πίνακες, επιλέξτε τους xs, ys και στη συνέχεια αποκτήστε το εννοώ:

g1_center = [np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()]
g2_center = [np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()]
g1_center, g2_center

Για να βοηθήσουμε στην επανάληψη της διαδικασίας με τα νέα κεντρικά μας σημεία, ας μετατρέψουμε τον προηγούμενο κώδικα σε συνάρτηση, ας τον εκτελέσουμε και ας δούμε αν υπήρξαν αλλαγές στον τρόπο ομαδοποίησης των σημείων:

def assigns_points_to_two_groups(g1_center, g2_center):
    points_in_g1 = []
    points_in_g2 = []
    group = []

    for p in points:
        x1, y1 = p[0], p[1]
        euclidean_distance_g1 = np.sqrt((g1_center[0] - x1)**2 + (g1_center[1] - y1)**2)
        euclidean_distance_g2 = np.sqrt((g2_center[0] - x1)**2 + (g2_center[1] - y1)**2)
        if euclidean_distance_g1 < euclidean_distance_g2:
            points_in_g1.append(p)
            group.append(1)
        else:
            points_in_g2.append(p)
            group.append(2)
    return points_in_g1, points_in_g2, group

Ας καλέσουμε τη συνάρτηση και ας αποθηκεύσουμε τα αποτελέσματά της points_in_g1, points_in_g2, να group μεταβλητές:

points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
points_in_g1, points_in_g2, group

Και επίσης σχεδιάστε το scatterplot με τα χρωματιστά σημεία για να απεικονίσετε τη διαίρεση των ομάδων:

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

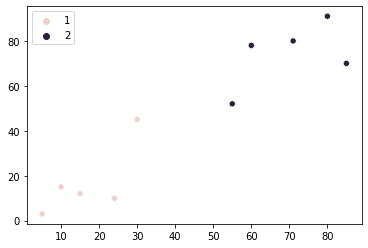
Φαίνεται ότι η ομαδοποίηση των σημείων μας είναι να πάρει καλύτερα. Ωστόσο, υπάρχουν δύο σημεία στη μέση του γραφήματος που θα μπορούσαν να αντιστοιχιστούν σε κάθε ομάδα όταν εξετάζεται η εγγύτητά τους και στις δύο ομάδες. Ο αλγόριθμος που έχουμε αναπτύξει μέχρι στιγμής εκχωρεί και τα δύο αυτά σημεία στη δεύτερη ομάδα.

Αυτό σημαίνει ότι μπορούμε πιθανώς να επαναλάβουμε τη διαδικασία για άλλη μια φορά λαμβάνοντας τα μέσα των Xs και Ys, δημιουργώντας δύο νέα κεντρικά σημεία (κεντροειδή) στις ομάδες μας και την εκ νέου ανάθεση τους με βάση την απόσταση.

Ας δημιουργήσουμε επίσης μια συνάρτηση για την ενημέρωση των κεντροειδών. Η όλη διαδικασία τώρα μπορεί να περιοριστεί σε πολλαπλές κλήσεις αυτής της συνάρτησης:

def updates_centroids(points_in_g1, points_in_g2):
    g1_center = np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()
    g2_center = np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()
    return g1_center, g2_center

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

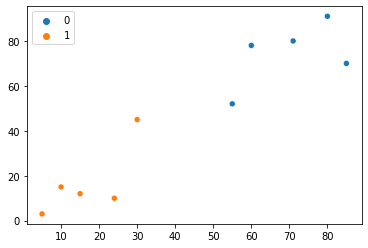
Παρατηρήστε ότι μετά από αυτήν την τρίτη επανάληψη, κάθε ένα από τα σημεία ανήκει πλέον σε διαφορετικά συμπλέγματα. Φαίνεται ότι τα αποτελέσματα βελτιώνονται – ας το κάνουμε άλλη μια φορά. Τώρα πηγαίνοντας στο τέταρτη επανάληψη της μεθόδου μας:

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

Αυτή την τέταρτη φορά πήραμε το ίδιο αποτέλεσμα όπως το προηγούμενο. Φαίνεται λοιπόν ότι οι βαθμοί μας δεν θα αλλάζουν πλέον ομάδες, το αποτέλεσμά μας έχει φτάσει σε κάποιο είδος σταθερότητας – έχει φτάσει σε αμετάβλητη κατάσταση ή συγκλίνουν. Άλλωστε έχουμε ακριβώς το ίδιο αποτέλεσμα που είχαμε οραματιστεί για τους 2 ομίλους. Μπορούμε επίσης να δούμε αν έχει νόημα αυτή η φτασμένη διαίρεση.

Ας ανακεφαλαιώσουμε γρήγορα τι έχουμε κάνει μέχρι τώρα. Χωρίσαμε τα 10 καταστήματά μας γεωγραφικά σε δύο τμήματα – ένα στις χαμηλότερες νοτιοδυτικές περιοχές και άλλα στα βορειοανατολικά. Μπορεί να είναι ενδιαφέρον να συλλέγουμε περισσότερα δεδομένα εκτός από αυτά που έχουμε ήδη – έσοδα, ημερήσιος αριθμός πελατών και πολλά άλλα. Με αυτόν τον τρόπο μπορούμε να κάνουμε μια πιο πλούσια ανάλυση και πιθανώς να δημιουργήσουμε πιο ενδιαφέροντα αποτελέσματα.

Οι μελέτες ομαδοποίησης όπως αυτή μπορούν να διεξαχθούν όταν μια ήδη καθιερωμένη επωνυμία θέλει να επιλέξει μια περιοχή για να ανοίξει ένα νέο κατάστημα. Σε αυτή την περίπτωση, υπάρχουν πολλές περισσότερες μεταβλητές που λαμβάνονται υπόψη εκτός από την τοποθεσία.

Τι σχέση έχουν όλα αυτά με τον αλγόριθμο K-Means;

Ενώ ακολουθείτε αυτά τα βήματα, ίσως έχετε αναρωτηθεί τι σχέση έχουν με τον αλγόριθμο K-Means. Η διαδικασία που έχουμε πραγματοποιήσει μέχρι τώρα είναι η Αλγόριθμος K-Means. Εν ολίγοις, προσδιορίσαμε τον αριθμό των ομάδων/συστάδων, επιλέξαμε τυχαία αρχικά σημεία και ενημερώσαμε τα κεντροειδή σε κάθε επανάληψη έως ότου τα συμπλέγματα συγκλίνουν. Βασικά έχουμε εκτελέσει ολόκληρο τον αλγόριθμο με το χέρι – διεξάγοντας προσεκτικά κάθε βήμα.

Η K σε K-Means προέρχεται από το αριθμός συστάδων που πρέπει να ρυθμιστούν πριν από την έναρξη της διαδικασίας επανάληψης. Στην περίπτωσή μας Κ = 2. Αυτό το χαρακτηριστικό μερικές φορές θεωρείται ως αρνητικός Λαμβάνοντας υπόψη ότι υπάρχουν και άλλες μέθοδοι ομαδοποίησης, όπως η Ιεραρχική Ομαδοποίηση, οι οποίες δεν χρειάζεται να έχουν προκαθορισμένο αριθμό συμπλεγμάτων.

Λόγω της χρήσης μέσων, το K-means γίνεται επίσης ευαίσθητες σε ακραίες τιμές και ακραίες τιμές – ενισχύουν τη μεταβλητότητα και δυσκολεύουν τα κεντροειδή μας να παίξουν τον ρόλο τους. Επομένως, να έχετε επίγνωση της ανάγκης να εκτελέσετε ακραίες τιμές και ανάλυση ακραίων τιμών πριν από τη διεξαγωγή μιας ομαδοποίησης χρησιμοποιώντας τον αλγόριθμο K-Means.

Επίσης, παρατηρήστε ότι τα σημεία μας ήταν τμηματικά σε ευθεία μέρη, δεν υπάρχουν καμπύλες κατά τη δημιουργία των συστάδων. Αυτό μπορεί επίσης να είναι ένα μειονέκτημα του αλγορίθμου K-Means.

Το K-Means έχει επίσης πολλά πλεονεκτήματα! Έχει καλή απόδοση μεγάλα σύνολα δεδομένων το οποίο μπορεί να γίνει δύσκολο να χειριστείτε εάν χρησιμοποιείτε ορισμένους τύπους αλγορίθμων ιεραρχικής ομαδοποίησης. Επίσης εγγυάται τη σύγκλιση, και μπορεί εύκολα γενικεύω και προσαρμόσει. Εκτός αυτού, είναι ίσως ο πιο χρησιμοποιούμενος αλγόριθμος ομαδοποίησης.

Τώρα που έχουμε διαβάσει όλα τα βήματα που εκτελούνται στον αλγόριθμο K-Means και κατανοήσαμε όλα τα πλεονεκτήματα και τα μειονεκτήματά του, μπορούμε επιτέλους να εφαρμόσουμε το K-Means χρησιμοποιώντας τη βιβλιοθήκη Scikit-Learn.

Πώς να εφαρμόσετε τον αλγόριθμο K-Means χρησιμοποιώντας Scikit-Μάθετε

Για να ελέγξουμε ξανά το αποτέλεσμά μας, ας κάνουμε αυτή τη διαδικασία ξανά, αλλά τώρα χρησιμοποιώντας 3 γραμμές κώδικα με sklearn:

from sklearn.cluster import KMeans


kmeans = KMeans(n_clusters=2, random_state=42) 
kmeans.fit(points)
kmeans.labels_

Εδώ, οι ετικέτες είναι ίδιες με τις προηγούμενες ομάδες μας. Ας σχεδιάσουμε γρήγορα το αποτέλεσμα:

sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Το οικόπεδο που προκύπτει είναι το ίδιο με αυτό της προηγούμενης ενότητας.

Με το Scikit-Learn, μπορείτε επίσης να αρχικοποιήσετε το K-Means για ταχύτερη σύγκλιση ρυθμίζοντας το init='k-means++' διαφωνία. Με ευρύτερους όρους, K-Means++ ακόμα επιλέγει το k αρχικό κέντρο συστάδων τυχαία ακολουθώντας ομοιόμορφη κατανομή. Στη συνέχεια, κάθε επόμενο κέντρο συμπλέγματος επιλέγεται από τα υπόλοιπα σημεία δεδομένων όχι με τον υπολογισμό μόνο ενός μέτρου απόστασης – αλλά με τη χρήση πιθανότητας. Η χρήση της πιθανότητας επιταχύνει τον αλγόριθμο και είναι χρήσιμη όταν αντιμετωπίζετε πολύ μεγάλα σύνολα δεδομένων.

The Elbow Method – Επιλέγοντας τον καλύτερο αριθμό ομάδων

Μέχρι εδώ καλά! Συγκεντρώσαμε 10 καταστήματα με βάση την Ευκλείδεια απόσταση μεταξύ σημείων και κεντροειδών. Τι γίνεται όμως με αυτά τα δύο σημεία στη μέση του γραφήματος που είναι λίγο πιο δύσκολο να συγκεντρωθούν; Δεν θα μπορούσαν να κάνουν και ξεχωριστή ομάδα; Μήπως τελικά κάναμε λάθος επιλέγοντας; K = 2 ομάδες; Ίσως όντως είχαμε K = 3 ομάδες; Θα μπορούσαμε να έχουμε περισσότερες από τρεις ομάδες και να μην το γνωρίζουμε.

Το ερώτημα που τίθεται εδώ είναι πώς να προσδιορίσετε τον αριθμό των ομάδων (K) στο K-Means. Για να απαντήσουμε σε αυτήν την ερώτηση, πρέπει να καταλάβουμε εάν θα υπήρχε ένα «καλύτερο» σύμπλεγμα για μια διαφορετική τιμή του K.

Ο αφελής τρόπος για να το ανακαλύψετε είναι η ομαδοποίηση σημείων με διαφορετικές τιμές του K, Έτσι, για K=2, K=3, K=4, και ούτω καθεξής:

for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 

Αλλά, ομαδοποίηση σημείων για διαφορετικά Ks alone δεν θα είναι αρκετό για να καταλάβουμε αν επιλέξαμε την ιδανική τιμή για K. Χρειαζόμαστε έναν τρόπο αξιολόγησης της ποιότητας ομαδοποίησης για καθένα K διαλέξαμε.

Χειροκίνητος Υπολογισμός του Μέσα σε άθροισμα τετραγώνων (WCSS)

Εδώ είναι το ιδανικό μέρος για να εισαγάγετε ένα μέτρο του πόσο κοντά είναι τα συγκεντρωμένα σημεία μας. Ουσιαστικά περιγράφει πόσο διακύμανση έχουμε μέσα σε ένα ενιαίο σύμπλεγμα. Το μέτρο αυτό ονομάζεται Μέσα σε άθροισμα τετραγώνων, ή WCSS εν συντομία. Όσο μικρότερο είναι το WCSS, τόσο πιο κοντά είναι τα σημεία μας, επομένως έχουμε ένα πιο καλοσχηματισμένο σύμπλεγμα. Ο τύπος WCSS μπορεί να χρησιμοποιηθεί για οποιοδήποτε αριθμό συμπλεγμάτων:

$$
WCSS = άθροισμα (Pi_1 – Centroid_1)^2 + cdots + sum(Pi_n – Centroid_n)^2
$$

Τώρα μπορούμε να υποθέσουμε ότι επιλέξαμε να έχουμε δύο συμπλέγματα και προσπαθήσαμε να εφαρμόσουμε το WCSS για να κατανοήσουμε καλύτερα τι είναι το WCSS και πώς να το χρησιμοποιήσουμε. Όπως δηλώνει ο τύπος, πρέπει να αθροίσουμε τις τετραγωνικές διαφορές μεταξύ όλων των σημείων του συμπλέγματος και των κεντροειδών. Έτσι, αν ο πρώτος μας βαθμός από την πρώτη ομάδα είναι (5, 3) και το τελευταίο μας κέντρο (μετά τη σύγκλιση) της πρώτης ομάδας είναι (16.8, 17.0), το WCSS θα είναι:

$$
WCSS = άθροισμα((5,3) – (16.8, 17.0))^2
$$

$$
WCSS = άθροισμα ((5-16.8) + (3-17.0))^2
$$

$$
WCSS = άθροισμα ((-11.8) + (-14.0))^2
$$

$$
WCSS = άθροισμα ((-25.8))^2
$$

$$
WCSS = 335.24
$$

Αυτό το παράδειγμα δείχνει πώς υπολογίζουμε το WCSS για ένα σημείο από το σύμπλεγμα. Αλλά το σύμπλεγμα συνήθως περιέχει περισσότερα από ένα σημεία και πρέπει να τα λάβουμε όλα υπόψη κατά τον υπολογισμό του WCSS. Θα το κάνουμε αυτό ορίζοντας μια συνάρτηση που λαμβάνει ένα σύμπλεγμα σημείων και κεντροειδών και επιστρέφει το άθροισμα των τετραγώνων:

def sum_of_squares(cluster, centroid):
    squares = []
    for p in cluster:
        squares.append((p - centroid)**2)
        ss = np.array(squares).sum()
    return ss

Τώρα μπορούμε να πάρουμε το άθροισμα των τετραγώνων για κάθε σύμπλεγμα:

g1 = sum_of_squares(points_in_g1, g1_center)
g2 = sum_of_squares(points_in_g2, g2_center)

Και συνοψίστε τα αποτελέσματα για να λάβετε το σύνολο WCSS:

g1 + g2

Αυτο εχει ως αποτελεσμα:

2964.3999999999996

Έτσι, στην περίπτωσή μας, όταν K ισούται με 2, το συνολικό WCSS είναι 2964.39. Τώρα, μπορούμε να αλλάξουμε Ks και να υπολογίσουμε το WCSS για όλα αυτά. Με αυτόν τον τρόπο, μπορούμε να πάρουμε μια εικόνα για το τι K θα πρέπει να επιλέξουμε να κάνουμε την ομαδοποίηση μας να αποδώσει καλύτερα.

Υπολογισμός WCSS Χρησιμοποιώντας Scikit-Μάθετε

Ευτυχώς, δεν χρειάζεται να υπολογίσουμε με μη αυτόματο τρόπο το WCSS για το καθένα K. Αφού εκτελέσουμε την ομαδοποίηση K-Means για τον δεδομένο αριθμό συστάδων, μπορούμε να λάβουμε το WCSS του χρησιμοποιώντας το inertia_ Χαρακτηριστικό. Τώρα, μπορούμε να επιστρέψουμε στα K-Means μας for βρόχο, χρησιμοποιήστε το για να εναλλάξετε τον αριθμό των συμπλεγμάτων και απαριθμήστε τις αντίστοιχες τιμές WCSS:

wcss = [] 
for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 
    wcss.append(kmeans.inertia_)
wcss

Παρατηρήστε ότι η δεύτερη τιμή στη λίστα είναι ακριβώς η ίδια που έχουμε υπολογίσει πριν K = 2:

[18272.9, # For k=1 
 2964.3999999999996, # For k=2
 1198.75, # For k=3
 861.75,
 570.5,
 337.5,
 175.83333333333334,
 79.5,
 17.0,
 0.0]

Για να οπτικοποιήσουμε αυτά τα αποτελέσματα, ας σχεδιάσουμε το δικό μας Ks μαζί με τις τιμές WCSS:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
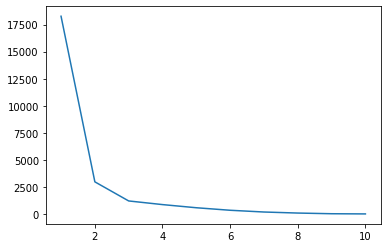
plt.plot(ks, wcss)

Υπάρχει διακοπή σε οικόπεδο όταν x = 2, ένα χαμηλό σημείο στη γραμμή, και ένα ακόμη χαμηλότερο όταν x = 3. Προσέξτε ότι μας θυμίζει το σχήμα αγκώνα. Σχεδιάζοντας τα Ks μαζί με το WCSS, χρησιμοποιούμε το Μέθοδος αγκώνα για να επιλέξετε τον αριθμό των Κ. Και το Το επιλεγμένο Κ είναι ακριβώς το χαμηλότερο σημείο του αγκώνα, έτσι, θα ήταν 3 αντί του 2, στην περίπτωσή μας:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
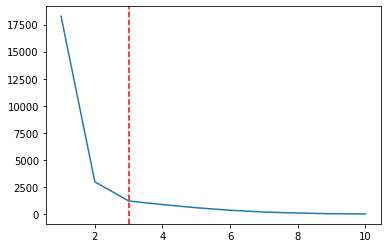
plt.plot(ks, wcss);
plt.axvline(3, linestyle='--', color='r')

Μπορούμε να εκτελέσουμε ξανά τον αλγόριθμο συμπλέγματος K-Means, για να δούμε πώς θα φαίνονται τα δεδομένα μας τρεις συστάδες:

kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(points)
sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Ήμασταν ήδη ευχαριστημένοι με δύο συστάδες, αλλά σύμφωνα με τη μέθοδο του αγκώνα, τρία συμπλέγματα θα ταίριαζαν καλύτερα στα δεδομένα μας. Σε αυτήν την περίπτωση, θα είχαμε τρία είδη καταστημάτων αντί για δύο. Πριν χρησιμοποιήσουμε τη μέθοδο του αγκώνα, σκεφτήκαμε νοτιοδυτικά και βορειοανατολικά συμπλέγματα καταστημάτων, τώρα έχουμε και καταστήματα στο κέντρο. Ίσως αυτό θα μπορούσε να είναι μια καλή τοποθεσία για να ανοίξετε ένα άλλο κατάστημα, καθώς θα είχε λιγότερο ανταγωνισμό κοντά.

Εναλλακτικά Μέτρα Ποιότητας Cluster

Υπάρχουν επίσης άλλα μέτρα που μπορούν να χρησιμοποιηθούν κατά την αξιολόγηση της ποιότητας των συστάδων:

• Σκιαγραφία Σιλουέτα – αναλύει όχι μόνο την απόσταση μεταξύ σημείων εντός του συμπλέγματος αλλά και μεταξύ των ίδιων των συστάδων
• Μεταξύ συστάδων Άθροισμα τετραγώνων (BCSS) – μετρική συμπληρωματική του WCSS
• Σφάλμα αθροίσματος τετραγώνων (SSE)
• Μέγιστη ακτίνα – μετρά τη μεγαλύτερη απόσταση από ένα σημείο στο κέντρο του
• Μέση ακτίνα – το άθροισμα της μεγαλύτερης απόστασης από ένα σημείο στο κέντρο του διαιρεμένο με τον αριθμό των συστάδων.

Συνιστάται να πειραματιστείτε και να γνωρίσετε καθένα από αυτά, καθώς ανάλογα με το πρόβλημα, ορισμένες από τις εναλλακτικές λύσεις μπορεί να είναι πιο εφαρμόσιμες από τις πιο ευρέως χρησιμοποιούμενες μετρήσεις (WCSS και Silhouette Score).

Στο τέλος, όπως συμβαίνει με πολλούς αλγόριθμους επιστήμης δεδομένων, θέλουμε να μειώσουμε τη διακύμανση μέσα σε κάθε σύμπλεγμα και να μεγιστοποιήσουμε τη διακύμανση μεταξύ διαφορετικών συστάδων. Έτσι έχουμε πιο καθορισμένα και χωριστά συμπλέγματα.

Εφαρμογή K-Means σε άλλο σύνολο δεδομένων

Ας χρησιμοποιήσουμε όσα μάθαμε σε ένα άλλο σύνολο δεδομένων. Αυτή τη φορά, θα προσπαθήσουμε να βρούμε ομάδες παρόμοιων κρασιών.

Ξεκινάμε με την εισαγωγή pandas για να διαβάσετε το wine-clustering CSV (Τιμές διαχωρισμένες με κόμμα) αρχείο σε α Dataframe δομή:

import pandas as pd

df = pd.read_csv('wine-clustering.csv')

Αφού το φορτώσουμε, ας ρίξουμε μια ματιά στις πέντε πρώτες εγγραφές δεδομένων με το head() μέθοδος:

df.head()

Αυτο εχει ως αποτελεσμα:

	Alcohol 	Malic_Acid 	Ash 	Ash_Alcanity 	Magnesium 	Total_Phenols 	Flavanoids 	Nonflavanoid_Phenols 	Proanthocyanins 	Color_Intensity 	Hue 	OD280 	Proline
0 	14.23 		1.71 		2.43 	15.6 			127 		2.80 			3.06 		0.28 					2.29 				5.64 				1.04 	3.92 	1065
1 	13.20 		1.78 		2.14 	11.2 			100 		2.65 			2.76 		0.26 					1.28 				4.38 				1.05 	3.40 	1050
2 	13.16 		2.36 		2.67 	18.6 			101 		2.80 			3.24 		0.30 					2.81 				5.68 				1.03 	3.17 	1185
3 	14.37 		1.95 		2.50 	16.8 			113 		3.85 			3.49 		0.24 					2.18 				7.80 				0.86 	3.45 	1480
4 	13.24 		2.59 		2.87 	21.0 			118 		2.80 			2.69 		0.39 					1.82 				4.32 				1.04 	2.93 	735

Έχουμε πολλές μετρήσεις ουσιών που υπάρχουν στα κρασιά. Εδώ, επίσης, δεν θα χρειαστεί να μετασχηματίσουμε κατηγορικές στήλες επειδή όλες είναι αριθμητικές. Τώρα, ας ρίξουμε μια ματιά στα περιγραφικά στατιστικά στοιχεία με το describe() μέθοδος:

df.describe().T 

Ο πίνακας περιγραφής:

 						count 	mean 		std 		min 	25% 	50% 	75% 		max
Alcohol 				178.0 	13.000618 	0.811827 	11.03 	12.3625 13.050 	13.6775 	14.83
Malic_Acid 				178.0 	2.336348 	1.117146 	0.74 	1.6025 	1.865 	3.0825 		5.80
Ash 					178.0 	2.366517 	0.274344 	1.36 	2.2100 	2.360 	2.5575 		3.23
Ash_Alcanity 			178.0 	19.494944 	3.339564 	10.60 	17.2000 19.500 	21.5000 	30.00
Magnesium 				178.0 	99.741573 	14.282484 	70.00 	88.0000 98.000 	107.0000 	162.00
Total_Phenols 			178.0 	2.295112 	0.625851 	0.98 	1.7425 	2.355 	2.8000 		3.88
Flavanoids 				178.0 	2.029270 	0.998859 	0.34 	1.2050 	2.135 	2.8750 		5.08
Nonflavanoid_Phenols 	178.0 	0.361854 	0.124453 	0.13 	0.2700 	0.340 	0.4375 		0.66
Proanthocyanins 		178.0 	1.590899 	0.572359 	0.41 	1.2500 	1.555 	1.9500 		3.58
Color_Intensity 		178.0 	5.058090 	2.318286 	1.28 	3.2200 	4.690 	6.2000 		13.00
Hue 					178.0 	0.957449 	0.228572 	0.48 	0.7825 	0.965 	1.1200 		1.71
OD280 					178.0 	2.611685 	0.709990 	1.27 	1.9375 	2.780 	3.1700 		4.00
Proline 				178.0 	746.893258 	314.907474 	278.00 	500.500 673.500 985.0000 	1680.00

Βλέποντας τον πίνακα είναι ξεκάθαρο ότι υπάρχουν κάποια μεταβλητότητα στα δεδομένα – για ορισμένες στήλες όπως π.χ Alchool υπάρχουν περισσότερα, και για άλλα, όπως π.χ Malic_Acid, πιο λιγο. Τώρα μπορούμε να ελέγξουμε αν υπάρχουν null, ή NaN τιμές στο σύνολο δεδομένων μας:

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 13 columns):
 #   Column                Non-Null Count  Dtype  
---  ------                --------------  -----  
 0   Alcohol               178 non-null    float64
 1   Malic_Acid            178 non-null    float64
 2   Ash                   178 non-null    float64
 3   Ash_Alcanity          178 non-null    float64
 4   Magnesium             178 non-null    int64  
 5   Total_Phenols         178 non-null    float64
 6   Flavanoids            178 non-null    float64
 7   Nonflavanoid_Phenols  178 non-null    float64
 8   Proanthocyanins       178 non-null    float64
 9   Color_Intensity       178 non-null    float64
 10  Hue                   178 non-null    float64
 11  OD280                 178 non-null    float64
 12  Proline               178 non-null    int64  
dtypes: float64(11), int64(2)
memory usage: 18.2 KB

Δεν υπάρχει ανάγκη απόθεσης ή εισαγωγής δεδομένων, δεδομένου ότι δεν υπάρχουν κενές τιμές στο σύνολο δεδομένων. Μπορούμε να χρησιμοποιήσουμε ένα Seaborn pairplot() για να δείτε τη διανομή δεδομένων και να ελέγξετε εάν το σύνολο δεδομένων σχηματίζει ζεύγη στηλών που μπορεί να είναι ενδιαφέροντα για ομαδοποίηση:

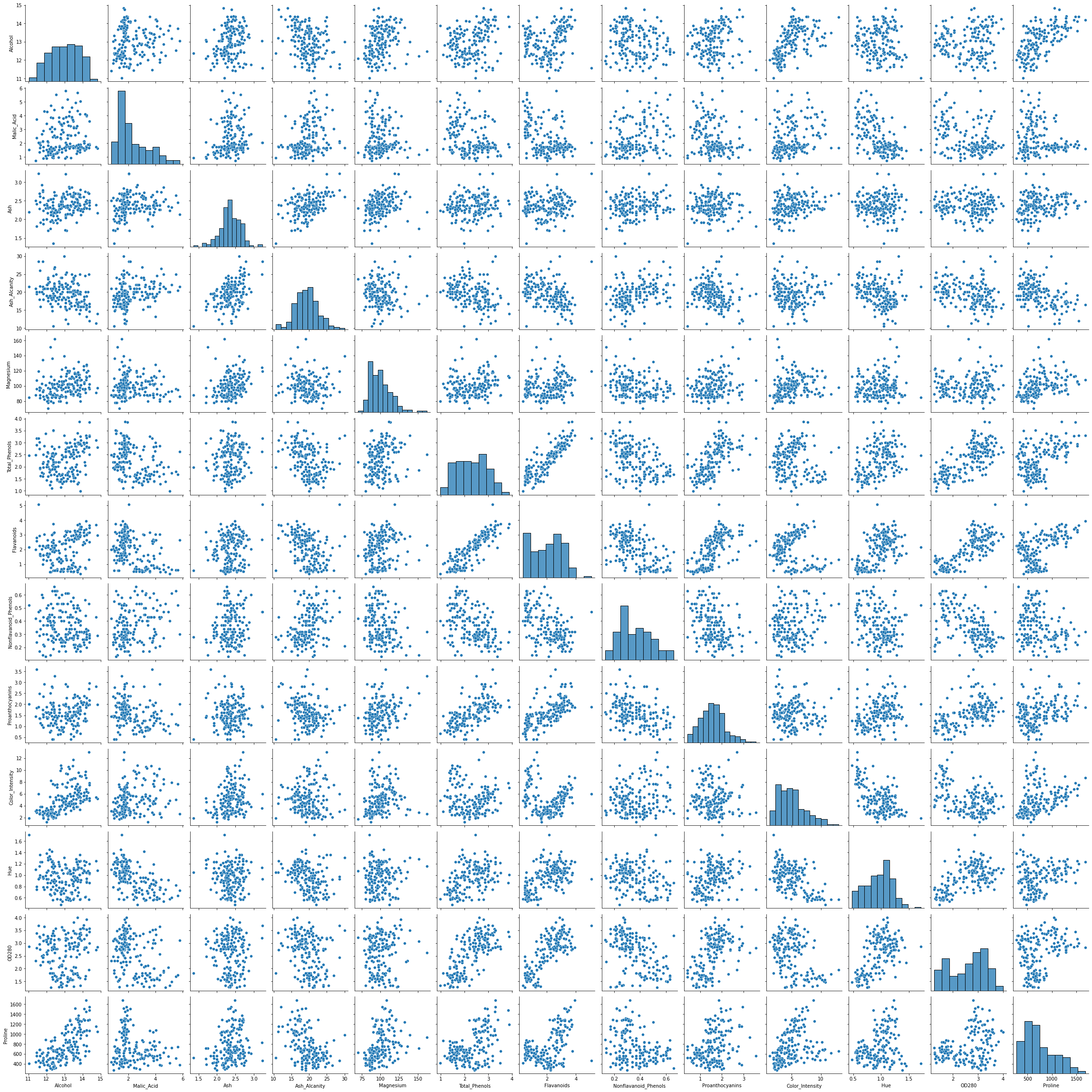
sns.pairplot(df)

Εξετάζοντας το ζεύγος, δύο στήλες φαίνονται πολλά υποσχόμενες για σκοπούς ομαδοποίησης – Alcohol και OD280 (που είναι μια μέθοδος για τον προσδιορισμό της συγκέντρωσης πρωτεΐνης στα κρασιά). Φαίνεται ότι υπάρχουν 3 διακριτές συστάδες σε οικόπεδα που συνδυάζουν δύο από αυτές.

Υπάρχουν και άλλες στήλες που φαίνεται να συσχετίζονται επίσης. Κυρίως Alcohol και Total_Phenols, να Alcohol και Flavanoids. Έχουν μεγάλες γραμμικές σχέσεις που μπορούν να παρατηρηθούν στο pairplot.

Επειδή η εστίασή μας είναι η ομαδοποίηση με K-Means, ας επιλέξουμε ένα ζευγάρι στηλών, ας πούμε Alcohol και OD280και δοκιμάστε τη μέθοδο elbow για αυτό το σύνολο δεδομένων.

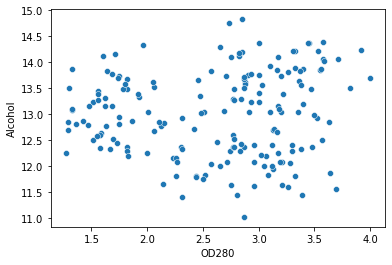
Ας σχεδιάσουμε το διάγραμμα διασποράς με αυτές τις δύο στήλες να είναι ο άξονάς του για να ρίξουμε μια πιο προσεκτική ματιά στα σημεία που θέλουμε να χωρίσουμε σε ομάδες:

sns.scatterplot(data=df, x='OD280', y='Alcohol')

Τώρα μπορούμε να ορίσουμε τις στήλες μας και να χρησιμοποιήσουμε τη μέθοδο elbow για να προσδιορίσουμε τον αριθμό των συστάδων. Θα ξεκινήσουμε επίσης τον αλγόριθμο με kmeans++ απλά για να βεβαιωθείτε ότι συγκλίνει πιο γρήγορα:

values = df[['OD280', 'Alcohol']]

wcss_wine = [] 
for i in range(1, 11): 
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(values) 
    wcss_wine.append(kmeans.inertia_)

Έχουμε υπολογίσει το WCSS, ώστε να μπορούμε να σχεδιάσουμε τα αποτελέσματα:

clusters_wine = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
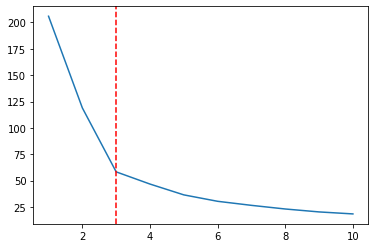
plt.plot(clusters_wine, wcss_wine)
plt.axvline(3, linestyle='--', color='r')

Σύμφωνα με τη μέθοδο του αγκώνα θα πρέπει να έχουμε 3 συστάδες εδώ. Για το τελευταίο βήμα, ας ομαδοποιήσουμε τα σημεία μας σε 3 ομάδες και ας σχεδιάσουμε τα συμπλέγματα που προσδιορίζονται με χρώματα:

kmeans_wine = KMeans(n_clusters=3, random_state=42)
kmeans_wine.fit(values)
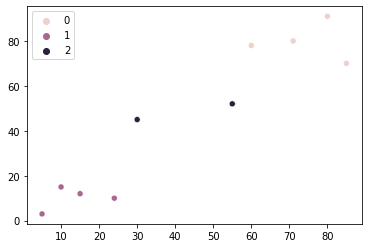
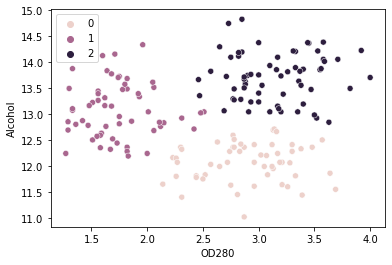
sns.scatterplot(x = values['OD280'], y = values['Alcohol'], hue=kmeans_wine.labels_)

Μπορούμε να δούμε συστάδες 0, 1, να 2 στο γράφημα. Με βάση την ανάλυσή μας, ομάδα 0 έχει κρασιά με υψηλότερη περιεκτικότητα σε πρωτεΐνη και χαμηλότερο αλκοόλ, ομάδα 1 έχει κρασιά με υψηλότερη περιεκτικότητα σε αλκοόλ και χαμηλή πρωτεΐνη, και ομάδα 2 έχει τόσο υψηλή περιεκτικότητα σε πρωτεΐνη όσο και υψηλό αλκοόλ στα κρασιά του.

Αυτό είναι ένα πολύ ενδιαφέρον σύνολο δεδομένων και σας ενθαρρύνω να προχωρήσετε περαιτέρω στην ανάλυση ομαδοποιώντας τα δεδομένα μετά την κανονικοποίηση και PCA – επίσης ερμηνεύοντας τα αποτελέσματα και βρίσκοντας νέες συνδέσεις.

Συμπέρασμα

Κ-Μέσα Η ομαδοποίηση είναι ένας απλός αλλά πολύ αποτελεσματικός αλγόριθμος μηχανικής μάθησης χωρίς επίβλεψη για ομαδοποίηση δεδομένων. Συγκεντρώνει δεδομένα με βάση την Ευκλείδεια απόσταση μεταξύ των σημείων δεδομένων. Ο αλγόριθμος ομαδοποίησης K-Means έχει πολλές χρήσεις για την ομαδοποίηση εγγράφων κειμένου, εικόνων, βίντεο και πολλά άλλα.