1ICFO-Institut de Ciencies Fotoniques, Ινστιτούτο Επιστήμης και Τεχνολογίας της Βαρκελώνης, 08860 Castelldefels, Ισπανία
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Βαρκελώνη, Ισπανία
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, France
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Βαρκελώνη, Ισπανία
Βρείτε αυτό το άρθρο ενδιαφέρουσα ή θέλετε να συζητήσετε; Scite ή αφήστε ένα σχόλιο για το SciRate.
Περίληψη
Οι αμοιβαία αμερόληπτες βάσεις αντιστοιχούν σε εξαιρετικά χρήσιμα ζεύγη μετρήσεων στην κβαντική θεωρία πληροφοριών. Στη μικρότερη σύνθετη διάσταση, έξι, είναι γνωστό ότι υπάρχουν μεταξύ τριών και επτά αμοιβαία αμερόληπτων βάσεων, με μια εικασία δεκαετιών, γνωστή ως εικασία του Zauner, που δηλώνει ότι υπάρχουν το πολύ τρεις. Εδώ αντιμετωπίζουμε την εικασία του Zauner αριθμητικά μέσω της κατασκευής ανισοτήτων Bell για κάθε ζεύγος ακεραίων $n,d ge 2$ που μπορούν να παραβιαστούν στο μέγιστο στην διάσταση $d$ εάν και μόνο εάν υπάρχουν $n$ MUB σε αυτή τη διάσταση. Ως εκ τούτου, μετατρέπουμε την εικασία του Zauner σε ένα πρόβλημα βελτιστοποίησης, το οποίο αντιμετωπίζουμε με τρεις αριθμητικές μεθόδους: βελτιστοποίηση see-saw, μη γραμμικό ημικαθορισμένο προγραμματισμό και τεχνικές Monte Carlo. Και οι τρεις μέθοδοι προσδιορίζουν σωστά τις γνωστές περιπτώσεις σε χαμηλές διαστάσεις και όλες υποδηλώνουν ότι δεν υπάρχουν τέσσερις αμοιβαία αμερόληπτες βάσεις στη διάσταση έξι, με όλες να βρίσκουν τις ίδιες βάσεις που βελτιστοποιούν αριθμητικά την αντίστοιχη ανισότητα Bell. Επιπλέον, αυτοί οι αριθμητικοί βελτιστοποιητές φαίνεται να συμπίπτουν με τις «τέσσερις πιο απομακρυσμένες βάσεις» στη διάσταση έξι, που βρέθηκαν μέσω της αριθμητικής βελτιστοποίησης ενός μέτρου απόστασης στο [Σ. Raynal, X. Lü, B.-G. Englert, {Phys. Αναθ. Α}, {83} 062303 (2011)]. Τέλος, τα αποτελέσματα του Μόντε Κάρλο υποδηλώνουν ότι υπάρχουν το πολύ τρία MUB στη διάσταση δέκα.
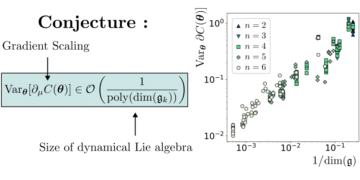
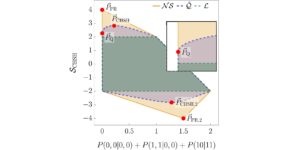
Προτεινόμενη εικόνα: Η σχετική διαφορά μεταξύ της τιμής των ανισοτήτων Bell με την υπόθεση ότι υπάρχουν n MUB στη διάσταση d και της τιμής που βρέθηκε με τις αριθμητικές μας μεθόδους. Οι μηδενικές τιμές σημαίνουν ότι οι μέθοδοι βρήκαν n MUB στην διάσταση d, ενώ οι μη μηδενικές τιμές σημαίνουν ότι οι μέθοδοι δεν βρήκαν n MUB στην διάσταση d. Όλες οι γνωστές περιπτώσεις (διαστάσεις δύο έως πέντε και διάσταση έξι με δύο και τρία MUB) προσδιορίζονται σωστά από τους αριθμούς. Στη διάσταση έξι, καμία από τις μεθόδους δεν βρίσκει τέσσερα MUB και όλες οι μέθοδοι συγκλίνουν στο ίδιο σύνολο τεσσάρων βάσεων.
Δημοφιλή περίληψη
Παρά την ευρεία χρήση τους, παραμένουν ανοιχτά ερωτήματα σχετικά με τη δομή των MUB. Κυρίως, ο μέγιστος αριθμός μετρήσεων που είναι αμερόληπτες κατά ζεύγη ("ο αριθμός των MUB") είναι άγνωστος εάν η διάσταση του κβαντικού συστήματος είναι ένας σύνθετος αριθμός. Συγκεκριμένα, στη διάσταση έξι γνωρίζουμε μόνο ότι ο αριθμός των MUB είναι μεταξύ τριών και επτά. Μια μακροχρόνια ανοιχτή εικασία είναι αυτή του Zauner, που δηλώνει ότι δεν υπάρχουν περισσότερα από τρία MUB στη διάσταση έξι. Αυτή η εικασία δεκαετιών υποστηρίζεται από ορισμένα αριθμητικά στοιχεία, αλλά δεν υπάρχει καμία απόδειξη μέχρι σήμερα.
Σε αυτό το έργο αντιμετωπίζουμε την εικασία του Zauner μέσω της μη-τοπικότητας του Bell. Η μη τοπικότητα του κουδουνιού αφορά δύο πειραματιστές που δεν επιτρέπεται να επικοινωνούν, αλλά μπορούν να μοιραστούν κάποιες συσχετίσεις με τη μορφή κλασικής τυχαιότητας ή κοινής κβαντικής κατάστασης. Έχει αποδειχθεί ότι η κοινή χρήση κβαντικών πόρων μπορεί να οδηγήσει σε πειραματικά δεδομένα που δεν μπορούν να εξηγηθούν από την κλασική φυσική (ακριβέστερα, από τα λεγόμενα τοπικά κρυφά μοντέλα μεταβλητών). Αυτό είναι γνωστό ως θεώρημα του Bell, και έχει επαληθευτεί πειραματικά την τελευταία δεκαετία. Η μαρτυρία της μη κλασικότητας των πειραματικών δεδομένων γίνεται συνήθως μέσω των αποκαλούμενων ανισοτήτων Bell, οι οποίες είναι συναρτήσεις των πιθανοτήτων του αποτελέσματος της μέτρησης που εμφανίζονται στο πείραμα. Τα κλασικά δεδομένα πρέπει να ικανοποιούν τις ανισότητες Bell, ενώ τα κβαντικά δεδομένα μπορεί να τις παραβιάζουν.
Πρόσφατα, βρέθηκαν ανισότητες Bell που παραβιάζονται στο μέγιστο εάν ένα από τα μέρη χρησιμοποιεί ένα ζεύγος μετρήσεων MUB μιας δεδομένης διάστασης. Σε αυτήν την εργασία, επεκτείνουμε αυτές τις ανισότητες σε νέες, οι οποίες παραβιάζονται στο μέγιστο από έναν επιλεγμένο αριθμό μετρήσεων MUB σε μια δεδομένη διάσταση. Επιπλέον, εάν η διάσταση στο πείραμα είναι σταθερή, η μέγιστη παραβίαση λαμβάνεται εάν και μόνο εάν οι χρησιμοποιούμενες μετρήσεις αντιστοιχούν στον επιλεγμένο αριθμό MUB στη δεδομένη διάσταση. Επομένως, το να αποφασίσετε εάν ένας επιλεγμένος αριθμός MUB υπάρχει σε μια δεδομένη διάσταση ισοδυναμεί με την εύρεση της μέγιστης παραβίασης της αντίστοιχης ανισότητας Bell σε αυτή τη σταθερή διάσταση.
Ενώ η εύρεση αυτής της μέγιστης παραβίασης είναι γενικά ένα δύσκολο πρόβλημα, χρησιμοποιούμε τρεις διαφορετικές αριθμητικές μεθόδους ως μια προσπάθεια να βρούμε τη μέγιστη παραβίαση των ανισοτήτων μας Bell σε μια σταθερή διάσταση. Δύο από αυτές τις μεθόδους είναι παραλλαγές τεχνικών ημικαθοριστικού προγραμματισμού, ενώ η τρίτη είναι εμπνευσμένη από τη στατιστική φυσική και ονομάζεται προσομοίωση ανόπτησης. Ενώ όλες αυτές οι μέθοδοι είναι ευρετικές -δηλαδή, δεν υπάρχει εγγύηση ότι θα βρουν το πραγματικό βέλτιστο του προβλήματος- μπορεί κανείς να μετρήσει την απόδοσή τους εφαρμόζοντάς τες σε προβλήματα βελτιστοποίησης των οποίων το βέλτιστο είναι γνωστό. Συγκεκριμένα, διαπιστώνουμε ότι και οι τρεις μέθοδοι είναι σωστά σε θέση να αναγνωρίσουν μετρήσεις MUB στις περιπτώσεις που είναι γνωστό ότι υπάρχουν. Επιπλέον, στις περιπτώσεις που είναι γνωστό ότι δεν υπάρχουν, και οι τρεις μέθοδοι συγκλίνουν στο ίδιο σύνολο μετρήσεων μέχρι αριθμητικής ακρίβειας. Στη συνέχεια εφαρμόζουμε τις μεθόδους μας στην πρώτη άγνωστη περίπτωση, δηλαδή τέσσερα MUB στη διάσταση έξι. Καμία από τις μεθόδους δεν είναι σε θέση να αναγνωρίσει τέσσερα MUB στη διάσταση έξι, αλλά και πάλι όλες συγκλίνουν στο ίδιο σύνολο τεσσάρων μετρήσεων μέχρι αριθμητικής ακρίβειας. Επιπλέον, η τεχνική προσομοίωσης ανόπτησης δεν βρίσκει τέσσερα MUB στην επόμενη σύνθετη διάσταση, διάσταση δέκα. Επομένως, ενώ δεν μπορούν να γίνουν αυστηροί ισχυρισμοί λόγω της ευρετικής φύσης των τεχνικών μας, τα αποτελέσματά μας υποστηρίζουν την εικασία του Zauner από τη νέα προοπτική της μη τοπικότητας Bell.
► Δεδομένα BibTeX
► Αναφορές
[1] ID Ιβάνοβιτς. Γεωμετρική περιγραφή προσδιορισμού ποσοτικής κατάστασης. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Κβαντική κρυπτογραφία: Διανομή δημόσιου κλειδιού και ρίψη νομισμάτων. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] Artur K. Ekert. Κβαντική κρυπτογραφία βασισμένη στο θεώρημα του Bell. Phys. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] Dagmar Bruß. Βέλτιστη υποκλοπή στην κβαντική κρυπτογραφία με έξι καταστάσεις. Phys. Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques και Mohamed Bourennane. Κβαντικοί κώδικες τυχαίας πρόσβασης χρησιμοποιώντας μεμονωμένα συστήματα επιπέδου $d$. Phys. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas και Jędrzej Kaniewski. Αυτοέλεγχος αμοιβαία αμερόληπτων βάσεων στο σενάριο προετοιμασίας και μέτρησης. Phys. Αναθ. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci και N. Gisin. Ανισότητα κουδουνιού για qunits με δυαδικές μετρήσεις. Quantum Info. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos και Remigiusz Augusiak. Μέγιστη μη τοπικότητα από τη μέγιστη εμπλοκή και αμοιβαία αμερόληπτες βάσεις και αυτοέλεγχος κβαντικών συστημάτων δύο qutrit. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal και Jędrzej Kaniewski. Αμοιβαία αμερόληπτες βάσεις και συμμετρικές πληροφοριακά ολοκληρωμένες μετρήσεις στα πειράματα Bell. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https://doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson και Karol Życzkowski. Σε αμοιβαία αμερόληπτες βάσεις. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] William K Wootters και Brian D Fields. Βέλτιστος προσδιορισμός κατάστασης με αμοιβαία αμερόληπτες μετρήσεις. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan και Thomas Beth. Νέα κατασκευή αμοιβαία αμερόληπτων βάσεων σε τετράγωνες διαστάσεις. Quantum Info. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[13] Μιχάλι Βάινερ. Ένα κενό για τον μέγιστο αριθμό αμοιβαία αμερόληπτων βάσεων. Proc. Amer. Μαθηματικά. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Γκέρχαρντ Ζάουνερ. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Διδακτορική διατριβή, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep και Pawel Wocjan. Αμοιβαία αμερόληπτες βάσεις και ορθογώνιες αποσυνθέσεις αλγεβρών Lie. Quantum Info. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[16] Stephen Brierley και Stefan Weigert. Κατασκευάζοντας αμοιβαία αμερόληπτες βάσεις στη διάσταση έξι. Phys. Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi και Mihály Weiner. Ένα γενικευμένο πρόβλημα Pauli και μια άπειρη οικογένεια MUB-τριδύμων στη διάσταση 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, Μάιος 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer και Afaq Tahir. Στοιχεία υπέρ και κατά της εικασίας MUB του Zauner στο $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https://doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling και Sven Polak. Αμοιβαία αμερόληπτες βάσεις: πολυωνυμική βελτιστοποίηση και συμμετρία. 2021. doi:10.48550/arXiv.2111.05698.
https://doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej και Karol Życzkowski. Αμοιβαία αμερόληπτες βάσεις και πίνακες Hadamard τάξης έξι. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] Philippe Raynal, Xin Lü και Berthold-Georg Englert. Αμοιβαία αμερόληπτες βάσεις σε έξι διαστάσεις: Οι τέσσερις πιο απομακρυσμένες βάσεις. Phys. Αναθ. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz και Marcin Pawłowski. Συνδέσεις μεταξύ αμοιβαία αμερόληπτων βάσεων και κβαντικών κωδίκων τυχαίας πρόσβασης. Phys. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani και Stephanie Wehner. Μη τοπική καμπάνα. Αναθ. Mod Phys., 86: 419–478, 2014. doi: 10.1103 / RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOSEK ApS. MOSEK Fusion API για C++ 9.2.49, 2021. URL: https://docs.mosek.com/9.2/cxxfusion/index.html.
https://docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe και Kouhei Harada. Μια μέθοδος αρχέγονου-διπλού εσωτερικού σημείου για μη γραμμικό ημικαθορισμένο προγραμματισμό. Mathematical programming, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] Ο Stephen Boyd και ο Lieven Vandenberghe. Κυρτή Βελτιστοποίηση. Cambridge University Press, 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt και MP Vecchi. Βελτιστοποίηση με προσομοίωση ανόπτησης. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller και Edward Teller. Εξίσωση υπολογισμών καταστάσεων από γρήγορες υπολογιστικές μηχανές. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] Miguel Navascués, Stefano Pironio και Antonio Acín. Οριοθετώντας το σύνολο των κβαντικών συσχετισμών. Phys. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Αναφέρεται από
Αυτό το Βιβλίο δημοσιεύεται στο Quantum στο πλαίσιο του Creative Commons Attribution 4.0 Διεθνής (CC BY 4.0) άδεια. Τα πνευματικά δικαιώματα παραμένουν στους κατόχους των πρωτότυπων δικαιωμάτων πνευματικής ιδιοκτησίας όπως οι δημιουργοί ή τα ιδρύματά τους