Precisión mejorada para simulaciones de Trotter utilizando la interpolación de Chebyshev

Precisión mejorada para simulaciones de Trotter utilizando la interpolación de Chebyshev

Marca de tiempo: 26 de febrero de 2024 9:34 AM

Gumaro Rendón1, Jacob Watkins2y Nathan Wiebe3,4

1Zapata Computing Inc., Boston, MA 02110, EE. UU.
2Instalación para haces de isótopos raros, Universidad Estatal de Michigan, East Lansing, MI 48824, EE. UU.
3Departamento de Ciencias de la Computación, Universidad de Toronto, Toronto, ON M5S 2E4, Canadá
4Laboratorio Nacional del Noroeste del Pacífico, Richland, WA 99352, EE. UU.

¿Encuentra este documento interesante o quiere discutirlo? Scite o deje un comentario en SciRate.

Resumen

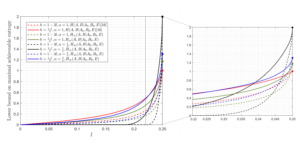
La metrología cuántica permite medir las propiedades de un sistema cuántico en el límite óptimo de Heisenberg. Sin embargo, cuando los estados cuánticos relevantes se preparan mediante simulación hamiltoniana digital, los errores algorítmicos acumulados provocarán desviaciones de este límite fundamental. En este trabajo, mostramos cómo los errores algorítmicos debidos a la evolución del tiempo trotterizado se pueden mitigar mediante el uso de técnicas estándar de interpolación polinomial. Nuestro enfoque consiste en extrapolar a cero el tamaño del paso de Trotter, similar a las técnicas de extrapolación sin ruido para mitigar los errores de hardware. Realizamos un análisis de error riguroso del enfoque de interpolación para estimar valores propios y valores esperados evolucionados en el tiempo, y mostramos que el límite de Heisenberg se logra hasta factores polilogarítmicos en el error. Nuestro trabajo sugiere que se pueden lograr precisiones cercanas a las de los algoritmos de simulación más modernos utilizando Trotter y recursos clásicos únicamente para una serie de tareas algorítmicas relevantes.

Precisión mejorada para simulaciones de Trotter utilizando la inteligencia de datos PlatoBlockchain de interpolación de Chebyshev. Búsqueda vertical. Ai.

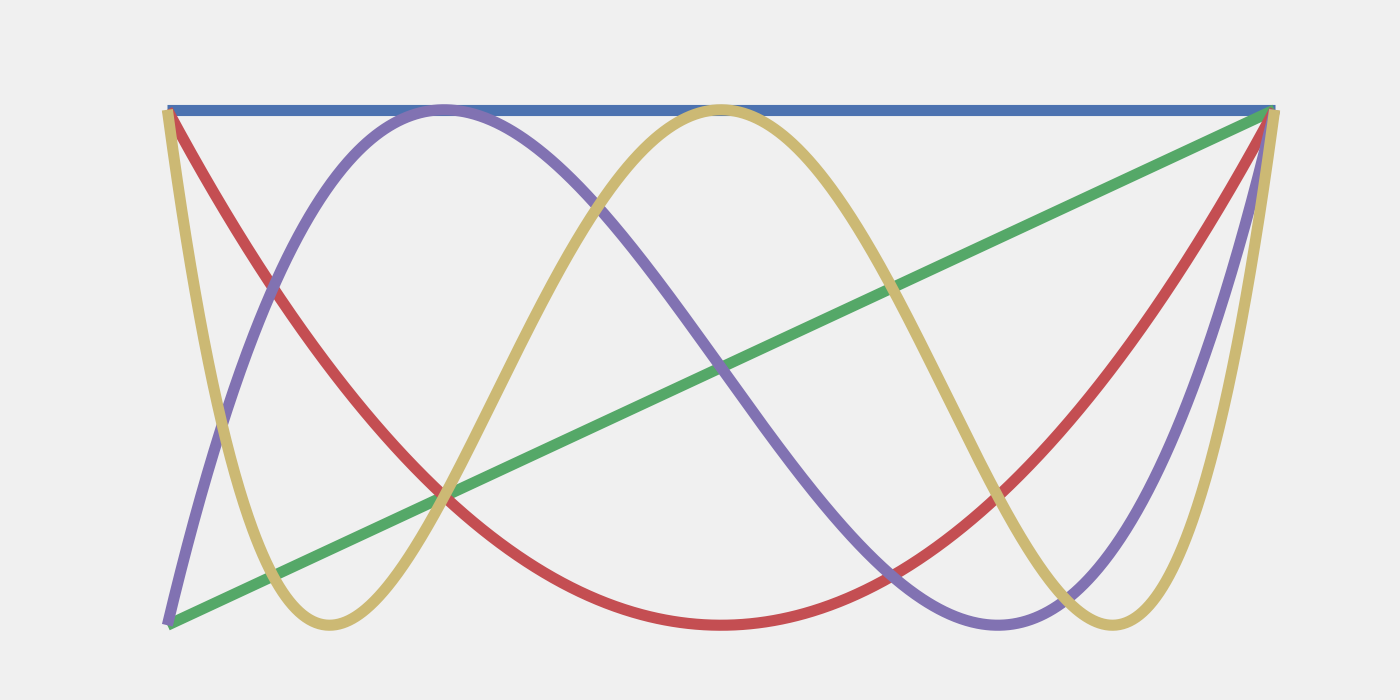
Imagen de portada: Los primeros cinco polinomios de Chebyshev. La interpolación en los ceros de Chebyshev sirve como un esquema sólido para la mitigación del error de Trotter.

[Contenido incrustado]

Resumen popular

Las computadoras cuánticas tienen el potencial de mejorar nuestra comprensión de la química, los materiales, la física nuclear y otras disciplinas científicas mediante una simulación cuántica mejorada. Hay varios algoritmos cuánticos disponibles para esta tarea y, entre ellos, las fórmulas de Trotter suelen ser las preferidas debido a su simplicidad y bajos costos iniciales. Desafortunadamente, las fórmulas de Trotter son, en teoría, relativamente inexactas en comparación con sus competidores más nuevos y sofisticados. Aunque un mayor tiempo de cálculo puede ayudar, esta estrategia rápidamente se vuelve inmanejable en los ruidosos dispositivos cuánticos de hoy en día, con una capacidad limitada para realizar cálculos largos e ininterrumpidos.

Para mitigar los errores en las simulaciones de Trotter sin aumentar el tiempo de procesamiento cuántico, utilizamos polinomios para conocer la relación entre el error y el tamaño del paso. Al recopilar datos para diferentes opciones de tamaño de paso, podemos interpolar, es decir, enhebrar, los datos con un polinomio y luego estimar el comportamiento esperado para tamaños de paso muy pequeños. Probamos matemáticamente que nuestro enfoque produce mejoras de precisión asintótica sobre el Trotter estándar para dos tareas fundamentales: estimar valores propios y estimar valores esperados.

Nuestro método es simple y práctico y solo requiere técnicas estándar en computación cuántica y clásica. Creemos que nuestro trabajo proporciona una sólida base teórica para futuras investigaciones sobre la mitigación de errores algorítmicos. Las extensiones de este trabajo podrían ocurrir en varias direcciones, desde eliminar suposiciones artificiales en nuestro análisis hasta demostrar simulaciones cuánticas mejoradas.

► datos BibTeX

► referencias

[ 1 ] S. Lloyd, Simuladores cuánticos universales, Science 273 (1996) 1073.
https: / / doi.org/ 10.1126 / science.273.5278.1073

[ 2 ] M. Reiher, N. Wiebe, KM Svore, D. Wecker y M. Troyer, Elucidando los mecanismos de reacción en computadoras cuánticas, Actas de la Academia Nacional de Ciencias 114 (2017) 7555.
https: / / doi.org/ 10.1073 / pnas.161915211

[ 3 ] JD Whitfield, J. Biamonte y A. Aspuru-Guzik, Simulación de estructuras electrónicas hamiltonianas utilizando computadoras cuánticas, Molecular Physics 109 (2011) 735.
https: / / doi.org/ 10.1080 / 00268976.2011.552441

[ 4 ] J. Lee, DW Berry, C. Gidney, WJ Huggins, JR McClean, N. Wiebe et al., Cálculos cuánticos de química aún más eficientes mediante hipercontracción tensorial, PRX Quantum 2 (2021) 030305.
https: / / doi.org/ 10.1103 / PRXQuantum.2.030305

[ 5 ] V. von Burg, GH Low, T. Häner, DS Steiger, M. Reiher, M. Roetteler et al., Computación cuántica catálisis computacional mejorada, Physical Review Research 3 (2021) 033055.
https: / / doi.org/ 10.1103 / PhysRevResearch.3.033055

[ 6 ] SP Jordan, KS Lee y J. Preskill, Algoritmos cuánticos para teorías cuánticas de campos, Science 336 (2012) 1130.
https: / / doi.org/ 10.1126 / science.1217069

[ 7 ] AF Shaw, P. Lougovski, JR Stryker y N. Wiebe, Algoritmos cuánticos para simular el modelo de red de Schwinger, Quantum 4 (2020) 306.
https:/​/​doi.org/​10.22331/​q-2020-08-10-306

[ 8 ] N. Klco, MJ Savage y JR Stryker, Su (2) teoría de campos de calibre no abeliano en una dimensión en computadoras cuánticas digitales, Physical Review D 101 (2020) 074512.
https: / / doi.org/ 10.1103 / PhysRevD.101.074512

[ 9 ] AM Childs y N. Wiebe, Simulación hamiltoniana utilizando combinaciones lineales de operaciones unitarias, Quantum Info. Computadora. 12 (2012) 901–924.
https: / / doi.org/ 10.26421 / QIC12.11-12-1

[ 10 ] GH Low, V. Kliuchnikov y N. Wiebe, Simulación hamiltoniana multiproducto bien condicionada, arXiv:1907.11679 (2019).
https://​/​doi.org/​10.48550/​arXiv.1907.11679
arXiv: 1907.11679

[ 11 ] DW Berry, AM Childs, R. Cleve, R. Kothari y RD Somma, Simulando la dinámica hamiltoniana con una serie de Taylor truncada, Physical review cards 114 (2015) 090502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.090502

[ 12 ] GH Low y N. Wiebe, Simulación hamiltoniana en la imagen de interacción, arXiv:1805.00675 (2018).
https://​/​doi.org/​10.48550/​arXiv.1805.00675
arXiv: 1805.00675

[ 13 ] M. Kieferová, A. Scherer y DW Berry, Simulando la dinámica de hamiltonianos dependientes del tiempo con una serie de Dyson truncada, Physical Review A 99 (2019) 042314.
https: / / doi.org/ 10.1103 / PhysRevA.99.042314

[ 14 ] GH Low e IL Chuang, Simulación hamiltoniana mediante qubitización, Quantum 3 (2019) 163.
https:/​/​doi.org/​10.22331/​q-2019-07-12-163

[ 15 ] R. Babbush, C. Gidney, DW Berry, N. Wiebe, J. McClean, A. Paler et al., Codificación de espectros electrónicos en circuitos cuánticos con complejidad t lineal, Physical Review X 8 (2018) 041015.
https: / / doi.org/ 10.1103 / PhysRevX.8.041015

[ 16 ] DW Berry, G. Ahokas, R. Cleve y BC Sanders, Algoritmos cuánticos eficientes para simular hamiltonianos dispersos, Communications in Mathematical Physics 270 (2006) 359–371.
https: / / doi.org/ 10.1007 / s00220-006-0150-x

[ 17 ] N. Wiebe, DW Berry, P. Høyer y BC Sanders, Simulación de la dinámica cuántica en una computadora cuántica, Journal of Physics A: Mathematical and Theoretical 44 (2011) 445308.
https:/​/​doi.org/​10.1088/​1751-8113/​44/​44/​445308

[ 18 ] AM Childs, Y. Su, MC Tran, N. Wiebe y S. Zhu, Teoría del error de trotón con escala del conmutador, Physical Review X 11 (2021) 011020.
https: / / doi.org/ 10.1103 / PhysRevX.11.011020

[ 19 ] J. Haah, MB Hastings, R. Kothari y GH Low, Algoritmo cuántico para simular la evolución en tiempo real de hamiltonianos reticulares, SIAM Journal on Computing (2021) FOCS18.
https: / / doi.org/ 10.1137 / 18M12315

[ 20 ] M. Hagan y N. Wiebe, Simulaciones cuánticas compuestas, arXiv:2206.06409 (2022).
https:/​/​doi.org/​10.22331/​q-2023-11-14-1181
arXiv: 2206.06409

[ 21 ] GH Low, Y. Su, Y. Tong y MC Tran, Sobre la complejidad de implementar pasos de trotón, arXiv:2211.09133 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.4.020323
arXiv: 2211.09133

[ 22 ] GH Low e IL Chuang, Simulación hamiltoniana óptima mediante procesamiento de señales cuánticas, Physical Review Letters 118 (2017).
https: / / doi.org/ 10.1103 / physrevlett.118.010501

[ 23 ] S. Endo, Q. Zhao, Y. Li, S. Benjamin y X. Yuan, Mitigación de errores algorítmicos en una simulación hamiltoniana, Phys. Rev. A 99 (2019) 012334.
https: / / doi.org/ 10.1103 / PhysRevA.99.012334

[ 24 ] AC Vazquez, R. Hiptmair y S. Woerner, Mejora del algoritmo de sistemas lineales cuánticos mediante la extrapolación de Richardson, ACM Transactions on Quantum Computing 3 (2022).
https: / / doi.org/ 10.1145 / 3490631

[ 25 ] AC Vazquez, DJ Egger, D. Ochsner y S. Woerner, Fórmulas multiproducto bien acondicionadas para una simulación hamiltoniana compatible con hardware, Quantum 7 (2023) 1067.
https:/​/​doi.org/​10.22331/​q-2023-07-25-1067

[ 26 ] M. Suzuki, Teoría general de integrales de trayectorias fractales con aplicaciones a teorías de muchos cuerpos y física estadística, Journal of Mathematical Physics 32 (1991) 400.
https: / / doi.org/ 10.1063 / 1.529425

[ 27 ] A. Gilyén, Y. Su, GH Low y N. Wiebe, Transformación cuántica de valores singulares y más allá: mejoras exponenciales para la aritmética de matrices cuánticas, en Actas del 51.º Simposio anual ACM SIGACT sobre teoría de la computación, págs. 193-204, 2019 , DOI.
https: / / doi.org/ 10.1145 / 3313276.3316366

[ 28 ] C. Yi y E. Crosson, Análisis espectral de fórmulas de productos para simulación cuántica, npj Quantum Information 8 (2022) 37.
https: / / doi.org/ 10.1038 / s41534-022-00548-w

[ 29 ] A. Quarteroni, R. Sacco y F. Saleri, Matemáticas numéricas, vol. 37, Springer Science & Business Media (2010), 10.1007/​b98885.
https: / / doi.org/ 10.1007 / b98885

[ 30 ] F. Piazzon y M. Vianello, Desigualdades de estabilidad para constantes de Lebesgue mediante desigualdades tipo Markov, Dolomites Research Notes on Approximation 11 (2018).

[ 31 ] AP de Camargo, Sobre la estabilidad numérica de la fórmula de Newton para la interpolación de Lagrange, Journal of Computational and Applied Mathematics 365 (2020) 112369.
https: / / doi.org/ 10.1016 / j.cam.2019.112369

[ 32 ] L. Trefethen, Seis mitos de la interpolación polinomial y la cuadratura, (2011).

[ 33 ] W. Gautschi, ¿Qué tan (ines)estables son los sistemas Vandermonde? análisis asintótico y computacional, en Lecture Notes in Pure and Applied Mathematics, págs. 193-210, Marcel Dekker, Inc, 1990.

[ 34 ] NJ Higham, La estabilidad numérica de la interpolación baricéntrica de Lagrange, IMA Journal of Numerical Analysis 24 (2004) 547.
https:/​/​doi.org/​10.1093/​imanum/​24.4.547

[ 35 ] JC Mason y DC Handscomb, polinomios de Chebyshev, CRC press (2002), 10.1201/​9781420036114.
https: / / doi.org/ 10.1201 / 9781420036114

[ 36 ] G. Rendon, T. Izubuchi e Y. Kikuchi, Efectos de la ventana de reducción gradual del coseno en la estimación de la fase cuántica, Physical Review D 106 (2022) 034503.
https: / / doi.org/ 10.1103 / PhysRevD.106.034503

[ 37 ] LN Trefethen, Teoría y práctica de la aproximación, edición ampliada, SIAM (2019), 10.1137/​1.9781611975949.
https: / / doi.org/ 10.1137 / 1.9781611975949

[ 38 ] FL Bauer y CT Fike, Normas y teoremas de exclusión, Numer. Matemáticas. 2 (1960) 137–141.
https: / / doi.org/ 10.1007 / BF01386217

[ 39 ] S. Blanes, F. Casas, J.-A. Oteo y J. Ros, La expansión magnus y algunas de sus aplicaciones, Informes de Física 470 (2009) 151.
https: / / doi.org/ 10.1016 / j.physrep.2008.11.001

[ 40 ] N. Klco y MJ Savage, Preparación de estados mínimamente entrelazados de funciones de onda localizadas en computadoras cuánticas, Physical Review A 102 (2020).
https: / / doi.org/ 10.1103 / physreva.102.012612

[ 41 ] JJ García-Ripoll, Algoritmos de inspiración cuántica para análisis multivariante: de la interpolación a las ecuaciones diferenciales parciales, Quantum 5 (2021) 431.
https:/​/​doi.org/​10.22331/​q-2021-04-15-431

[ 42 ] W. Górecki, R. Demkowicz-Dobrzański, HM Wiseman y DW Berry, Límite de Heisenberg corregido por $pi$, Cartas de revisión física 124 (2020) 030501.
https: / / doi.org/ 10.1103 / PhysRevLett.124.030501

[ 43 ] D. Grinko, J. Gacon, C. Zoufal y S. Woerner, Estimación iterativa de amplitud cuántica, npj Quantum Information 7 (2021) 52 [1912.05559].
https:/​/​doi.org/​10.1038/​s41534-021-00379-1
arXiv: 1912.05559

[ 44 ] N. Wiebe, D. Berry, P. Høyer y BC Sanders, Descomposiciones de orden superior de exponenciales de operadores ordenados, Journal of Physics A: Mathematical and Theoretical 43 (2010) 065203.
https:/​/​doi.org/​10.1088/​1751-8113/​43/​6/​065203

[ 45 ] RA Horn y CR Johnson, Análisis Matrix, Cambridge University Press (2012), 10.1017/​CBO9780511810817.
https: / / doi.org/ 10.1017 / CBO9780511810817

[ 46 ] M. Chiani, D. Dardari y MK Simon, Nuevos límites exponenciales y aproximaciones para el cálculo de la probabilidad de error en canales con desvanecimiento, IEEE Transactions on Wireless Communications 2 (2003) 840.
https://​/​doi.org/​10.1109/​TWC.2003.814350

[ 47 ] JM Borwein y PB Borwein, Pi y la AGM: un estudio sobre la teoría analítica de números y la complejidad computacional, Wiley-Interscience (1987).

[ 48 ] BL Higgins, DW Berry, SD Bartlett, HM Wiseman y GJ Pryde, Estimación de fase limitada de Heisenberg sin entrelazamiento, Nature 450 (2007) 393.
https: / / doi.org/ 10.1038 / nature06257

[ 49 ] RB Griffiths y C.-S. Niu, Transformada semiclásica de Fourier para computación cuántica, Physical Review Letters 76 (1996) 3228.
https: / / doi.org/ 10.1103 / PhysRevLett.76.3228

[ 50 ] AY Kitaev, Medidas cuánticas y el problema del estabilizador abeliano, quant-ph/​9511026 (1995).
https:/​/​doi.org/​10.48550/​arXiv.quant-ph/​9511026
arXiv: quant-ph / 9511026

[ 51 ] DS Abrams y S. Lloyd, Algoritmo cuántico que proporciona un aumento de velocidad exponencial para encontrar valores propios y vectores propios, Physical Review Letters 83 (1999) 5162.
https: / / doi.org/ 10.1103 / PhysRevLett.83.5162

[ 52 ] J. Watkins, N. Wiebe, A. Roggero y D. Lee, Simulación hamiltoniana dependiente del tiempo utilizando construcciones de relojes discretos, arXiv:2203.11353 (2022).
https://​/​doi.org/​10.48550/​arXiv.2203.11353
arXiv: 2203.11353

[ 53 ] TD Ahle, Límites nítidos y simples para los momentos brutos de las distribuciones binomial y de Poisson, Statistics & Probability Letters 182 (2022) 109306.
https://​/​doi.org/​10.1016/​j.spl.2021.109306

[ 54 ] T. Rivlin, Polinomios de Chebyshev, Dover Books on Mathematics, Dover Publications (2020).

Citado por

[1] Dean Lee, "Técnicas cuánticas para problemas de valores propios", Revista Física Europea A 59 11, 275 (2023).

[2] Tatsuhiko N. Ikeda, Hideki Kono y Keisuke Fujii, "Trotter24: una trotterización de tamaño escalonado adaptativa con precisión garantizada para simulaciones hamiltonianas", arXiv: 2307.05406, (2023).

[3] Hans Hon Sang Chan, Richard Meister, Matthew L. Goh y Bálint Koczor, “Espectroscopía algorítmica de sombras”, arXiv: 2212.11036, (2022).

[4] Sergiy Zhuk, Niall Robertson y Sergey Bravyi, "Límites de error de trotón y fórmulas dinámicas de productos múltiples para la simulación hamiltoniana", arXiv: 2306.12569, (2023).

[5] Zhicheng Zhang, Qisheng Wang y Mingsheng Ying, “Algoritmo cuántico paralelo para simulación hamiltoniana”, Cuántica 8, 1228 (2024).

[6] Lea M. Trenkwalder, Eleanor Scerri, Thomas E. O'Brien y Vedran Dunjko, “Compilación de simulación hamiltoniana de fórmula de producto mediante aprendizaje por refuerzo”, arXiv: 2311.04285, (2023).

[7] Gumaro Rendón y Peter D. Johnson, “Estimación de energía del estado gaussiano de baja profundidad”, arXiv: 2309.16790, (2023).

[8] Gregory Boyd, “Paralelización de LCU con bajos gastos generales a través de operadores de conmutación”, arXiv: 2312.00696, (2023).

Las citas anteriores son de ANUNCIOS SAO / NASA (última actualización exitosa 2024-02-27 02:40:25). La lista puede estar incompleta ya que no todos los editores proporcionan datos de citas adecuados y completos.

On Servicio citado por Crossref no se encontraron datos sobre las obras citadas (último intento 2024-02-27 02:40:24).

Este documento se publica en Quantum bajo el Creative Commons Reconocimiento 4.0 Internacional (CC BY 4.0) licencia. Los derechos de autor permanecen con los titulares de derechos de autor originales, como los autores o sus instituciones.

Sello de tiempo:

Mas de Diario cuántico