Redes de calibre cuántico: un nuevo tipo de red tensorial

Redes de calibre cuántico: un nuevo tipo de red tensorial

Sello de tiempo: 14 de septiembre de 2023 11:33 a.m.

kevin escoria

Departamento de Ingeniería Eléctrica e Informática, Rice University, Houston, Texas 77005 EE. UU.
Departamento de Física, Instituto de Tecnología de California, Pasadena, California 91125, EE. UU.
Instituto de Información y Materia Cuántica e Instituto Walter Burke de Física Teórica, Instituto de Tecnología de California, Pasadena, California 91125, EE. UU.

¿Encuentra este documento interesante o quiere discutirlo? Scite o deje un comentario en SciRate.

Resumen

Aunque las redes tensoriales son herramientas poderosas para simular la física cuántica de baja dimensión, los algoritmos de redes tensoriales son muy costosos desde el punto de vista computacional en dimensiones espaciales superiores. Presentamos $textit{redes de calibre cuántico}$: un tipo diferente de ansatz de red tensorial para el cual el costo de cálculo de las simulaciones no aumenta explícitamente para dimensiones espaciales más grandes. Nos inspiramos en la imagen de calibre de la dinámica cuántica, que consiste en una función de onda local para cada zona del espacio, con zonas vecinas relacionadas mediante conexiones unitarias. Una red de calibre cuántico (QGN) tiene una estructura similar, excepto que las dimensiones del espacio de Hilbert de las funciones de onda locales y las conexiones están truncadas. Describimos cómo se puede obtener un QGN a partir de una función de onda genérica o un estado de producto matricial (MPS). Todas las funciones de correlación de $2k$ puntos de cualquier función de onda para $M$ muchos operadores pueden codificarse exactamente mediante un QGN con dimensión de enlace $O(M^k)$. En comparación, por solo $ k = 1 $, generalmente se requiere una dimensión de enlace exponencialmente mayor de $ 2 ^ {M/6} $ para un MPS de qubits. Proporcionamos un algoritmo QGN simple para simulaciones aproximadas de dinámica cuántica en cualquier dimensión espacial. La dinámica aproximada puede lograr una conservación de energía exacta para los hamiltonianos independientes del tiempo, y las simetrías espaciales también pueden mantenerse exactamente. Comparamos el algoritmo simulando la extinción cuántica de hamiltonianos fermiónicos en hasta tres dimensiones espaciales.

Redes de calibre cuántico: un nuevo tipo de inteligencia de datos PlatoBlockchain de red tensorial. Búsqueda vertical. Ai.

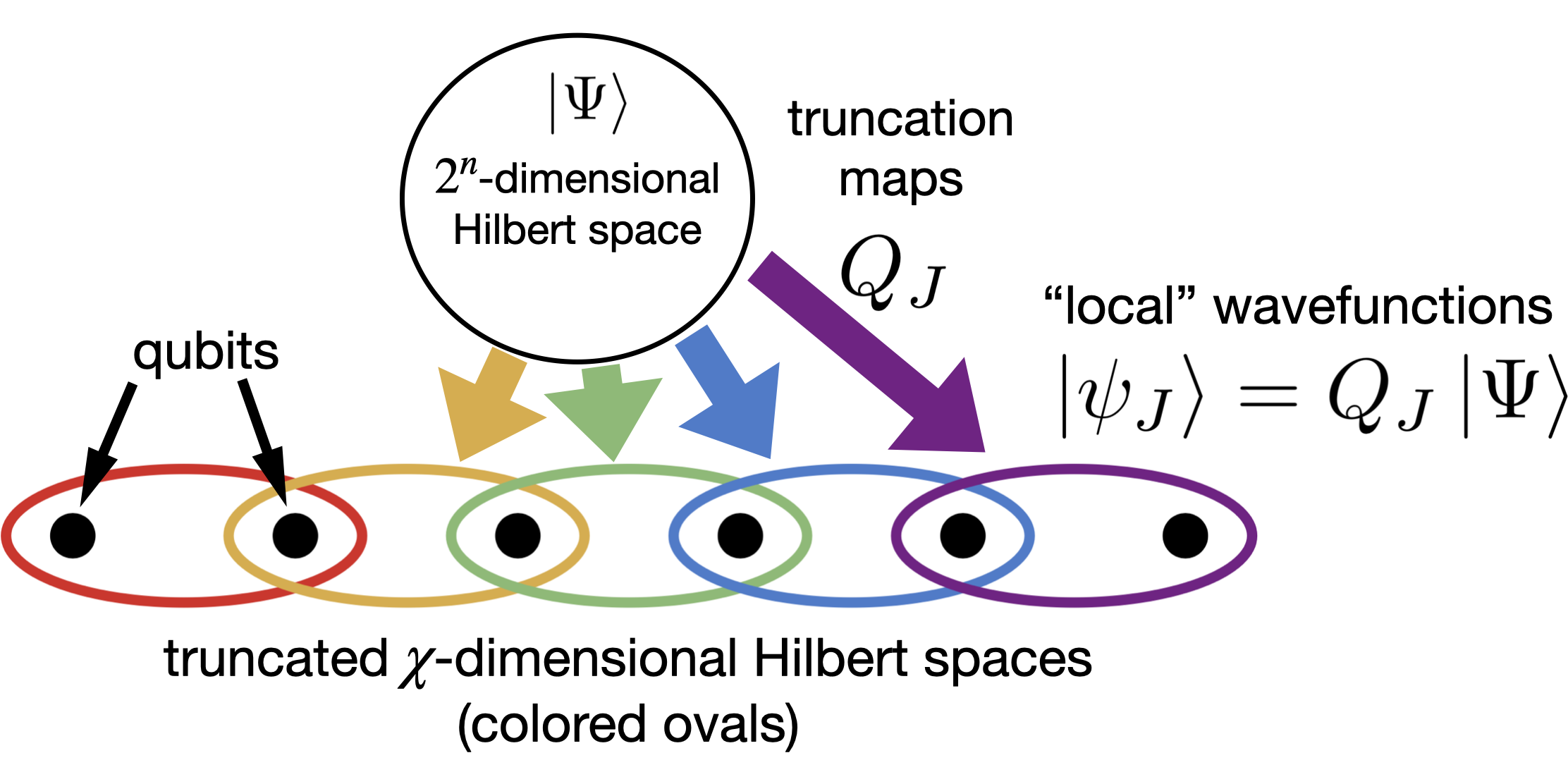
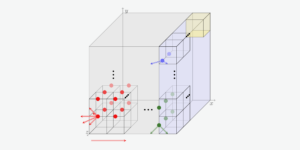
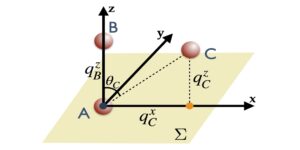
Imagen de portada: En la imagen de calibre, diferentes zonas del espacio (óvalos en la figura) están asociadas con sus propios espacios de Hilbert y funciones de onda, que están relacionados mediante transformaciones unitarias que evolucionan en el tiempo. Cada uno de estos espacios de Hilbert tiene la dimensión habitual de $2^n$ para un sistema de $n$ qubits. Las redes de calibre cuántico aprovechan estos múltiples espacios de Hilbert truncando eficientemente cada espacio de Hilbert en un subespacio de estados más pequeño que es más relevante para la física local del parche asociado utilizando un mapa de truncamiento lineal.

[Contenido incrustado]

Resumen popular

La simulación de sistemas cuánticos de muchas partículas o de muchos qubits es exigente desde el punto de vista computacional debido al crecimiento exponencial de la dimensión del espacio de Hilbert con el número de partículas o qubits. Una clase de ansatz de función de onda conocida como "redes tensoriales" puede parametrizar eficientemente estos enormes espacios de Hilbert mediante una contracción de una cuadrícula de tensores. Si bien han demostrado un éxito notable en una dimensión espacial (mediante, por ejemplo, el algoritmo "DMRG"), los algoritmos de redes tensoriales son menos eficientes y más complicados en dos o más dimensiones espaciales.

Nuestro trabajo inicia el estudio de una nueva función de función de onda denominada "red de calibre cuántico". Mostramos que las redes de calibre cuántico están relacionadas con las redes tensoriales en una dimensión espacial, pero son algorítmicamente más simples y potencialmente más eficientes en dos o más dimensiones espaciales. Las redes de calibre cuántico utilizan una nueva imagen de la mecánica cuántica, denominada "imagen de calibre", que se describe brevemente en la imagen presentada. Proporcionamos un algoritmo simple para simular aproximadamente la evolución temporal de una función de onda utilizando una red de calibre cuántico. Comparamos el algoritmo con un sistema de fermiones en hasta tres dimensiones espaciales. Simular el sistema tridimensional utilizando redes tensoriales sería un gran desafío. Sin embargo, se necesita más investigación para comprender mejor la teoría de la red de calibre cuántico y desarrollar más algoritmos, como un algoritmo de optimización del estado fundamental.

► datos BibTeX

► referencias

[ 1 ] Kevin Slagle. “La imagen de calibre de la dinámica cuántica” (2022). arXiv:2210.09314.
arXiv: 2210.09314

[ 2 ] Román Orús. “Redes tensoriales para sistemas cuánticos complejos”. Nature Reviews Physics 1, 538–550 (2019). arXiv:1812.04011.
https:/​/​doi.org/​10.1038/​s42254-019-0086-7
arXiv: 1812.04011

[ 3 ] Román Orús. "Una introducción práctica a las redes tensoriales: estados de productos matriciales y estados de pares entrelazados proyectados". Anales de Física 349, 117-158 (2014). arXiv:1306.2164.
https: / / doi.org/ 10.1016 / j.aop.2014.06.013
arXiv: 1306.2164

[ 4 ] Garnet Kin-Lic Chan, Anna Keselman, Naoki Nakatani, Zhendong Li y Steven R. White. “Operadores de productos matriciales, estados de productos matriciales y algoritmos ab initio del grupo de renormalización de matrices de densidad” (2016). arXiv:1605.02611.
arXiv: 1605.02611

[ 5 ] Ignacio Cirac, David Pérez-García, Norbert Schuch y Frank Verstraete. “Estados del producto matricial y estados de pares entrelazados proyectados: conceptos, simetrías y teoremas” (2020). arXiv:2011.12127.
https: / / doi.org/ 10.1103 / RevModPhys.93.045003
arXiv: 2011.12127

[ 6 ] Shi-Ju Ran, Emanuele Tirrito, Cheng Peng, Xi Chen, Luca Tagliacozzo, Gang Su y Maciej Lewenstein. “Contracciones de la red tensorial” (2020). arXiv:1708.09213.
https:/​/​doi.org/​10.1007/​978-3-030-34489-4
arXiv: 1708.09213

[ 7 ] Jacob C. Bridgeman y Christopher T. Chubb. “Agitación de manos y danza interpretativa: un curso de introducción a las redes tensoriales”. Revista de Física A Matemática General 50, 223001 (2017). arXiv:1603.03039.
https:/​/​doi.org/​10.1088/​1751-8121/​aa6dc3
arXiv: 1603.03039

[ 8 ] Michael P. Zaletel y Frank Pollmann. “Estados de redes tensoriales isométricas en dos dimensiones”. Física. Rev. Lett. 124, 037201 (2020). arXiv:1902.05100.
https: / / doi.org/ 10.1103 / PhysRevLett.124.037201
arXiv: 1902.05100

[ 9 ] Katharine Hyatt y EM Stoudenmire. “Enfoque DMRG para optimizar redes tensoriales bidimensionales” (2019). arXiv:1908.08833.
arXiv: 1908.08833

[ 10 ] Reza Haghshenas, Matthew J. O'Rourke y Garnet Kin-Lic Chan. "Conversión de estados de pares entrelazados proyectados a una forma canónica". Física. Rev. B 100, 054404 (2019). arXiv:1903.03843.
https: / / doi.org/ 10.1103 / PhysRevB.100.054404
arXiv: 1903.03843

[ 11 ] Maurits SJ Tepaske y David J. Luitz. “Redes tensoriales isométricas tridimensionales”. Investigación de revisión física 3, 023236 (2021). arXiv:2005.13592.
https: / / doi.org/ 10.1103 / PhysRevResearch.3.023236
arXiv: 2005.13592

[ 12 ] G. Vidal. "Clase de estados cuánticos de muchos cuerpos que pueden simularse de manera eficiente". Física. Rev. Lett. 101, 110501 (2008). arXiv:quant-ph/​0610099.
https: / / doi.org/ 10.1103 / PhysRevLett.101.110501
arXiv: quant-ph / 0610099

[ 13 ] G. Evenbly y G. Vidal. "Clase de estados de muchos cuerpos altamente entrelazados que pueden simularse de manera eficiente". Física. Rev. Lett. 112, 240502 (2014). arXiv:1210.1895.
https: / / doi.org/ 10.1103 / PhysRevLett.112.240502
arXiv: 1210.1895

[ 14 ] G. Evenbly y G. Vidal. “Algoritmos para la renormalización del entrelazamiento”. Física. Rev. B 79, 144108 (2009). arXiv:0707.1454.
https: / / doi.org/ 10.1103 / PhysRevB.79.144108
arXiv: 0707.1454

[ 15 ] Arturo Acuaviva, Visu Makam, Harold Nieuwboer, David Pérez-García, Friedrich Sittner, Michael Walter y Freek Witteveen. “La forma canónica mínima de una red tensorial” (2022). arXiv:2209.14358.
arXiv: 2209.14358

[ 16 ] Giovanni Ferrari, Giuseppe Magnífico y Simone Montangero. "Redes de tensores de árboles ponderados adaptativamente para sistemas cuánticos desordenados de muchos cuerpos". Física. Rev. B 105, 214201 (2022). arXiv:2111.12398.
https: / / doi.org/ 10.1103 / PhysRevB.105.214201
arXiv: 2111.12398

[ 17 ] La dinámica temporal de un fermión libre hamiltoniano $hat{H} = sum_{ij} h_{ij} hat{c}_i^dagger hat{c}_j$ se puede simular exactamente calculando las funciones de onda de un solo fermión llenas evolucionadas en el tiempo. $|{phi_alpha(t)rangle} = e^{-iht} |{phi_alpha(0)rangle}$. La función de onda $|{Psi}rangle = prod_alpha^text{filled} big(sum_i langle{i|phi_alpha}rangle hat{c}_i^daggerbig) |{0}rangle$ nunca se calcula explícitamente. $prod_alpha^text{filled}$ denota el producto sobre las funciones de onda de un solo fermión llenas y $|{0}rangle$ es el estado vacío sin fermiones. Entonces $langle{hat{n}_i(t)}rangle = sum_alpha^text{filled} |langle{i|phi_alpha(t)rangle}|^2$, donde $|{i}rangle$ es el fermión único Función de onda para un fermión en el sitio $i$.

[ 18 ] Román Orús. “Avances en la teoría de redes tensoriales: simetrías, fermiones, entrelazamiento y holografía”. Revista Física Europea B 87, 280 (2014). arXiv:1407.6552.
https: / / doi.org/ 10.1140 / epjb / e2014-50502-9
arXiv: 1407.6552

[ 19 ] Philippe Corboz y Guifré Vidal. “Ansatz de renormalización de entrelazamiento multiescala fermiónico”. Física. Rev. B 80, 165129 (2009). arXiv:0907.3184.
https: / / doi.org/ 10.1103 / PhysRevB.80.165129
arXiv: 0907.3184

[ 20 ] Andrew M. Childs, Yuan Su, Minh C. Tran, Nathan Wiebe y Shuchen Zhu. “Teoría del error de trotón con escalado del conmutador”. Física. Rev. X 11, 011020 (2021). arXiv:1912.08854.
https: / / doi.org/ 10.1103 / PhysRevX.11.011020
arXiv: 1912.08854

[ 21 ] Bram Vanhecke, Laurens Vanderstraeten y Frank Verstraete. “Expansiones de clústeres simétricos con redes tensoriales” (2019). arXiv:1912.10512.
https: / / doi.org/ 10.1103 / PhysRevA.103.L020402
arXiv: 1912.10512

[ 22 ] Yi Kai Liu. "La consistencia de las matrices de densidad local es qma-completa". En Josep Díaz, Klaus Jansen, José DP Rolim y Uri Zwick, editores, Aproximación, aleatorización y optimización combinatoria. Algoritmos y Técnicas. Páginas 438–449. Berlín, Heidelberg (2006). Springer Berlín Heidelberg. arXiv:quant-ph/​0604166.
arXiv: quant-ph / 0604166

[ 23 ] Alexander A. Klyachko. “Problema marginal cuántico y N-representabilidad”. En Serie de conferencias del Journal of Physics. Volumen 36 de la serie de conferencias Journal of Physics, páginas 72–86. (2006). arXiv:quant-ph/​0511102.
https:/​/​doi.org/​10.1088/​1742-6596/​36/​1/​014
arXiv: quant-ph / 0511102

[ 24 ] Jianxin Chen, Zhengfeng Ji, Nengkun Yu y Bei Zeng. "Detección de coherencia de marginales cuánticos superpuestos mediante separabilidad". Física. Rev. A 93, 032105 (2016). arXiv:1509.06591.
https: / / doi.org/ 10.1103 / PhysRevA.93.032105
arXiv: 1509.06591

[ 25 ] David A. Mazziotti. “Estructura de matrices de densidad fermiónica: condiciones completas de representabilidad $n$”. Física. Rev. Lett. 108, 263002 (2012). arXiv:1112.5866.
https: / / doi.org/ 10.1103 / PhysRevLett.108.263002
arXiv: 1112.5866

[ 26 ] Xiao-Gang Wen. “Coloquio: Zoológico de fases topológicas cuánticas de la materia”. Reseñas de Física Moderna 89, 041004 (2017). arXiv:1610.03911.
https: / / doi.org/ 10.1103 / RevModPhys.89.041004
arXiv: 1610.03911

[ 27 ] Zheng-Cheng Gu, Michael Levin, Brian Swingle y Xiao-Gang Wen. "Representaciones de productos tensoriales para estados condensados ​​de redes de cadenas". Física. Rev. B 79, 085118 (2009). arXiv:0809.2821.
https: / / doi.org/ 10.1103 / PhysRevB.79.085118
arXiv: 0809.2821

[ 28 ] Oliver Buerschaper, Miguel Aguado y Guifré Vidal. "Representación explícita de redes tensoriales para los estados fundamentales de modelos de redes de cuerdas". Física. Rev. B 79, 085119 (2009). arXiv:0809.2393.
https: / / doi.org/ 10.1103 / PhysRevB.79.085119
arXiv: 0809.2393

[ 29 ] Dominic J. Williamson, Nick Bultinck y Frank Verstraete. “Orden topológico enriquecido con simetría en redes tensoriales: defectos, calibres y condensación cualquiera” (2017). arXiv:1711.07982.
arXiv: 1711.07982

[ 30 ] Tomohiro Soejima, Karthik Siva, Nick Bultinck, Shubhayu Chatterjee, Frank Pollmann y Michael P. Zaletel. "Representación de red tensorial isométrica de líquidos en red de cuerdas". Física. Rev. B 101, 085117 (2020). arXiv:1908.07545.
https: / / doi.org/ 10.1103 / PhysRevB.101.085117
arXiv: 1908.07545

[ 31 ] Guifre Vidal. “Simulación eficiente de sistemas cuánticos de muchos cuerpos unidimensionales”. Física. Rev. Lett. 93, 040502 (2004). arXiv:quant-ph/​0310089.
https: / / doi.org/ 10.1103 / PhysRevLett.93.040502
arXiv: quant-ph / 0310089

[ 32 ] Sebastian Paeckel, Thomas Köhler, Andreas Swoboda, Salvatore R. Manmana, Ulrich Schollwöck y Claudius Hubig. “Métodos de evolución temporal para estados matriz-producto”. Anales de Física 411, 167998 (2019). arXiv:1901.05824.
https: / / doi.org/ 10.1016 / j.aop.2019.167998
arXiv: 1901.05824

[ 33 ] Steven R. White y Adrian E. Feiguin. “Evolución en tiempo real utilizando el grupo de renormalización de la matriz de densidad”. Física. Rev. Lett. 93, 076401 (2004). arXiv:cond-mat/​0403310.
https: / / doi.org/ 10.1103 / PhysRevLett.93.076401
arXiv: cond-mat / 0403310

[ 34 ] Jutho Haegeman, Christian Lubich, Ivan Oseledets, Bart Vandereycken y Frank Verstraete. “Unificando la evolución y optimización del tiempo con los estados matriciales del producto”. Física. Rev.B 94, 165116 (2016). arXiv:1408.5056.
https: / / doi.org/ 10.1103 / PhysRevB.94.165116
arXiv: 1408.5056

[ 35 ] Eyal Leviatan, Frank Pollmann, Jens H. Bardarson, David A. Huse y Ehud Altman. “Dinámica de termalización cuántica con estados matriz-producto” (2017). arXiv:1702.08894.
arXiv: 1702.08894

[ 36 ] Christian B. Mendl. “Evolución temporal de operadores de productos matriciales con conservación de energía” (2018). arXiv:1812.11876.
arXiv: 1812.11876

[ 37 ] Piotr Czarnik, Jacek Dziarmaga y Philippe Corboz. “Evolución temporal de un estado de par entrelazado proyectado infinito: un algoritmo eficiente”. Física. Rev. B 99, 035115 (2019). arXiv:1811.05497.
https: / / doi.org/ 10.1103 / PhysRevB.99.035115
arXiv: 1811.05497

[ 38 ] Daniel Bauernfeind y Markus Aichhorn. "Principio variacional dependiente del tiempo para redes tensoriales de árboles". SciPost Física 8, 024 (2020). arXiv:1908.03090.
https: / / doi.org/ 10.21468 / SciPostPhys.8.2.024
arXiv: 1908.03090

[ 39 ] Christopher David White, Michael Zaletel, Roger SK Mong y Gil Refael. “Dinámica cuántica de sistemas termalizadores”. Física. Rev. B 97, 035127 (2018). arXiv:1707.01506.
https: / / doi.org/ 10.1103 / PhysRevB.97.035127
arXiv: 1707.01506

[ 40 ] Tibor Rakovszky, CW von Keyserlingk y Frank Pollmann. “Método de evolución de operadores asistidos por disipación para capturar transporte hidrodinámico”. Física. Rev. B 105, 075131 (2022). arXiv:2004.05177.
https: / / doi.org/ 10.1103 / PhysRevB.105.075131
arXiv: 2004.05177

[ 41 ] Mingru Yang y Steven R. White. "Principio variacional dependiente del tiempo con subespacio auxiliar de Krylov". Física. Rev. B 102, 094315 (2020). arXiv:2005.06104.
https: / / doi.org/ 10.1103 / PhysRevB.102.094315
arXiv: 2005.06104

[ 42 ] Benedikt Kloss, David Reichman y Yevgeny Bar Lev. “Estudiar la dinámica en redes cuánticas bidimensionales utilizando estados de redes tensoriales de árboles”. SciPost Física 9, 070 (2020). arXiv:2003.08944.
https: / / doi.org/ 10.21468 / SciPostPhys.9.5.070
arXiv: 2003.08944

[ 43 ] Álvaro M. Alhambra y J. Ignacio Cirac. “Redes tensoriales localmente precisas para estados térmicos y evolución del tiempo”. PRX Quantum 2, 040331 (2021). arXiv:2106.00710.
https: / / doi.org/ 10.1103 / PRXQuantum.2.040331
arXiv: 2106.00710

[ 44 ] Sheng-Hsuan Lin, Michael Zaletel y Frank Pollmann. “Simulación eficiente de la dinámica en sistemas de espín cuántico bidimensionales con redes tensoriales isométricas” (2021). arXiv:2112.08394.
https: / / doi.org/ 10.1103 / PhysRevB.106.245102
arXiv: 2112.08394

[ 45 ] Markus Schmitt y Markus Heyl. “Dinámica cuántica de muchos cuerpos en dos dimensiones con redes neuronales artificiales”. Física. Rev. Lett. 125, 100503 (2020). arXiv:1912.08828.
https: / / doi.org/ 10.1103 / PhysRevLett.125.100503
arXiv: 1912.08828

[ 46 ] Irene López Gutiérrez y Christian B. Mendl. "Evolución en tiempo real con estados cuánticos de redes neuronales". Cuántico 6, 627 (2022). arXiv:1912.08831.
https:/​/​doi.org/​10.22331/​q-2022-01-20-627
arXiv: 1912.08831

[ 47 ] Sheng-Hsuan Lin y Frank Pollmann. "Escalado de estados cuánticos de redes neuronales para la evolución del tiempo". Estado físico Solidi B Investigación básica 259, 2100172 (2022). arXiv:2104.10696.
https://​/​doi.org/​10.1002/​pssb.202100172
arXiv: 2104.10696

[ 48 ] Dariia Yehorova y Joshua S. Kretchmer. “Una extensión de múltiples fragmentos en tiempo real de la teoría de incrustación de matriz de densidad proyectada: dinámica de electrones en desequilibrio en sistemas extendidos” (2022). arXiv:2209.06368.
https: / / doi.org/ 10.1063 / 5.0146973
arXiv: 2209.06368

[ 49 ] G. Münster y M. Walzl. “Teoría del calibre de celosía: breve introducción” (2000). arXiv:hep-lat/​0012005.
arXiv:hep-lat/0012005

[ 50 ] Juan B. Kogut. “Una introducción a la teoría de calibre de celosía y sistemas de espín”. Rev.Mod. física 51, 659–713 (1979).
https: / / doi.org/ 10.1103 / RevModPhys.51.659

[ 51 ] Kevin Slagle y John Preskill. “Mecánica cuántica emergente en el límite de un modelo de red clásico local” (2022). arXiv:2207.09465.
https: / / doi.org/ 10.1103 / PhysRevA.108.012217
arXiv: 2207.09465

[ 52 ] Scott Aaronson. “Fórmulas multilineales y escepticismo de la computación cuántica”. En actas del trigésimo sexto simposio anual ACM sobre teoría de la informática. Páginas 118–127. STOC '04Nueva York, NY, Estados Unidos (2004). Asociación para Maquinaria de Computación. arXiv:quant-ph/​0311039.
https: / / doi.org/ 10.1145 / 1007352.1007378
arXiv: quant-ph / 0311039

[ 53 ] Gerard't Hooft. “Mecánica cuántica determinista: las ecuaciones matemáticas” (2020). arXiv:2005.06374.
arXiv: 2005.06374

[ 54 ] Stephen L Adler. “La teoría cuántica como fenómeno emergente: fundamentos y fenomenología”. Revista de Física: Serie de conferencias 361, 012002 (2012).
https:/​/​doi.org/​10.1088/​1742-6596/​361/​1/​012002

[ 55 ] Vitali Vanchurin. “Mecánica entrópica: hacia una descripción estocástica de la mecánica cuántica”. Fundamentos de la Física 50, 40–53 (2019). arXiv:1901.07369.
https:/​/​doi.org/​10.1007/​s10701-019-00315-6
arXiv: 1901.07369

[ 56 ] Eduardo Nelson. “Revisión de la mecánica estocástica”. Revista de Física: Serie de conferencias 361, 012011 (2012).
https:/​/​doi.org/​10.1088/​1742-6596/​361/​1/​012011

[ 57 ] Michael JW Hall, Dirk-André Deckert y Howard M. Wiseman. "Fenómenos cuánticos modelados por interacciones entre muchos mundos clásicos". Revisión física X 4, 041013 (2014). arXiv:1402.6144.
https: / / doi.org/ 10.1103 / PhysRevX.4.041013
arXiv: 1402.6144

[ 58 ] Guifre Vidal. “Simulación clásica eficiente de cálculos cuánticos ligeramente entrelazados”. Física. Rev. Lett. 91, 147902 (2003). arXiv:quant-ph/​0301063.
https: / / doi.org/ 10.1103 / PhysRevLett.91.147902
arXiv: quant-ph / 0301063

[ 59 ] G. Vidal. “Simulación clásica de sistemas de celosía cuántica de tamaño infinito en una dimensión espacial”. Física. Rev. Lett. 98, 070201 (2007). arXiv:cond-mat/​0605597.
https: / / doi.org/ 10.1103 / PhysRevLett.98.070201
arXiv: cond-mat / 0605597

[ 60 ] Stephan Ramón García, Matthew Okubo Patterson y William T. Ross. “Matrices parcialmente isométricas: una encuesta breve y selectiva” (2019). arXiv:1903.11648.
arXiv: 1903.11648

[ 61 ] CJ Hamer. “Escalado de tamaño finito en el modelo transversal de Ising sobre una red cuadrada”. Revista de Física Un General Matemático 33, 6683–6698 (2000). arXiv:cond-mat/​0007063.
https:/​/​doi.org/​10.1088/​0305-4470/​33/​38/​303
arXiv: cond-mat / 0007063

Citado por

[1] Sayak Guha Roy y Kevin Slagle, "Interpolación entre las imágenes de dinámica cuántica de Gauge y Schrödinger", arXiv: 2307.02369, (2023).

[2] Kevin Slagle, "La imagen de calibre de la dinámica cuántica", arXiv: 2210.09314, (2022).

Las citas anteriores son de ANUNCIOS SAO / NASA (última actualización exitosa 2023-09-15 05:31:41). La lista puede estar incompleta ya que no todos los editores proporcionan datos de citas adecuados y completos.

On Servicio citado por Crossref no se encontraron datos sobre las obras citadas (último intento 2023-09-15 05:31:39).

Este documento se publica en Quantum bajo el Creative Commons Reconocimiento 4.0 Internacional (CC BY 4.0) licencia. Los derechos de autor permanecen con los titulares de derechos de autor originales, como los autores o sus instituciones.

Sello de tiempo:

Mas de Diario cuántico