El modelo de mezcla de procesos de Dirichlet

• Sábado, Junio 23, 2014
• Vasilis Vryniotis
• . 2 comentarios

Esta publicación de blog es la cuarta parte de la serie sobre Agrupación con modelos de mezcla de procesos Dirichlet. En artículos anteriores discutimos los modelos finitos de mezcla de Dirichlet y tomamos el límite de su modelo para infinitos grupos de k que nos llevaron a la introducción de procesos de Dirichlet. Como vimos, nuestro objetivo es construir un modelo de mezcla que no requiera que especifiquemos el número de k grupos / componentes desde el principio. Después presentando diferentes representaciones de procesos de Dirichlet, ahora es el momento de utilizar realmente los DP para construir un modelo de mezcla infinito que nos permita realizar la agrupación. El objetivo de este artículo es definir los modelos de mezcla de procesos de Dirichlet y analizar el uso del proceso de restaurantes chinos y el muestreo de Gibbs. Si no ha leído las publicaciones anteriores, se recomienda hacerlo, ya que el tema es un poco teórico y requiere una buena comprensión de la construcción del modelo.

Actualización: el marco de aprendizaje automático de Datumbox ahora es de código abierto y gratuito para descargar. Consulte el paquete com.datumbox.framework.machinelearning.clustering para ver la implementación de los modelos de mezcla de procesos de Dirichlet en Java.

1. Definición del modelo de mezcla de proceso de Dirichlet

El uso de Procesos de Dirichlet nos permite tener un modelo de mezcla con componentes infinitos que puede considerarse que lleva el límite del modelo finito de k al infinito. Supongamos que tenemos el siguiente modelo:

Ecuación 1: Modelo de mezcla de proceso de Dirichlet

Donde G se define como y utilizado como una notación corta para que es una función delta que toma 1 si y 0 en otra parte. El θ_i son los parámetros del grupo que se muestrean de G. La distribución generativa F se configura mediante los parámetros del grupo θ_i y se usa para generar x_i observaciones Finalmente podemos definir una distribución de densidad que es nuestra distribución de mezcla (mezcla infinita contable) con proporciones de mezcla y componentes de mezcla .

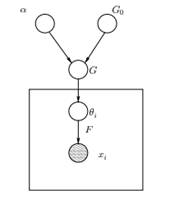
Figura 1: Modelo gráfico del modelo de mezcla de proceso de Dirichlet

Arriba podemos ver el modelo gráfico equivalente del DPMM. El g₀ es la distribución base de DP y generalmente se selecciona para ser conjugada antes de nuestra distribución generativa F para facilitar los cálculos y hacer uso de las atractivas propiedades matemáticas. El α es el hiperparámetro escalar del Proceso de Dirichlet y afecta el número de grupos que obtendremos. Cuanto mayor sea el valor de α, más agrupaciones; cuanto más pequeño es α, menos grupos. Debemos tener en cuenta que el valor de α expresa la fuerza de creer En g₀. Un valor grande indica que la mayoría de las muestras serán distintas y tendrán valores concentrados en G₀. La G es una distribución aleatoria sobre el espacio de parámetros Θ muestreado del DP que asigna probabilidades a los parámetros. El θ_i es un vector de parámetros que se extrae de la distribución G y contiene los parámetros del grupo, la distribución F se parametriza por by_i y x_i es el punto de datos generado por la Distribución Generativa F.

Es importante tener en cuenta que el θ_i son elementos del espacio de parámetros Θ y "configuran" nuestros clústeres. También se pueden ver como variables latentes en x_i que nos dicen de qué componente / cluster la x_i proviene y cuáles son los parámetros de este componente. Así por cada x_i que observamos, dibujamos un θ_i de la distribución G. Con cada sorteo, la distribución cambia según las selecciones anteriores. Como vimos en el esquema de urna Blackwell-MacQueen, la distribución G puede integrarse y nuestras futuras selecciones de θ_i depende solo de G₀: . La estimación de los parámetros θi de la fórmula anterior no siempre es factible porque muchas implementaciones (como el proceso del restaurante chino) implican la enumeración a través de aumento exponencial de k componentes. Por lo tanto, se utilizan métodos computacionales aproximados, como el muestreo de Gibbs. Finalmente, debemos tener en cuenta que aunque los grupos k son infinitos, el número de grupos activos es . Así el θ_i repetirá y exhibirá un efecto de agrupamiento.

2. Uso del proceso de restaurante chino para definir un modelo de mezcla infinita

El modelo definido en el segmento anterior es matemáticamente sólido, sin embargo, tiene un gran inconveniente: por cada nueva x_i que observamos, debemos probar un nuevo θ_i teniendo en cuenta los valores anteriores de θ. El problema es que, en muchos casos, el muestreo de estos parámetros puede ser una tarea difícil y computacionalmente costosa.

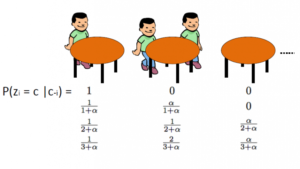
Un enfoque alternativo es utilizar el proceso del restaurante chino para modelar las variables latentes z_i de asignaciones de clúster. De esta manera en lugar de usar θ_i para denotar los parámetros del clúster y las asignaciones del clúster, utilizamos la variable latente z_i para indicar la identificación del clúster y luego usar este valor para asignar los parámetros del clúster. Como resultado, ya no necesitamos muestrear un θ cada vez que obtenemos una nueva observación, sino que obtenemos la asignación del clúster mediante el muestreo de z_i de CRP. Con este esquema, se muestrea un nuevo θ solo cuando necesitamos crear un nuevo clúster. A continuación presentamos el modelo de este enfoque:

Ecuación 2: Modelo de mezcla con PCR

Lo anterior es un modelo generativo que describe cómo los datos x_i y se generan los grupos. Para realizar el análisis de conglomerados debemos usar las observaciones x_i y estimar las asignaciones de clúster z_i.

3. Inferencia del modelo de mezcla y muestreo de Gibbs

Desafortunadamente, dado que los procesos de Dirichlet no son paramétricos, nosotros no se puede usar el algoritmo EM para estimar las variables latentes que almacenan las asignaciones de clúster. Para estimar las tareas usaremos el Muestreo de Gibbs contraído.

El muestreo de Gibbs contraído es un algoritmo simple de Markov Chain Monte Carlo (MCMC). Es rápido y nos permite integrar algunas variables al muestrear otra variable. Sin embargo, este algoritmo requiere que seleccionemos un G₀ que es un conjugado previo de la distribución generativa F para poder resolver analíticamente las ecuaciones y poder tomar muestras directamente de .

Los pasos del muestreo de Gibbs contraído que usaremos para estimar las asignaciones de clúster son los siguientes:

• Inicializa la z_i asignaciones de clúster al azar
• Repita hasta la convergencia
• Seleccionar hacha al azar_i
  
• Mantener el otro z_j arreglado para cada j ≠ i:
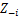
• Asignar un nuevo valor en z_i calculando la "probabilidad de PCR" que depende de z_j y x_j de todos j ≠ i:

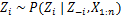
En el próximo artículo, nos centraremos en cómo realizar análisis de conglomerados mediante el uso de modelos Dirichlet Process Mixture. Definiremos dos modelos diferentes de mezcla de proceso de Dirichlet que utilizan el proceso de restaurante chino y el muestreo de Gibbs contraído para realizar la agrupación en conjuntos de datos y documentos continuos.